系列文章目录
本科毕设正在做多轴机械臂相关的内容,这里是一个学习机械臂运动学课程的相关记录。
如有任何问题,可发邮件至layraliu@foxmail.com问询。
1. 数学基础
2. 机械臂几何法与DH表示法
文章目录
- 系列文章目录
- 一、手臂几何法
- 1.机械手臂
- 2.机械手臂描述手臂状态方法
- 3.手臂几何描述方式
- 4.杆件上建立frames
- 5.杆件上建立link transformations
- 5.example:A Manipulator
- 二、actuator,joint,and cartesian spaces(驱动,关节,笛卡尔坐标系)
- 三、DH表达法
- 1.craig
- 2.standard
- 总结
一、手臂几何法
1.机械手臂
多个杆件link相串联;
link间可以相对移动/转动;
2.机械手臂描述手臂状态方法
找出link间的相对几何状态;
在各个link上建立frame,以frame的状态来代表link的状态
3.手臂几何描述方式
joint:关节(先定义每个joint对某一特定的axis进行转动/移动)
link:连接joints的杆件,为刚体
link0:地杆(不动)
link1:和link0相连接,第一个可动的杆件;
link2:第二个可动的;
…
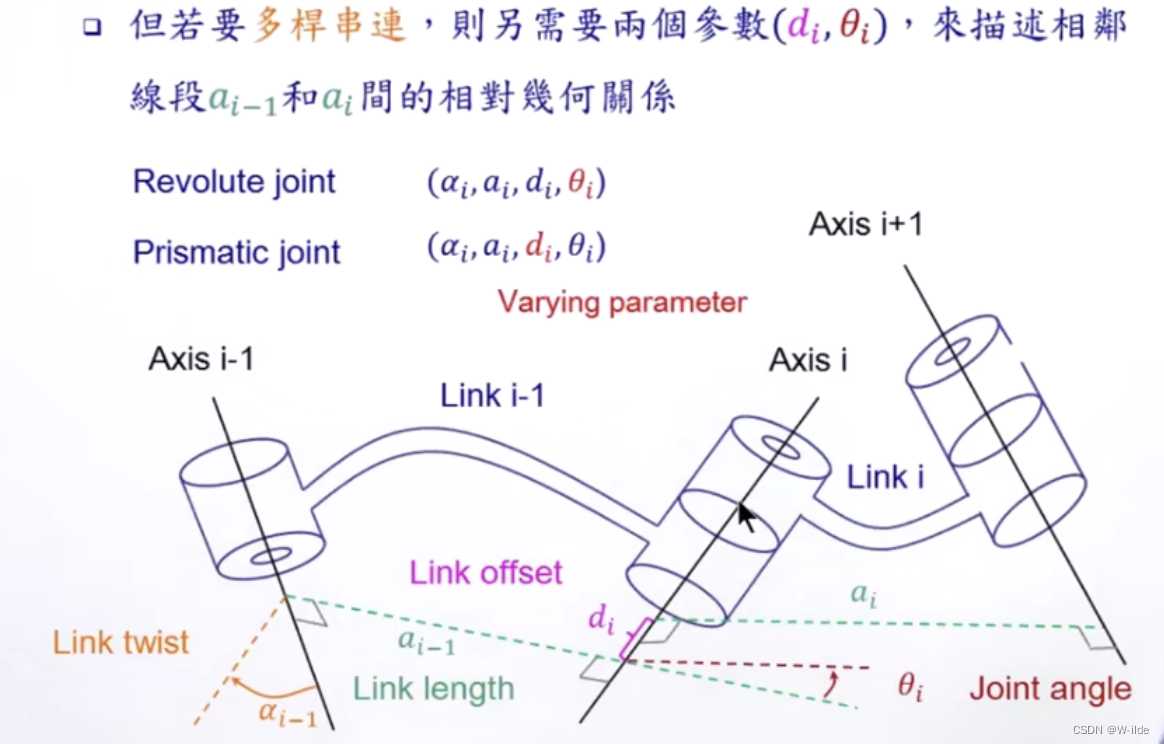
link twist:连杆转角,一个关节的轴相对于另一个关节的轴绕它们的公共法线旋转的角度;
link length:连杆长度,两个关节的轴(旋转关节的旋转轴,平移关节的平移轴)之间的公共法线长度;
link offset:连杆偏距,一个关节与下一个关节的公共法线和它与上一个关节的公共法线沿这个关节轴的距离;(看有没有上下错开)
joint angle:关节角,一个关节与下一个关节的公共法线和它与上一个关节的公共法线绕这个关节轴的转角;
revolute joint:转动,只变动theta这一个参数;
prismatic joint:移动:只变动d这一个参数。
4.杆件上建立frames
zi:转轴或移动axis的方向;
xi:垂直于两个转轴的公垂线(沿着ai方向);
yi:与xi和zi两者垂直,依循右手定则(大拇指指向z,食指指向x,中指指向y)
z=x叉乘y(两个垂直)

对于地杆link0:
实际上:frame 0 coincides with frame 1,即为link length,连杆长度a0=0。
对于revolute joint ,当初始未旋转时,d1=0。
对于prismatic joint,当初始未移动时,θ1=0。(定义两者没有角度差,从空间上)
对于最后一根杆linkn:
实际上:frame n coincides with frame n-1,即为link length,连杆长度an=0。
对于revolute joint ,当初始未旋转时,dn=0。
对于prismatic joint,当初始未移动时,θn=0。(定义两者没有角度差,从空间上)
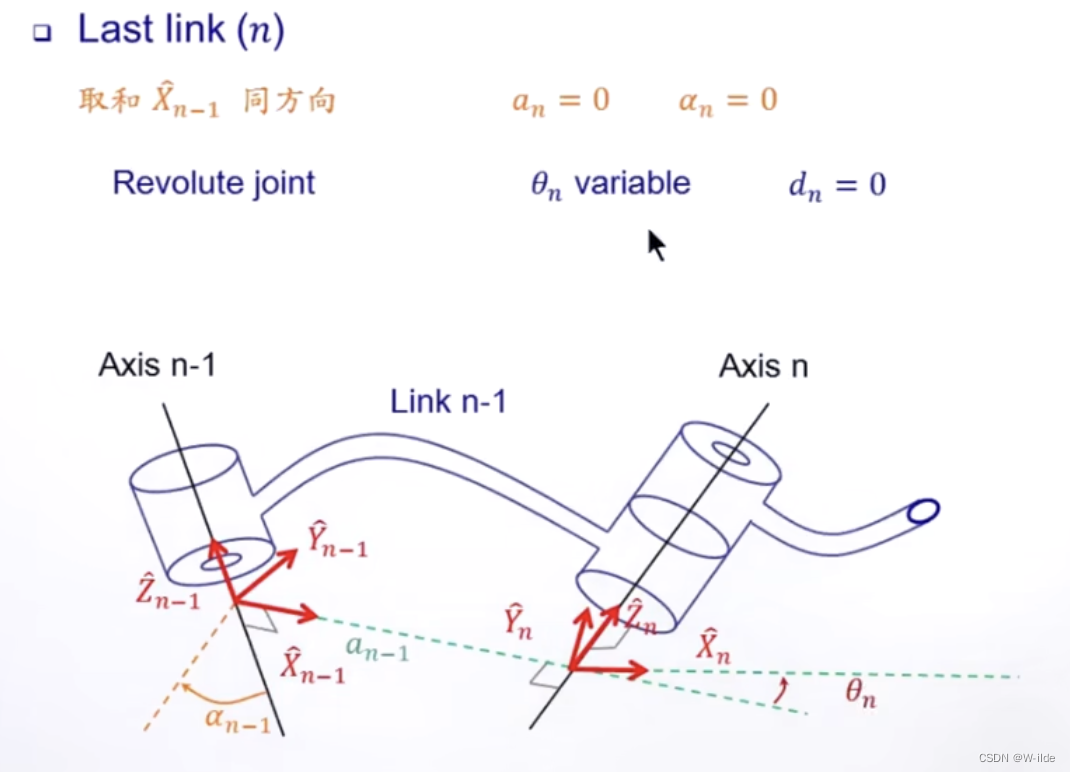
5.杆件上建立link transformations
以下是从frame i 变换到frame i-1
(每次只做一次转动/移动)
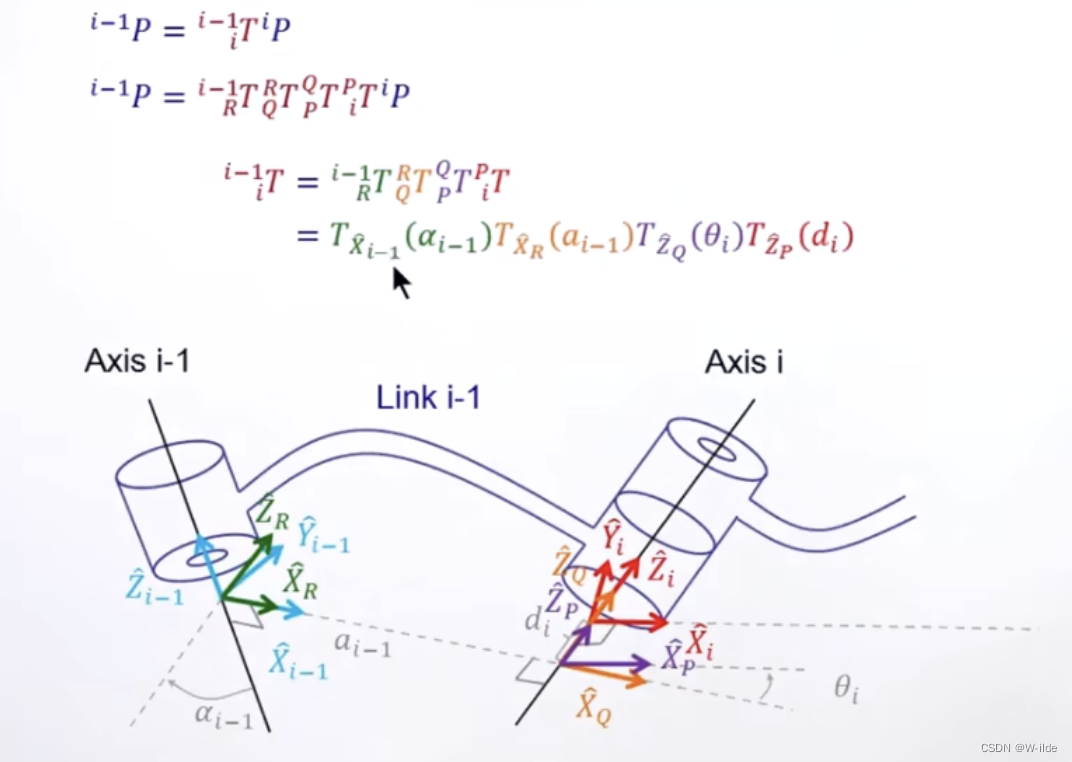
展开:
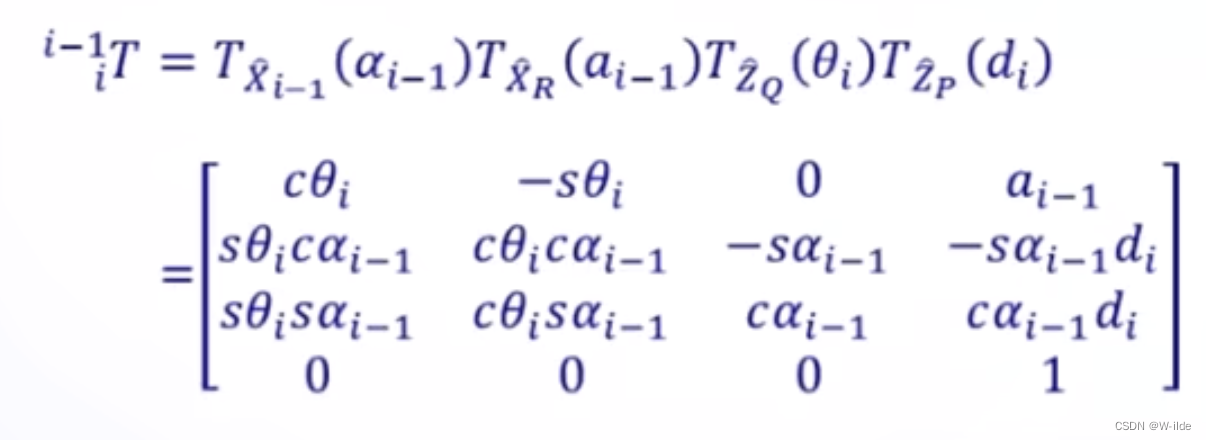
连续link transformations:
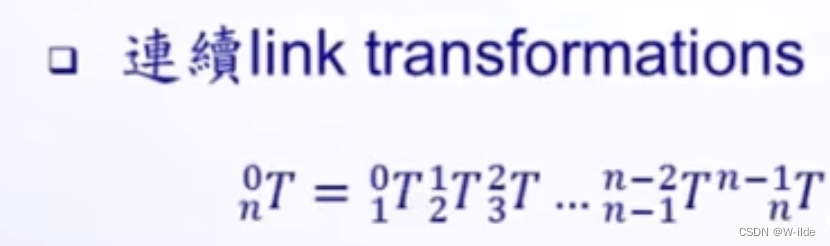
即为在frame n下的向量可转回frame 0来表达。
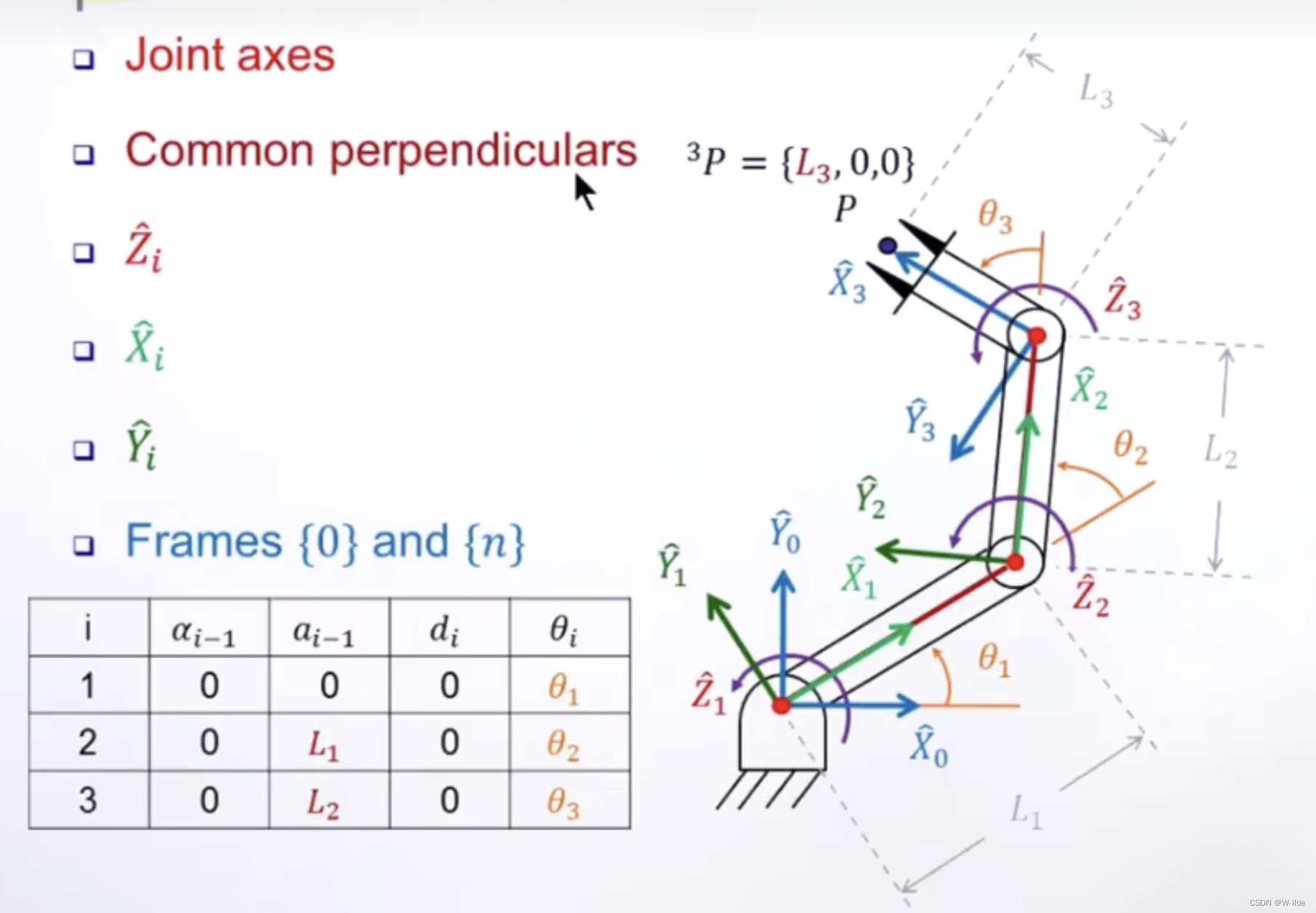
5.example:A Manipulator
eg1:
p点在第三个坐标系下的坐标为(L3,0,0)。
z轴都垂直于纸面朝外侧。
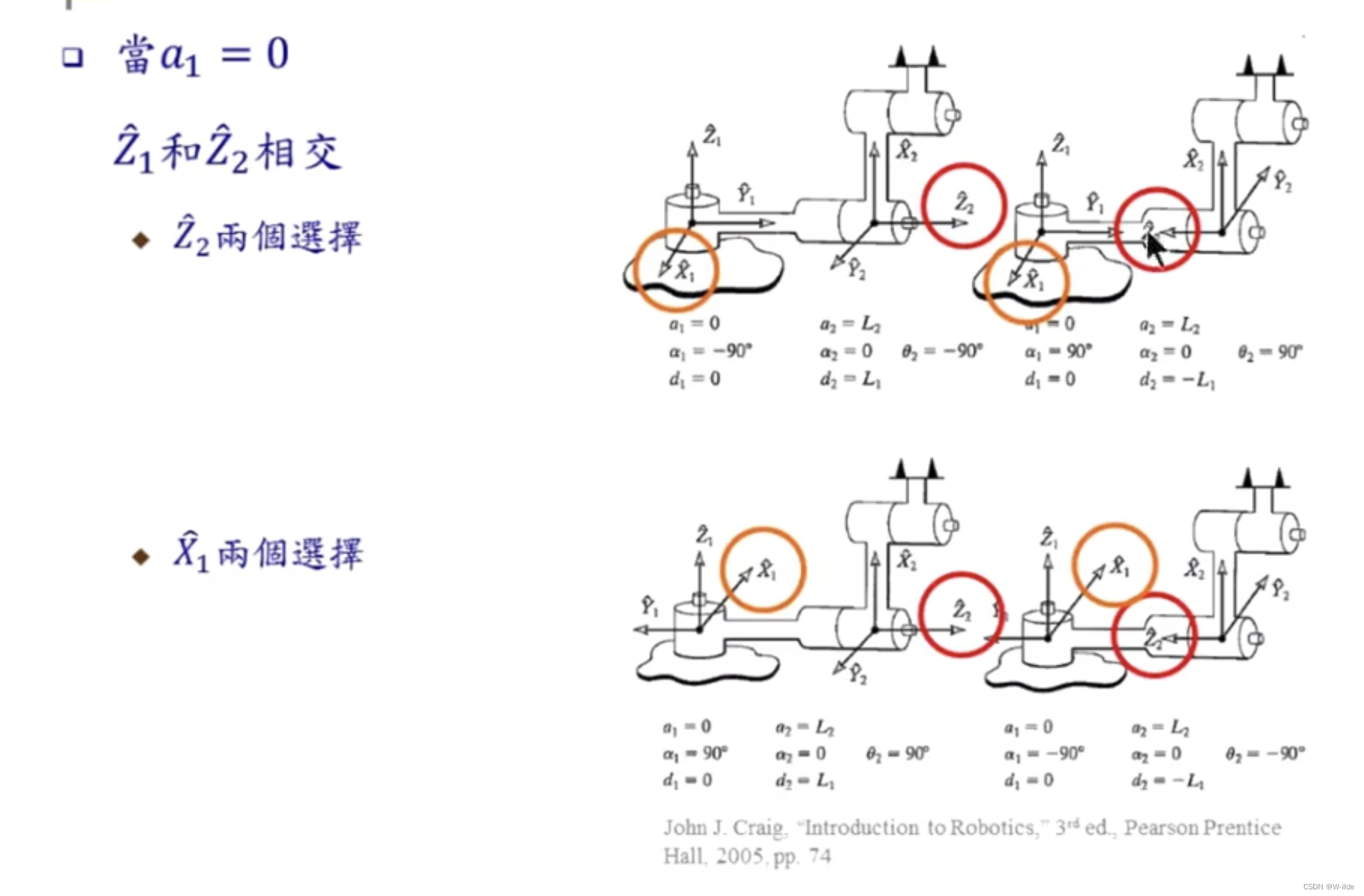
eg2:
link twist是绕zi-1 到zi逆时针方向旋转的角度。

eg3:
eg4:

eg5:

二、actuator,joint,and cartesian spaces(驱动,关节,笛卡尔坐标系)
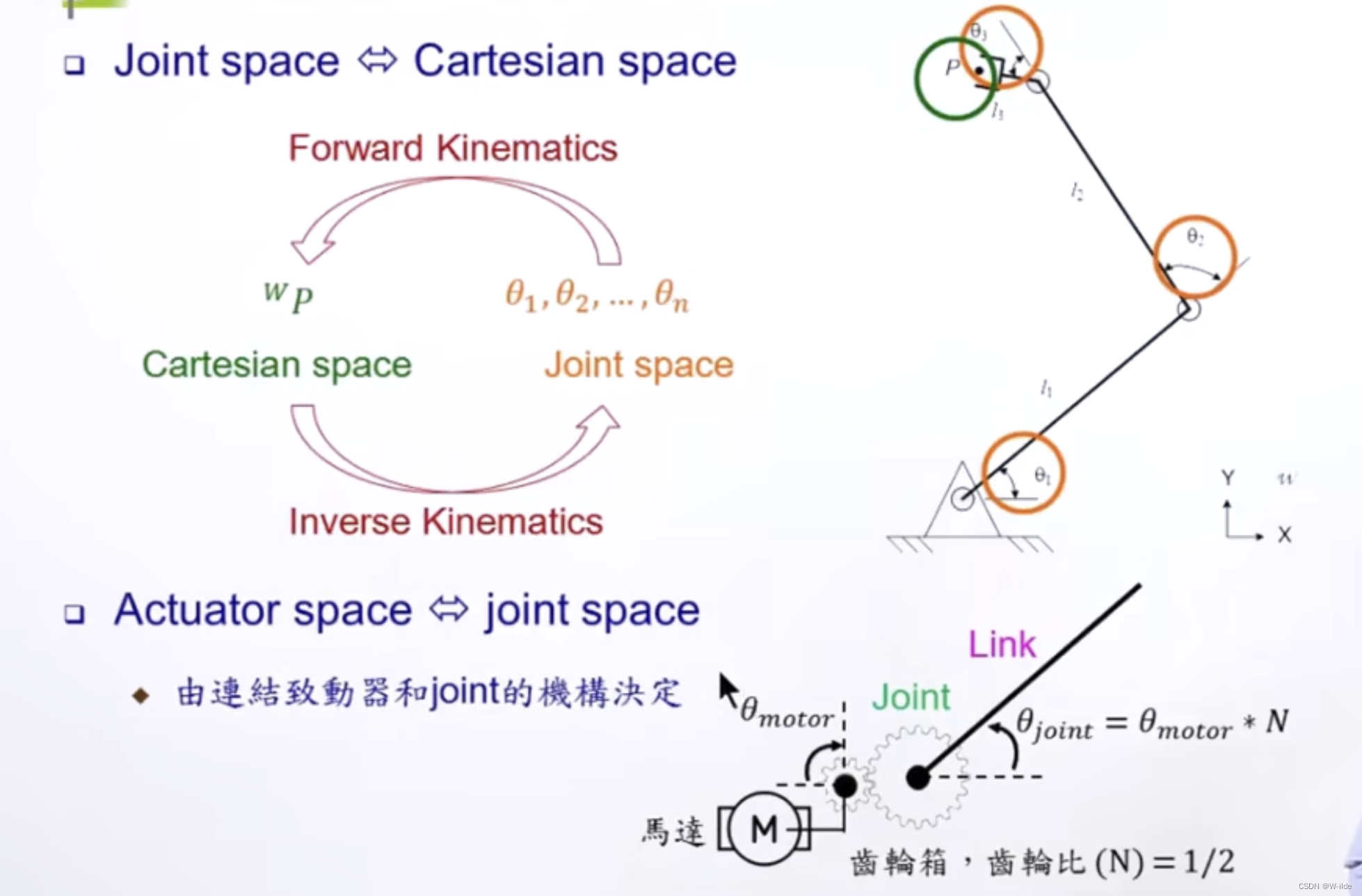
三、DH表达法
1.craig
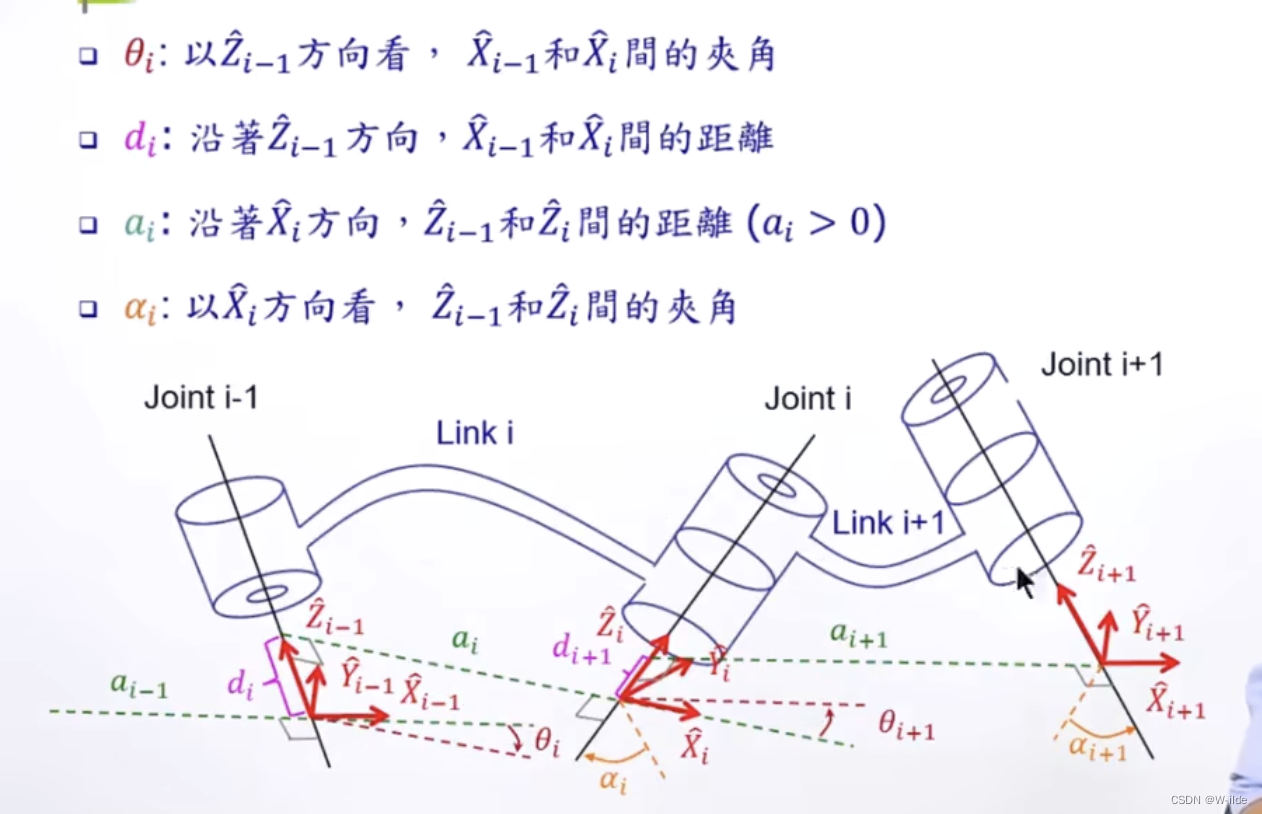

2.standard
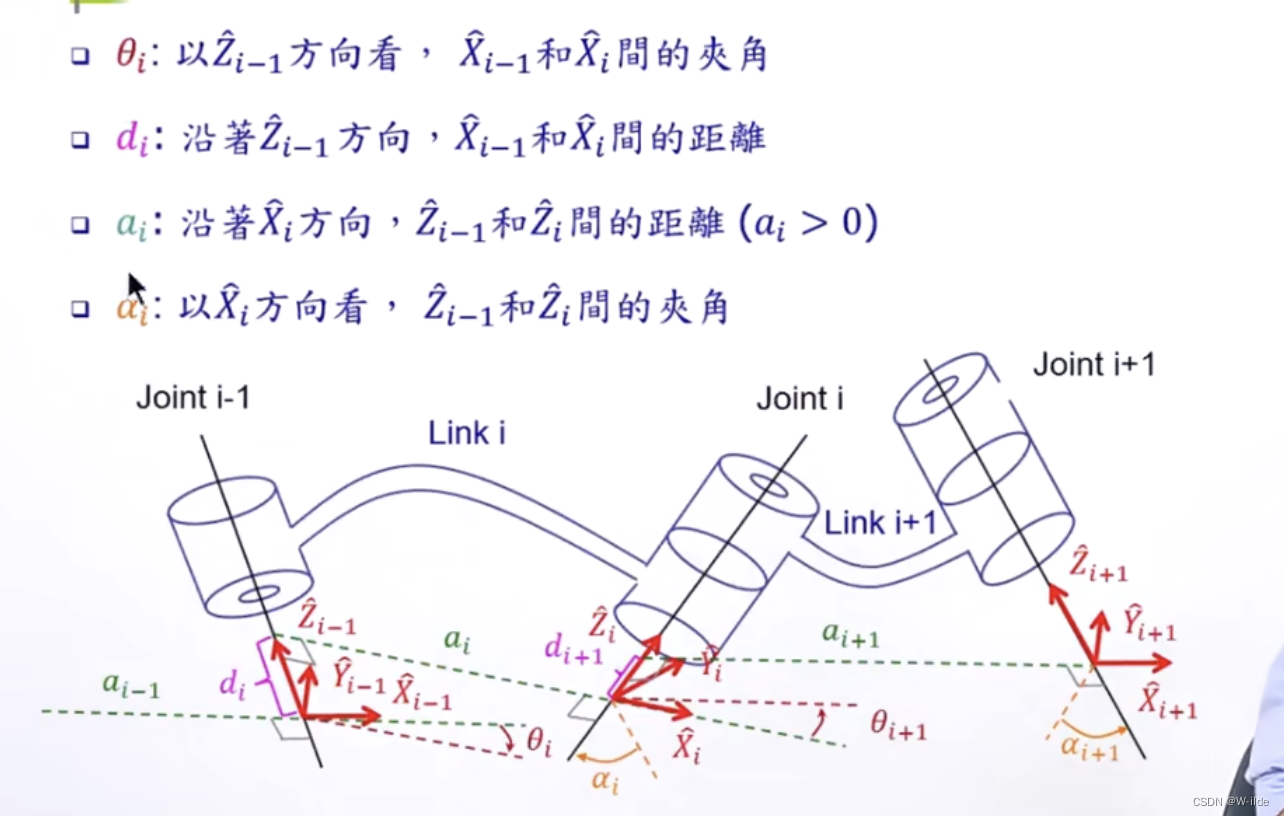

总结
以上就是今天要讲的内容,本文仅仅简单介绍了 多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法的学习记录02——机械臂几何法与DH表示法,而Matlab提供了大量能使我们快速便捷地处理数据的函数和方法。如有任何问题,可发邮件至layraliu@foxmail.com问询。
实现淹没分析)


)











(5-5 Huffuman编码))

)
