小肥柴慢慢手写数据结构（C篇）（5-5 Huffuman编码）

小肥柴慢慢学习数据结构笔记（C篇）（5-5 Huffman编码）

目录
- 5-16 编码案例
- 5-17 Huffman编码原理
- 5-18 Huffman编码/解码实现
- - 5-18-1 大致思路
  - 5-18-2 编码实现
  - 5-18-3 解码实现
  - 5-18-4 测试
- 5-19 实际案例
- 总结
- 参考文献

字符	二进制编码
A	0
B	1
C	10
D	11

字符	二进制编码
A	00
B	01
C	10
D	11

还是使用开篇的问题来介绍Huffman编码：给定A、B、C、D四个字母组成的字符串（ABAACDC），要求使用数字0、1对其进行二进制编码。
step1：首先统计各个字符出现的次数，并作为节点，各字符节点拥有一个权重（weight）来表示字符串中该字符出现的次数。
step2：（每次）挑选weight最小的两个节点进行合并，即为这两个节点生成一个父节点，且父节点的weight为两个子节点weight之和。
step3：从剩下的节点（包含还未合并的原始字符节点和生成的父节点）循环执行上述操作，不断地合并最小的两个节点，最终只剩下一个根节点为止。

具体过程如下图所示：
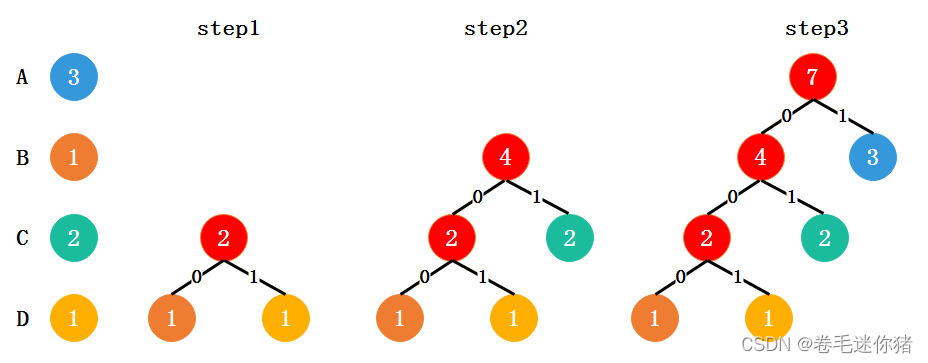
在这里插入图片描述

最后得到编码表：

字符	二进制编码
A	1
B	000
C	001
D	01

编码结果：100011001000001

【观察/性质】

标记所有左枝路径为0，所有右枝路径为1，则可以得到如下编码，称为Huffman编码
按照Huffman编码规则得到的编码结果，一定是在不出现歧义的条件下输出的码长度最短的编码。 ⇒ 后续给出相关学习链接
有关Huffman编码的唯一性，可以绕开数学推导直观地给出证明：
因为所有的叶子结点都是被编码的字符，对树形数据结构来讲，从根节点出发（编码）到叶节点的路径是唯一的，不是吗？ ⇒ 与本章第一节介绍树的基础术语那节对上了！
Huffman编码不是唯一的，因为每次被选中的两个作业节点，总有两种排列方式（且互为镜像）形成新的父节点。
而出现频次高（weight大）的叶子结点排在后面被合并，相反出现频次低（weight小）的叶子结点排在前面被合并，自然而然使得出现频次高的字符的Huffman编码端，从而使得整体编码长度缩短。

关于带权路径长度，WPL

WPL——Weighted Path Length of Tree，简记为 WPL

（1）WPL表示树的所有叶结点的带权路径长度之和。

（2）WPL可用于衡量一颗带权二叉树的优劣。

（3）具体公式为： $WPL=\sum_{i=0}^{ N}w_ip_i$ ，其中 $w_i$ 为权重 $p_i$ 为路径长度，以案例说明
字符A，权重=3，路径长=1；字符B，权重=1，路径长=2…
WPL = 31 + 13 + 22 + 13 = 13
这也是考研/面试/考试经常问到的没有营养的问题。

（4）简单观察这个公式，明显可以看到若能让权重大的字符对应的路径短，则可以减小WPL的值，这与Huffman编码的设计思路是一致的

平均码长于WPL的关系

$L=L(C)=\sum_{i=0}^{ N}p_il_i$ ，其中 $l_i$ 为编码长度， $p_i$ 为编号为 $i$ 的码出现的概率

（1）编码长度 $l_i$ 正好对应WPL中的路径长度（path）

（2）编号为 $i$ 的码出现的概率： $p_i=\frac{w_i}{\sum_{i=0}^{N}w_i}$ ，和WPL中的权重对应起来

（3）其实这个公式本质和WPL一致，仅在定义和变量的命名方式上不同 ⇒ 请看（2）中的定义，秒懂。

至于WPL相关的数学讨论，偏向通信方向和密码学方向（已经超出多数学习数据结构与算法的普通同学的理解了，咱们先挖个坑，有机会慢慢补齐），参考链接 [1]、[2]。

5-18 Huffman编码/解码实现

5-18-1 大致思路

接下来我们会模仿原理部分介绍的Huffman编码/解码操作步骤，尽量降低理解难度。大致思路如下：

（1）编码

step1 统计字符权重
step2 构建Huffman树
step3 对照Huffman树进行编码

需要注意的点：
（1）考虑到编解码的对象是文本字符，可以实用char对应的ASII码作为存储编码列表的索引（index~i），减轻另外实现一套映射算法的额外工作。
（2）为了构建Huffman树（buildHuffTree），用节点数组模拟“森林”（pNode forest[ ]，对应操作addToForest），然后不断从森林中挑选权重最小的两个节点/子树进行合并（getMinNode，mergeNode），在实际挑选时采用每次挑选最小的一个并标记，连续挑选两次的策略，感觉还有改进的空间。
（3）使用递归函数genHuffCode来生成Huffman编码表，借用strcpy和strcat两个API拼接编码字符串。
（4）在判断当前节点是否为字符节点时，可以不做标记，直接判定是否为叶结点即可（isLeaf）。
（5）打印Huffman编码表，采用中序遍历递归实现（printHuffTreeCode）。

（2）解码

step1 拿到之前编码得到的Huffman树
step2 遍历传入的待解码数据（char* / char[]），对照Huffman树找到叶节点，得到一段数据的解码结果，并重置游标（curNode）为Huffman树根节点，循环往复，直到所有数据使用完毕。

5-18-2 编码实现

（1）头文件 HuffmanTree.h

#ifndef _Huffman_Tree_H
#define _Huffman_Tree_H#define LIST_SIZE 256  					//数据列表长度 
#define FOREST_SIZE (LIST_SIZE * 2 - 1) //构建Huffman树需要产生的森林长度
#define CODE_MAX 512                    //每个字符Huffman编码长度 
#define TEXT_MAX 4028                   //解码文本长度 struct TreeNode {char val;int weight;char code[CODE_MAX];struct TreeNode* left;struct TreeNode* right;
};
typedef struct TreeNode* pNode;char* Encode(char *orgData, int orgLen, pNode root);    //编码，返回编码结果 
char* Decode(char *codeData, int codeLen, pNode root);  //解码，返回解码结果 
void releaseTree(pNode root);                           //递归释放节点 
#endif

（2）编码部分
核心代码

char* Encode(char *orgData, int orgLen, pNode root){if(orgData == NULL || orgLen == 0){printf("编码入参错误!\n");return NULL;}if(orgLen == 1){printf("仅有一个字符，不用编码!\n");return NULL;}int i;printf("输入数据：%s\n", orgData);//(1)统计权重 int freq[LIST_SIZE];memset(freq, 0, sizeof(int) * LIST_SIZE);for(i=0; i<orgLen; i++){freq[orgData[i]]++;}//(2)构建Huffman树//C的传参比较繁琐，我不想为了代码看起来漂亮，给buildHuffTree再添加一个引用参数//所以采用了类似深拷贝的做法 pNode tmpTree = buildHuffTree(freq, LIST_SIZE);root->val = tmpTree->val;root->weight = tmpTree->weight;root->left = tmpTree->left;root->right = tmpTree->right;free(tmpTree);printf("\n字符的霍夫曼编码信息如下：\n");printHuffTreeCode(root); //(3)得到编码结果 char* ret = doEncode(orgData, orgLen, root);return ret;
}

干活函数

=========================================

static pNode buildHuffTree(int freq[], int codeListlen){pNode forest[FOREST_SIZE] = {NULL};pNode root = NULL;int i;for(i=0; i<codeListlen; i++){if(freq[i]>0)addToForest(forest, FOREST_SIZE, creatLeafNode(i, freq[i]));}while(1){pNode left = getMinNode(forest, FOREST_SIZE);pNode right = getMinNode(forest, FOREST_SIZE);if(right == NULL) {//仅有一个节点，合并结束 root = left;break; } else {pNode pathNode = mergeNode(left->weight + right->weight);pathNode->left = left;pathNode->right = right;addToForest(forest, FOREST_SIZE, pathNode);}}genHuffCode(root);return root;
}

static void addToForest(pNode forest[], int size, pNode node){int i;for(i=0; i<size; i++){if(forest[i] == NULL){forest[i] = node;break;}}
}

static pNode creatLeafNode(int val, int weight){pNode node = (pNode)malloc(sizeof(struct TreeNode));memset(node, 0, sizeof(struct TreeNode));node->val = val;node->weight = weight;return node;
}

static pNode getMinNode(pNode forest[], int size){pNode node = NULL;int min = -1;int i;for(i=0; i<size; i++){if(forest[i] && (min == -1 || forest[min]->weight > forest[i]->weight))min = i;				}if(min != -1){node = forest[min];forest[min] = NULL;}return node;
}

static pNode mergeNode(int weight){pNode node = (pNode)malloc(sizeof(struct TreeNode));memset(node, 0, sizeof(struct TreeNode));node->weight = weight;return node;
}

static void genHuffCode(pNode curNode){if(curNode){if(curNode->left){strcpy(curNode->left->code, curNode->code);strcat(curNode->left->code, "0");genHuffCode(curNode->left);}if(curNode->right){strcpy(curNode->right->code, curNode->code);strcat(curNode->right->code, "1");genHuffCode(curNode->right);}}
}

=============================================================

static int isLeaf(pNode node){return node->left == NULL && node->right == NULL;
}static void inOrder(pNode curNode){if(curNode){inOrder(curNode->left);if(isLeaf(curNode))printf("字符:%c  权重:%d   编码:%s \n", curNode->val, curNode->weight, curNode->code);inOrder(curNode->right);}
}static void printHuffTreeCode(pNode node){inOrder(node);
}

====================================================

static void transHuffTable(pNode HuffTable[], pNode curNode){if(curNode){if(isLeaf(curNode))HuffTable[curNode->val] = curNode;transHuffTable(HuffTable, curNode->left);transHuffTable(HuffTable, curNode->right);}
}static char* doEncode(char *orgData, int orgLen, const pNode root){pNode HuffTable[LIST_SIZE] = {NULL};transHuffTable(HuffTable, root);//这里写的不好，为了节省空间采取了一个笨办法 int i;int totalSize = 0;for(i=0; i<orgLen; i++)totalSize += strlen(HuffTable[orgData[i]]->code);printf("\n霍夫曼编码长度:%d", totalSize);char* HuffCode = (char *)malloc(sizeof(char) * (totalSize+1));memset(HuffCode, 0, totalSize+1);for(i=0; i<orgLen; i++)strcat(HuffCode, HuffTable[orgData[i]]->code);return HuffCode;
}

5-18-3 解码实现

char* Decode(char *codeData, int codeLen, pNode root){if(codeData == NULL || codeLen == 0 || root == NULL){printf("\n解码入参错误!\n");return NULL;}if(codeLen == 1){printf("仅有一个字符，不用解码!\n");return NULL;}//此处也是一个笨办法，应该去看论文估计一下长度 char* text = (char *)malloc(sizeof(char) * (TEXT_MAX));memset(text, 0, TEXT_MAX);int i,j;pNode curNode = root;//按照之前思路模拟实现，虽然贴近人的自然思维，但是效率不高 for(i=0, j=0; i<codeLen; i++){curNode = codeData[i] == '0' ? curNode->left : curNode->right;if(isLeaf(curNode)){text[j++] = curNode->val;curNode = root;}}return text;
}

=======================================================
完整的 HuffmanTree.c

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "HuffmanTree.h"static pNode getMinNode(pNode forest[], int size){pNode node = NULL;int min = -1;int i;for(i=0; i<size; i++){if(forest[i] && (min == -1 || forest[min]->weight > forest[i]->weight))min = i;				}if(min != -1){node = forest[min];forest[min] = NULL;}return node;
}static pNode mergeNode(int weight){pNode node = (pNode)malloc(sizeof(struct TreeNode));memset(node, 0, sizeof(struct TreeNode));node->weight = weight;return node;
}static pNode creatLeafNode(int val, int weight){pNode node = (pNode)malloc(sizeof(struct TreeNode));memset(node, 0, sizeof(struct TreeNode));node->val = val;node->weight = weight;return node;
}static void addToForest(pNode forest[], int size, pNode node){int i;for(i=0; i<size; i++){if(forest[i] == NULL){forest[i] = node;break;}}
}static void genHuffCode(pNode curNode){if(curNode){if(curNode->left){strcpy(curNode->left->code, curNode->code);strcat(curNode->left->code, "0");genHuffCode(curNode->left);}if(curNode->right){strcpy(curNode->right->code, curNode->code);strcat(curNode->right->code, "1");genHuffCode(curNode->right);}}
}static pNode buildHuffTree(int freq[], int codeListlen){pNode forest[FOREST_SIZE] = {NULL};pNode root = NULL;int i;for(i=0; i<codeListlen; i++){if(freq[i]>0)addToForest(forest, FOREST_SIZE, creatLeafNode(i, freq[i]));}while(1){pNode left = getMinNode(forest, FOREST_SIZE);pNode right = getMinNode(forest, FOREST_SIZE);if(right == NULL) {//仅有一个节点，合并结束 root = left;break; } else {pNode pathNode = mergeNode(left->weight + right->weight);pathNode->left = left;pathNode->right = right;addToForest(forest, FOREST_SIZE, pathNode);}}genHuffCode(root);return root;
}static int isLeaf(pNode node){return node->left == NULL && node->right == NULL;
}static void inOrder(pNode curNode){if(curNode){inOrder(curNode->left);if(isLeaf(curNode))printf("字符:%c  权重:%d   编码:%s \n", curNode->val, curNode->weight, curNode->code);inOrder(curNode->right);}
}static void printHuffTreeCode(pNode node){inOrder(node);
}static void transHuffTable(pNode HuffTable[], pNode curNode){if(curNode){if(isLeaf(curNode))HuffTable[curNode->val] = curNode;transHuffTable(HuffTable, curNode->left);transHuffTable(HuffTable, curNode->right);}
}static char* doEncode(char *orgData, int orgLen, const pNode root){pNode HuffTable[LIST_SIZE] = {NULL};transHuffTable(HuffTable, root);//这里写的不好，为了节省空间采取了一个笨办法 int i;int totalSize = 0;for(i=0; i<orgLen; i++)totalSize += strlen(HuffTable[orgData[i]]->code);printf("\n霍夫曼编码长度:%d", totalSize);char* HuffCode = (char *)malloc(sizeof(char) * (totalSize+1));memset(HuffCode, 0, totalSize+1);for(i=0; i<orgLen; i++)strcat(HuffCode, HuffTable[orgData[i]]->code);return HuffCode;
}static void doReleaseTree(pNode curNode){if(curNode){doReleaseTree(curNode->left);doReleaseTree(curNode->right);}
}char* Encode(char *orgData, int orgLen, pNode root){if(orgData == NULL || orgLen == 0){printf("编码入参错误!\n");return NULL;}if(orgLen == 1){printf("仅有一个字符，不用编码!\n");return NULL;}int i;printf("输入数据：%s\n", orgData);//(1)统计权重 int freq[LIST_SIZE];memset(freq, 0, sizeof(int) * LIST_SIZE);for(i=0; i<orgLen; i++){freq[orgData[i]]++;}//(2)构建Huffman树//C的传参比较繁琐，我不想为了代码看起来漂亮，给buildHuffTree再添加一个引用参数//所以采用了类似深拷贝的做法 pNode tmpTree = buildHuffTree(freq, LIST_SIZE);root->val = tmpTree->val;root->weight = tmpTree->weight;root->left = tmpTree->left;root->right = tmpTree->right;free(tmpTree);printf("\n字符的霍夫曼编码信息如下：\n");printHuffTreeCode(root); //(3)得到编码结果 char* ret = doEncode(orgData, orgLen, root);return ret;
}char* Decode(char *codeData, int codeLen, pNode root){if(codeData == NULL || codeLen == 0 || root == NULL){printf("\n解码入参错误!\n");return NULL;}if(codeLen == 1){printf("仅有一个字符，不用解码!\n");return NULL;}//此处也是一个笨办法，应该去看论文估计一下长度 char* text = (char *)malloc(sizeof(char) * (TEXT_MAX));memset(text, 0, TEXT_MAX);int i,j;pNode curNode = root;//按照之前思路模拟实现，虽然贴近人的自然思维，但是效率不高 for(i=0, j=0; i<codeLen; i++){curNode = codeData[i] == '0' ? curNode->left : curNode->right;if(isLeaf(curNode)){text[j++] = curNode->val;curNode = root;}}return text;
}void releaseTree(pNode root){doReleaseTree(root);
}

5-18-4 测试

（1）测试代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "HuffmanTree.h"int main(int argc, char *argv[]) {char test1[] = {'A', 'B', 'A', 'A', 'C', 'D', 'C'}; //ABAACDCstruct TreeNode huffTree1;char* huffEncode1 = Encode(test1, strlen(test1), &huffTree1);printf("\n\n霍夫曼编码结果: %s", huffEncode1);char* huffDecode1 = Decode(huffEncode1, strlen(huffEncode1), &huffTree1);printf("\n\n霍夫曼译码结果: %s", huffDecode1);printf("\n=======================================\n");//write file namechar test2[] = {'w', 'r', 'i', 't', 'e', ' ', 'f', 'i', 'l', 'e', ' ', 'n', 'a', 'm', 'e'}; struct TreeNode huffTree2;char* huffEncode2 = Encode(test2, strlen(test2), &huffTree2);printf("\n\n霍夫曼编码结果: %s", huffEncode2);char* huffDecode2 = Decode(huffEncode2, strlen(huffEncode2), &huffTree2); printf("\n\n霍夫曼译码结果: %s", huffDecode2);printf("\n=======================================\n");return 0;
}

（2）测试结果
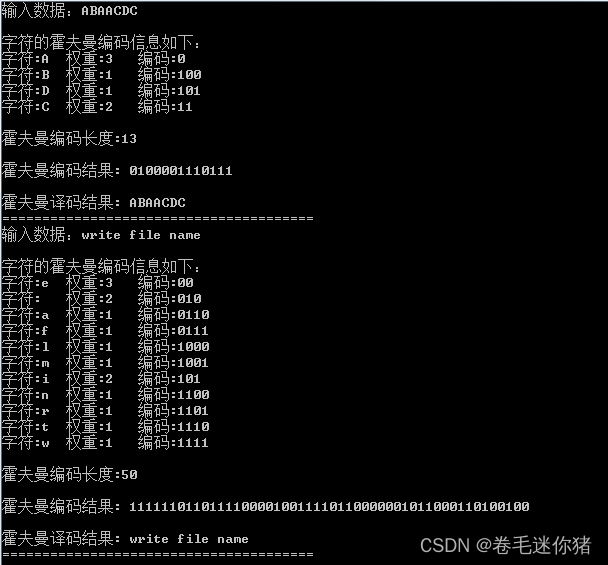
在这里插入图片描述

【遗憾】
（1）正如前面讨论的，这个程序是参考[3]修修补补完成的，当然也可以参考[3]和[4]去做成完整版的利用Huffman编码对文件进行压缩和解压的经典案例（重点在于能让大家观察到压缩/解压的操作的时间和空间效率，真正做到学以致用），
（2）对Huffman编解码的对应数学理论我们仅了解到皮毛，因此在具体编码中还有很多申请/释放空间的处理不够智慧，应该抽空研究一下真实开源案例，看看学习别人的实现手法。
（3）黑皮书里给出了相关论文，见[13]，[14]，[15]，[16]。

以上问题，有空我们补一个帖子试试看。

【注】另外，很多Huffman教学贴中，编码实现阶段，为节点定义了一个指向父节点的指针，也不失为一种常见的解决方案，参看[4]

// 定义哈夫曼树节点
typedef struct {int weight;int parent;int l_child;int r_child;char data;
} HTNode, * HuffmanTree;
typedef char** HuffmanCode;

5-19 实际案例

（1）硬件编解码，参考 [6]，[7]，[8]
（2）其他参考[9]，[10]，[11]，[12]

多媒体方向的水很深，看情况慢慢研究吧。

总结

（1）Huffman编码的应用非常广泛。
（2）Huffman编码是一种变长的编码，可配合类似树状的数据结构存储编码表。
（3）对于森林这个概念，我们没有介绍，直接在实践中学习。

【吐槽】C的传值解决方法不太优雅。

参考文献

[1] 信息与编码系列（一）源码
[2] 信息与编码系列（二）最优码——Huffman码
[3] C语言实现Huffman的编码和解码 ==> 值得看，树形结构的打印不错，对文件的编解码也挺好
[4] C语言课程设计-文件的哈夫曼编码与解码 ==> 对时间和空间的统计展示值得借鉴
[5] 哈夫曼编码详细证明步骤
[6] 硬件huffman解码器（一）：huffman编码原理
[7] 硬件huffman解码器（二）：串行解码及其优化
[8] 硬件huffman解码器（三）-并行解码
[9] 语音处理：霍夫曼编码算法原理分析 ==> 提到了Jpeg
[10] MP3 和 AAC 中huffman解码原理，优化设计与参考代码中实现
[11] Android 性能优化 03—Bitmap优化02（huffman压缩）
[12] Android图片压缩原理分析（三）—— 哈夫曼压缩讲解 ==> Android Skia 图像引擎
[13] D. A. Huffman,“AMethod for the Construction of Minimum Redundancy Codes,” Proceedings of the IRE, 40 (1952),1098-1101. ==> 开山鼻祖
[14] D.E. Knuth, “Dynamic Huffman Coding,”Journal of Algorithms, 6 (1985),163-180.
[15] L.L. Larmore, “Height-Restricted Optimal Binary Trees,”SIAM Journal on Computing, 16 (1987),1115-1123.
[16] L. L. Larmoreand D.S. Hirschberg,“A Fast Algorithm for Optimal Length-Limited Huffman Codes,”Journal of the ACM, 37 (1990), 464-473.