Fiddler是一个强大的网络调试工具，它可以帮助用户捕获HTTP和HTTPS请求和响应，从而进行调试和分析。在Fiddler的用户界面中，工具栏是一个非常重要的组成部分，它提供了许多常用的操作和功能，方便用户进行网络调试。以下是工具栏使用介绍。

一、备注（Comments）

选择一个或多个请求后，点击此图标可以为这些请求添加备注，备注信息会显示在“Comments”列中。

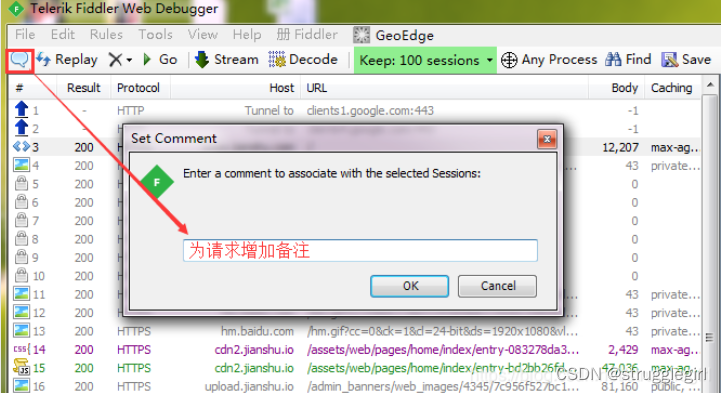
二、回放（Replay）

选择一个或多个请求后，点击此图标可以重新发送这些请求。这对于需要重复发送相同请求的场景非常有用。回放在键盘的快捷键是R键，选择一个会话点击R键可以直接回放该会话（shift+R可设置重放次数达到重放攻击）

三、清除会话（Remove）

提供多种清除会话的选项，例如清除所有会话、清除所有图像类会话、清除所有CONNECT会话等。

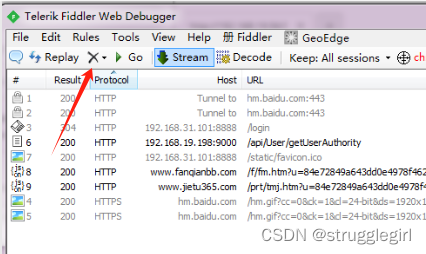
四、调试（Go）

1、调试按钮

当请求在断点处暂停时，点击此按钮可以使请求继续执行。

2、添加断点

在调试时可以添加断点，如下图所示，点击底部状态下图所示位置开始增加断点

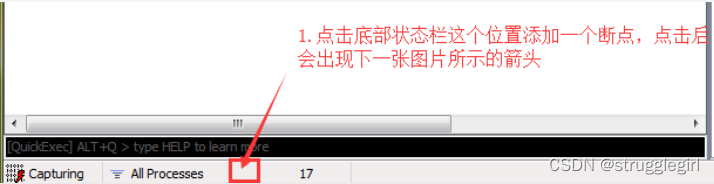
3、发送断点

点击后会显示一个箭头朝上的图标，表示请求发送时会产生一个断点。

4、产生断点

再次点击这个图标会显示一个箭头朝下的图标，表示请求返回时会产生一个断点。

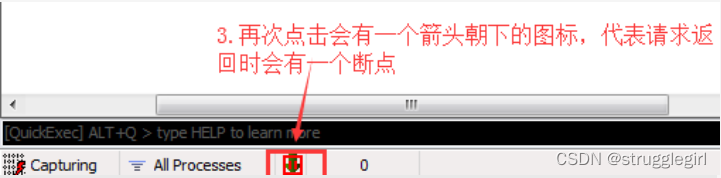
五、流模式和缓冲模式切换

默认是缓冲模式，默认所有的http请求数据都返回给fiddler它才会在控制面板展示出来

六、解码请求

七、保持会话

实际上保存的会话数量越多，fiddler占用的内存越大，根据电脑性能选择保持多少会话，尽量不要all sessions

八、过滤请求

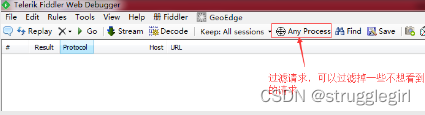
具体操作如下：

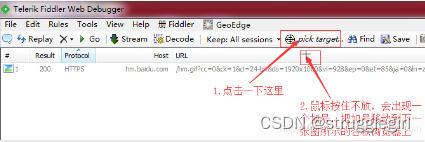
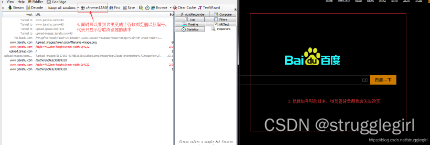
九、查找功能

十、保存会话

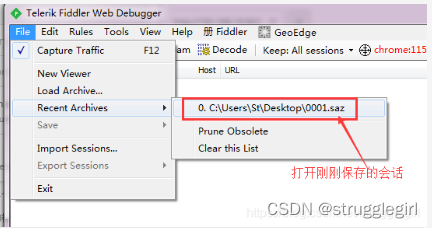
十一、保存截图

十二、计时器

十三、快速启动浏览器

十四、清除ie浏览器缓存

十五、解码和编码

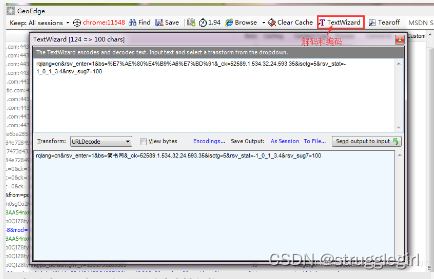
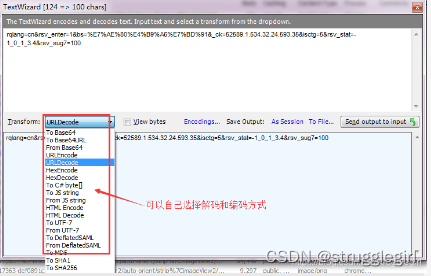
十六、设置右侧面板为浮窗的形式

十七、msdn搜索

具体的工具栏功能和图标可能会因Fiddler的版本或配置而有所不同，因此建议查阅相关文档或官方资源以获取最准确的信息。