心路历程：

这道题是一个动态规划题，但是其实递推关系很难想到，如下图所示：
MDP建模：
状态：以i,j为右下角的正方形
动作候选集：这道题的动作候选集其实是是否选择其左上角邻接的三个位置，动作候选集的特征不是特别明显。
返回值：最大正方形的边长

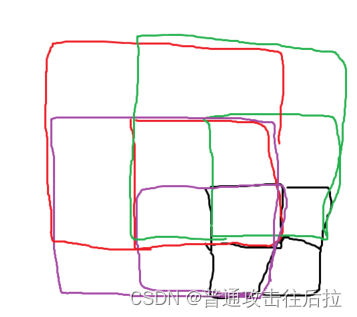
注意的点：

1、注意题目中给出的是’0’而不是0
2、注意边长要转化为面积

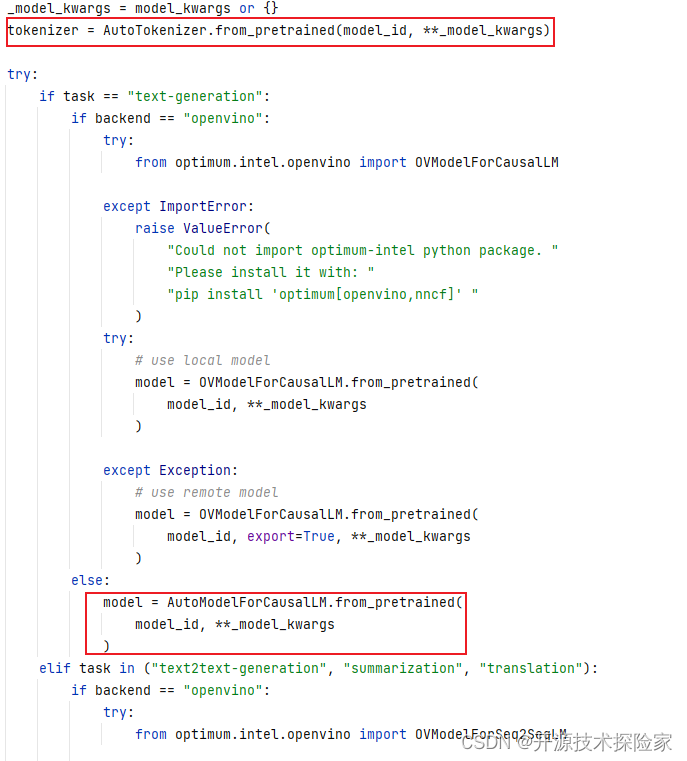
解法：动态规划：

class Solution:def maximalSquare(self, matrix: List[List[str]]) -> int:n, m = len(matrix), len(matrix[0])@cachedef dp(i, j):  # 以i,j为右下顶点的正方形的边长最大值if matrix[i][j] == '0': return 0if not (0 <= i < n) or not (0 <= j < m):  return 0return min(dp(i-1, j-1), dp(i, j-1), dp(i-1, j)) + 1res = 0for i in range(n):for j in range(m):res = max(res, dp(i, j))return res ** 2