日升时奋斗，日落时自省 

目录

1、全排列

2、全排列II

3、子集

4、组合

---

1、全排列

首先要了解全排列是怎么样的

例如:数组[1,2,3]的全排列（全排列就是不同顺序排列方式）

例子所有的排列方式如：[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]六种

画个图来解释一下：

代码：

    List<List<Integer>> result;  //终态 结果List<Integer> path;  //每条路径的结果public List<List<Integer>> permute(int[] nums) {result=new ArrayList<>();path=new ArrayList<>();int n=nums.length;if(n==0){return result;}//标记位boolean[] vis=new boolean[n];//参数  数组 当前层数  数组个数 标记位bfs(nums,0,n,vis);return result;}public void bfs(int[] nums,int index,int len,boolean[] vis){//层数等于数组个数表示路径已经收集齐一次 进行终态添加if(index==len){result.add(new ArrayList<>(path));return ;}//每层都会进行整个数组的遍历for(int i=0;i<len;i++){//但是需要判断标记位 该数字是否被标记使用，这里需要是没有使用过的数字if(!vis[i]){//进来后就算是被使用了， 进行标记一下vis[i]=true;//同时添加到路径中path.add(nums[i]);//进行下一层 遍历bfs(nums,index+1,len,vis);//如果下一层进行失败 当前层的该数也没有用了，因为这条路走不通//标记位删除的标记vis[i]=false;//同时删除当前数位path.remove(path.size()-1);}}}

2、全排列II

题目来源：. - 力扣（LeetCode）

题目的主要目的就是让全排列不要重复，重复的就不要写出来了

首先我们想前后一样就不选了，但是这个是需要一个前置条件的，需要给数组排个序

去重条件就是 nums[i]！=nums[i-1]并且当前位置标记位为false（说明没有选过）为进入条件

条件代码：!check[i]&&nums[i]!=nums[i-1]    （但是这样是不行的）

注：i-1是会越界的

再次修改的条件代码：!check[i]&&(i==0||nums[i]!=nums[i-1])

注：其实还是不完全的，如果同一层的check的上一个（check[i-1]）为true说明选过了，此时nums[i]==nums[i-1]，我们选还是不选，当然是选

其实全排列的规律就是  1(1)2(2)2(3)   1(1)2(3)2(2)   其实这里就相当于我们选了(1)(2)(3) 这种情况

放弃了(1)(3)(2)这种类似情况

注：这里红括号表示层数

方法一：

代码：

    List<List<Integer>> ret;    //终态集List<Integer> path;         //结果集boolean[] check;public List<List<Integer>> permuteUnique(int[] nums) {ret=new ArrayList<>();path=new ArrayList<>();check=new boolean[nums.length]; //标记位Arrays.sort(nums); //排序 为去重做的准备dfs(nums,0);return ret;}public void dfs(int[] nums,int pos){//终态条件if(path.size()==nums.length){ret.add(new ArrayList<>(path));return ;}for(int i=0;i<nums.length;i++){//当前标记位==false  &&   (i不能越界||前后不相等||同层上一个为true)if(!check[i]&&(i==0||nums[i]!=nums[i-1]||check[i-1])){path.add(nums[i]);check[i]=true;dfs(nums,pos+1);path.remove(path.size()-1);check[i]=false;}}}

方法二：

如果觉得上述代码比较难以接受的话的，只要理解全排列就行，这里可以使用其他集合来处理去重问题例如使用Set来去重

    List<List<Integer>> ret;List<Integer> path;boolean[] check;public List<List<Integer>> permuteUnique(int[] nums) {ret=new ArrayList<>();path=new ArrayList<>();check=new boolean[nums.length];Arrays.sort(nums);dfs(nums,0);//创建set集合Set<List<Integer>> set=new HashSet<>();//添加后进行去重for(int i=0;i<ret.size();i++){set.add(ret.get(i));}//清除ret原来的值ret.clear();//重新将去重后的数据进行添加for(List<Integer> tmp:set){ret.add(tmp);}return ret;}public void dfs(int[] nums,int pos){if(path.size()==nums.length){ret.add(new ArrayList<>(path));return ;}for(int i=0;i<nums.length;i++){if(!check[i]){path.add(nums[i]);check[i]=true;dfs(nums,pos+1);path.remove(path.size()-1);check[i]=false;}}}

3、子集

题目来源：LCR 079. 子集 - 力扣（LeetCode）

子集就是我们在数学里理解的意思：

[1,2,3]的子集就是[],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3]

图示：

注：当前层到下一层的位置都会+1

代码：

    List<List<Integer>> ret;   //终态集List<Integer> path;       //结果集（路径集）public List<List<Integer>> subsets(int[] nums) {ret=new ArrayList<>();path=new ArrayList<>();dfs(nums,0);return ret;}private void dfs(int[] nums, int pos) {//子集  是  每次都会进行添加ret.add(new ArrayList<>(path));//当前层的位置 是上层位置+1   pos就是上层位置+1来的for(int i=pos;i<nums.length;i++){path.add(nums[i]);//递推条件就是数组 和 下层的下一个位置dfs(nums,i+1);path.remove(path.size()-1);}}

4、组合

题目来源：77. 组合 - 力扣（LeetCode）

子集的升级版（个人是这么理解的）

给定一个数n和一个组合个数k

n=4 ,k=2

其实就是让我们把[1,2,3,4]进行组合:

结果为：[1,2],[1,3],[1,4],[2,3],[2,4],[3,4] （其实是有点像子集的只是稍微加了点处理）

子集没有限定条件来添加结果集，这里添加了条件是 当结果集为k 的时候添加到终态集中

这里还是拿n=3，k=2再来举一个例子会更清楚些

其实就是让我们把[1,2,3]进行组合:

结果为：[1,2],[1,3],[2,3]

图示：

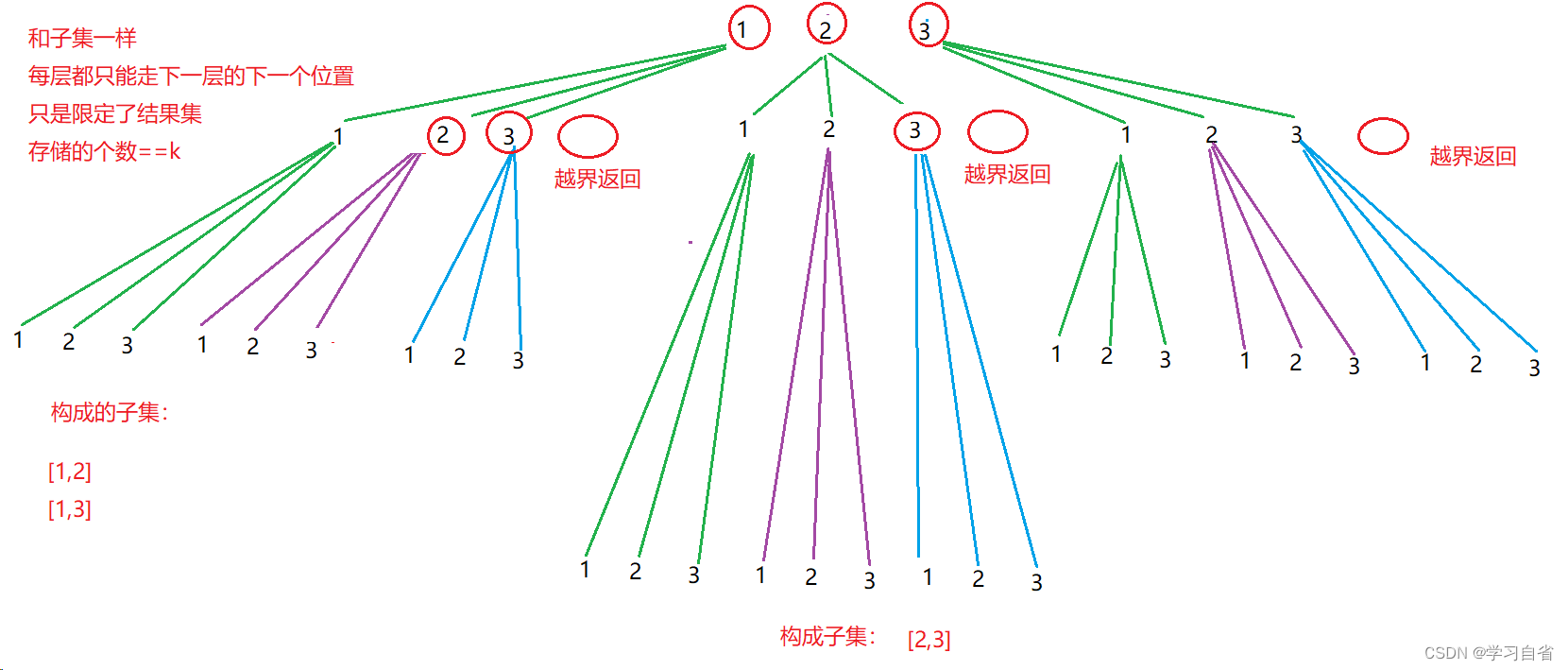
代码：

其实仔细看看也就是只有条件边了，其他都没有改变

    List<List<Integer>> ret;List<Integer> path;int num,key;  //设置为全局变量方便获取，不用通过传参来使用public List<List<Integer>> combine(int n, int k) {ret=new ArrayList<>();path=new ArrayList<>();num=n;key=k;dfs(1);return ret;}public void dfs(int pos){//限定结果集的个数为kif(path.size()==key){ret.add(new ArrayList<>(path));return;}for(int i=pos;i<=num;i++){path.add(i);dfs(i+1);path.remove(path.size()-1);}}

注：如果友友们还是感觉有点陌生我换个方法来看看

    List<List<Integer>> ret;List<Integer> path;int n,key;  //设置为全局变量方便获取，不用通过传参来使用public List<List<Integer>> combine(int[] nums, int k) {ret=new ArrayList<>();path=new ArrayList<>();key=k;dfs(nums,0);return ret;}public void dfs(int[] nums,int pos){//限定结果集的个数为kif(path.size()==key){ret.add(new ArrayList<>(path));return;}for(int i=pos;i<nums.length;i++){path.add(nums[i]);dfs(nums,i+1);path.remove(path.size()-1);}}

注：这个题目是稍微改动了一下，作为例题来看，是不是就和子集很相似，就是变了个条件

总结：知道全排列，子集和组合不一定是为了这几个题，这些方法有时候更像是枚举的形式出现，可以作为地基，稍作改善很多题就在一个小范围内进行解决