文章目录
- 操作系统是什么?
- 1. Linux家族介绍
- 2. Linux的安装方式
- 3. 常用指令
- 3.1 ls [选项] [目录/文件](显示目录或文件信息)
- 3.2 pwd(显示当前所在目录)
- 3.3 任意指令加上 --help(查看指令的用法)
- 3.4 cd 目录名(切换目录)
- 3.5 touch 文件名(创建普通文件)
- 3.6 mkdir 目录名(创建目录)
- 3.7 rmdir 目录名(删除空目录)
- 38. rm -rf 文件或目录
- 3.9 man 指令名
- 3.10cp [-rf] 源文件或目录 目标文件或目录(拷贝)
- 3.11 mv [-f] 源文件或目录 目标文件或目录(剪切)
- 3.12 which(查看指令路径)
- 3.13 tree(以树状结构显示目录)
- Ctrl + c终止任何情况
- 3.14 >(输出重定向)
- 3.1 cat [选项] 文件(查看文件内容)
学习linux的重点不是学习敲linux的命令,重点是学习相关的知识,命令多敲就会了,反而是周边知识是基础、是重点,能提高专业素养。
操作系统是什么?
是一款进行软硬件资源管理的软件,操作系统在计算机中的层次:
- 最底层是硬件,如cpu、内存、硬盘、显示器和键盘等;
- 硬件之上是设备驱动,比如声卡、网卡驱动;
- 设备驱动之上就是操作系统了,比如Windows、linux和macos等;
- 操作系统之上是用户最熟悉的应用软件,比如浏览器、QQ、office等。
1. Linux家族介绍

Linux是一款开源的操作系统,Linux只是一个总称,大体上来讲,Linux分为两个生态体系,redhat和debian。商业版本以redhat为代表,开源社区版本则以debian为代表。
Redhat旗下的发行版本:
- redhat :红帽自家服务器,商用而非免费,主要针对企业市场的商业 Linux 发行版。
- centos :基于红帽重新封装的去掉版权信息的免费版本,专门用于用于企业和服务器。
- fedora :基于红帽社区支持的桌面版,里面的包是红帽的实验版本,相对较新,它在技术上领先,但不长期支持。
Debian旗下的发行版本:
- debian :debian自家纯净系统,一般来说Debian作为适合于服务器的操作系统,它比Ubuntu要稳定得多。
- Ubuntu : 在debian系统上封装了许多工具,Ubuntu有着漂亮的用户界面,但这也决定了它最佳的应用领域是桌面操作系统而非服务器操作系统。
- Kali : Kali Linux 前身是 BackTrack(基于ubuntu),是一个基于 Debian 的 Linux 发行版,包含很多安全和取证方面的相关工具。
- Linux Mint:也是基于 Debian 和 Ubuntu 的,提供了额外的多媒体支持和美化。
也还有其他体系,不过不常见。目前这么多发行版中,CentOS和Ubuntu用的较多。
2. Linux的安装方式
- 双系统:在windwos系统的基础上再装一个linux(不推荐,千万别这么做)。
- 虚拟机:装一个虚拟机软件(vm ware或者virtual box),下载好linux系统文件,在虚拟机软件中安装linux(推荐,有时间可以搞搞,许多人学习过程是这样做的)。
- 云服务器:云服务器esc或者轻量级应用服务器(也称轻量级云服务器),墙裂推荐,比较方便。可以先在阿里云或腾讯云、或华为云等厂商那去试用1或3个月,用于学习没有问题。
最后下载一个xshell,这个是连接服务器的软件,用以下命令连接:ssh root@要连接的服务器公网ip,最后输入密码就可。
我这不提供软件下载链接,大伙自己去找,初学者也可锻炼下自己的检索能力。不过如果有使用虚拟机方式安装的,推荐用vmware,安装后网上或B站找激活码激活就行,linux系统文件推荐在这里下载:itellyou,自己直接搜这个,防止大伙下到魔改版或者盗版。
3. 常用指令
3.1 ls [选项] [目录/文件](显示目录或文件信息)
作用是显示目录下或当前目录下的文件信息,常用选项很多,以下只随便列出几条常用的:
- -a:列出所有文件,包括以.开头的隐藏文件;
- -l:列出文件详细信息;
- -R:递归列出目录下所有文件。
还有很多选项,我就不举例了,这样一堆列下来学起来没意思,大伙自己去搜。
举例:ls -a、ls -l(或ll)、ls -la(ll -a),在当前目录就直接输就行,指定目录的话后面跟上目录的路径,比如ls /test/dir。
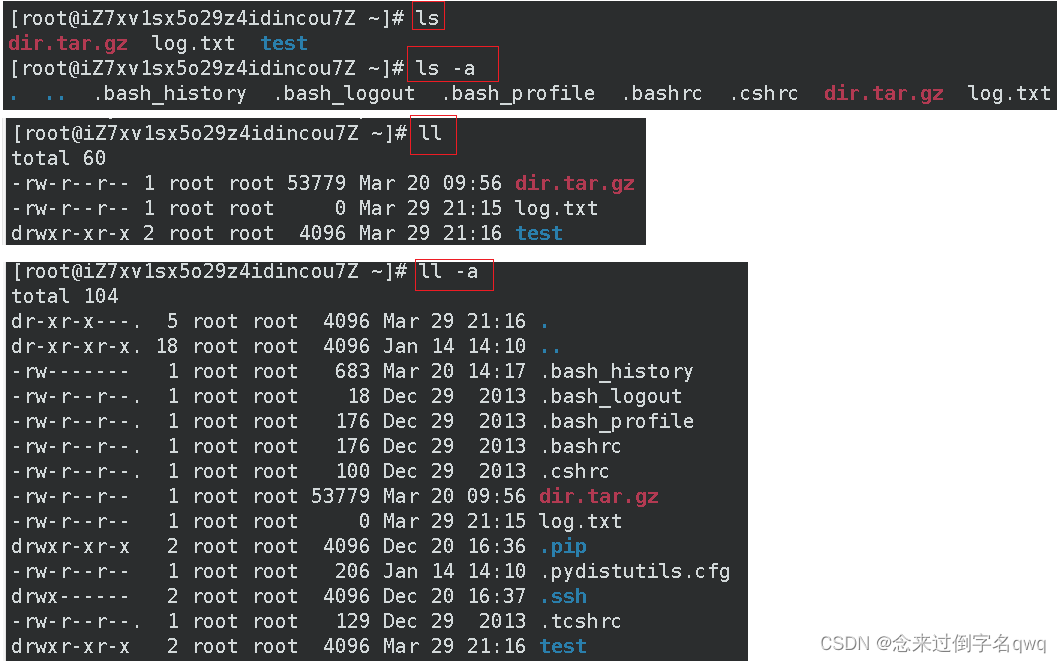
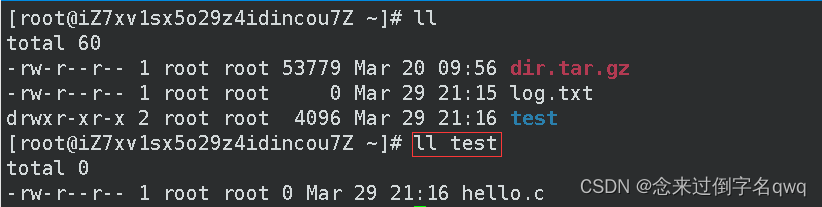
蓝色说明是目录,白色是普通文件。-l选项显示详细信息,这些信息都很重要,以后会有介绍,这里从左往右简单地说下大概都是什么。这些信息表达有文件类型和该文件哪些人有哪些读写权限(不同用户对于该文件可以有不同权限)、该文件的所属者和所属组、文件大小和更新日期等。
3.2 pwd(显示当前所在目录)

~代表用户家目录,顾名思义就是用户目录。而Linux是一个多用户的操作系统(后面介绍创建其它普通用户指令),每个用户都有自己的用户家目录。
/是Linux根目录,根目录下的子目录都有自己的作用,大伙可以自己去搜索下:
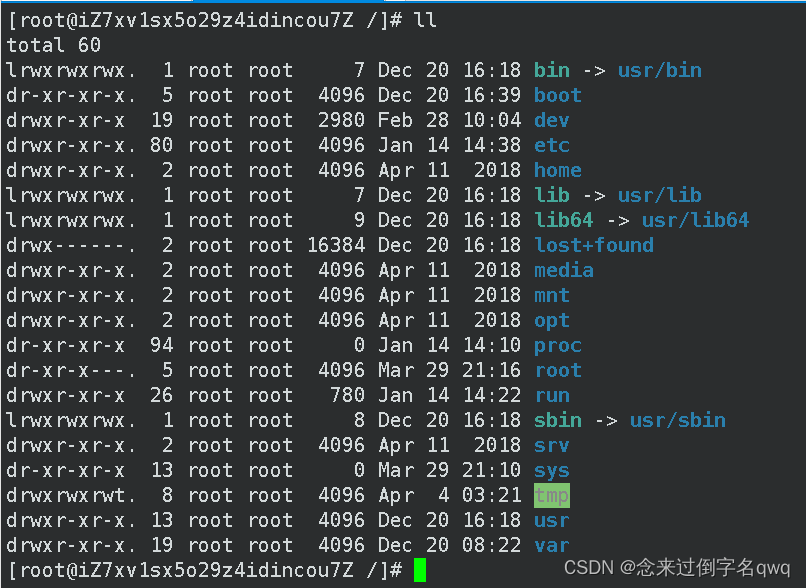
3.3 任意指令加上 --help(查看指令的用法)
有些指令很多选项,这样查看会列出很多,不要惊慌,比如ls --help:
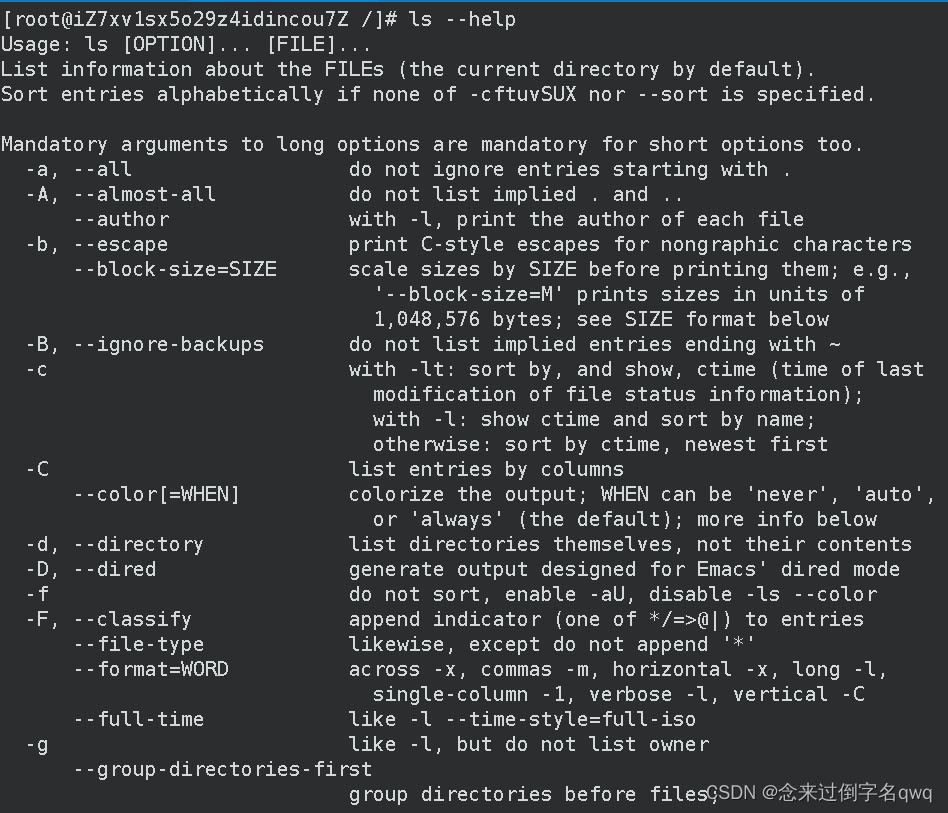
3.4 cd 目录名(切换目录)
常用操作:
-
回到上级目录:cd …(两个点…就代表上级目录,一个点.代表当前目录,其实.和…就是隐藏的文件,可以用ls带上-a选项查看到)

-
使用绝对路径切换目录,只要存在且有权限操作,不管当前在任何目录下,都可以随便切换,比如当前在用户家目录下执行cd /usr切换到根目录下的usr目录:

-
使用相对路径切换目录,相对路径相对的是当前所在目录,这里涉及到前面说的.和…。例如我想要进入到当前目录下的111目录:
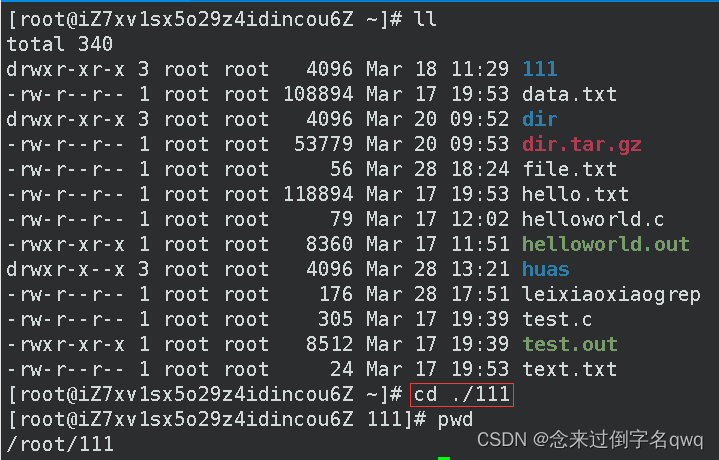
这个./其实可以省略,默认就代表当前目录下:
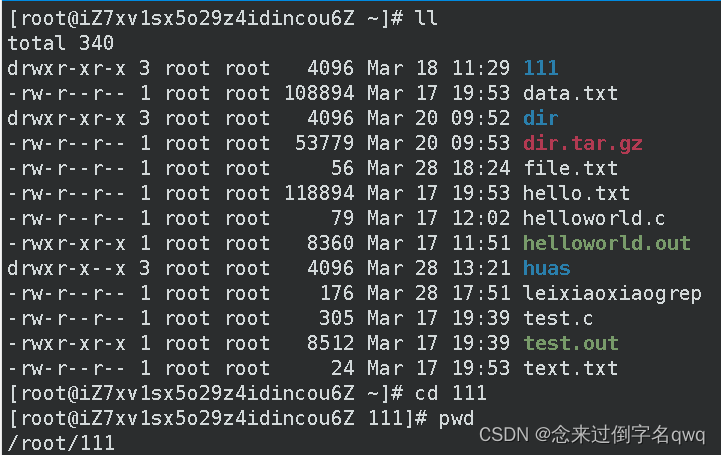
当前我在111目录,我想切换到上级目录下的dir目录:
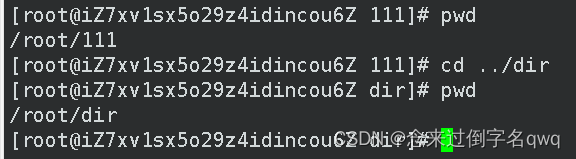
-
进入用户家目录:cd ~或cd
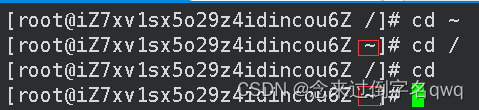
-
返回最近访问的目录:cd -(这个非常好用,比如我上次是在一个很深的目录下,然后我现在又是在别的离得较远的目录,那我想返回去就要敲很多目录名,太麻烦)。
3.5 touch 文件名(创建普通文件)
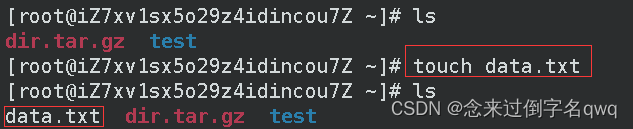
linux中不用后缀区分普通文件,都是普通文件的情况下,data.txt、data、data.a、data.abcd管什么后缀都一样。这里要说清楚的是,linux不用后缀区分文件类型,但不代表linux中安装的软件不区分,例如gcc编译器,你要是编译非.c或.cpp的文件,那肯定不行。
ls -l显示详细信息可以查看是什么文件类型,最前面的-表示是普通文件,d表示是目录,linux总共有7中文件类型,另外还有几种后续都很常用,这里先不做介绍。目前也可以通过文字颜色判断类型,白色是普通文件,蓝色是目录。

3.6 mkdir 目录名(创建目录)
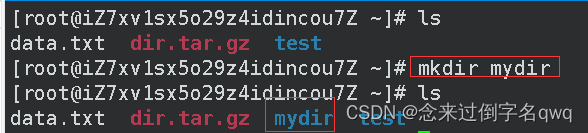
创建多级目录用-p选项:
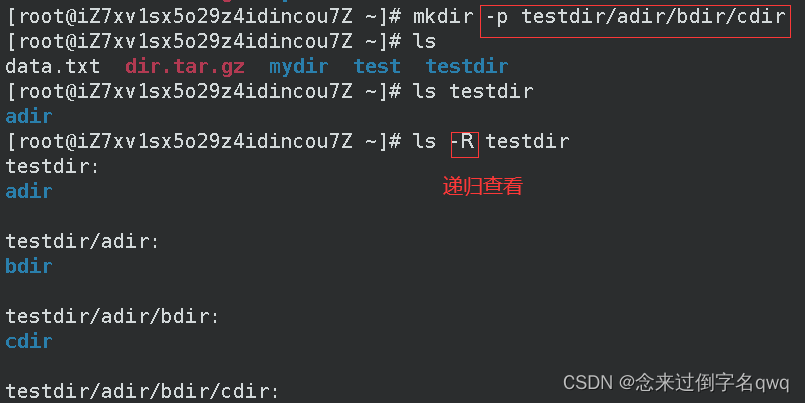
3.7 rmdir 目录名(删除空目录)
rm即remove缩写,rmdir只能删除空目录,不能删除非空目录(目录下还有其它子目录或文件)或普通文件。如果想删除非空目录,加上-p选项。
删除空目录:
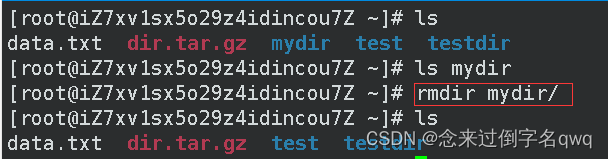
不加-p选项不能删除非空目录:
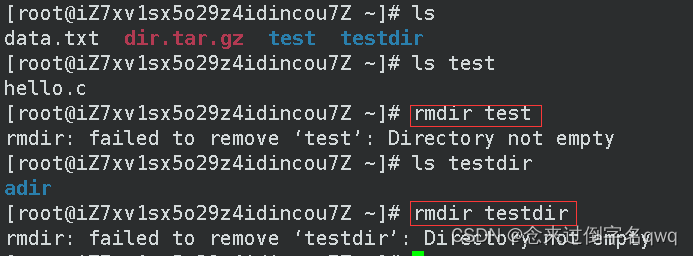
删除非空目录,要注意-p的使用方式,它代表的是当子目录为空时顺便删除父目录,所以直接删除父目录是不能全部删除的,必须删除最深的那个子目录,删除后当上级目录下为空时才删除这个上级目录:

38. rm -rf 文件或目录
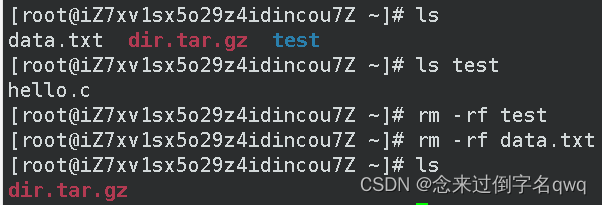
可以删除普通文件和空目录,如果想要删除非空目录,加上-r选项删除目录下与其下所有文件。一般还会加上-f,表示即便是只读文件(不能修改)也可以直接删除。
3.9 man 指令名
这个类似–help,是一个联机手册。man不仅仅是查看指令的用法,还可以查看系统调用、以及库函数等,比如man printf、man ls。

man手册分为8章,能查的东西很多,如普通命令、系统调用、库函数、文件格式等,man最经常查的是系统调用。
3.10cp [-rf] 源文件或目录 目标文件或目录(拷贝)
cp -rf src dest
-r即recurse,表示递归处理,将目录下的子文件和目录一起处理。
-f即force,强行复制文件或目录,不论这个目标文件或目录是否存在。
src(源)和dest(目标)都可以是相对路径或绝对路径,拷贝到目标文件顺便还可以顺便重命名。


3.11 mv [-f] 源文件或目录 目标文件或目录(剪切)
mv -f src dest
- 如果是剪切到同一个目录下,那功能就相当于重命名;

- 剪切到不同目录下才是剪切。

- 当然也可以同时剪切和重命名。
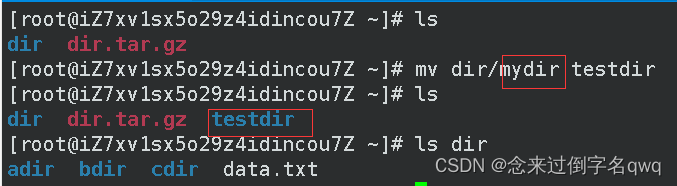
3.12 which(查看指令路径)
指令本质也是程序。
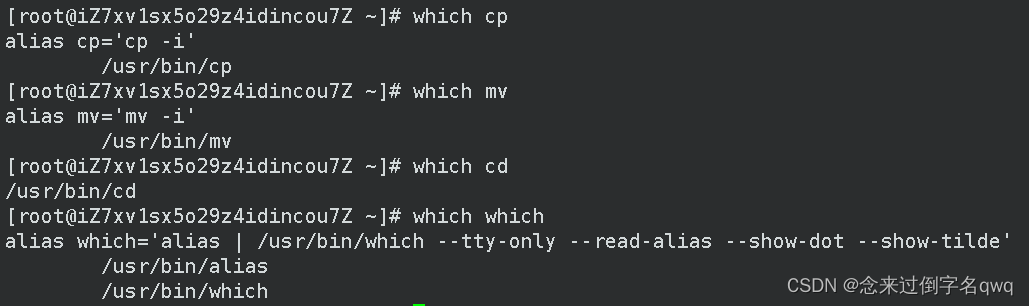
alias是对指令重命名,暂时不用管这个指令。
3.13 tree(以树状结构显示目录)
没有的话就需要安装tree指令:yum install -y tree
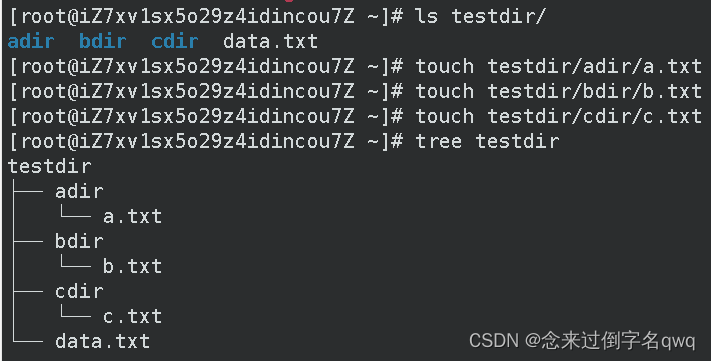 linux的文件系统是一颗多叉树,只有一个盘符。windows的文件系统也是多叉树,只不过windows可以有多个盘符,windows的文件系统也是森林结构。
linux的文件系统是一颗多叉树,只有一个盘符。windows的文件系统也是多叉树,只不过windows可以有多个盘符,windows的文件系统也是森林结构。
Ctrl + c终止任何情况
如果用tree或cat指令查看,打印内容太多停不下来,那就试试ctrl + c。
3.14 >(输出重定向)
3.1 cat [选项] 文件(查看文件内容)
常用选项:
-b:对非空行输出行号;
-n:输出所有行号;
-s:不输出多行空行。
未完待续。。。











)




)


