题目说明
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
分析
旋转图像,这个应用在图片处理的过程中,非常常见。我们知道对于计算机而言,图像,其实就是一组像素点的集合(所谓点阵),所以图像旋转的问题,本质上就是一个二维数组的旋转问题。
方法一:数学方法(转置再翻转)
我们可以利用矩阵的特性。所谓顺时针旋转,其实就是先转置矩阵,然后翻转每一行。
代码如下:
public void rotate(int[][] matrix) {int n = matrix.length;// 转置矩阵for (int i = 0; i < n; i++)for (int j = i; j < n; j++) {int tmp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = tmp;}// 翻转行for( int i = 0; i < n; i++ ){for( int j = 0; j < n/2; j++ ){int tmp = matrix[i][j];matrix[i][j] = matrix[i][n-j-1];matrix[i][n-j-1] = tmp;}}
}
复杂度分析
时间复杂度:O(N^2)
这个简单的方法已经能达到最优的时间复杂度O(N^2) ,因为既然是旋转,那么每个点都应该遍历到,N^2的复杂度不可避免。
空间复杂度:O(1)。旋转操作是原地完成的,只耗费常数空间
方法二:分治(分为四部分旋转)
方法 1 使用了两次矩阵操作,能不能只使用一次操作的方法完成旋转呢?
为了实现这一点,我们来研究每个元素在旋转的过程中如何移动。
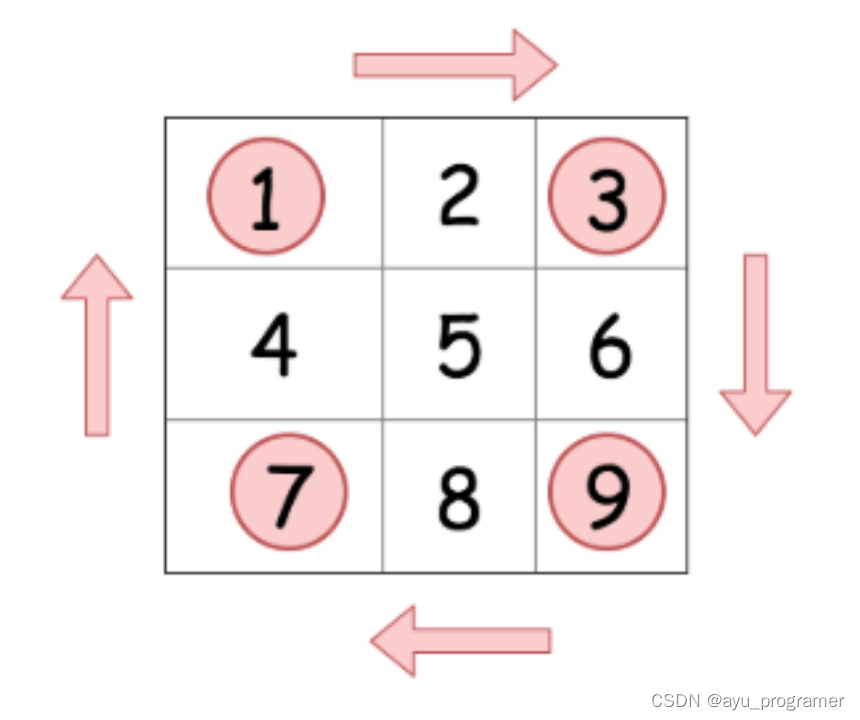
这提供给我们了一个思路,可以将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。这其实就是分治的思想。
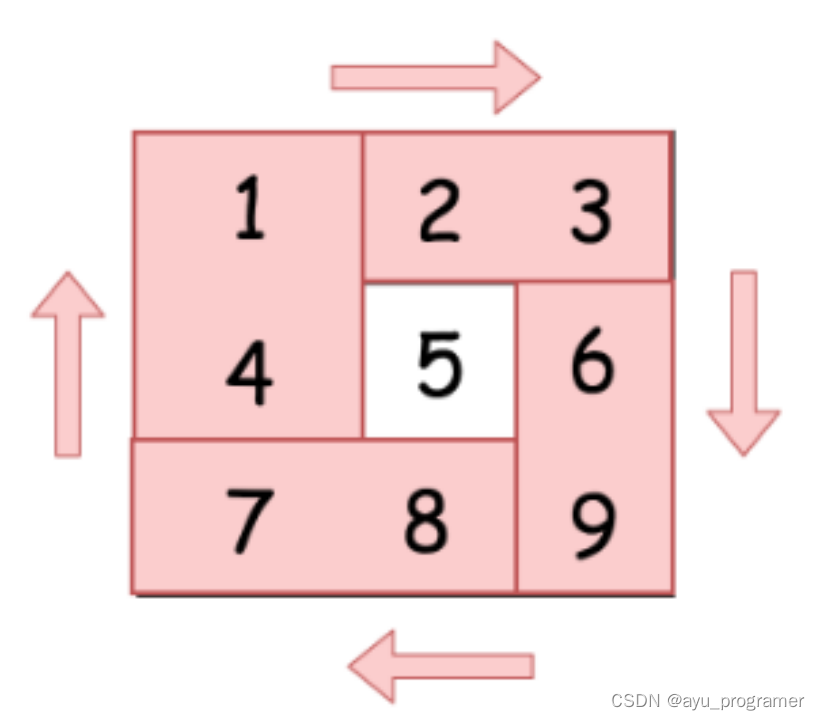
具体解法也很直接,可以在每一个矩形中遍历元素,并且在长度为 4 的临时列表中移动它们。
代码如下:
public void rotate(int[][] matrix) {int n = matrix.length;for (int i = 0; i < n / 2 + n % 2; i++) {for (int j = 0; j < n / 2; j++) {int[] tmp = new int[4];int row = i;int col = j;for (int k = 0; k < 4; k++) {tmp[k] = matrix[row][col];// 定位下一个数int x = row;row = col;col = n - 1 - x;}for (int k = 0; k < 4; k++) {matrix[row][col] = tmp[(k + 3) % 4];int x = row;row = col;col = n - 1 - x;}}}
}
复杂度分析
时间复杂度:O(N^2) 是两重循环的复杂度。
空间复杂度:O(1) 由于我们在一次循环中的操作是“就地”完成的,并且我们只用了长度为 4 的临时列表做辅助。
方法三:分治法改进(单次循环内完成旋转)
大家可能也发现了,我们其实没有必要分成4个矩阵来旋转。这四个矩阵的对应关系,其实是一目了然的,我们完全可以在一次循环内,把所有元素都旋转到位。
因为旋转的时候,是上下、左右分别对称的,所以我们遍历元素的时候,只要遍历一半行、一半列就可以了(1/4元素)。
展示代码如下
public void rotate(int[][] matrix) {int n = matrix.length;// 不区分子矩阵,直接遍历每一个元素for( int i = 0; i < (n + 1)/2; i++ ){for( int j = 0; j < n/2; j++ ){int temp = matrix[i][j]; //2,2matrix[i][j] = matrix[n-j-1][i];matrix[n-j-1][i] = matrix[n-i-1][n-j-1];matrix[n-i-1][n-j-1] = matrix[j][n-i-1];matrix[j][n-i-1] = temp;}}
}
复杂度分析
时间复杂度:O(N^2),是两重循环的复杂度。
空间复杂度:O(1)。我们在一次循环中的操作是“就地”完成的。

)
)







的计算方法和意义)

——SQL映射及缓存)






