数据结构——二叉搜索树

二叉搜索树是二叉树的一种特殊形式。二叉搜索树具有以下性质：
1.每个节点中的值必须大于（或等于）其左侧子树中的任何值
2.每个节点中的值必须小于（或等于）其右侧子树中的任何值。
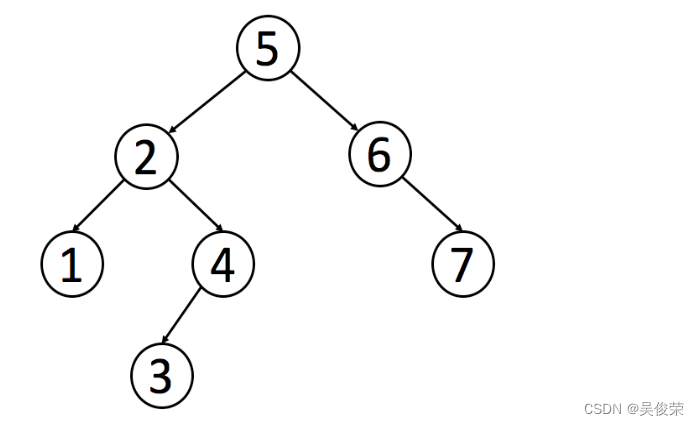
在这里插入图片描述
像普通的二叉树一样，我们可以按照前序、中序和后序来遍历一个二叉搜索树。但是值得注意的是，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。因此，中序遍历是二叉搜索树中最常用的遍历方法。

二叉树搜索：
1.如果目标值等于节点的值，则返回节点；
2.如果目标值小于节点的值，则继续在左子树中搜索；
3.如果目标值大于节点的值，则继续在右子树中搜索。

二叉树插入：
1.根据节点值与目标节点值的关系，搜索左子树或右子树；
2.重复步骤 1 直到到达外部节点；
3.根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

二叉树删除：

如果目标节点没有子节点，我们可以直接移除该目标节点。
如果目标节只有一个子节点，我们可以用其子节点作为替换。
如果目标节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该目标节点。

#include <iostream>// 定义二叉搜索树节点
struct TreeNode {int data;TreeNode* left;TreeNode* right;TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};class BinarySearchTree {
private:TreeNode* root;// 插入节点的辅助函数TreeNode* insert(TreeNode* node, int val) {if (node == nullptr) {return new TreeNode(val);}if (val < node->data) {node->left = insert(node->left, val);} else if (val > node->data) {node->right = insert(node->right, val);}return node;}// 中序遍历的辅助函数void inorderTraversal(TreeNode* node) {if (node == nullptr) {return;}inorderTraversal(node->left);std::cout << node->data << " ";inorderTraversal(node->right);}// 查找最小值的辅助函数TreeNode* findMin(TreeNode* node) {while (node->left != nullptr) {node = node->left;}return node;}// 删除节点的辅助函数TreeNode* remove(TreeNode* node, int val) {if (node == nullptr) {return node;}if (val < node->data) {node->left = remove(node->left, val);} else if (val > node->data) {node->right = remove(node->right, val);} else {if (node->left == nullptr) {TreeNode* temp = node->right;delete node;return temp;} else if (node->right == nullptr) {TreeNode* temp = node->left;delete node;return temp;}TreeNode* temp = findMin(node->right);node->data = temp->data;node->right = remove(node->right, temp->data);}return node;}public:BinarySearchTree() : root(nullptr) {}// 插入节点void insert(int val) {root = insert(root, val);}// 搜索节点bool search(int val) {TreeNode* current = root;while (current != nullptr) {if (current->data == val) {return true;} else if (val < current->data) {current = current->left;} else {current = current->right;}}return false;}// 删除节点void remove(int val) {root = remove(root, val);}// 中序遍历void inorderTraversal() {inorderTraversal(root);std::cout << std::endl;}
};int main() {BinarySearchTree bst;bst.insert(50);bst.insert(30);bst.insert(70);bst.insert(20);bst.insert(40);bst.insert(60);bst.insert(80);std::cout << "Inorder Traversal: ";bst.inorderTraversal();std::cout << "Search 60: " << (bst.search(60) ? "Found" : "Not Found") << std::endl;std::cout << "Search 90: " << (bst.search(90) ? "Found" : "Not Found") << std::endl;bst.remove(30);std::cout << "Inorder Traversal after removing 30: ";bst.inorderTraversal();return 0;
}