RetinalNet
- 概述
- 1. 引言
- 2. 相关工作
- 3. 焦点损失
- 4. RetinaNet Detector 检测器
- 5. 实验
- 6. 结论
- 3. Focal loss
- 3.1. 平衡交叉熵
- 3.2. 焦点损失定义
- 3.3. 类别不平衡和模型初始化
- 3.4. 类别不平衡和两阶段检测器
- 4. RetinaNet Detector
- 特征金字塔网络骨干(Feature Pyramid Network Backbone):
- 锚框(Anchors):
- 分类子网络(Classification Subnet):
- 边界框回归子网络(Box Regression Subnet):
- RetinaNet在推理(Inference)时的工作流程:
- 焦点损失(Focal Loss)在RetinaNet训练中的具体应用和作用
- 使用ResNet-50-FPN和ResNet-101-FPN骨干网络的初始化过程:
- RetinaNet训练过程中的优化方法和相关参数
- (a) ResNet
- (b) 特征金字塔网络(Feature Pyramid Network, FPN)
- (c) 类别子网络(Class Subnet)
- (d) 边界框子网络(Box Subnet)
概述
当然,这篇论文主要研究了一种新的损失函数——焦点损失(Focal Loss),用以改进单阶段目标检测器在处理极端类别不平衡情况时的性能。以下是论文各部分的概要总结:
1. 引言
在引言部分,论文介绍了目前目标检测的技术现状,特别是两阶段(如Faster R-CNN)和单阶段(如YOLO和SSD)检测器的性能和应用。作者指出,尽管单阶段检测器因其简洁性和速度潜力受到关注,但其准确率通常低于两阶段检测器。论文认为,这种性能差异主要是由于在单阶段检测器的训练中存在极端的前景与背景类别不平衡。为了解决这个问题,作者提出了焦点损失函数,希望通过调整损失函数来更好地关注难以分类的样本。
2. 相关工作
这部分回顾了目标检测领域的发展,包括早期的滑动窗口方法、HOG特征的引入,以及深度学习引发的变革,如R-CNN系列的进展。同时,还讨论了解决类别不平衡问题的传统方法,如难例挖掘等。
3. 焦点损失
这是论文的核心部分,详细介绍了焦点损失的概念和数学表述。焦点损失通过在交叉熵损失中引入一个调制因子(modulating factor)来减少那些易分类样本的损失贡献,使得模型更加关注那些难分类的样本。作者通过实验表明,焦点损失可以显著提高单阶段检测器在处理类别不平衡时的性能。
4. RetinaNet Detector 检测器
介绍了使用焦点损失设计的单阶段目标检测器——RetinaNet。文中详述了RetinaNet的网络架构、特征金字塔网络(FPN)的应用以及锚点框架设计。此外,还介绍了模型训练和推理的细节。
5. 实验
文中提供了一系列实验结果来证明焦点损失和RetinaNet的有效性。包括与其他现有技术的比较,不同的网络设置对结果的影响,以及焦点损失在不同参数设置下的性能测试。结果显示,RetinaNet在COCO数据集上达到了当时的最佳性能。
6. 结论
总结了焦点损失在解决单阶段目标检测中类别不平衡问题中的效果和意义,并强调了该方法的简单性和效果,为未来的研究提供了新的方向。
这篇论文通过提出一个新的损失函数,有效地解决了单阶段目标检测器面临的一个主要问题,即类别不平衡问题,并通过大量的实验验证了其有效性。
3. Focal loss
首先介绍了焦点损失(Focal Loss)的定义和动机。焦点损失是为了解决单阶段目标检测中遇到的一个极端类别不平衡问题(例如,背景和前景的比例可能达到1:1000)。
首先,文中给出了二元分类的交叉熵损失(Cross Entropy, CE)的标准形式:
- 如果真实标签 y = 1 y = 1 y=1,损失是 − log ( p ) -\log(p) −log(p);
- 如果真实标签 y = − 1 y = -1 y=−1,损失是 − log ( 1 − p ) -\log(1 - p) −log(1−p);
其中, y ∈ { + 1 , − 1 } y \in \{+1, -1\} y∈{+1,−1} 表示真实的类别标签, p ∈ [ 0 , 1 ] p \in [0, 1] p∈[0,1] 是模型预测正类标签 y = 1 y = 1 y=1 的概率。
为了表述方便,引入 p t p_t pt:
- 当 y = 1 y = 1 y=1 时, p t = p p_t = p pt=p;
- 当 y = − 1 y = -1 y=−1 时, p t = 1 − p p_t = 1 - p pt=1−p;
这样可以简化交叉熵损失的表达式为 C E ( p t ) = − log ( p t ) CE(p_t) = -\log(p_t) CE(pt)=−log(pt)。
文中指出,即使对于容易分类的样本( p t > 0.5 p_t > 0.5 pt>0.5,也就是模型对其分类相对比较自信时),交叉熵损失也会产生非平凡的大小。当许多容易分类的样本损失值累加起来时,它们的损失总和可能会淹没掉那些稀少类别的损失,导致模型训练不平衡。焦点损失的提出就是为了解决这个问题,它会通过增加一个调节因子来降低易分类样本的损失贡献,从而使模型更加专注于难分类的样本。这部分的内容是引入焦点损失背后的直观动机和数学定义的基础。
图中的内容介绍了平衡交叉熵(Balanced Cross Entropy)和焦点损失(Focal Loss)的定义以及它们是如何帮助处理类别不平衡问题的。
3.1. 平衡交叉熵
为了应对类别不平衡,一种常用的方法是引入权重因子 α α α。对于正类(foreground class)使用 α α α,对于负类(background class)使用 1 − α 1-α 1−α,其中 α α α 的值在 [ 0 , 1 ] [0, 1] [0,1] 范围内。这个权重因子可以根据类别的频率反比来设置,或者作为一个超参数通过交叉验证来确定。基于这种思想,平衡交叉熵的损失函数被定义为:
C E ( p t ) = − α t log ( p t ) CE(p_t) = -\alpha_t \log(p_t) CE(pt)=−αtlog(pt)
其中, α t \alpha_t αt 根据真实标签 y y y 的值动态调整,类似于前面定义的 p t p_t pt。
3.2. 焦点损失定义
实验表明,在训练密集检测器(dense detectors)时,由于遇到的大类别不平衡问题,易分类的负样本占据了交叉熵损失的大部分并主导了梯度。而权重因子 α α α 虽然平衡了正负样本的重要性,但它没有区分简单和困难的样本。因此,作者提出重新塑造损失函数以降低易分类样本的权重,从而更加集中于训练难分类的负样本。
焦点损失通过添加一个调节因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ 到交叉熵损失中,其中 γ γ γ 是一个可调节的焦点参数。焦点损失的数学形式如下:
F L ( p t ) = − ( 1 − p t ) γ log ( p t ) FL(p_t) = -(1 - p_t)^\gamma \log(p_t) FL(pt)=−(1−pt)γlog(pt)
焦点损失有两个主要特点:
- 当一个样本被错误分类,且 p t p_t pt 很小,调节因子接近于 1,损失几乎不受影响。而当 p t p_t pt 接近于 1 时,调节因子接近于 0,因此对于分类正确的样本,其损失将会被减少。
- γ γ γ 参数平滑地调整了易分类样本被降权的速率。当 γ = 0 时,焦点损失等同于交叉熵损失;随着 γ γ γ 的增加,调节因子的效果也会相应增强。
作者发现,在他们的实验中 γ = 2 γ = 2 γ=2 时效果最好。直观上讲,调节因子减少了易分类样本的损失贡献,扩大了样本接收低损失的范围。例如,使用 γ = 2 γ = 2 γ=2 时,一个用交叉熵损失分类准确率为 0.9 的样本,与焦点损失相比,其损失值会减少 100 倍。
最后,文章介绍了在实际中使用的 α α α 平衡的焦点损失变体,即加入了 α α α 权重的焦点损失:
F L ( p t ) = − α t ( 1 − p t ) γ log ( p t ) FL(p_t) = -\alpha_t (1 - p_t)^\gamma \log(p_t) FL(pt)=−αt(1−pt)γlog(pt)
这种形式在实验中被采用,因为它在非平衡形式上显示出了更好的准确性。最后,作者还提到,损失层的实现结合了计算 p p p 的 sigmoid 函数和损失计算,这提高了数值的稳定性。
图中的内容讨论了类别不平衡对模型初始化的影响以及在两阶段检测器中常见的处理类别不平衡的方法。
3.3. 类别不平衡和模型初始化
在二元分类模型中,默认初始化通常给予 y = − 1 y = -1 y=−1 或 y = 1 y = 1 y=1 相同的输出概率,这意味着模型最初没有偏好任何类别。但是,在类别不平衡的情况下,频繁类别造成的损失可能会在训练初期支配总损失并导致训练不稳定。为了应对这一点,作者引入了一个先验概率 ‘prior’ 用于模型对稀有类别(例如前景)的 p p p 值的初始估计,通常将这个先验值设置得很低,例如 0.01。这样的初始化改变了模型对于稀有类别的初始估计,有助于提高交叉熵和焦点损失在类别极度不平衡时的训练稳定性。
3.4. 类别不平衡和两阶段检测器
两阶段检测器通常在不使用 α \alpha α-平衡或提出的焦点损失的情况下,通过交叉熵损失进行训练。相反,它们依靠两种机制来处理类别不平衡:
- 两阶段级联:第一阶段通过目标提议机制,将几乎无限的可能对象位置减少到大约一千或两千个位置。重要的是,这些提议位置不是随机的,而是倾向于对应真实对象位置,这样可以过滤掉大部分易分类的负例。
- 偏差小批量抽样:在训练第二阶段时,通常使用偏差采样来构建包含正负样本比例为 1:3 的小批量。这个比例实际上起到了隐式的 α \alpha α-平衡作用。
作者指出,他们提出的焦点损失旨在通过损失函数直接在单阶段检测系统中解决这些问题。
总的来说,本节内容强调了在面对类别不平衡问题时,如何通过模型初始化以及损失函数的设计来改进目标检测模型的训练效果。焦点损失通过其设计直接针对这些问题提供了一个有效的解决方案。
4. RetinaNet Detector
RetinaNet是一个统一的网络,它由一个骨干网络(backbone network)和两个特定任务的子网络(subnetworks)组成:
-
骨干网络(Backbone Network):这是基础网络,负责计算输入图像的卷积特征图。这个网络是一个现成的卷积神经网络(CNN),用于提取图像的特征。
-
两个特定任务的子网络:
- 第一个子网络:负责在骨干网络输出的基础上进行卷积对象分类。
- 第二个子网络:负责进行卷积边界框回归(bounding box regression),即确定对象的位置。
这两个子网络具有简单的设计,并且是专门为单阶段、密集检测而提出的。尽管细节上有很多可能的设计选择,但大多数设计参数对具体的数值不是特别敏感,这一点在实验中有所显示。接下来的文本部分将详细描述RetinaNet的每个组件。
总体来说,这段文本强调了RetinaNet结构的简洁性和在实验中表现出的设计参数的鲁棒性,这意味着即使对于设计参数的具体值变化,模型的性能也不会有太大的影响。这样的设计使得模型在实际应用中更加灵活和稳定。
这部分内容详细介绍了RetinaNet中使用的特征金字塔网络(Feature Pyramid Network, FPN)骨干网络的结构,以及锚框(anchors)的使用方式。
特征金字塔网络骨干(Feature Pyramid Network Backbone):
- FPN概述:FPN通过在标准卷积网络顶部加上自顶向下的路径和横向连接,从单一分辨率的输入图像构建出丰富的多尺度特征金字塔。
- 多尺度特性:每一层的FPN金字塔都可以用于检测不同规模的对象。利用FPN可以改善全卷积网络(FCN)对多尺度的预测。
- 构建FPN:FPN是在ResNet架构上构建的,具体来说是从P3到P7层,每一层都有256个通道。虽然大部分设计遵循了之前的研究,但有一些小的差异。
- 重要性强调:虽然许多设计选择不是关键,但作者强调使用FPN是重要的,因为使用来自最终ResNet层的特征时,平均精度(Average Precision, AP)较低。
锚框(Anchors):
- 锚框设计:RetinaNet使用了与FPN中RPN相似的平移不变锚框。
- 锚框尺寸和比例:锚框覆盖从P3到P7层的32平方到512平方的区域,并且每个层级使用了1:2、1:1、2:1三种不同的长宽比。为了更密集的尺度覆盖,每个层级增加了子八度比例的锚框,从而改善了AP。
- 锚框总数:总共有9个锚框每个层级,并且它们覆盖了从32到813像素的尺度范围,与网络的输入图像相关。
- 锚框标签和回归目标:每个锚框被分配一个长度为K的独热编码向量来标识类别,和一个4向量用于边界框回归。
- 锚框分配规则:使用修改过的RPN规则进行多类别检测,并调整了阈值。特别是锚框分配给对象时使用了0.5的IoU阈值,并且如果锚框的IoU在[0, 0.4)之间,则分配给背景。如果一个锚框未分配(可能在[0.4, 0.5)的IoU重叠中发生),则在训练期间被忽略。
- 锚框回归:对于每个被分配的锚框,使用标准的回归目标来计算从锚框到真实对象框的偏移量。如果没有分配,则回归目标会被省略。
总的来说,这段内容强调了FPN和锚框在RetinaNet中的重要作用,并说明了它们是如何用于提高目标检测的精度和效率的。
图中内容描述了RetinaNet中的两个子网络:分类子网络(Classification Subnet)和边界框回归子网络(Box Regression Subnet)。
分类子网络(Classification Subnet):
- 这个子网络预测每个空间位置上物体存在的概率,针对A个锚点和K个对象类别。
- 它是一个小型的全卷积网络(FCN),附加在每个FPN层级上。
- 该子网络的设计很简单,使用C个通道的输入特征图,应用四个3x3卷积层,每层都有C个滤波器,并且每个卷积后都接ReLU激活函数。
- 最后,使用一个具有KA个滤波器的3x3卷积层,以sigmoid激活函数来输出KA个二进制预测,即每个空间位置上A个锚点的K个类别预测。
- 在大多数实验中,C(通道数)为256,A(每个空间位置的锚点数量)为9。
作者强调这个子网络相对于RPN是更深的,只使用3x3的卷积,并且与边界框回归子网络不共享参数。这些高层次的设计决策比具体的超参数值更重要。
边界框回归子网络(Box Regression Subnet):
- 与分类子网络并行,这个子网络负责从每个锚点到附近真实对象的偏移量回归。
- 它的设计与分类子网络相同,但终止于4A个线性输出,每个空间位置各4个输出。
- 对于每个位置的A个锚点,这四个输出预测锚点与真实对象框之间的相对偏移量。
- 使用的是R-CNN中的标准边界框参数化方式。
- 与大多数近期的工作不同,这里使用了一个与类别无关的边界框回归器,它使用的参数更少。
这两个子网络,尽管共享相似的结构,但使用不同的参数。这段内容强调了RetinaNet的两个关键组件是如何设计来专门处理目标检测中的分类和定位问题的。
RetinaNet在推理(Inference)时的工作流程:
-
RetinaNet架构: RetinaNet是一个由ResNet-FPN骨干网络、分类子网络和边界框回归子网络组成的全卷积网络(FCN)。整个网络通过这三个部分联合工作,以完成目标检测任务。
-
推理过程: 在推理阶段,输入图像简单地通过整个网络进行前向传播。这意味着图像数据会通过ResNet-FPN骨干网络来提取特征,然后这些特征会被用于分类子网络来识别物体的类别,以及边界框回归子网络来确定物体的位置。
-
提高速度的方法: 为了提高处理速度,RetinaNet在每个FPN层级只对最高分的1,000个预测进行解码,这个过程是在置信度阈值设定为0.05后进行的。也就是说,只有那些置信度高于0.05的预测才会被进一步处理。
-
最终检测结果的产生: 从所有FPN层级得到的最高分预测结果将被合并,然后应用非最大抑制(Non-Maximum Suppression, NMS)方法来去除重叠的检测框,NMS的阈值设置为0.5。通过这一步骤,可以得到最终的检测结果,即图像中物体的位置和类别。
简言之,这段内容阐明了RetinaNet如何将一个图像通过网络进行分类和位置预测,并且通过有效的筛选和NMS来产生最终的高置信度的目标检测结果。
焦点损失(Focal Loss)在RetinaNet训练中的具体应用和作用
-
焦点损失应用: 焦点损失被用作分类子网络输出的损失函数。作者发现在实践中,当焦点参数 γ = 2 \gamma = 2 γ=2 时,模型表现良好,并且RetinaNet对 γ \gamma γ 的值在 0.5 到 5 的范围内相对稳健。
-
训练中的焦点损失:在训练RetinaNet时,焦点损失应用于每张采样图像中的约100k个锚点。这与常见的做法(如使用启发式抽样的区域提案网络(RPN)或硬例挖掘(OHEM,SSD))不同,后者只在每个小批量(minibatch)中选择一小部分锚点进行计算。
-
损失计算:每张图像的总焦点损失是通过对所有约100k个锚点的焦点损失求和得出的,然后以分配给真实框(ground-truth box)的锚点数量进行归一化。这种归一化方法考虑的是分配了真实框的锚点数量,而不是总锚点数量,因为大部分锚点都是容易分类的负例,在焦点损失下会收到很小的损失值。
-
权重因子 α \alpha α:焦点损失中的 α \alpha α 用于权衡稀有类别的权重。 α \alpha α 有一个稳定的范围,但它与 γ \gamma γ 相互作用,因此选择 α \alpha α 和 γ \gamma γ 需要同步进行。一般来说,随着 γ \gamma γ 的增加, α \alpha α 应该适当减少。对于 γ = 2 \gamma = 2 γ=2,最佳的 α \alpha α 值是 0.25。
简而言之,这段文本解释了焦点损失如何集中在训练过程中的困难样本上,并如何在整个训练集上广泛应用,而不是仅仅集中在少数难分的例子上。这样做可以提高模型对罕见类别的检测能力,同时保证了模型训练的稳定性。
使用ResNet-50-FPN和ResNet-101-FPN骨干网络的初始化过程:
-
骨干网络初始化:使用在ImageNet1k数据集上预训练的基础ResNet-50和ResNet-101模型。这些模型由[16]发布,其中FPN的新层按照[20]的方法进行初始化。
-
新卷积层初始化:对于RetinaNet子网络中新增的卷积层,除了最后一层,其他都使用偏置 b = 0 b = 0 b=0 和高斯权重填充 σ = 0.01 \sigma = 0.01 σ=0.01 来初始化。
-
分类子网络的最后一层初始化:对于分类子网络的最后一层卷积层,偏置初始化设置为 b = − log ( ( 1 − π ) / π ) b = - \log((1 - \pi)/\pi) b=−log((1−π)/π)。这里 π \pi π 指定了训练开始时每个锚点被标记为前景(即有物体)的置信度。在所有实验中使用 π = 0.01 \pi = 0.01 π=0.01,尽管结果对于 π \pi π 的确切值相对稳健。
-
初始化的目的:如3.3节所解释的,这种初始化方式防止了大量背景锚点在训练的第一次迭代中产生大的、不稳定的损失值,帮助稳定了训练过程。
简言之,这段内容解释了在训练RetinaNet模型前对网络进行初始化的过程,以及如何通过特定的初始化策略来避免由于类别不平衡导致的训练不稳定。这种初始化方法特别针对大量的背景锚点,确保它们在训练开始时不会对损失函数造成巨大影响。
RetinaNet训练过程中的优化方法和相关参数
-
优化方法:RetinaNet使用随机梯度下降(Stochastic Gradient Descent, SGD)进行训练。
-
SGD同步:在8个GPU上使用同步SGD,每个GPU处理2张图像,因此每个小批量(minibatch)包含16张图像。
-
迭代次数和学习率:模型默认训练90k迭代次数,初始学习率设为0.01。在60k和80k迭代时,学习率分别除以10。
-
数据增强:除非另有说明,否则只使用水平翻转作为数据增强方法。
-
权重衰减和动量:权重衰减设置为0.0001,动量设置为0.9。
-
损失函数:训练损失是焦点损失和用于边界框回归的标准平滑L1损失的和。
-
训练时间:训练时间在10到35小时之间,具体取决于Table 1e中的模型。
这段内容为希望重现RetinaNet模型或理解其训练过程的研究者提供了重要的技术细节。
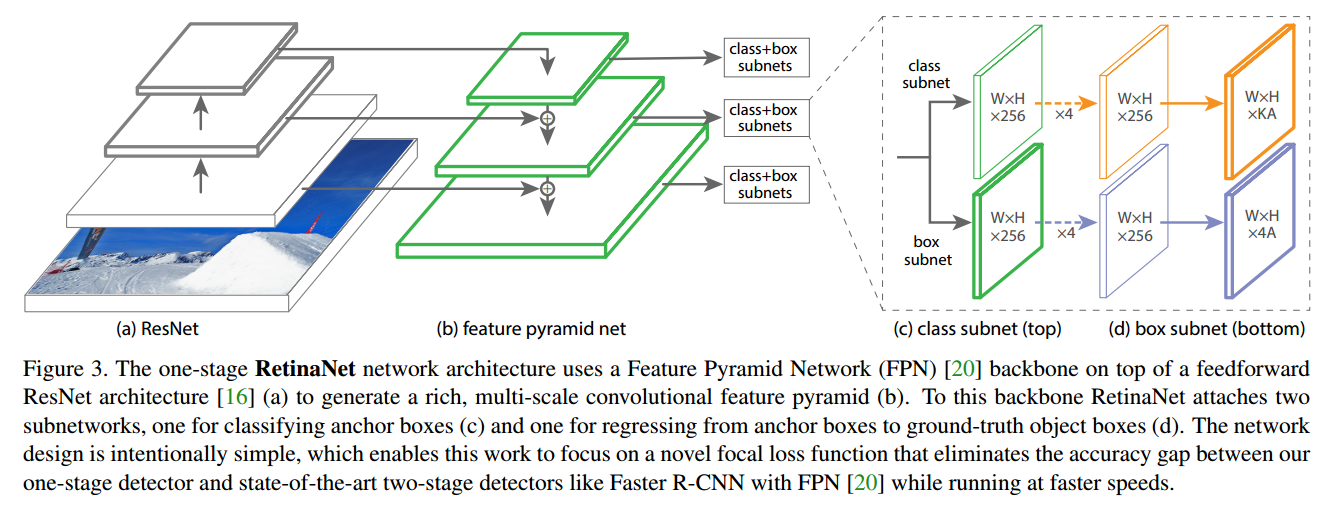
这张图是论文中关于RetinaNet架构的详细说明,它展示了RetinaNet的主要组件及其工作方式。图由四个部分组成:
(a) ResNet
这部分展示了ResNet架构,它是RetinaNet的 backbone 网络。ResNet 利用残差连接来构建深度神经网络,以便在不丧失训练效率的前提下捕捉丰富的特征。这里的图像表明,输入图像通过不同层的处理,生成了不同分辨率的特征图。
(b) 特征金字塔网络(Feature Pyramid Network, FPN)
特征图经过FPN进行多尺度处理。FPN结构通过顶层到底层的路径和横向连接增强了特征层之间的信息流,它能够生成一系列尺度不同的特征图,每个特征图都包含了原始图像的丰富语义信息和空间信息。这些特征图被用于检测不同大小的对象。
© 类别子网络(Class Subnet)
类别子网络用于对锚框(anchor boxes)进行分类。它由多个卷积层和ReLU激活函数构成,并且输出每个空间位置上的锚框的类别分数。每个卷积层的尺寸都是WxH,并且有256个通道。最后一层卷积输出的尺寸是WxH,有KA个通道,其中K是类别的数量,A是每个位置锚框的数量。
(d) 边界框子网络(Box Subnet)
边界框子网络负责根据锚框回归到真实对象框(ground-truth object boxes)。这个子网络的结构与类别子网络类似,包含多个卷积层和ReLU激活函数,但它输出的是每个锚框的四个坐标偏移量,用于从锚框精确预测对象的位置。输出尺寸同样是WxH,但通道数是4A,代表每个锚框的4个坐标。
整个RetinaNet架构的设计意在简洁高效,目的是在保持或提升两阶段检测器(如带有FPN的Faster R-CNN)的准确性的同时,实现更快的检测速度。通过结合FPN和ResNet的深度学习模型,并引入焦点损失,RetinaNet在单阶段检测器中取得了优异的性能。
Initialization: We experiment with ResNet-50-FPN and ResNet-101-FPN backbones [20]. The base ResNet-50 and ResNet-101 models are pre-trained on ImageNet1k; we use the models released by [16]. New layers added for FPN are initialized as in [20]. All new conv layers except the final one in the RetinaNet subnets are initialized with bias b = 0 b = 0 b=0 and a Gaussian weight fill with σ = 0.01 σ = 0.01 σ=0.01. For the final conv layer of the classification subnet, we set the bias initialization to b = − log ( ( 1 − π ) / π ) b = − \log((1 − π)/π) b=−log((1−π)/π), where π π π specifies that at the start of training every anchor should be labeled as foreground with confidence of ∼ π ∼π ∼π. We use π = . 01 π = .01 π=.01 in all experiments, although results are robust to the exact value. As explained in 3.3, this initialization prevents the large number of background anchors from generating a large, destabilizing loss value in the first iteration of training.


![Failed to resolve ‘bss.myhuaweicloud.com‘ ([Errno -2] Name or service not know](http://pic.xiahunao.cn/Failed to resolve ‘bss.myhuaweicloud.com‘ ([Errno -2] Name or service not know)




)


)
)
)





在科学文献摘要领域的应用)
