回溯算法初识

什么是回溯算法

​ 回溯算法是一种通过不断尝试可能的解决方案来解决问题的算法。它通常用于解决组合优化问题，如排列组合问题、子集和问题等。该算法通过尝试所有可能的候选解，并逐步构建解决方案。在构建过程中，如果发现当前的解决方案不满足问题的条件，则回溯到上一步，尝试其他的选择。

回溯算法的步骤

回溯算法的一般步骤如下：

• 定义问题的解空间：将问题转化为在解空间中搜索问题解的问题。解空间树是问题的解空间的一种形象化表示，树的每个节点对应一个问题的状态或者可能的解。

• 确定候选解：在每一步尝试中，确定当前可选的候选解。这通常涉及到从问题状态的某些方面生成新的状态。

• 检查约束条件：对于生成的候选解，检查是否满足问题的约束条件。如果候选解不满足约束条件，则丢弃该解，否则继续下一步。

• 递归尝试：对满足约束条件的候选解，进行递归尝试。在下一层递归中，继续重复步骤 2 到步骤 4，直到找到问题的解或者确定问题无解。

• 回溯：如果当前候选解无法满足问题的要求，或者在递归尝试过程中发现无解，则需要进行回溯。回溯是指退回到前一步的状态，尝试其他的候选解。在回溯的过程中，通常需要撤销之前的选择，恢复到上一步的状态。

• 重复搜索：重复步骤 2 到步骤 5，直到找到问题的解或者确定问题无解。

这些步骤描述了一般的回溯算法的流程，具体问题的实现可能会有所不同，但通常都是在这个框架下进行的。

回溯算模版

回溯算法代码框架如下：

void backtrack(/* 参数列表 */) {if (/* 终止条件满足 */) {/* 处理结果，如将解加入结果集合 */return;}for (/* 遍历所有可行的选择 */) {if (/* 不满足选择的条件 */) {continue;}/* 做出选择 *//* 更新状态 */backtrack(/* 参数列表 */); // 递归调用backtrack函数/* 恢复状态，撤销上一步的选择 */}
}

遍历过程如图：

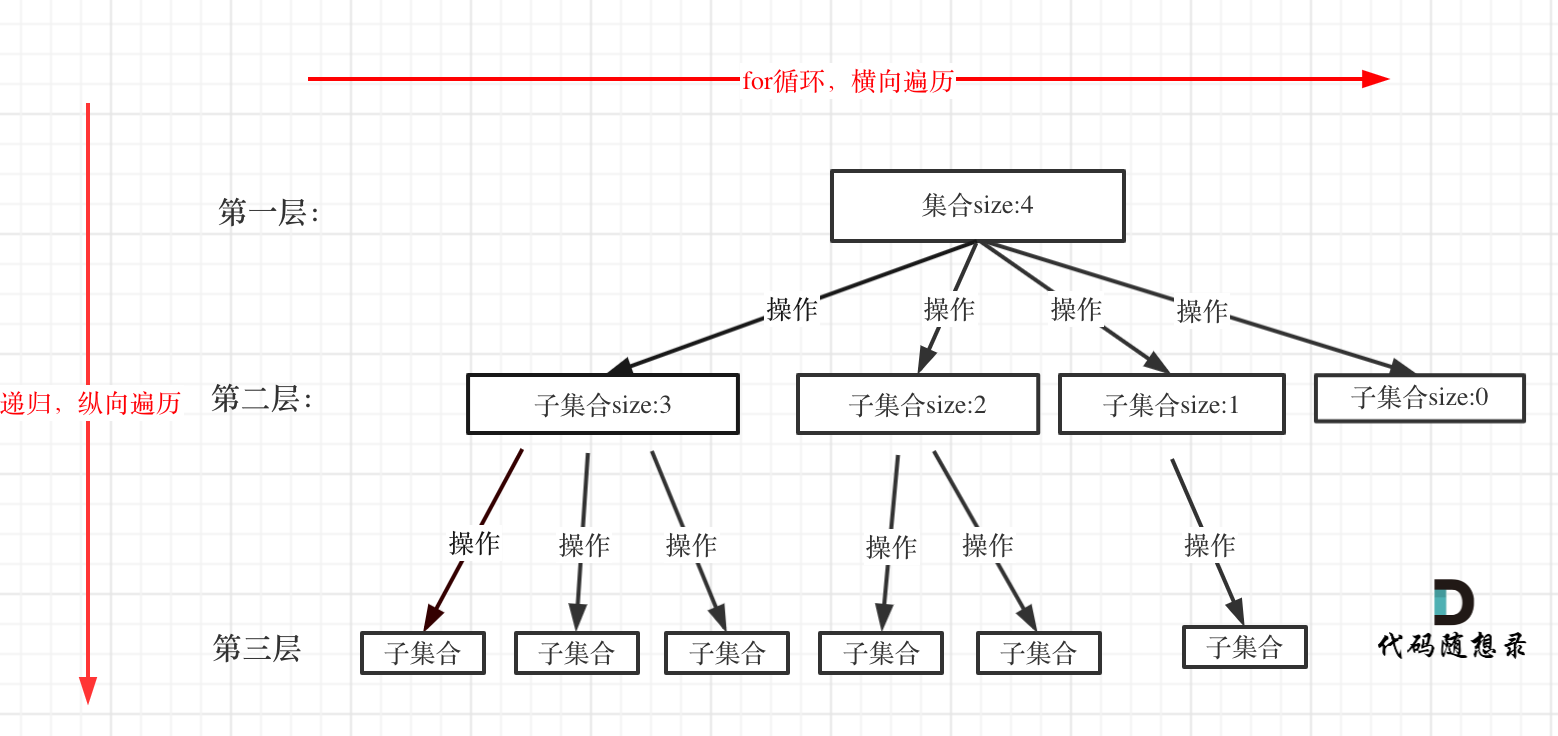
例题

77. 组合

本题就需要我们运用回溯算法去实现。

int* path;              // 存储当前路径的数组
int pathTop;            // 当前路径的栈顶指针
int** ans;              // 存储最终结果的二维数组
int ansTop;             // 最终结果数组的栈顶指针// 回溯函数，寻找组合
void backtracking(int n, int k, int startIndex) {if (pathTop == k) { // 如果当前路径长度等于所需长度int* temp = (int*)malloc(sizeof(int) * k); // 分配临时数组int i;for (i = 0; i < k; i++) {temp[i] = path[i]; // 将当前路径复制到临时数组}ans[ansTop++] = temp; // 将临时数组添加到最终结果数组中return;}int j;for (j = startIndex; j <= n; j++) { // 从起始位置到 n 循环path[pathTop++] = j; // 将当前元素添加到路径中backtracking(n, k, j + 1); // 递归调用，寻找下一个元素pathTop--; // 回溯，撤销选择}
}// 组合函数，返回所有长度为 k 的组合
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {path = (int*)malloc(sizeof(int) * k); // 分配路径数组ans = (int**)malloc(sizeof(int*) * 1000000); // 分配最终结果数组的空间pathTop = ansTop = 0; // 初始化栈顶指针backtracking(n, k, 1); // 调用回溯函数开始寻找组合*returnSize = ansTop; // 设置返回结果的大小*returnColumnSizes = (int*)malloc(sizeof(int) * (*returnSize)); // 分配返回结果每行的列数数组的空间int i;for (i = 0; i < *returnSize; i++) {(*returnColumnSizes)[i] = k; // 设置每行的列数为 k}return ans; // 返回最终结果数组
}

已经到底啦！！