概述
为了实现哈希集合这一数据结构，有以下几个关键问题需要解决：
- 哈希函数：能够将集合中任意可能的元素映射到一个固定范围的整数值，并将该元素存储到整数值对应的地址上。
- 冲突处理：由于不同元素可能映射到相同的整数值，因此需要在整数值出现「冲突」时，需要进行冲突处理。总的来说，有以下几种策略解决冲突：
-
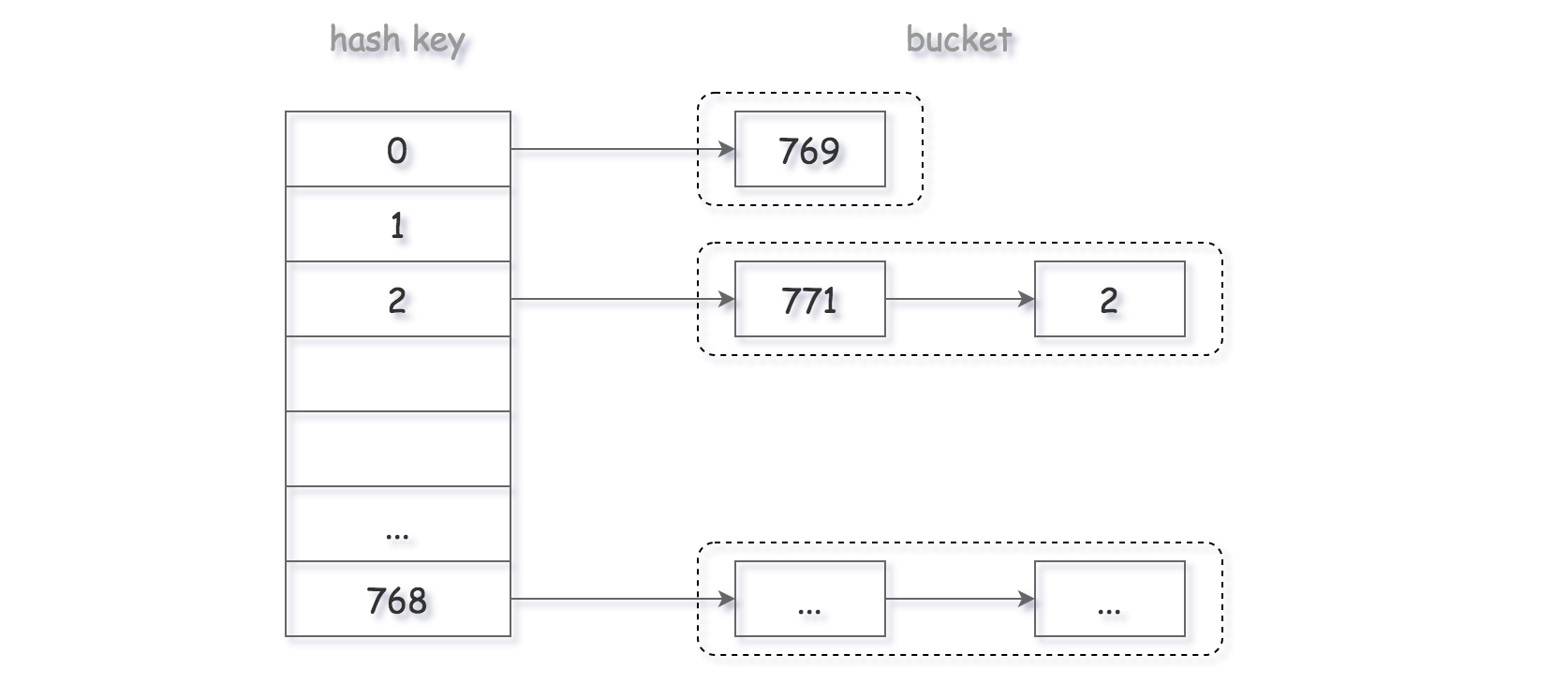
链地址法：为每个哈希值维护一个链表，并将具有相同哈希值的元素都放入这一链表当中。
-
开放地址法：当发现哈希值 hhh 处产生冲突时，根据某种策略，从 h h h出发找到下一个不冲突的位置。例如，一种最简单的策略是，不断地检查 h + 1 , h + 2 , h + 3 , … h + 1 , h + 2 , h + 3 , … h + 1 , h + 2 , h + 3 , … h+1,h+2,h+3,…h+1,h+2,h+3,\ldots h+1,h+2,h+3,… h+1,h+2,h+3,…h+1,h+2,h+3,…h+1,h+2,h+3,… 这些整数对应的位置。
-
再哈希法：当发现哈希冲突后，使用另一个哈希函数产生一个新的地址。
-
- 扩容：当哈希表元素过多时，冲突的概率将越来越大，而在哈希表中查询一个元素的效率也会越来越低。因此，需要开辟一块更大的空间，来缓解哈希表中发生的冲突。
以上内容读者可以自行翻阅数据结构的教材，本题解不再阐述，而是直接给出一个最简单的哈希表实现。
方法一：链地址法
设哈希表的大小为 base \textit{base} base，则可以设计一个简单的哈希函数： h a s h ( x ) = x mod b a s e hash(x) =x \, \text{mod}\, base hash(x)=x mod base。
我们开辟一个大小为 b a s e base base 的数组，数组的每个位置是一个链表。当计算出哈希值之后，就插入到对应位置的链表当中。
由于我们使用整数除法作为哈希函数，为了尽可能避免冲突，应当将 b a s e base base 取为一个质数。在这里，我们取 b a s e = 769 base=769 base=769。
相关题目
705. 设计哈希集合
