算法100道经典例子,按算法与数据结构分类
- 1、祖玛游戏
- 2、找下一个更大的值
- 3、换根树状dp
- 4、一笔画完所有边
- 5、树状数组,数字1e9映射到下标1e5
- 6、最长回文子序列
- 7、超级洗衣机,正负值传递次数
- 8、Dijkstra
- 9、背包问题,01背包和完全背包
- 10、矩阵生成未被选过的随机点
- 11、寻找符合要求的矩形区域
- 12、找出第k大的子序列和
- 13、从nums中选k个不相交子数组,使得总能量最大
- 14、加密解密,全局ID生成器
- 15、多种情况的动态规化如何做
- 16、多种情况的动态规化如何做2
- 17、查找n最近的回文数
- 18、分数最少,且字典序最小
- 19、删除元素,使其出现频率满足要求
- 20、max(区间最小值*区间长度)
- 21、从示例中找规律
- 22、凸包问题——Andrew算法
- 23、从左上角到右下角的最小步数
- 24、判断四个点是否是正方形
- 25、最大的频率
- 26、最长公共后缀,字典树
- 27、二维接雨水
- 28、三指针,固定其一,相向移动其二
- 29、相同任务之间须有间隔,求最短完成时间
- 30、循环队列如何判断null和full
- 31、Dijkstra设计题
- 32、从俩数组挑选n种元素
- 33、一次跳跃的线性遍历,dp+前缀和
- 34、从每个数组中选一个数组成最小区间
- 35、最大或值,最短长度的子数组
- 36、删除一个点后最小的最大曼哈顿距离
- 37、双指针找链表环形,以及环形的首
- 38、可以组成排序二叉树的数组
- 39、第k个祖先
- 40、位运算求相同数目1的略大和略小的数
- 41、位运算计算乘法
- 42、有重复元素的全排列怎么写?
1、祖玛游戏

- 这道题要思考的问题比较多,首先求最少球数,想到用二分来做,但是每次二分,看用m个球是否能消除board是绕远路了,直接广度或者深度+记忆化搜索更直接
- 广度每次保存状态,用vis=100101不如直接把字符串当状态要方便,每次放球和消除相当于重新构建一个字符串,状态由board、hand、已用球数这三个变量构建
- 每次放球放在哪里?直接说结果,放在可消除连续球的一边,或者两个相同球的中间,详见代码
- 每次放完球如何重复消除?用栈维护遍历的连续球,遍历时维护球的种类和个数,如果在一段相同球遍历结束后,前一段个数大于3,就消除,例如1122211,中间的222在第3个1时消除,第3个1遍历时还能把个数加到前面的连续段中,从而实现连续消除
func findMinStep(board string, hand string) int {// 每轮,用哪个球?放在哪个位置最优?// 红+红红、红红+红、红+红+红,这三种情况没有区别,那设定统一放左边// 每轮放球只有三种可能,与右球颜色相同,与两侧球颜色不同、且两侧球颜色相同,与两侧球颜色不同、且两侧球颜色不同// 前两种情况都有可能达成最优解,第三种情况并不比前两种更优,下面分别给出两个示例// 11223311 - 1123,插2插3,只需两个即可消除// 1122113311 - 23,插2插3,112211(3)331(2)1,直接全消除,所需两个// 如何实现连续消除?// 遍历桌上球cur,用一个栈维护遍历球的种类和数量,栈中最后一种球last// 每次遍历到cur回头检查last是否颜色不同且超过3个,true则出栈,如果栈空或者cur与last不同,cur入栈且cur++,否则last++clean := func(s string)string{n := len(s)// 分别记录种类和数量stack1 := make([]byte, n)stack2 := make([]int, n)idx := 0for i := range s{cur := s[i]for idx>0 && cur!=stack1[idx-1] && stack2[idx-1]>=3{idx--}if idx==0 || cur!=stack1[idx-1]{stack1[idx] = curstack2[idx] = 1idx++}else if cur==stack1[idx-1]{stack2[idx-1]++}}for idx>0 && stack2[idx-1]>=3{idx--}res := ""for i:=0;i<idx;i++{res += strings.Repeat(string(stack1[i]), stack2[i])}return res}// 假设board+hand组成一种状态,不同顺序放球所达到的状态有可能是相同的// 穷尽所有情况求最少放球数,用广度优先遍历,或者深度+记忆化搜索,我们用广度// 状态用字符串表示,方便插入消除字符type states struct{board stringhand stringstep int}q := []states{states{board,hand,1}}// 已访问过的状态cnt := map[string]bool{(board+"-"+hand): true}for len(q)>0{curBoard,curHand,step := q[0].board,q[0].hand,q[0].stepfor i,c1 := range curBoard{isUsed := map[byte]bool{}for j,c2 := range curHand{// 剪枝,对于同一个位置,每种球用几次都是一样的if isUsed[byte(c2)]{continue}isUsed[byte(c2)] = true// 两种情况才放球:与右球颜色相同,与两侧球颜色不同、且两侧球颜色相同if c1==c2 || (c1!=c2 && i>0 && byte(c1)==curBoard[i-1]){// 将c2插入c1前面newBoard := curBoard[:i]+string(c2)+curBoard[i:]// 重复消除newBoard = clean(newBoard)newHand := curHand[:j]+curHand[j+1:]if len(newBoard)==0{// 全部消除,广度的第一个结果就是最短的return step}if !cnt[newBoard+"-"+newHand]{cnt[newBoard+"-"+newHand] = trueq = append(q, states{newBoard,newHand,step+1})}}}}fmt.Println(step)q = q[1:]}return -1
}
2、找下一个更大的值

- 正向思考,遍历i找j,反向思考,遍历j找i
- 在遍历j时记录在一个队列中,每次从队列尾开始和j比较,如果小于j,就找到了一组i和j,然后抛出i,最后加入j,这样每次从队尾抛出更小的,使得队列呈现一种单调递减的趋势,类似单调栈,但是由于要找下一个元素,限制了相对位置,所以不能用单调栈,而是用队列
func nextGreaterElements(nums []int) []int {// 正向思路,遍历i找j,反向思路,遍历j找i// 维护一个队列,遍历j,和最后加入的下标比较,如果更小,就确定了i,更新结果// 由于每次从队尾抛出更小的元素,所以最后队列呈现单调不增的趋势,就像是单调递增栈n := len(nums)res := make([]int,n)// 对于nums[n-1],他的j可能是n-2,所以需要遍历到n+n-2,即2*n-1次q := make([]int,0,2*n-1)for i:=0;i<2*n-1;i++{if i<n{// 顺便初始化res[i] = -1}for len(q)>0 && nums[q[len(q)-1]]<nums[i%n]{res[q[len(q)-1]] = nums[i%n]q = q[:len(q)-1]}q = append(q,i%n)}return res
}
3、换根树状dp

-
最开始思路是暴力模拟,假设0~n为根,统计假设中在猜测里的个数,如果大于k就加到res中,但是这样做复杂度很高
-
实际上假设x为根和假设y为根只有x和y的相对关系是不同的,其他节点和xy的相对关系不变
-
-
我们完全可以只dfs以0为根的情况,然后通过换根,如果(x,y)在猜测中就减一,如果(y,x)在猜测中就加一,来计算其他所有节点为根的情况,最后得到总和
func rootCount(edges [][]int, guesses [][]int, k int) int {// 模拟,以x为根统计正确的个数,接着以y为根// 存在猜想(x,y)时正确数减一,存在猜想(y,x)时正确数加一// 建表n := len(edges)+1table := make([][]int,n)for _,arr := range edges{table[arr[0]] = append(table[arr[0]],arr[1])table[arr[1]] = append(table[arr[1]],arr[0])}// n<1e5,key可以用x*1e6+y来代替offset := 1000000cnt := map[int]int{}for _,arr := range guesses{cnt[arr[0]*offset+arr[1]] = 1}// 先假设以0为根节点var dfs func(int,int)intdfs = func(x,fa int)int{res := 0for _,y := range table[x]{if y!=fa{if cnt[x*offset+y]==1{res++}res += dfs(y,x)}}return res}num0 := dfs(0,-1)// 从x换根到y,加上(y,x),减去(x,y),其他节点相对x,y的位置不变,猜对个数也不变// 示意图:其他<-x->y->其他,其他<-x<-y->其他res := 0// 从fa到x,再从x到y,计算统计正确个数,若大于k,就加到res中var redfs func(int,int,int)redfs = func(x,fa,numx int){if numx>=k{res++}for _,y := range table[x]{if y!=fa{redfs(y,x,numx-cnt[x*offset+y]+cnt[y*offset+x])}}}redfs(0,-1,num0)return res
}
其中,redfs也可以用dp来写,也就是换根dp
dp := make([]int,n)dp[0] = num0if dp[0]>=k{res++}for i:=1;i<n;i++{// 从i到某个jfor _,j := range table[i]{if j<i{dp[i] = dp[j]-cnt[j*offset+i]+cnt[i*offset+j]if dp[i]>=k{res++}break}}}
4、一笔画完所有边
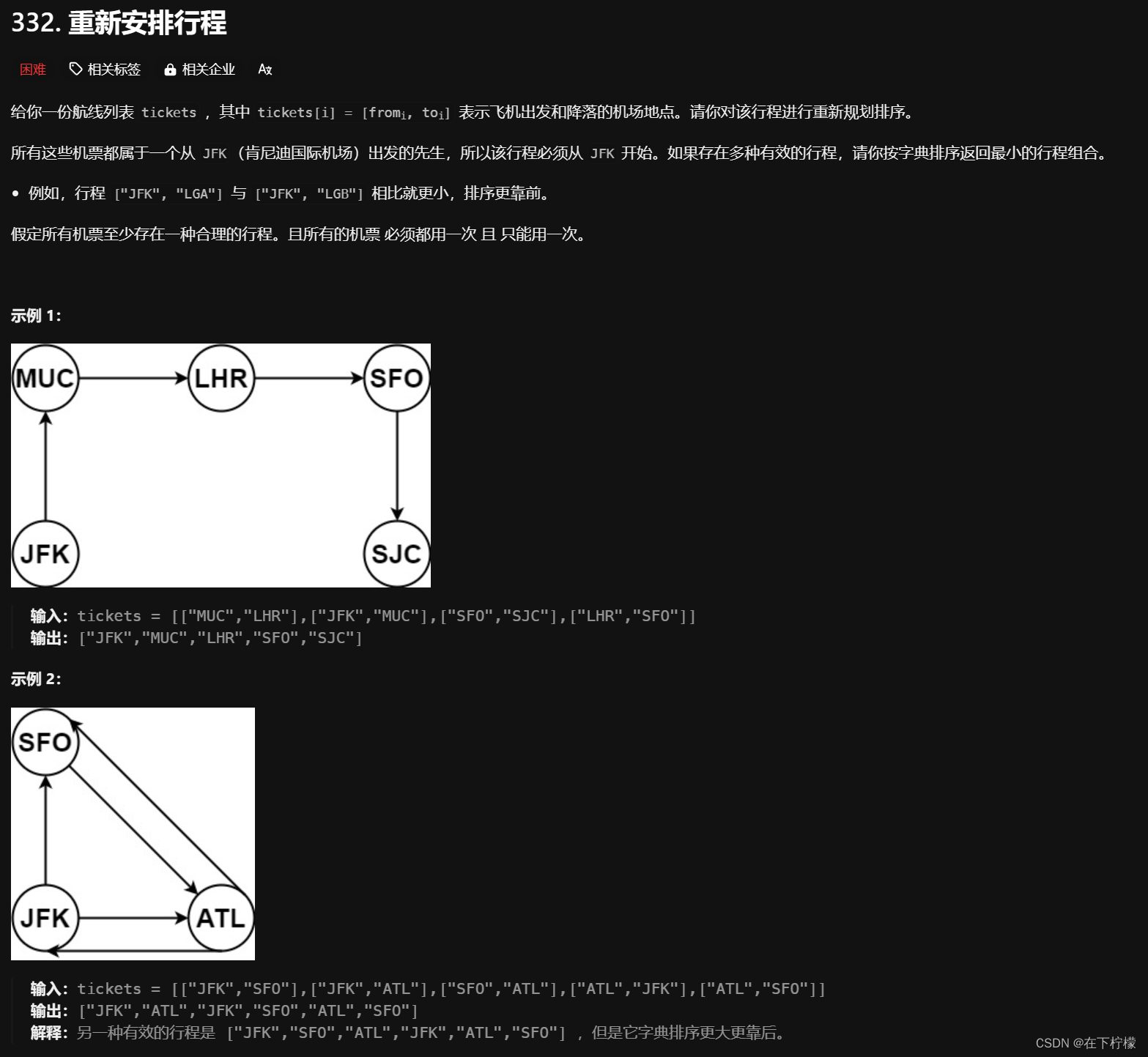
- 本题直接深度优先遍历,对每个节点出发的边排序,记录使用情况只能通过部分测试用例,最后一个用例比较特殊,需要我们逆向思考问题
- 题目说必定有一种行程安排,那存在两种情况,没有死胡同和有死胡同,没有死胡同就是这个图从哪个节点出发都可以走一遍,有死胡同就是这个图存在一个节点直接能进或者只能出,由于固定出发节点SFK,所以死胡同是入度比出度大1,我们通过dfs(SFK)控制出发的起点,在遍历table[x]时,只有把x的出度都遍历一遍才把x加入res,通过控制出度来控制出发的终点,这样就能降低复杂度,通过最后一个特殊用例
- 如果出度为0才能加入res,那res是逆序的,最后还要翻转一下
// 这个问题类似于一笔画完所有边
// 题目保证了必有一个答案,即要么没有死胡同,要么存在一个死胡同,只能出或进一次
// 死胡同的情况是有一个节点入度和出度差1,由于固定JFK为出发点,那这个死胡同的节点必定是终点,入度比出度大1
// 那我们逆向思考,如果一个节点的出度都遍历完了,才加入res中,最后将res翻转即可
// 这样起点由第一个dfs传参控制,终点由上述规则控制,第一个得到的结果就是答案
func findItinerary(tickets [][]string) []string {// 建表g := map[string][]string{}// 排序后每次贪心遍历字典序最小的机票,所以无需记录机票是否用过for _,arr := range tickets{x,y := arr[0],arr[1]g[x] = append(g[x],y)}// 排序for k := range g{sort.Strings(g[k])}res := make([]string,0,len(tickets)+1)var dfs func(string)dfs = func(x string){// 遍历从x出发的机票,只有x的出度为0时才加入到res中for {if v,ok:=g[x];!ok || len(v)==0{res = append(res,x)break}y := g[x][0]// 这里直接删除遍历过的节点,在每个节点的遍历中,由出度的数量控制加入res的时间// 例如当前y可以完成出度遍历,加入res,但是x还有除了y以外的节点未遍历,所以还要接着遍历,直到出度为0// 上述情况由于题目声明一定有一个路径,所以x出发之后可以回到x,那时再到yg[x] = g[x][1:]dfs(y)}return}dfs("JFK")for i:=0;i<len(res)/2;i++{res[i],res[len(res)-1-i] = res[len(res)-1-i],res[i]}return res
}
5、树状数组,数字1e9映射到下标1e5
func resultArray(nums []int) []int {// 树状数组// 线段树是将0-n拆成0-n/2,n/2+1-n,装入一个一维数组中,递归次数为下标,2i,2i+1// 树状数组是将0-n拆分成2的幂,例如i=15=8+4+2+1// 离i越近越细分,所以拆分成15-15,14-13,12-9,8-1这四个数组,左闭右闭// 由于拆成2的幂,所以下标i中有几个二进制1就拆分成几个数组,修改复杂度是O(logn)// 递归的拆分,i->i-lowbit(i)->...->1,15->14->12->8// 如何查找?递归查找i-lowbit(i),例如查找[1,x]递归累加dfs(x),查找[l,r]=dfs(r)-dfs(l-1)// 如何更新?如果i发生改变,那依次改变i+lowbit(i)直到n// 例如i=5=ob0101,n=10,更新5,6,8,区间表示是[5,5],[5,6],[1,8],数组表示是g[5],g[6],g[8]// 如何维护?记录在一维数组tree中,tree[i]中记录[i-lowbit(i)+1,i]这个区间的一些属性值,可以是一个数组,可以是一个结构体// 由此树状数组基本成型,查找和更新的复杂度都是O(nlogn)// 树状数组// 维护一个长为1e9的数组,每加入一个数在对应位置、以及所属的后续位置+1,查询时累加小于v,即[1,v]的个数,然后1e9-[1,v]即可// 注意到1e9太大,而n=1e5长度适中,不保存数字v,而是v的下标i,对nums排序sorted := slices.Clone(nums)slices.Sort(sorted)// 如果有重复元素,那他们的下标会不同,即相同v对应不同i,所以要去重sorted = slices.Compact(sorted)m := len(sorted)arr1,arr2 := nums[:1],[]int{nums[1]}t1,t2 := make([]int, m+1),make([]int, m+1)// 向arr加入v,向tree[i]累加1add := func(tree []int, i int){for i<m+1{tree[i]++// i+lowbit(i)i += i & -i}}// 查询小于v,即小于i的元素和pre := func(tree []int, i int)int{res := 0for i>0{res += tree[i]// i-lowbit(i)i -= i & -i}return res}// 下标+1,目的是让0空出来,树状数组是对二进制1的个数计算的,所以避开0add(t1, sort.SearchInts(sorted, arr1[0]) + 1)add(t2, sort.SearchInts(sorted, arr2[0]) + 1)for _,x := range nums[2:]{i := sort.SearchInts(sorted, x)+1// 大于i的个数=总数-小于i的个数=greaterCountnum1 := len(arr1) - pre(t1, i)num2 := len(arr2) - pre(t2, i)if num1>num2 || num1==num2 && len(arr1)<=len(arr2){arr1 = append(arr1, x)add(t1, i)}else{arr2 = append(arr2, x)add(t2, i)}}return append(arr1, arr2...)
}
6、最长回文子序列

- 动态规划,如果是二维数组
dp[i][j],那比较简单,但是如果要求O(n)空间复杂度呢? - 注意到二维数组的更新顺序是i=n-10,j=i+1n-1,随着i的递减,每轮更新的j的数量递增,最大为n,那可以只在一个一维数组中进行维护
- 对于每个i,j,只会有三种情况,一种是上一轮i+1计算的j,由于数组没有刷新,所以残留在dp[j]中,一种是两端字符匹配,那i+1的情况下dp[j-1]+2,所以本轮在遍历j时需要在赋值前记录dp[j]以供后续使用,一种是本轮i的j-1,直接取值即可
- 从O(n2)空间复杂度压缩到O(n),真是妙不可言
func longestPalindromeSubseq(s string) int {n := len(s)// dp[j]表示在i的情况下,[i:j]中最长回文子序列的长度// 随着i的变化,dp[j]的意义发生改变,最后i=0,返回dp[n-1]即可// dp[i:j]只有三种可能,dp[i+1:j],dp[i+1:j-1]+2和dp[i:j-1]// 而一维数组dp[j]的值本来就是上一轮i+1计算的值,即dp[i+1:j]// 而dp[i+1:j-1]正是上一轮遍历的i的情况下的dp[j-1],实在是妙不可言dp := make([]int,n)dp[n-1] = 1for i:=n-1;i>=0;i--{// 初始化dp[i] = 1temp := 0for j:=i+1;j<n;j++{// 如果两端字符匹配那直接dp[i+1:j-1]+2,其余两种情况不会比它更大// 如果没匹配上直接比较其余两种情况if s[i]==s[j]{// dp[i+1:j-1]+2的情况,并更新temp为dp[i+1:j]以供dp[i,j+1]使用temp,dp[j] = dp[j],temp+2}else{// 在赋值前更新temp,此时的dp[j]中残留i+1的情况// 对于后面i-1和j+1来说,temp就是dp[i+1:j-1]temp = dp[j]// dp[i:j-1]的情况,注意此时的dp[j]中是dp[i+1:j]dp[j] = max(dp[j], dp[j-1])}}}return dp[n-1]
}
7、超级洗衣机,正负值传递次数
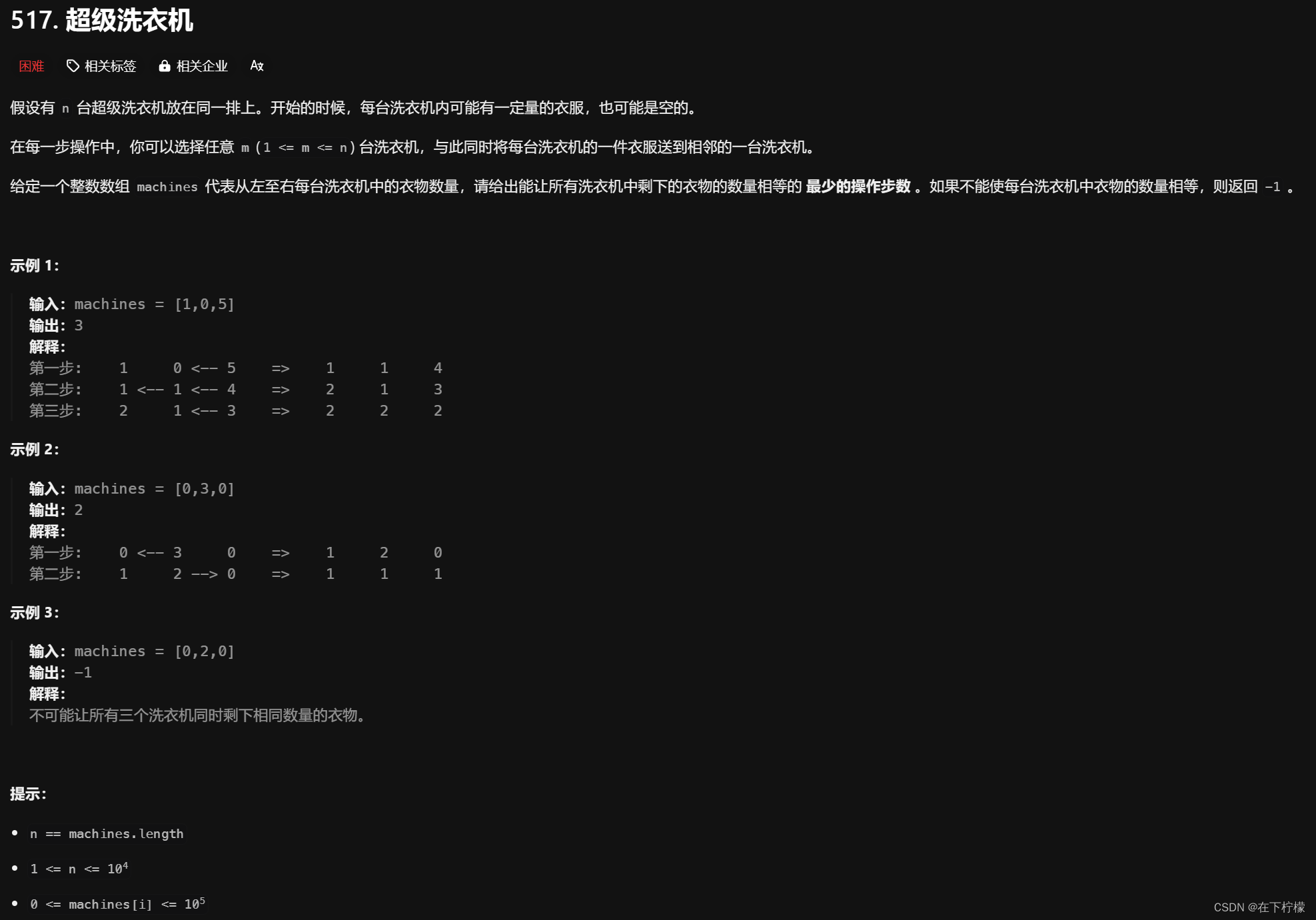
- 每次可以选n/2对洗衣机传值,但是如果中间有0分割,就不能这么算,例如[0,0,11,5]
func findMinMoves(nums []int) (res int) {// 每次最多选n/2对洗衣机转移1件衣物,但是如果有0把数组分成若干份,那不能联通// [0, 0, 11, 5]=>[4, 4, 4, 4],二者做差,得到[-4, -4, 7, 1]// 对于第一个洗衣机来说,需要四件衣服可以从第二个洗衣机获得// 那么就可以把-4移给二号洗衣机,那么差值数组变为[0, -8, 7, 1]// 此时二号洗衣机需要八件衣服,从三号洗衣机处获得,那么差值数组变为[0, 0, -1, 1]// 此时三号洗衣机还缺1件,就从四号洗衣机处获得,变为[0, 0, 0, 0]// 过程中差值最大数是8,即需要8次操作次数n := len(nums)sum := 0for _,x := range nums{sum += x}if sum%n!=0{return -1}avg := sum/n// 计算差值,同时找出最大操作次数,这个操作次数可能是差值7,也可能是传导过程中的-8// 注意,差值也可能有-9,但是负数是要传导的,可能-9两边都是正数,一轮可以传导2个// 所以比较差值时不用abs,比较传导值时要abs// 有一个问题,传导的方向是遍历的方向,如果例子[0,0,11,5]改成[5,11,0,0]或者[5,11,0,0,0,55,111]是否也成立?// 也成立,抽象成正->负->正,遍历过程累加的正值需要若干次操作次数传至负,而累加出现负说明左边尽力之后需要右边正传值,所以向左右传值的顺序是不影响最终结果的conduct := 0for _,x := range nums{x -= avgconduct += xres = max(res, max(x, abs(conduct)))}return res
}
func abs(x int)int{if x<0{return -x}else{return x}}
8、Dijkstra
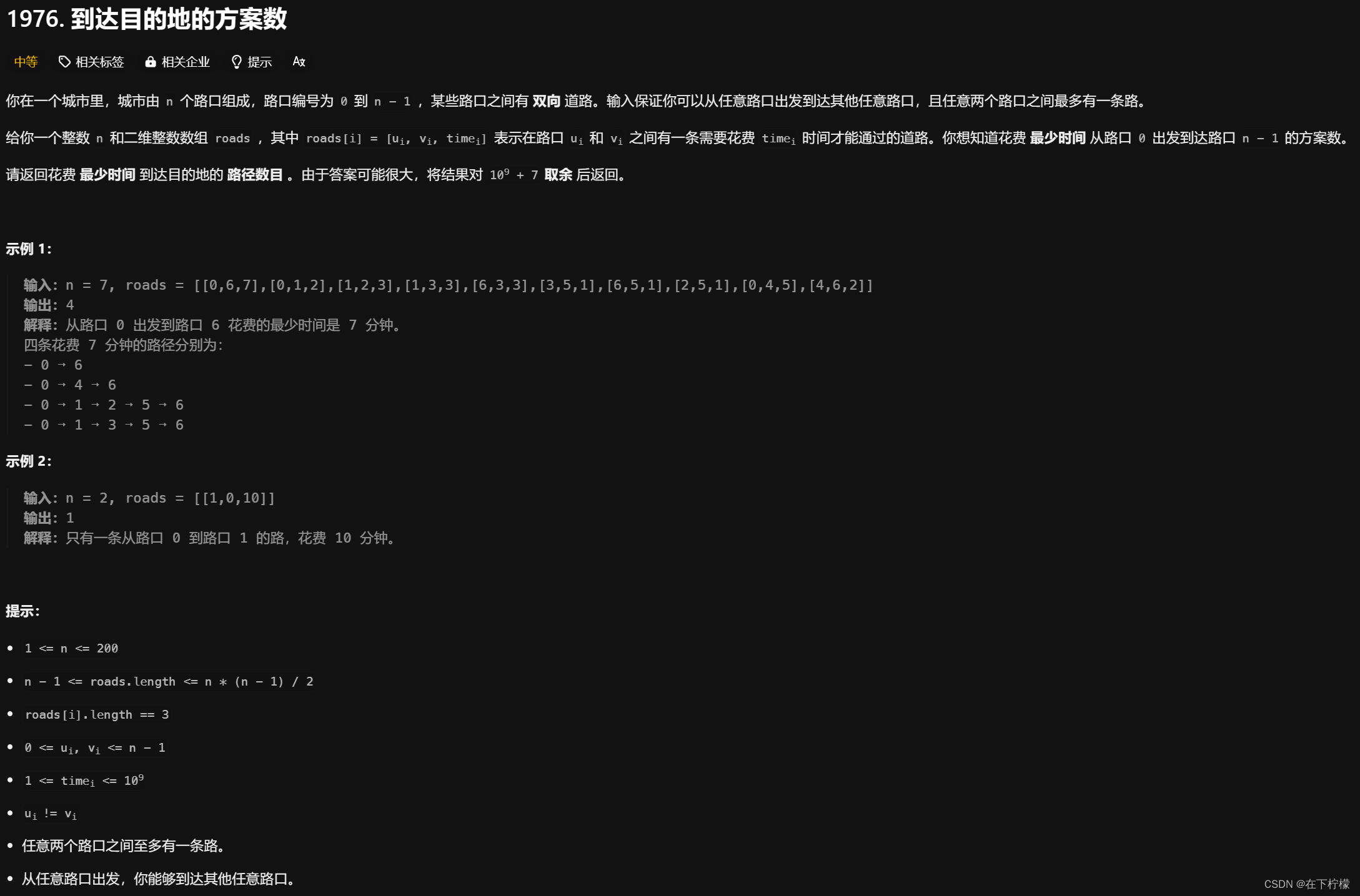
- 求0到n-1的最短路径的方案数,Dijkstra,在更新最短距离时记录可能中间节点k的个数,例如示例一,0->6的中间节点有0/4/5,5的中间节点有0/2/3。
func countPaths(n int, roads [][]int) int {// dijkstra,计算固定i到任意j最短距离// 每轮选择i到其他点的最短距离,用这个点当中间节点更新i到其他点最短距离,依此类推// dijkstra的关键三步骤是建图g、最短距离dis、寻找中间节点0->k->iMOD := int(1e9)+7g := make([][]int,n)for i := range g{g[i] = make([]int,n)for j := range g[i]{g[i][j] = math.MaxInt/2}}for _,arr := range roads{x,y,v := arr[0],arr[1],arr[2]g[x][y] = vg[y][x] = v}// 0->i的最短距离dis := make([]int, n)for i := 1; i < n; i++ {dis[i] = math.MaxInt / 2}// 每轮更新距离时,如果0->k->i比0->i短,即找到更短的一种方案,赋值dp[k]给dp[i],相等就累加// 初始化,0->0只有一种方案dp := make([]int,n)dp[0] = 1// 每个点是否成为过最短距离点vis := make([]bool,n)for {// 寻找未遍历过0->k的最小值,这个寻找最小值的过程可以用堆优化k,minn := -1,math.MaxIntfor i,x := range dis{if x<minn && !vis[i]{k = iminn = x}}if k==-1{// 遍历结束break}vis[k] = truefor i,x := range g[k]{// 0->k->inewDis := dis[k]+xif newDis<dis[i]{dis[i] = newDisdp[i] = dp[k]}else if newDis==dis[i]{dp[i] = (dp[i]+dp[k])%MOD}}}return dp[n-1]
}
9、背包问题,01背包和完全背包
01背包指只有若干的同一种的物品,每次可以选也可以不选,能否凑出价值target
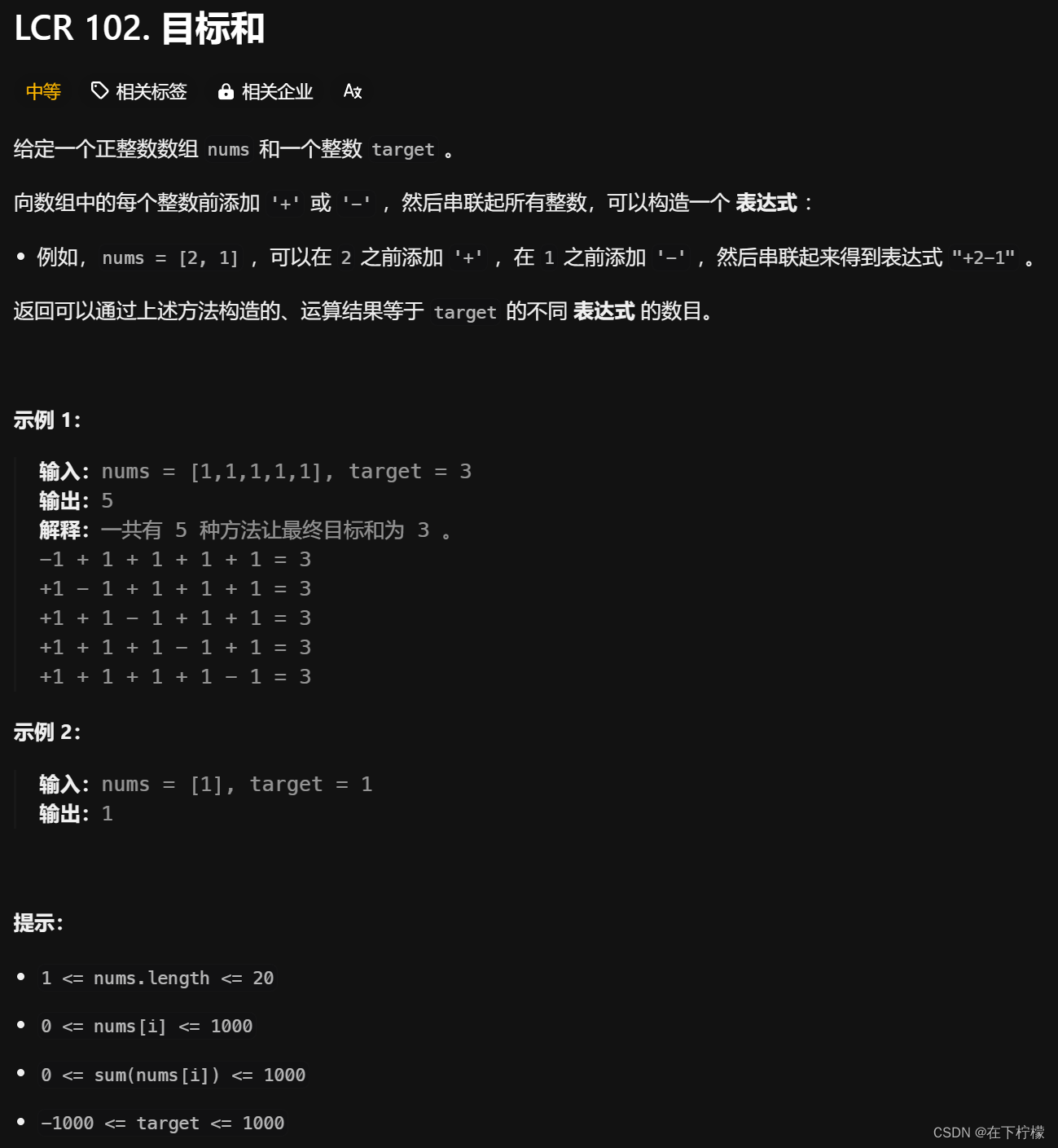
- 假设正数p,负数q,p-q=sum,p+q=target,2p=sum+target,也就是说,选择若干个数字,使得其和等于(sum+target)/2,其中物品没有种类的概念,每个物品只有价值的区分,可以选或不选,即为01背包问题
- 下面的代码从dfs到动态规划,再到状态压缩
class Solution {public int findTargetSumWays(int[] nums, int target) {// 假设正数p,负数q,p-q=sum,p+q=target,2p=sum+target// 也就是说,选择若干个数字,使得其和等于(sum+target)/2// 01背包问题,也是动态规化,选则容量减少,不选则容量不变// 递归到子问题就是前i-1个数选若干个使得容量为更新后的容量int sum = 0;for (int x : nums){sum += x;}if ((sum+target)%2==1){// 奇数,理论上没有解return 0;}// 前n个数,选择若干个数组成target,01背包问题,动态规划int n = nums.length;target = (sum+target)/2;// dfs// dp[i][j]表示前i个数组成j,有几种方法int[][] dp = new int[n+1][target+1];public int dfs(int i, int cap, int[]nums, int[][] dp){if (i==-1){if (cap==0){return 1;}return 0;}if (dp[i][cap]!=0){return dp[i][cap];}if (cap<nums[i]){// 只能不选dp[i][cap] = dfs(i-1,cap,nums,dp);return dp[i][cap];}dp[i][cap] = dfs(i-1,cap-nums[i],nums,dp)+dfs(i-1,cap,nums,dp);return dp[i][cap];}return dfs(n-1,target,nums,dp);// 把记忆化搜索改成递推// 初始化条件,当i=0,j=0,dp[i][j]=1int[][] dp = new int[n+1][target+1];dp[0][0] = 1;for (int i=0;i<n;i++){int x = nums[i];for (int cap=0;cap<=target;cap++){if (cap>=x){// 可以选dp[i+1][cap] = dp[i][cap]+dp[i][cap-x];}else{// 不可以选dp[i+1][cap] = dp[i][cap];}}}return dp[n][target];// 是否能进行空间上的优化,每个i只使用到i-1的数据int[] dp = new int[target+1];dp[0] = 1;for (int x : nums){// 此时需要逆序计算,否则后面cap-x时取到前面的值已经更新成i的了,而非i-1for (int cap = target;cap>=x;cap--){dp[cap] += dp[cap-x];}}return dp[target];}
}
完全背包问题是有若干种不同的物品,每个物品有不同的重量wi和价值vi,每种物品可以选择任意次,在选择小于等于target的物品的情况下,求选择的最大价值和

- 每种金币有不同的金额和个数,且可以选择无数次,要求选择金额在amount的情况下,求最小的选择个数,这就是完全背包问题
- 同样从dfs到动态规划,再到压缩dp解题
class Solution {public int coinChange(int[] coins, int amount) {// 完全背包问题// 第i种物品有体积wi和价值vi,每种物品可以选择无限个,在总体积限制条件下,求能选择的最大价值// 与01背包最大的不同是,选择一种物品后,还可以继续选,而不是递归到下一个i-1int n = coins.length;// dfs,dp[i][j]表示前i个物品选j总重情况下的最小硬币数int[][] dp = new int[n][amount+1];// 返回最少硬币数public int dfs(int i, int sum, int[] nums, int[][] dp){if (i==-1){if (sum==0){// 是一种合法的方案return 0;}return Integer.MAX_VALUE/2;}if (dp[i][sum]!=0){return dp[i][sum];}// 只能不选if (nums[i]>sum){dp[i][sum] = dfs(i-1,sum,nums,dp);return dp[i][sum];}// 可以选,也可以不选// 注意,每件物品可以选任意次,所以即使选了,往下递归的还是idp[i][sum] = Math.min(dfs(i-1,sum,nums,dp), dfs(i,sum-nums[i],nums,dp)+1);return dp[i][sum];}int cnt = dfs(n-1,amount,coins,dp);return cnt<Integer.MAX_VALUE/2 ? cnt : -1;// 动态规划int[][] dp = new int[n+1][amount+1];// 初始化,由于取最小的硬币数,所以全是MAX,而dp[0][0]=0Arrays.fill(dp[0], Integer.MAX_VALUE/2);dp[0][0] = 0;for (int i=0;i<n;i++){int x = coins[i];for (int cap=0;cap<=amount;cap++){if (cap<x){dp[i+1][cap] = dp[i][cap];}else{dp[i+1][cap] = Math.min(dp[i][cap], dp[i+1][cap-x]+1);}}}return dp[n][amount]<Integer.MAX_VALUE/2 ? dp[n][amount] : -1;// 空间优化int[] dp = new int[amount+1];Arrays.fill(dp, Integer.MAX_VALUE/2);dp[0] = 0;for (int x : coins){// 这里无需逆序,因为取x后需要i的cap-x,而前面正好更新过了for (int cap=x;cap<=amount;cap++){dp[cap] = Math.min(dp[cap], dp[cap-x]+1);}}return dp[amount]<Integer.MAX_VALUE/2 ? dp[amount] : -1;}
}
从nums中选出一些数字使其组合为n
func change(n int, nums []int) int {dp := make([]int,n+1)dp[0] = 1// nums每个数可以选任意次for _,x := range nums{for i := range dp{if i-x>=0{dp[i] += dp[i-x]}}}// nums中每个数只能选一次for _,x := range nums{for i:=n-1;i>=0;i--{if i-x>=0{dp[i] += dp[i-x]}}}// i的每种组合是有顺序的,例如6=1+2+3=3+2+1是两种答案for i := range dp{for _,x := range nums{if i-x>=0{dp[i] += dp[i-x]}}}return dp[n]
}
10、矩阵生成未被选过的随机点

-
建立一个一维数组,数组中保存0~nm-1的下标,每次从未抽到的下标中随机选一个,与尾部交换并抛出,从而保证数组中有num个0
-
但是这么做m*n超内存,可以用map只记录选过的位置
-
每次随机的数如果没选过,那就在前num个数中,就是0,直接转换
-
如果选过了,那map中映射的value是剩余0的个数,即num,用value转换
-
最后更新选择的数字映射为num,如果num已经被用过了,就映射为num的映射物上
-
总而言之,map中的key是1,value以及没被记录的是0,而num只记录剩余0的个数,如果当前num没有被使用,那就保存在value中
type Solution struct {Map map[int]intNum intN intM int
}func Constructor(m int, n int) Solution {// 建立一个一维数组,数组中保存0~n*m-1的下标,每次从未抽到的下标中随机选一个,与尾部交换并抛出,从而保证数组中有num个0// 但是这么做m*n超内存,可以用map只记录选过的位置// 每次随机的数如果没选过,那就在前num个数中,就是0,直接转换// 如果选过了,那map中映射的value是剩余0的个数,即num,用value转换// 最后更新选择的数字映射为num,如果num已经被用过了,就映射为num的映射物上// 总而言之,map中的key是1,value以及没被记录的是0,而num只记录剩余0的个数,如果当前num没有被使用,那就保存在value中return Solution{map[int]int{},m*n,m,n}
}func (this *Solution) Flip() (res []int) {m := this.Mx := rand.Intn(this.Num)this.Num--if v,ok:=this.Map[x];ok{// 已经用过x了res = []int{v/m, v%m}}else{res = []int{x/m, x%m}}if v,ok:=this.Map[this.Num];ok{// num这个数被用过,那x不能映射到num上,可以映射到num映射的数上this.Map[x] = v}else{this.Map[x] = this.Num}return
}func (this *Solution) Reset() {this.Num = this.N*this.Mthis.Map = map[int]int{}return
}/*** Your Solution object will be instantiated and called as such:* obj := Constructor(m, n);* param_1 := obj.Flip();* obj.Reset();*/
11、寻找符合要求的矩形区域
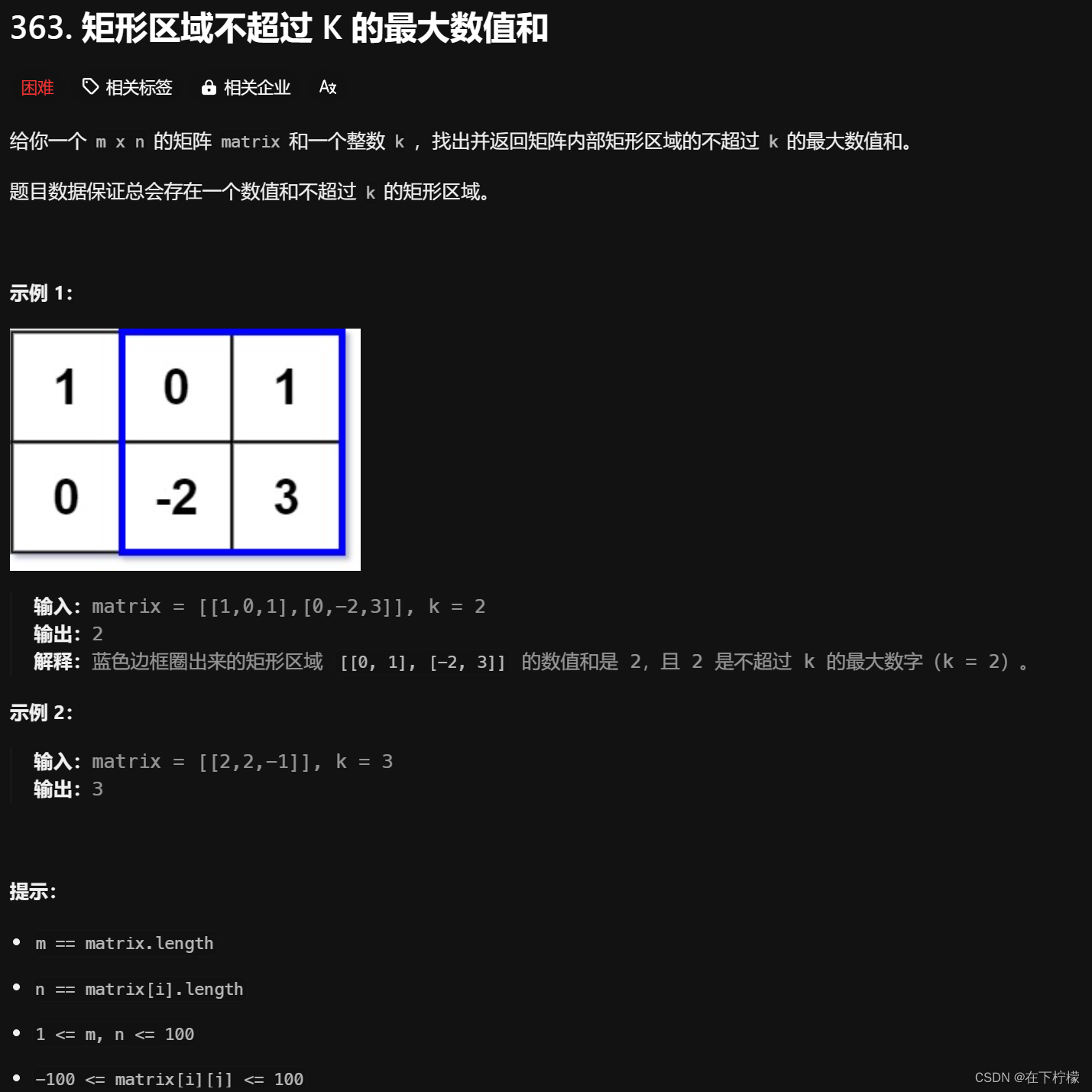
-
**进阶:**如果行数远大于列数,该如何设计解决方案?
-
一眼前缀和,但是如何遍历,总不能O(n2m2)复杂度吧
-
矩形有四个边,枚举左右两条边,在左右边固定的条件下,计算每一行的总和,得到一列数组,求前缀和,二重遍历枚举矩形的面积,如果面积小于等于k,就与维护的最大值进行比较,最后返回最大值
-
这种固定左右两条边,每一行累加,按列求前缀和的思路比较新颖
func maxSumSubmatrix(matrix [][]int, k int) int {// 枚举左右边界,在左右边界确定的情况下,计算每一行的总和,找到最大的一段连续数组// 这个思路对进阶问题同样有效,行数远大于列数,枚举左右边界次数更少n,m := len(matrix),len(matrix[0])nums := make([][]int,n)for i,arr := range matrix{// 相比matrix,nums每一行多了一个前导0,便于计算前缀和nums[i] = make([]int,m+1)for j,x := range arr{// 每一行求前缀和,用于后续计算nums[i][j+1] = nums[i][j]+x}}res := math.MinIntfor l:=0;l<m;l++{for r:=l;r<m;r++{// 在[l,r]中累加每一行的总和,前缀和nums[i][r+1]-nums[i][l]// 用dp计算最大连续子数组的和,dp[i]=max(dp[i-1]+x, x)// 也可以直接用pre代替dp[i-1]// 注意:计算过程中大于k的区间和不做保存,只比较小于等于k的pre := make([]int,n+1)maxn := math.MinIntfor i:=0;i<n;i++{pre[i+1] = pre[i]+(nums[i][r+1]-nums[i][l])// i-j遍历所有子数组for j:=0;j<=i;j++{sum := pre[i+1]-pre[j]if sum<=k && sum>maxn{maxn = sum}}}// fmt.Println(l,r,maxn,pre)res = max(res, maxn)}}return res
}
12、找出第k大的子序列和

-
所有正数的和是最大的子序列和,通过删正数或加负数,即减去绝对值来得到更小的子序列和
-
得到sum和绝对值之后有两种思路求第k大子序列和
-
第一个思路,求第k小子序列的和,然后用sum减去,[0,所有绝对值的和]二分结果,选或不选递归查找,如果有至少k种组合得到mid,或当前sum+遍历的nums[i]>mid,就是偏大了,不够k种就是偏小
-
第二个思路,求第k小子序列的和,初始化最小堆中装入(0,0),即(sum,i+1),抛出k-1次最小值,将nums[i+1]加入sum,或者替换sum中的nums[i],最后sum减去堆顶最小值元素
func kSum(nums []int, k int) int64 {// 所有正数的和是最大的子序列和,通过删正数或加负数,即减去绝对值来得到更小的子序列和// 得到sum和绝对值之后有两种思路求第k大子序列和// 第一个思路,求第k小子序列的和,然后用sum减去,[0,所有绝对值的和]二分结果,// 选或不选递归查找,如果有至少k种组合得到mid,或当前sum+遍历的nums[i]>mid,就是偏大了,不够k种就是偏小// 第二个思路,求第k小子序列的和,初始化最小堆中装入(0,0),即(sum,i+1)// 抛出k-1次最小值,将nums[i+1]加入sum,或者替换sum中的nums[i],最后sum减去堆顶最小值元素sum := 0sumDel := 0for i,x := range nums{if x>=0{sum += xsumDel += x}else{nums[i] = -xsumDel += -x}}sort.Ints(nums)n := len(nums)// 二分查找第k小的子序列和del := sort.Search(sumDel,func(m int)bool{// 是否有k个子序列的和小于等于m// 空子序列也算一种组合,表示一个不选,加快运算速度cnt := 1var dfs func(int,int)dfs = func(i,sum int){if i==n || cnt==k || sum+nums[i]>m{// 遍历结束,或已经有有k种组合,或后续sum过大可以剪枝操作return}// 选cnt++dfs(i+1,sum+nums[i])// 不选,此处不加一,全部不选的1在开头加过了dfs(i+1,sum)}dfs(0,0)return cnt==k})return int64(sum-del)
}
13、从nums中选k个不相交子数组,使得总能量最大
-
划分型dp,dp[i][j]表示前j个数字划分成i段,前len(nums)个数划分成k段
-
一般做法:
-
不选nums[j],前j个数划分成i段,即
dp[i][j] = dp[i][j-1] -
选nums[j],
dp[i][j] = dp[i-1][k]+strength(k+1,j),strength为能量值 -
能量值的计算是k个子数组和乘上权重值w,子数组和用前缀和求,权重=k-i
-
枚举i,j,k,初始化
dp[0][j]=0,dp[i][]=-inf,最终返回dp[k][n] -
复杂度O(n2k)=1e10,超时!
-
如何优化?
-
上述
dp[i][j] = max{dp[i][j-1], maxk{dp[i-1][k]+(s[j]-s[k])*wi}}
= max{ ... , s[j]*wi + maxk{dp[i-1][k]-s[k]*wi}} -
把max中第二项和j有关的因子提出来,发现是一个固定的值,而剩下和i,k有关项随j的增加只会增加一个
-
分析k的变化范围:
for i in (1,k+1):划分段数for j in (i,n):最后一个元素下标for k in (i-1,j):最后一个子数组前一个元素,最低i-1表示前i-1段只有一个元素,最高j-1表示最后一个子数组只有一个元素 -
对于每轮i,j,max(k)的计算只需要比较前一项和增加的项,从而O(1)完成,复杂度降为O(n2)=1e8
-
综上:
dp[i][j] = max{dp[i][j-1], s[j]*wi + maxn}maxn = maxk{dp[i-1][k]-s[k]*wi}
/**
划分型dp,dp[i][j]表示前j个数字划分成i段,前len(nums)个数划分成k段
一般做法:
不选nums[j],前j个数划分成i段,即dp[i][j] = dp[i][j-1]
选nums[j],dp[i][j] = dp[i-1][k]+strength(k+1,j),strength为能量值
能量值的计算是k个子数组和乘上权重值w,子数组和用前缀和求,权重=k-i
枚举i,j,k,初始化dp[0][j]=0,dp[i][<i]=-inf,最终返回dp[k][n]
复杂度O(n2k)=1e10,超时!如何优化?
上述dp[i][j] = max{dp[i][j-1], maxk{dp[i-1][k]+(s[j]-s[k])*wi}}= max{ ... , s[j]*wi + maxk{dp[i-1][k]-s[k]*wi}}
把max中第二项和j有关的因子提出来,发现是一个固定的值,而剩下和i,k有关项随j的增加只会增加一个
分析k的变化范围:
for i in (1,k+1):划分段数
for j in (i,n):最后一个元素下标
for k in (i-1,j):最后一个子数组前一个元素,最低i-1表示前i-1段只有一个元素,最高j-1表示最后一个子数组只有一个元素
对于每轮i,j,max(k)的计算只需要比较前一项和增加的项,从而O(1)完成综上:
dp[i][j] = max{dp[i][j-1], s[j]*wi + maxn}
maxn = maxk{dp[i-1][k]-s[k]*wi}
**/
func maximumStrength(nums []int, k int) int64 {n := len(nums)dp := make([][]int,k+1)for i := range dp{dp[i] = make([]int,n+1)// 初始化for j:=0;j<i;j++{dp[i][j] = math.MinInt}}// 前缀和,加一个前置0s := make([]int,n+1)for i,x := range nums{s[i+1] += s[i]+x}// 二重遍历for i:=1;i<=k;i++{// 计算能量值的系数wi := k-i+1if i%2==0{wi = -wi}// 初始化maxnmaxn := math.MinInt// 枚举最后一个子数组的最后一个元素// 当前第i组,前面至少留i-1个元素,后面至少留k-i个元素,即n-k+ifor j:=i;j<=n-k+i;j++{// 更新maxnmaxn = max(maxn, dp[i-1][j-1]-s[j-1]*wi)dp[i][j] = max(dp[i][j-1], s[j]*wi+maxn)}}return int64(dp[k][n])
}
14、加密解密,全局ID生成器
- 为URL分一个独有的ID,ID和URL作为键值对装入map中,最后返回加密的结果
- 生成ID的方法有,自增数字ID、随机生成、哈希生成
type Codec struct {S stringPrefix stringCnt map[string]string
}func Constructor() Codec {return Codec{"0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ","http://tinyurl.com/",map[string]string{}}
}// Encodes a URL to a shortened URL.
func (this *Codec) encode(longUrl string) string {// 返回的加密URL=前缀+6个字符的随机字符串,装入map中,用于解密// 除了随机生成,还可以用自增ID,哈希生成等方法// 哈希生成,将URL每个字符乘上一个质数,求和,与另一个质数求余,结果作为key,例如1117和1e9+7suff := strings.Builder{}for i:=0;i<6;i++{suff.WriteByte(this.S[rand.Intn(len(this.S))])}tinyUrl := this.Prefix+suff.String()this.Cnt[tinyUrl] = longUrlreturn tinyUrl
}// Decodes a shortened URL to its original URL.
func (this *Codec) decode(shortUrl string) string {return this.Cnt[shortUrl]
}/*** Your Codec object will be instantiated and called as such:* obj := Constructor();* url := obj.encode(longUrl);* ans := obj.decode(url);*/
15、多种情况的动态规化如何做

- 首先要能看出是动态规化,其次
dp[i][j][k]表示三种情况,这三种情况是第i天的三种情况,即出勤,缺勤天数,连续迟到天数,对这种状态应当分类讨论,从而确定dp[i]的各个情况
func checkRecord(n int) int {// 动态规划,dp[i][j][k]表示出勤P:i天,缺勤A:j次,已连续迟到L:k天// 缺勤之前只能不缺勤了,不缺勤之前无限制// 连续迟到k次的前一次连续迟到k-1次,0次之前无限制MOD := int(1e9)+7dp := make([][2][3]int,n+1)dp[0][0][0] = 1for i:=1;i<n+1;i++{// 以P结尾的数量,即出勤for j:=0;j<2;j++{for k:=0;k<3;k++{dp[i][j][0] = (dp[i][j][0] + dp[i-1][j][k]) % MOD}}// 以A结尾的数量,即缺勤for k:=0;k<3;k++{dp[i][1][0] = (dp[i][1][0] + dp[i-1][0][k]) % MOD}// 以L结尾的数量,即迟到for j:=0;j<2;j++{for k:=1;k<3;k++{dp[i][j][k] = (dp[i][j][k] + dp[i-1][j][k-1]) % MOD}}}sum := 0for j:=0;j<2;j++{for k:=0;k<3;k++{sum = (sum + dp[n][j][k])%MOD}}return sum
}
16、多种情况的动态规化如何做2

- 给出若干种长宽的木块,求最大值
dp[i][j]表示高 i 宽 j 的木块最多卖多少钱- 一共有三种情况,直接卖,竖着切,横着切,取三种情况最大值
func sellingWood(m int, n int, prices [][]int) int64 {// dp[i][j]表示高i宽j的木块最多卖多少钱// 三种情况,直接卖,竖着切,横着切,取三种情况最大值dp := make([][]int,m+1)for i := range dp{dp[i] = make([]int,n+1)}// 对价格建图price := make([][]int,m+1)for i := range price{price[i] = make([]int,n+1)}for _,arr := range prices{x,y,v := arr[0],arr[1],arr[2]price[x][y] = v}// 动态规划for i:=1;i<=m;i++{for j:=1;j<=n;j++{// 直接卖dp[i][j] = price[i][j]// 枚举竖着切的情况for k:=1;k<j;k++{dp[i][j] = max(dp[i][j], dp[i][k]+dp[i][j-k])}// 枚举横着切的情况for k:=1;k<i;k++{dp[i][j] = max(dp[i][j], dp[k][j]+dp[i-k][j])}}}return int64(dp[m][n])
}
17、查找n最近的回文数

- 很难的题目,让我知道有一些题就是没有一本万利的解法,就是会有一些特殊情况
- 前半部分为num,num、num+1、num-1对称,注意如果是奇数不能对称前n/2个数
- 特殊例子:11、个位数、若干个9、10的幂,分别返回9,-1,+2,-1
func nearestPalindromic(s string) string {// 前半部分为num,num、num+1、num-1对称,注意如果是奇数不能对称前n/2个数// 特殊例子:11、个位数、若干个9、10的幂if s=="11"{return "9"}n := len(s)num,_ := strconv.Atoi(s)if n==1{return strconv.Itoa(num-1)}if only9(s){return strconv.Itoa(num+2)}if is10(s){return strconv.Itoa(num-1)}// num对称s1 := s[:(n+1)/2]+reverse(s[:n/2])num1,_ := strconv.Atoi(s1)// 注意题目要求不等于num,而只有num对称可能等于原值if num1==num{num1 = math.MaxInt}// +1-1对称,如果若干个9不在前面排除,这里会导致进位增加判断量// 例如999,res=1001,但是截取前半段对称结果是10001或100001// 如果不是全9,那结果只能在num/num+1/num-1对称这三个结果中num0,_ := strconv.Atoi(s[:(n+1)/2])s2 := strconv.Itoa(num0+1)if n%2==0{s2 += reverse(s2)}else{s2 += reverse(s2[:n/2])}num2,_ := strconv.Atoi(s2)s3 := strconv.Itoa(num0-1)if n%2==0{s3 += reverse(s3)}else{s3 += reverse(s3[:n/2])}num3,_ := strconv.Atoi(s3)// 从num1/num2/num3中选一个离num最近的数,从小到大num3/num1/num2// fmt.Println(num,num1,num2,num3)if abs(num3-num)<=abs(num1-num) && abs(num3-num)<=abs(num2-num){return s3}if abs(num1-num)<=abs(num2-num) && abs(num1-num)<=abs(num3-num){return s1}if abs(num2-num)<abs(num1-num) && abs(num2-num)<abs(num3-num){return s2}return "#"
}
func reverse(s string)string{arr := []byte(s)n := len(arr)for i:=0;i<n/2;i++{arr[i],arr[n-1-i] = arr[n-1-i],arr[i]}return string(arr)
}
func only9(s string)bool{for i := range s{if s[i]!='9'{return false}}return true
}
func is10(s string)bool{if s[0]=='1'{if v,_:=strconv.Atoi(s[1:]);v==0{return true}}return false
}
func abs(x int)int{if x<0{return -x}else{return x}}
最后欣赏一下超简洁的Python代码
class Solution:def nearestPalindromic(self, n: str) -> str:if int(n)<10 or int(n[::-1])==1:return str(int(n)-1)if n=='11':return '9'if set(n)=={'9'}:return str(int(n)+2)a,b=n[:(len(n)+1)//2],n[(len(n)+1)//2:]temp=[str(int(a)-1),a,str(int(a)+1)]temp=[i+i[len(b)-1::-1] for i in temp]return min(temp,key=lambda x:abs(int(x)-int(n)) or float('inf'))
18、分数最少,且字典序最小
- 这道题该如何思考呢?想要分数最小,得尽可能的让所有字符出现次数一致,如果能根据出现频率和字典序排序的最小堆,然后把所有字符排序,再填入s,即可
- 首先统计s中已经出现的次数
- 其次有几个?就循环几次,把堆顶字母加入一个数组中
- 最后对字母排序,字典序最小,填入字符串s中
- 注意:Python的最小堆按照第一维和第二维排序
class Solution:def minimizeStringValue(self, s: str) -> str:# 尽可能的让所有字符出现次数一致# 首先统计s中已经出现的次数# 其次有几个?就循环几次,把堆顶字母加入一个数组中# 最后对字母排序,字典序最小,填入字符串s中# 注意:Python的最小堆按照第一维和第二维排序freq = Counter(s)q = [(freq[chr(c)],chr(c)) for c in range(ord('a'),ord('z')+1)]heapify(q)t = []for _ in range(freq['?']):f,c = heappop(q)t.append(c)heappush(q,(f+1,c))t.sort()s = list(s)idx = 0for i in range(len(s)):if s[i]=='?':s[i] = t[idx]idx += 1return ''.join(s)
加下来看看Java中对堆的处理
class Solution {public String minimizeStringValue(String S) {// 尽可能的让所有字符出现次数一致// 首先统计s中已经出现的次数// 其次有几个?就循环几次,把堆顶字母加入一个数组中// 最后对字母排序,字典序最小,填入字符串s中char[] s = S.toCharArray();int[] freq = new int[26];// 问号的个数int num = 0;for (char c : s){if (c=='?'){num++;}else{freq[c-'a']++;}}// 最小堆PriorityQueue<Pair<Integer,Character>> q = new PriorityQueue<>(26, (x,y) -> {// 排序,频率小 || 频率同且字典序小int diff = x.getKey().compareTo(y.getKey());return diff!=0 ? diff : x.getValue().compareTo(y.getValue());});for (char c='a'; c<='z'; c++){q.add(new Pair<>(freq[c-'a'], c));}// 循环?次char[] t = new char[num];for (int i=0;i<num;i++){Pair<Integer,Character> temp = q.poll();char c = temp.getValue();t[i] = c;q.add(new Pair<>(temp.getKey()+1, c));}Arrays.sort(t);// 填充字符for (int i=0,j=0;i<s.length;i++){if (s[i]=='?'){s[i] = t[j++];}}return new String(s);}
}
19、删除元素,使其出现频率满足要求

-
这道题的思路也很巧妙,枚举出现次数最少的字符数num,小于num的全删除,大于num的最多保留num+k
-
统计保留字符数求和结果sum,返回n-sum
func minimumDeletions(word string, k int) int {// 枚举出现次数最少的字符数cnt,小于cnt的全删除,大于cnt的最多保留cnt+k// 统计保留字符数求和结果sum,返回n-sumn := len(word)cnt := make([]int,26)for i := range word{cnt[int(word[i]-'a')]++}sort.Ints(cnt)// 维护最大保留字符数的可能sum := -1for i,minn := range cnt{temp := 0for _,v := range cnt[i:]{temp += min(v,minn+k)}sum = max(sum,temp)}return n-sum
}
20、max(区间最小值*区间长度)

- 这道题如果试图从k往两边走,同时维护区间内最小值,每轮走的情况有三种,左走、右走、两边走,这种思路是错误的,走的方向实际上可以用两个方向的值来判断,哪个值更大,就走哪个方向
- 用两个指针从k出发,哪个更大就移动那个指针,直到[0,n],更新res和min。
- 为什么这种走法正确呢?假设最终结果[l,r]内最小值min,那l-1和r+1要么是左右边界,要么比min小。
- 为什么边界值一定比区间内最小值要小呢?反证法,如果比min还要大或相等,那更大范围和更大最小值乘积肯定更大,[l,r]还可以外扩。
- 除了双指针,还可以用单调栈,找区间内最小值比较困难,那就反过来把每个nums[i]当成区间内最小值,nums[i]的区间长度就是左右两边第一个小于nums[i]的下标的差,这个区间长度可以用单调递增栈来计算,有点类似最大矩形面积那道题
- 如果计算的区间范围包括k,就更新res
func maximumScore(nums []int, k int) int {// 单调栈// 找区间内最小值困难,反过来每个nums[i]的区间长度左右两边第一个小于nums[i]的下标差// 当计算的区间范围包括k时,更新res,用单调递增栈计算区间范围n := len(nums)q := make([]int,0,n)q = append(q,-1)res := -1for i,x := range nums{for len(q)>1 && nums[q[len(q)-1]]>=x{if i>k && k>q[len(q)-2]{res = max(res, nums[q[len(q)-1]]*(i-q[len(q)-2]-1))}// fmt.Println(nums[q[len(q)-1]],q[len(q)-2]+1,i-1)q = q[:len(q)-1]}q = append(q,i)}// 清空单调栈q内残余值for len(q)>1{if k>q[len(q)-2]{res = max(res, nums[q[len(q)-1]]*(n-q[len(q)-2]-1))}// fmt.Println(nums[q[len(q)-1]],q[len(q)-2]+1,i-1)q = q[:len(q)-1]}return res// 双指针// 假设最终结果[l,r]内最小值min,那l-1和r+1要么是左右边界,要么比min小// 反证法,如果比min还要大,那更大范围和更大最小值乘积肯定更大,[l,r]还可以外扩// 用两个指针从k出发,哪个更大就移动那个指针,直到[0,n],更新res和minn := len(nums)l,r := k,kminn := nums[k]res := nums[k]// on没有意义,只是表示最多遍历n-1次for on:=0;on<n-1;on++{// l左移if r==n-1 || (l>0 && nums[l-1]>nums[r+1]){l--minn = min(minn, nums[l])}else{// r右移r++minn = min(minn, nums[r])}res = max(res, minn*(r-l+1))}return res
}
21、从示例中找规律

- 根据第三个示例,猜测规律,
mul(1~7) = 7*(1,6)*(2,5)*(3,4) = 7*1*6*1*6*1*6 = 7*(7-1)^(7/2)
func minNonZeroProduct(p int) int {// 当两数之差最大时,乘积最小,所以最小数是1,其他位都给别的数使其变大// 根据第三个例子,sum(1,7)=7*(1+6)*(2+5)*(3+4)=7*1*6*1*6*1*6// 猜测res=max*(max-1)^(n/2),其中max=2^p-1,n=2^p-1MOD := int(1e9)+7pow := func(x,n int)int{res := 1for n>0{if n%2==1{res = res*x%MOD}x = x*x%MODn /= 2}return res}// 这里注意不能用pow计算,因为算出来的是MOD之后的结果,在下面计算幂运算出错maxn := 1<<p-1return maxn%MOD * pow((maxn-1)%MOD, (maxn-1)/2)%MOD
}
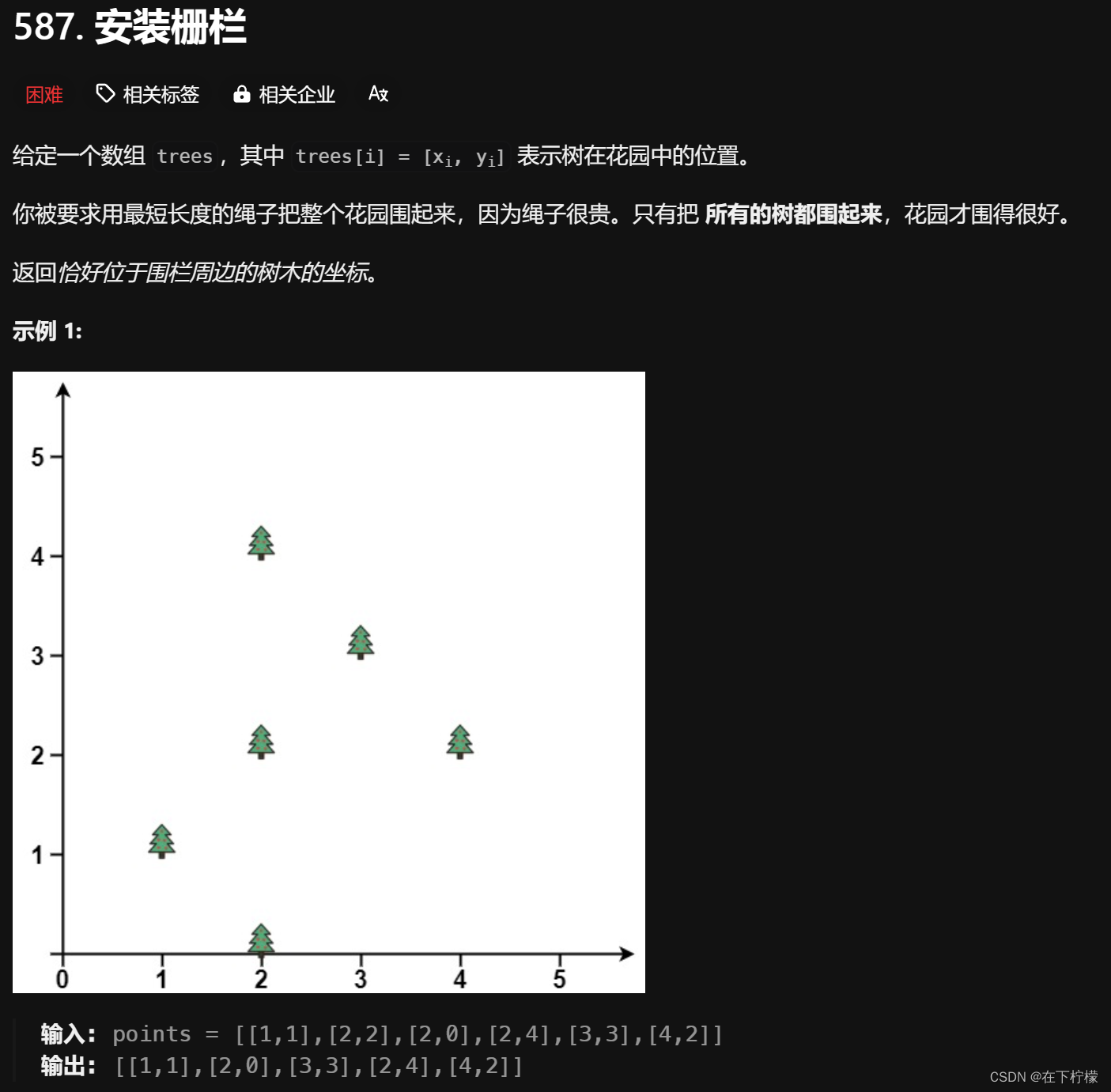
22、凸包问题——Andrew算法
- 这道题是凸包问题,对应的算法很多,这里选择较为简单的Andrew算法
- Andrew算法,把整个边界分成上下两个凸包处理
- 根据x和y排序,首先处理上凸包,从前往后装入两个点
- 第三个点如果在前两点组成的线左边,∠312>0,说明点3在上凸包上面,保留3,删2
- 如果第三个点在右边,∠312<0,保留3和2,2和3组成新的线,计算点4,依此类推,下凸包同理
- 遍历一遍,点1会入栈两次,分别作为上凸起点和下凸终点,所以最终返回栈前n-1个元素
func outerTrees(nums [][]int) [][]int {// 凸包问题,Andrew算法,把整个边界分成上下两个凸包处理// 根据x和y排序,首先处理上凸包,从前往后装入两个点// 第三个点如果在前两点组成的线左边,∠312>0,说明点3在上凸包上面,保留3,删2// 如果第三个点在右边,∠312<0,保留3和2,2和3组成新的线,计算点4// 遍历一遍点1会入栈两次,分别作为上凸起点和下凸终点,所以最终返回栈前n-1个元素,下凸包同理n := len(nums)if n<4{return nums}sort.SliceStable(nums, func(i,j int)bool{return nums[i][0]<nums[j][0] || (nums[i][0]==nums[j][0] && nums[i][1]<nums[j][1])})// 只记录下标,最后整理数据格式并返回q := make([]int, 0, n)idx := 0vis := make([]bool, n)// 通过计算两个向量ab,ac面积,来表示∠bac大小cal := func(i,j,k int)int{a,b,c := nums[i],nums[j],nums[k]ab := []int{b[0]-a[0], b[1]-a[1]}ac := []int{c[0]-a[0], c[1]-a[1]}// 叉乘bac := ab[0]*ac[1]-ab[1]*ac[0]return bac}// 上凸包for i:=0;i<n;i++{// 注意,加3删2的过程是循环执行的,直到点3不是上凸包的上边界的点for idx>=2{// 通过计算两个向量ab,ac的面积,来判断∠bac的大小,正数加c删b,负数加cif cal(q[idx-2],q[idx-1],i)>0{// 删bvis[q[idx-1]] = falseq = q[:idx-1]idx--}else{break}}// 加cvis[i] = trueq = append(q, i)idx++}// 上凸包的终点,就是下凸包的起点flag := idx// 同理,下凸包的终点就是上凸包的起点,所以需要把起点重新标记为未遍历vis[0] = falsefor i:=n-1;i>=0;i--{if vis[i]{// 属于上凸包的,就不是下凸包,无需遍历continue}// 这里注意,无需新增两个点作为初始值,因为作为上凸包,其他点只能在下面for idx>=flag{if cal(q[idx-2],q[idx-1],i)>0{// 删b,这一步的标记已经没有必要了,对了对称才写的vis[q[idx-1]] = falseq = q[:idx-1]idx--}else{break}}// 加cq = append(q, i)idx++vis[i] = true}res := make([][]int,len(q)-1)for i,j := range q[:len(q)-1]{res[i] = nums[j]}return res
}
23、从左上角到右下角的最小步数

- 这道题注意数据范围,直接广度优先遍历的复杂度是1e5*1e5超时
- 正确解法是动态规化+每一行每一列最小堆,对于
dp[i][j],指从左上角到当前位置的最小步数,而遍历过的,即左上角区域,都计算好了dp,如果对从行和列抵达i,j进行最小堆维护,就可以O(1)的查找最小步数,最小堆中以dp[i][j]作为排序标准,第二个维度是行或列,因为还要判断,从i1,j或i,j1是否能抵达i,j,如果不能,就抛出,如果栈空,就说明这个点无法到达,不入栈
class Solution {public int minimumVisitedCells(int[][] grid) {// 常规广度优先遍历在最后几个用例超时,本题动态规化+每一行每一列优先队列// dp[i][j]表示从0,0到i,j所需最小步数,最后返回dp[n-1][m-1]// 对于每个i,j,左上角都是计算好的dp,考虑从i1,j或i,j1抵达i,j// 每一行和每一列维护一个优先队列,从而O(1)的查找抵达i,j的最小步数// 如果不能抵达,就抛出,如果行的队列为空,说明从行走到不了i,j,行和列都为空,那这个点不作考虑int n = grid.length, m = grid[0].length;int[][] dp = new int[n][m];for (int i=0;i<n;i++){Arrays.fill(dp[i], Integer.MAX_VALUE/2);}// 初始化dp[0][0] = 1;// 行和列的优先队列数组,都是最小堆PriorityQueue<int[]>[] row = new PriorityQueue[n];PriorityQueue<int[]>[] col = new PriorityQueue[m];// 最小堆中装入的是(步数, 行或列)// 如果从行i1到达i,那装入列最小堆,反之亦然for (int i=0;i<n;i++){row[i] = new PriorityQueue<>((a,b) -> a[0]-b[0]);}for (int i=0;i<m;i++){col[i] = new PriorityQueue<>((a,b) -> a[0]-b[0]);}// 二重遍历for (int i=0;i<n;i++){for (int j=0;j<m;j++){// 不断检查堆顶元素,如果无法到达i,j就抛出,更新dp// 从列抵达,行的最小堆while (!row[i].isEmpty() && row[i].peek()[1]+grid[i][row[i].peek()[1]]<j){row[i].poll();}if (!row[i].isEmpty()){dp[i][j] = Math.min(dp[i][j], dp[i][row[i].peek()[1]]+1);}// 从行抵达,列的最小堆while (!col[j].isEmpty() && col[j].peek()[1]+grid[col[j].peek()[1]][j]<i){col[j].poll();}if (!col[j].isEmpty()){dp[i][j] = Math.min(dp[i][j], dp[col[j].peek()[1]][j]+1);}// 更新最小堆if (dp[i][j] != Integer.MAX_VALUE/2){row[i].offer(new int[]{dp[i][j], j});col[j].offer(new int[]{dp[i][j], i});}}}return dp[n-1][m-1]!=Integer.MAX_VALUE/2 ? dp[n-1][m-1] : -1;}
}
24、判断四个点是否是正方形

- 第一个思路,如果两条斜边中点相同,且长度相同,且相互垂直,就说明这两条斜边组成一个正方形
- 第二个思路,如果四个点围绕中心旋转90度仍然在四个点的坐标中,就说明是个正方形,这个要提前计算中点,并根据中点进行坐标偏移,90度旋转公式:x,y -> -y,x
- 第三个思路,以第一个点为原点,检查剩下三个点形成向量是否垂直,长度是否相同
25、最大的频率
- 如果频率不变,那直接最大堆返回堆顶元素,但是需要动态改变堆内频率值
- 注意到每个值对应唯一的频率,用map维护真正的值-频率,如果堆顶的值对应频率不一致,就抛出
- 总结,用Map维护正确的值-频率,用堆进行排序,维护堆顶元素正确性,最大堆+lazy延迟删除
class Solution {public long[] mostFrequentIDs(int[] nums, int[] freq) {// 返回最大的频率,用最大堆维护频率,返回堆顶元素// 但是这样做没办法O(1)的修改频率,无论是增加还是删除// 注意到每个值对应唯一的频率,用map维护真正的值-频率,如果堆顶的值对应频率不一致,就抛出// 总结,用Map维护正确的值-频率,用堆进行排序,维护堆顶元素正确性// freq需要用long类型,注意数据结构PriorityQueue<Pair<Integer,Long>> q = new PriorityQueue<>((a,b) -> {// (x,freq),按照第二个维度递减排序return Long.compare(b.getValue(),a.getValue());});Map<Integer,Long> cnt = new HashMap<>();int n = nums.length;long[] res = new long[n];for (int i=0;i<n;i++){int x=nums[i];long f=freq[i];cnt.merge(x, f, Long::sum);q.add(new Pair<>(x, cnt.get(x)));while (!q.peek().getValue().equals(cnt.get(q.peek().getKey()))){q.poll();}res[i] = q.peek().getValue();}return res;}
}
26、最长公共后缀,字典树

-
返回t在s中对应下标,要求公共后缀最长,s长度最短,下标最靠前
-
字典树tire,对s进行预处理,全部加入到tree中,每个节点维护(minLen,minIdx)
-
例如示例1,倒着加入tree:
-
加入abcd,d(4,0),c(4,0),b(4,0),a(4,0) ->
-
加入bcd,d(3,1),c(3,1),b(3,1),a(4,0) ->
-
加入xbcd,d(3,1),c(3,1),b(3,1),a(4,0)&x(4,2)
-
-
查询时倒着查询,直到查不到了,就是最长公共后缀
-
注意字典树的头需要加一个空字符串,表示没有匹配上公共后缀的情况
func stringIndices(s []string, t []string) []int {// 返回t在s中对应下标,要求公共后缀最长,s长度最短,下标最靠前// 字典树tire,对s进行预处理,全部加入到tree中,每个节点维护(minLen,minIdx)// 例如示例1,倒着加入tree// 加入abcd,d(4,0),c(4,0),b(4,0),a(4,0) -> // 加入bcd,d(3,1),c(3,1),b(3,1),a(4,0) -> // 加入xbcd,d(3,1),c(3,1),b(3,1),a(4,0)&x(4,2)// 查询时倒着查询,直到查不到了,就是最长公共后缀// 注意字典树的头需要加一个空字符串,表示没有匹配上公共后缀的情况// 字典树Tire,每个节点包括26的数组,和(minLen,minIdx),提供添加和查询方法type Node struct{nums [26]*NodeminL intminI int}root := &Node{[26]*Node{},math.MaxInt,0}// 添加for i,x := range s{l := len(x)// 添加字符串xcur := root// 空字符串,不用考虑字符charif l<cur.minL{cur.minL,cur.minI = l,i}// 因为匹配后缀,所以倒着遍历for j:=l-1;j>=0;j--{c := x[j]-'a'if cur.nums[c]==nil{cur.nums[c] = &Node{[26]*Node{},math.MaxInt,0}}cur = cur.nums[c]if l<cur.minL{cur.minL,cur.minI = l,i}}}// 查询res := make([]int,len(t))for i,x := range t{cur := rootfor i:=len(x)-1;i>=0 && cur.nums[x[i]-'a']!=nil;i--{cur = cur.nums[x[i]-'a']}res[i] = cur.minI}return res
}
补充Java字典树的写法
class Node{Node[] nums = new Node[26];int minL = Integer.MAX_VALUE;int minI = 0;
}
class Solution {public int[] stringIndices(String[] wordsContainer, String[] wordsQuery) {// 创建字典树Node root = new Node();// 添加for (int i=0;i<wordsContainer.length;i++){char[] s = wordsContainer[i].toCharArray();int l = s.length;Node cur = root;if (l<cur.minL){cur.minL = l;cur.minI = i;}for (int j=l-1;j>=0;j--){int c = s[j]-'a';if (cur.nums[c]==null){cur.nums[c] = new Node();}cur = cur.nums[c];if (l<cur.minL){cur.minL = l;cur.minI = i;}}}// 查询int[] res = new int[wordsQuery.length];for (int i=0;i<wordsQuery.length;i++){char[] s = wordsQuery[i].toCharArray();Node cur = root;for (int j=s.length-1;j>=0 && cur.nums[s[j]-'a']!=null;j--){cur = cur.nums[s[j]-'a'];}res[i] = cur.minI;}return res;}
}class Node{Node[] nums = new Node[26];int minL = Integer.MAX_VALUE;int minI = 0;
}
class Solution {public int[] stringIndices(String[] wordsContainer, String[] wordsQuery) {// 创建字典树Node root = new Node();// 添加for (int i=0;i<wordsContainer.length;i++){char[] s = wordsContainer[i].toCharArray();int l = s.length;Node cur = root;if (l<cur.minL){cur.minL = l;cur.minI = i;}for (int j=l-1;j>=0;j--){int c = s[j]-'a';if (cur.nums[c]==null){cur.nums[c] = new Node();}cur = cur.nums[c];if (l<cur.minL){cur.minL = l;cur.minI = i;}}}// 查询int[] res = new int[wordsQuery.length];for (int i=0;i<wordsQuery.length;i++){char[] s = wordsQuery[i].toCharArray();Node cur = root;for (int j=s.length-1;j>=0 && cur.nums[s[j]-'a']!=null;j--){cur = cur.nums[s[j]-'a'];}res[i] = cur.minI;}return res;}
}
27、二维接雨水
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。

- 一维数组每个点的边界是min(前后缀最大值),二维数组每个点的边界是min(围成圈的木板)
- 将最外围的点加入最小堆,每个堆顶最小值是上下左右没有被遍历过点的最短木板,更新这个点的接水量,并加入最小堆
class Solution {public int trapRainWater(int[][] heightMap) {// 一维数组每个点的边界是min(前后缀最大值),二维数组每个点的边界是min(一圈)// 将最外围的点加入最小堆,每个堆顶最小值是上下左右没有被遍历过点的最短木板,更新这个点的接水量,并加入最小堆int n=heightMap.length, m=heightMap[0].length;boolean[] vis = new boolean[n*m];PriorityQueue<Pair<Integer,Integer>> pq = new PriorityQueue<>((a,b) -> {// (装水后的高度, x*n+y),第一维度递增return a.getKey().compareTo(b.getKey());});for (int i=0;i<n;i++){for (int j=0;j<m;j++){if (i==0 || i==n-1 || j==0 || j==m-1){vis[i*m+j] = true;pq.add(new Pair<>(heightMap[i][j], i*m+j));}}}int res = 0;// 注意这种枚举上下左右的方式int[] d = {-1, 0, 1, 0, -1};while (!pq.isEmpty()){Pair<Integer,Integer> p = pq.poll();int h = p.getKey(), idx = p.getValue();for (int i=0;i<4;i++){int x = idx/m + d[i];int y = idx%m + d[i+1];if (x>=0 && x<n && y>=0 && y<m && !vis[x*m+y]){res += Math.max(0, h-heightMap[x][y]);vis[x*m+y] = true;pq.add(new Pair<>(Math.max(heightMap[x][y],h),x*m+y));}}}return res;}
}
28、三指针,固定其一,相向移动其二

- 常规排序后三重遍历i<=j<=k,这种做法实际是固定两条边找第三条边
- 固定一条边,找两条边,例如固定k,如果i+j>k,那i或j增加的所有情况都成立,减少的情况都不成立
- 那这样将i从小到大,j从大到小相向移动,大于k,res+=j-i,小于k,continue
func triangleNumber(nums []int) int {// 常规排序后三重遍历i<=j<=k,这种做法实际是固定两条边找第三条边// 固定一条边,找两条边,例如固定k,如果i+j>k,那i或j增加的所有情况都成立,减少的情况都不成立// 那这样将i从小到大,j从大到小相向移动,大于k,res+=j-i,小于k,continuen := len(nums)sort.Ints(nums)res := 0for k:=2;k<n;k++{i,j := 0,k-1for i<j{if nums[i]+nums[j]>nums[k]{res += j-ij--}else{i++}}}return res
}
29、相同任务之间须有间隔,求最短完成时间
- 这道题相同任务之间需要至少间隔n,例如A->…n…->A,完成时间是n+2,求最少完成的总时间
- 如果统计每个任务个数,从大到小遍历,对每个字符个数mi计算
mi*(n+1)-n是行不通的 - 有两种可能的意外,字符太少不够填充n,字符太多需要往后接若干个长度
- 那从大到小遍历,每个字符的时间片个数是m,最优情况是
m*(n+1)-n,即A->X->X->A->X->X->A - 往后遍历m1,m1<=m,如果小于m,直接填充到m个时间片内,如果大于m,那最后一个时间片往后接1,即
A->B->X->A->B->X->A->B - 如果把
m*(n+1)-n个空格都填满了,那无需往后接若干个长度,而是在每个时间片后接,因为每个时间片的间隔大于等于n,够mi用 - 不过计算出m的最优情况后无需填充空格,因为最后的结果要么是空格没占满,要么占满还往后接,答案为
max(m*(n+1)-n+x,len),x是mi=m的情况个数
func leastInterval(tasks []byte, n int) int {// 统计每个任务个数,从大到小遍历,对每个个数计算m*(n+1)-n是行不通的// 有两种可能的意外,字符太少不够填充n,字符太多需要往后接若干个长度// 那从大到小遍历,每个字符的时间片个数是m,最优情况是m*(n+1)-n,即A->X->X->A->X->X->A// 往后遍历m1,m1<=m,如果小于m,直接填充到m个时间片内,如果大于m,那最后一个时间片往后接1,即A->B->X->A->B->X->A->B// 如果把m*(n+1)-n个空格都填满了,那无需往后接若干个长度,而是在每个时间片后接,因为每个时间片的间隔大于等于n,够mi用// 不过计算出m的最优情况后无需填充空格,因为最后的结果要么是空格没占满,要么占满还往后接,答案为max(m*(n+1)-n+x,len),x是mi=m的情况个数nums := make([]int,26)for _,c := range tasks{nums[int(c-'A')]++}sort.Sort(sort.Reverse(sort.IntSlice(nums)))m := nums[0]res := m*(n+1)-nfor _,mi := range nums[1:]{if mi==m{res++}}return max(res,len(tasks))
}
30、循环队列如何判断null和full
- 假设循环队列队首和队尾指针分别是front和rear。当队列为空,可知front=rear;而当所有队列空间全占满时,也有 front=rear。无法区分这两种情况
- 可以把队列长度设为cap+1,只允许装入cap个元素,而两个指针的变化范围是[0, cap],当
front=rear,表示队列已满,当循环队列中只剩下一个空存储单元时,即front==(rear+1)%n,则表示队列已满。
// 假设队列使用的数组有capacity个存储空间,则此时规定循环队列最多只能有capacity−1个队列元素
// 当循环队列中只剩下一个空存储单元时,则表示队列已满。
public boolean isEmpty() {// 保证l和r在[0,n-1]之内return l==r;
}public boolean isFull() {// 如果l==0,r==n-1,那已经存满了,r+1%n = 0 = lreturn l==(r+1)%n;
}
31、Dijkstra设计题

-
本题比较常规,通过Dijkstra或Floyd找最短路径,但是其中的设计思路和细节还是要注意
-
思路一,每次找start->end的最短路径,用Dijkstra算法,由于首尾两点都是确定的,所以可用最小堆优化
-
思路二,初始化直接Dijkstra计算所有最短路径,每次addEdge时,如果大于等于计算出的路径,直接return
,如果小于,那以i->x->y->j的所有ij都需要更新,使用Floyd更新
思路一:
class Graph {// 1、每次找start->end的最短路径,用Dijkstra算法,由于首尾两点都是确定的,所以可用最小堆优化// 2、初始化直接Dijkstra计算所有最短路径,每次addEdge时,如果大于等于计算出的路径,直接return// 如果小于,那以i->x->y->j的所有ij都需要更新private static final int INF = Integer.MAX_VALUE/2;private final List<int[]>[] nums;int n;public Graph(int n, int[][] edges) {this.n = n;nums = new ArrayList[n];Arrays.setAll(nums, i -> new ArrayList<>());for (int[] e : edges) {nums[e[0]].add(new int[]{e[1], e[2]});}}public void addEdge(int[] edge) {nums[edge[0]].add(new int[]{edge[1],edge[2]});}public int shortestPath(int start, int end) {// 查找从start到end的最短路径,dis[i]表示start->i的最短路径int[] dis = new int[n];Arrays.fill(dis, INF);dis[start] = 0;// 最小堆装入(dis[j],j),每次取出最小的dis,更新j->k,直到堆为空PriorityQueue<int[]> q = new PriorityQueue<>((a,b) -> (a[0]-b[0]));q.offer(new int[]{0,start});while (!q.isEmpty()){int[] temp = q.poll();int d = temp[0];int i = temp[1];if (i==end){break;}if (d>dis[i]){// dis[i]被更新过,说明之前遍历过i,直接continue,这样不用viscontinue;}for (int[] a : this.nums[i]){if (d+a[1]<dis[a[0]]){dis[a[0]] = d+a[1];q.offer(new int[]{dis[a[0]],a[0]});}}}return dis[end]==INF ? -1 : dis[end];}
}
思路二:
class Graph {// 1、每次找start->end的最短路径,用Dijkstra算法,由于首尾两点都是确定的,所以可用最小堆优化// 2、初始化直接Dijkstra计算所有最短路径,每次addEdge时,如果大于等于计算出的路径,直接return// 如果小于,那以i->x->y->j的所有ij都需要更新// 由于Floyd存在n1+v+n2的操作,所以初始化最大值要除3private static final int INF = Integer.MAX_VALUE/3;private final int[][] nums;int n;public Graph(int n, int[][] edges) {this.n = n;nums = new int[n][n];for (int i=0;i<n;i++){Arrays.fill(nums[i], INF);nums[i][i] = 0;}for (int[] a : edges){nums[a[0]][a[1]] = a[2];}// dijkstrafor (int k=0;k<n;k++){for (int i=0;i<n;i++){if (nums[i][k]==INF){continue;}for (int j=0;j<n;j++){nums[i][j] = Math.min(nums[i][j], nums[i][k]+nums[k][j]);}}}}public void addEdge(int[] edge) {int x=edge[0], y=edge[1], v=edge[2];if (v>=nums[x][y]){return;}// floydfor (int i=0;i<n;i++){for (int j=0;j<n;j++){nums[i][j] = Math.min(nums[i][j], nums[i][x]+v+nums[y][j]);}}}public int shortestPath(int start, int end) {return nums[start][end]>=INF ? -1 : nums[start][end];}
}
32、从俩数组挑选n种元素

- 从两个数组中各取n/2个数,使得n个数种类最多,假设共有m种元素,独有m1,m2种元素
- 挑选的角度,优先从独有中选元素,k1=min(m1,n/2),k2=min(m2,n/2)
- 因为k1+k2<=n,所以可以从共有中选min(m,n-k1-k2)
- 删除的角度过于复杂,先删除重复元素,然后从交集中删,最后从独有中删
func maximumSetSize(nums1 []int, nums2 []int) int {// 从两个数组中各取n/2个数,使得n个数种类最多,假设共有m种元素,独有m1,m2种元素// 挑选的角度,优先从独有中选元素,k1=min(m1,n/2),k2=min(m2,n/2)// 因为k1+k2<=n,所以可以从共有中选min(m,n-k1-k2)// 删除的角度过于复杂,先删除重复元素,然后从交集中删,最后从独有中删n := len(nums1)cnt1 := map[int]int{}for _,x := range nums1{cnt1[x]++}cnt2 := map[int]int{}for _,x := range nums2{cnt2[x]++}m := 0for k := range cnt1{if _,ok:=cnt2[k];ok{m++}}m1 := len(cnt1)-mm2 := len(cnt2)-mk1 := min(m1, n/2)k2 := min(m2, n/2)k := min(m, n-k1-k2)return k+k1+k2
}
33、一次跳跃的线性遍历,dp+前缀和

- dp,dp[i]是从0到i的步数,第n-1位置只需计算第一次到的步数
- 第一次到j所用步数
dp[j-1]+1,然后跳到小于j的i - 第二次到j,即从i回到j,即从i回到j-1再到j,所需步数
dp[j-1]-dp[i]+1 - 两者相加就是从0到j的步数
func firstDayBeenInAllRooms(nextVisit []int) int {// dp,dp[i]是从0到i的步数,第n-1位置只需计算第一次到的步数// 第一次到j所用步数=dp[j-1]+1,然后跳到小于j的i// 第二次到j,即从i回到j,即从i回到j-1再到j,所需步数=dp[j-1]-dp[i]+1// 两者相加就是从0到j的步数MOD := int(1e9)+7n := len(nextVisit)dp := make([]int,n+1)// 初始化,到0用0天,到-1用-1天dp[0] = -1for j,i := range nextVisit{if j<n-1{// 有时候算出负数未必是越界,也可能是相减得负数dp[j+1] = ((dp[j]+1) + (dp[j]-dp[i]+1+MOD))%MOD}else{dp[j+1] = (dp[j]+1)%MOD}}return dp[n]
}
34、从每个数组中选一个数组成最小区间
- 最小堆+贪心
- 从每个数组中选一个数,使得min(最大值-最小值)
- 用最小堆维护最小值,同时维护最大值,如果最小值对应数组遍历到头了,就return
class Solution {public int[] smallestRange(List<List<Integer>> nums) {// 最小堆+贪心// 从每个数组中选一个数,使得min(最大值-最小值)// 用最小堆维护最小值,同时维护最大值,如果最小值对应数组遍历到头了,就returnPriorityQueue<int[]> q = new PriorityQueue<>((a,b) -> {// 最小堆装入(x,xi,i),以第一维度升序排序return a[0]-b[0];});int maxn = Integer.MIN_VALUE;// 初始化for (int i=0;i<nums.size();i++){int x = nums.get(i).get(0);q.add(new int[]{x,0,i});maxn = Math.max(maxn,x);}int[] res = new int[]{(int)-1e5,(int)1e5};while (true){int[] a = q.poll();if (maxn-a[0]<res[1]-res[0]){res = new int[]{a[0],maxn};}// 如果堆顶元素已经遍历完了,就returnif (a[1]==nums.get(a[2]).size()-1){return res;}a[1]++;a[0] = nums.get(a[2]).get(a[1]);q.add(a);maxn = Math.max(maxn,a[0]);}}
}
35、最大或值,最短长度的子数组
- 遍历i,以i为左边界的子数组[i,j],有最大的or值和最小的长度j-i+1,暴力超时
- 优化,遍历j,每个j对于每个i只有三种可能,[i,j],[i…j…k],要么在区间外[i,k]…j
- 前两种都需要or到nums[i]上,最后一种不用,又由于or有单增不减的性质,如果当前i不需要j,那前面的i在经过[i,k]后也不需要j,所以从j-1倒着遍历i
- 如果or的值不变,说明[i,k]不包含j,而i之前的or上[i,k]也不需要j,直接break
- 如果or的值变大了就说明j在区间内,要么是边界要么是内部,反正都需要or上,更新nums[i],
- 这样优化,每次第二重遍历不会超过二进制位数,即2^30,时间复杂度O(30*n)
class Solution {public int[] smallestSubarrays1(int[] nums) {// 遍历i,以i为左边界的子数组[i,j],有最大的or值和最小的长度j-i+1,暴力超时// 优化,遍历j,每个j对于每个i只有三种可能,[i,j],[i..j..k],要么在区间外[i,k]..j// 前两种都需要or到nums[i]上,最后一种不用,又由于or有单增不减的性质,如果当前i不需要j,那前面的i在经过[i,k]后也不需要j,所以从j-1倒着遍历i// 如果or的值不变,说明[i,k]不包含j,而i之前的or上[i,k]也不需要j,直接break// 如果or的值变大了就说明j在区间内,要么是边界要么是内部,反正都需要or上,更新nums[i],// 这样优化,每次第二重遍历不会超过二进制位数,即2^30,时间复杂度O(30*n)int n = nums.length;int[] res = new int[n];Arrays.fill(res,1);for (int j=0;j<n;j++){for (int i=j-1;i>=0 && nums[i]!=(nums[i]|nums[j]);i--){nums[i] |= nums[j];res[i] = j-i+1;}}return res;}
- or具有单增不减的性质,数据范围2^30,那最多能单增30次
- 如果用二维数组记录or的值和j,倒着遍历i,nums[i]与记录的or值相或,数组下标0的元素就是最大or值和对应的最小j
- 如何保证or值最大?or单增不减,如何保证j最小?每次将nums[i]或完,相同or值合并,保留最小j
- 这个模板可以求出所有子数组按位或的结果,以及or值等于k的最小j和最大j,把j换成cnt,还可以记录个数
class Solution {public int[] smallestSubarrays(int[] nums) {// or具有单增不减的性质,数据范围2^30,那最多能单增30次// 如果用二维数组记录or的值和j,倒着遍历i,nums[i]与记录的or值相或,数组下标0的元素就是最大or值和对应的最小j// 如何保证or值最大?or单增不减,如何保证j最小?每次将nums[i]或完,相同or值合并,保留最小j// 这个模板可以求出所有子数组按位或的结果,以及or值等于k的最小j和最大j,把j换成cnt,还可以记录个数int n = nums.length;int[] res = new int[n];List<int[]> q = new ArrayList<>();for (int i=n-1;i>=0;i--){// 加入自己q.add(new int[]{0,i});// 原地去重,双指针int k = 0;// 将nums[i]与nums[j]的or值相或for (int[] a : q){a[0] |= nums[i];if (q.get(k)[0]==a[0]){// 合并,保留最小的jq.get(k)[1] = a[1];}else{// 无需合并,由于or的单增性,所以a[0]不可能比k之前的值还要大,直接覆盖k++;q.set(k,a);}}// 删除k之后的点q.subList(k+1,q.size()).clear();res[i] = q.get(0)[1]-i+1;}return res;}
}
36、删除一个点后最小的最大曼哈顿距离
- 曼哈顿距离(x1,y1)->(x2,y2) = |x1-x2|+|y1-y2| = max(|x1’-x2’|, |y1’-y2’|),其中(x’, y’) = (x+y, y-x)
- 要求最大距离,用有序数组记录x’和y’,max-min即可,要求最小的,枚举所有数被删除后的值,求个min
class Solution {public int minimumDistance(int[][] points) {// 曼哈顿距离(x1,y1)->(x2,y2) = |x1-x2|+|y1-y2| = max(|x1'-x2'|, |y1'-y2'|)// 其中(x', y') = (x+y, y-x)// 要求最大距离,用有序数组记录x'和y',max-min即可,所有数被删除的值求个min// 有序数组TreeMap,加入x自动从小到大排序TreeMap<Integer,Integer> xs = new TreeMap<>();TreeMap<Integer,Integer> ys = new TreeMap<>();for (int[] a : points){int x=a[0], y=a[1];xs.merge(x+y, 1, Integer::sum);ys.merge(y-x, 1, Integer::sum);}int res = Integer.MAX_VALUE;for (int[] a : points){int x=a[0]+a[1], y=a[1]-a[0];// 删除这个点if (xs.get(x)==1) xs.remove(x);else xs.merge(x, -1, Integer::sum);if (ys.get(y)==1) ys.remove(y);else ys.merge(y, -1, Integer::sum);// 计算res,min(res, max-min)res = Math.min(res, Math.max(xs.lastKey()-xs.firstKey(), ys.lastKey()-ys.firstKey()));// 重新加入这个点xs.merge(x, 1, Integer::sum);ys.merge(y, 1, Integer::sum);}return res;}
}
37、双指针找链表环形,以及环形的首

- 快慢双指针找环,如果快指针先跑到null,就没环
- 若有环,两者必在环上相遇,此时重置fast为head,且一步一步移动
- 当fast移动到环的首部时,slow也移动到这里了
public class Solution {public ListNode detectCycle(ListNode head) {// 快慢双指针找环,如果快指针先跑到null,就没环// 若有环,两者必在环上相遇,此时重置fast为head,且一步一步移动// 当fast移动到环的首部时,slow也移动到这里了if (head==null || head.next==null){return null;}ListNode fast=head,slow=head;while (fast!=null && fast.next!=null){slow = slow.next;fast = fast.next.next;if (fast==slow){break;}}if (fast!=slow){// 是因为fast跑到头才退出的,returnreturn null;}fast = head;while (fast!=slow){fast = fast.next;slow = slow.next;}return slow;}
}
38、可以组成排序二叉树的数组

- 最初的想法是root+左+右,以及root+右+左,但是看下面这个例子
[2,1,4,null,null,3],组成它的数组中有一个是[2,4,1,3],左子节点居然插在右子节点中间- 实际上只要左右子树内部的相对顺序不变,两个子树是可以交叉的,那组合的唯一判断标准就是根节点是否在子节点之前,所以递归回溯,每次从备选节点中选一个加入数组,将左右子节点加入备选节点
- 例如上个例子,加入2后有1,4,加入4后有1,3,加入1后有3,加入3后备选为空,直接加入res即可
class Solution {List<List<Integer>> res;public List<List<Integer>> BSTSequences(TreeNode root) {res = new ArrayList();if (root==null){res.add(new ArrayList());return res;}List<Integer> list = new ArrayList();list.add(root.val);List<TreeNode> next = new ArrayList();if (root.left!=null){next.add(root.left);}if (root.right!=null){next.add(root.right);}dfs(list, next);return res;}void dfs(List<Integer> list, List<TreeNode> next){// 尝试从next选一个加入List,如果next为空,就加入到res中if (next.isEmpty()){res.add(new ArrayList<>(list));}for (int i=0;i<next.size();i++){TreeNode node = next.get(i);List<Integer> t1 = new ArrayList<>(list);t1.add(node.val);List<TreeNode> t2 = new ArrayList<>(next);t2.remove(i);if (node.left!=null){t2.add(node.left);}if (node.right!=null){t2.add(node.right);}dfs(t1,t2);}}
}
39、第k个祖先
- 一般解法是一步步往上跳,
node = parent[node],但是超时 - 如果我预处理每个节点的第2个祖先节点,那就可以两步两步往上跳,时间复杂度减半
- 预处理每个节点的第2^i个祖先节点,k=13=8+4+1,只需三次即可算出结果
- 预处理的结果放在
fa[idx][i],初始化fa[idx][0]=parent[idx],跳2^0=1步 - x的第16个祖先是x的第8个祖先的第8个祖先,所以
fa[idx][i] = fa[ fa[idx][i-1] ][i-1]
class TreeAncestor {// 一般解法是一步步往上跳,node = parent[node]// 如果我预处理每个节点的第2个祖先节点,那就可以两步两步往上跳,时间复杂度减半// 预处理每个节点的第2^i个祖先节点,k=13=8+4+1,只需三次即可算出结果// 预处理的结果放在fa[idx][i],初始化fa[idx][0]=parent[idx],跳2^0=1步// x的第16个祖先是x的第8个祖先的第8个祖先,所以fa[idx][i] = fa[ fa[idx][i-1] ][i-1]int[][] fa;public TreeAncestor(int n, int[] parent) {// 通过最大的idx,即n,来计算2^i中i的最大值mint m = 32-Integer.numberOfLeadingZeros(n);fa = new int[n][m];for (int idx=0;idx<n;idx++) fa[idx][0] = parent[idx];for (int i=1;i<m;i++){for (int idx=0;idx<n;idx++){int f = fa[idx][i-1];fa[idx][i] = f==-1 ? -1 : fa[f][i-1];}}}public int getKthAncestor(int node, int k) {// 将k分解成二进制,每次获取最低位1的位数,即lowbit(1)=>2^iwhile (k>0 && node!=-1){node = fa[node][Integer.numberOfTrailingZeros(k)];k &= k-1;}return node;}
}
40、位运算求相同数目1的略大和略小的数
- 变大:最后一个01变为10,后续1右靠,未找到01返回-1
- num加上最低位1,即可完成01->10,并清空末尾连续1,取反与num相与即可截取末尾连续1,右移或上即可
- 变小:最后一个10变为01,后续1左靠,未找到10返回-1
- 或者,按位取反,变大,然后按位取反
class Solution {public int[] findClosedNumbers(int num) {// 变大:最后一个01变为10,后续1右靠,未找到01返回-1// num加上最低位1,即可完成01->10,并清空末尾连续1,取反与num相与即可截取末尾连续1,右移或上即可// 变小:最后一个10变为01,后续1左靠,未找到10返回-1// 或者,按位取反,变大,然后按位取反int[] res = new int[]{calMax(num), ~calMax(~num)};if (res[0]<=0) res[0] = -1;if (res[1]<=0) res[1] = -1;return res;}// 11011100 -> 11100000 -> 11100 -> 111 -> 11 -> 11100000 | 11 = 11100011int calMax(int x){// 加上最低位1,01->10,并清空末尾连续1int pre = x + (x & (-x));// 取反相与,得到末尾连续1int suff = x & (~pre);// 去掉末尾0,右移或者除以2,除以最低位1个的位数的2suff /= (x & (-x));// 由于末尾连续1中最高位1在01->10中被用到,所以除去一个1suff >>= 1;return pre | suff;}
}
41、位运算计算乘法
- 表示成B个A相加就很简单,但这样没用位运算
- 如果要用位运算解题,
A*B = (A/2)*(B*2) = (A>>1)*(B<<1) - 如果A是偶数,上式成立,如果A是奇数,需要加一个B
class Solution {public int multiply(int A, int B) {// 表示成B个A相加就很简单,但这样没用位运算// 如果要用位运算解题,A*B = (A/2)*(B*2) = (A>>1)*(B<<1)// 如果A是偶数,上式成立,如果A是奇数,需要加一个Bif (A==0 || B==0) return 0;if (A==1) return B;if ((A&1)==0){return multiply(A>>1, B<<1);}else{return multiply(A>>1, B<<1)+B;}}
}
42、有重复元素的全排列怎么写?

- 每次从后面选一个交换位置,用set去重
- 如果不能用set,就要排序,每次从相同的字符中只选一个加入res
class Solution {List<String> res;char[] ch;public String[] permutation(String s) {// 每次从后面选一个交换位置,用set去重// 如果不能用set,就要排序,每次从相同的字符中只选一个加入resthis.ch = s.toCharArray();Arrays.sort(ch);res = new ArrayList();dfs(new StringBuilder());return res.toArray(new String[res.size()]);}void dfs(StringBuilder sb){if (sb.length()==ch.length){res.add(sb.toString());return ;}for (int i=0;i<ch.length;i++){// 为空,或者前面相同字符只选第一个if (ch[i]=='#' || (i>0 && ch[i]==ch[i-1])) continue;char temp = ch[i];sb.append(ch[i]);ch[i] = '#';dfs(sb);// 还原sb.deleteCharAt(sb.length()-1);ch[i] = temp;}}
}













)

)


)
