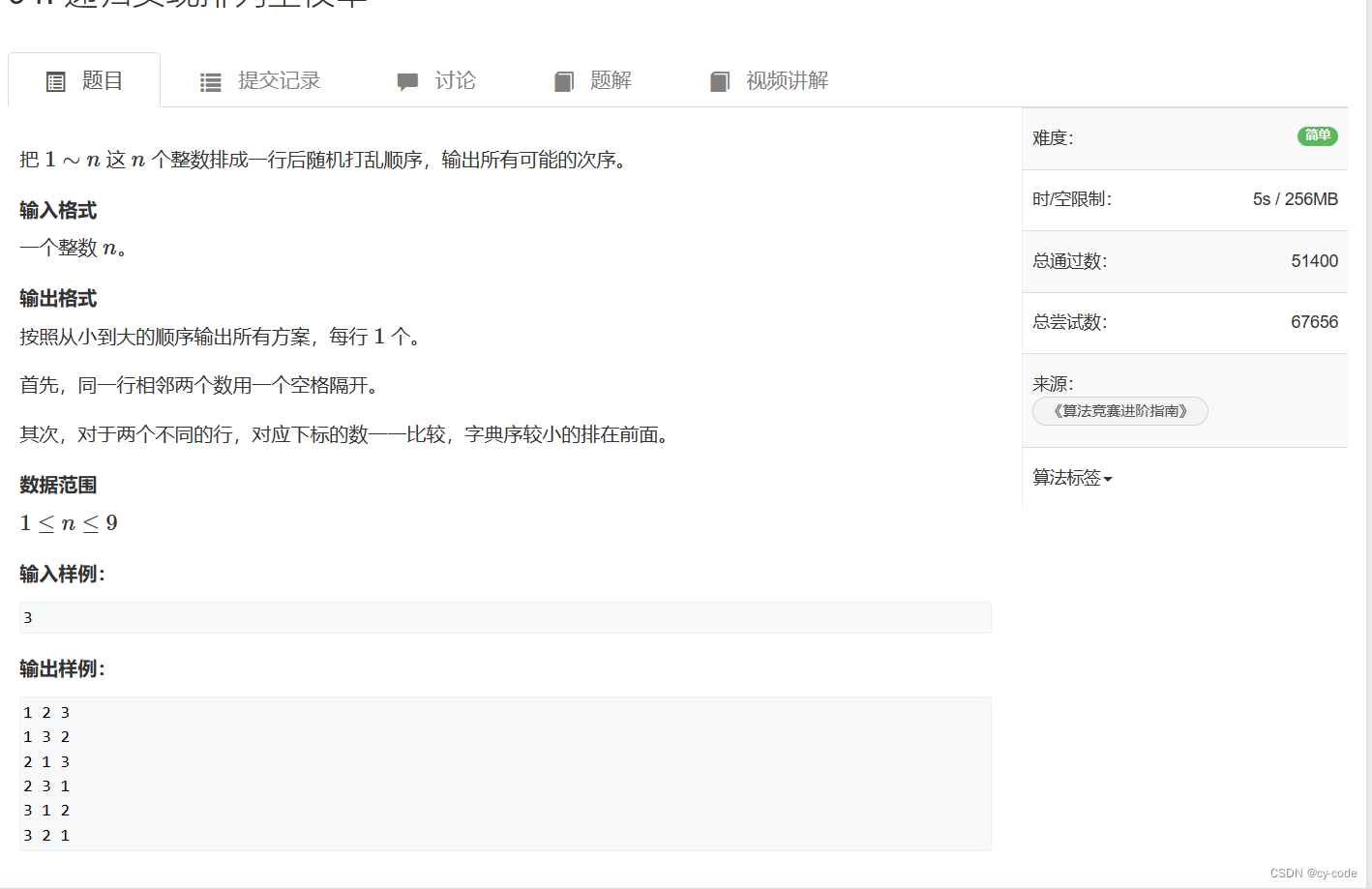
递归实现排列
留着明早省赛之前看
#include<iostream>
using namespace std;
int arr[10010];
int brr[10010];
int n,k;
void dfs(int num){if(num > n){for(int i = 1;i <= n;i++){cout << arr[i] << " ";}cout << endl;return;}for(int i = 1;i <= n;i++){if(brr[i] == 0){brr[i] = 1;arr[num] = i;dfs(num + 1);brr[i] = 0;arr[num]= 0;}}
}
int main()
{cin >> n >> k;dfs(1);return 0;
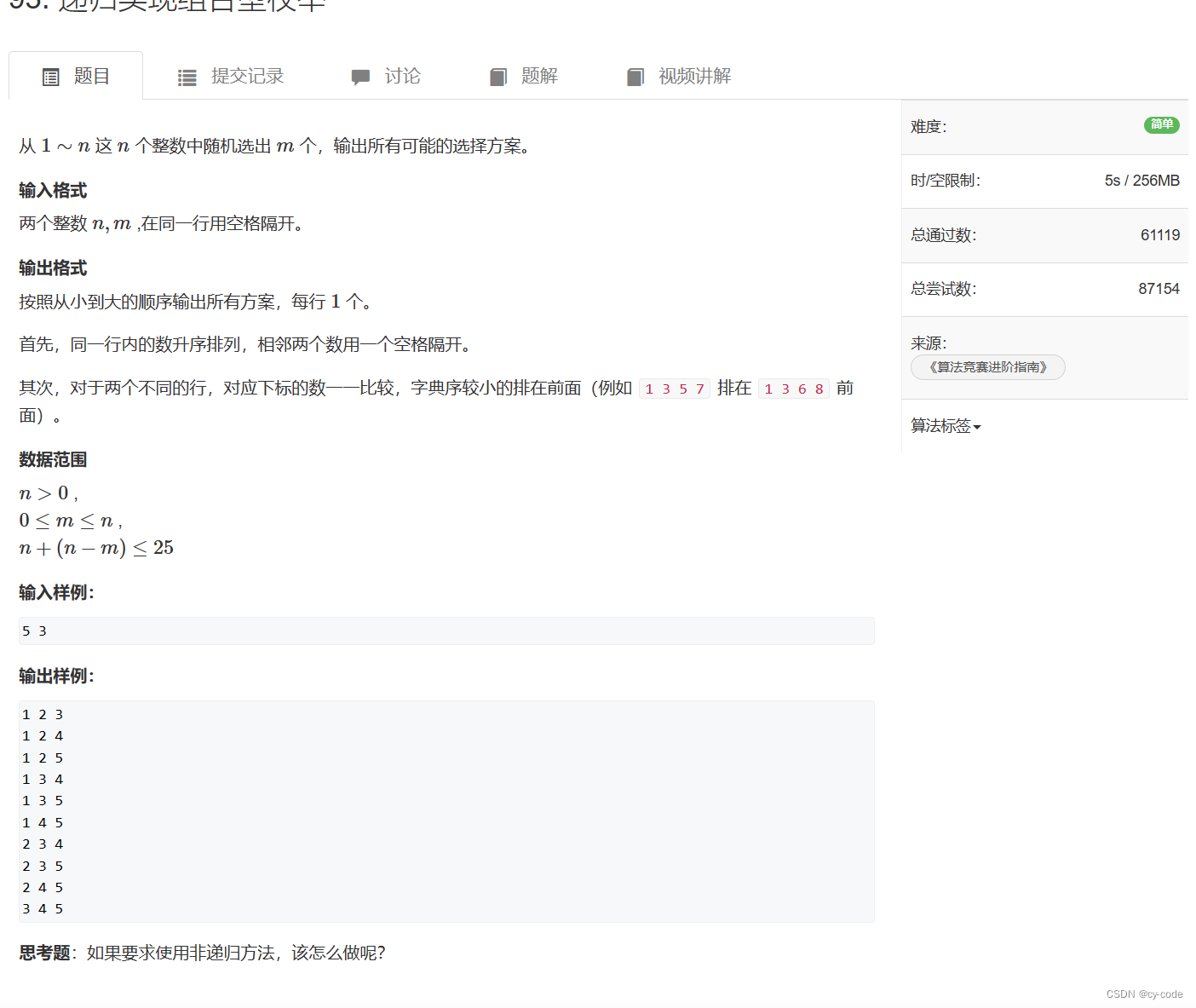
}递归实现组合型枚举
#include<iostream>
using namespace std;
int arr[10010];
int brr[10010];
int n, k;
void dfs(int num,int start) {if(num - 1 + n - start + 1 < k){return;}if (num > k) {for (int i = 1; i <= k; i++) {cout << arr[i] << " ";}cout << endl;return;}for (int i = start; i <= n; i++) {arr[num] = i;dfs(num + 1, i + 1);arr[num] = 0;}
}
int main()
{cin >> n >> k;dfs(1,1);return 0;
}递归实现指数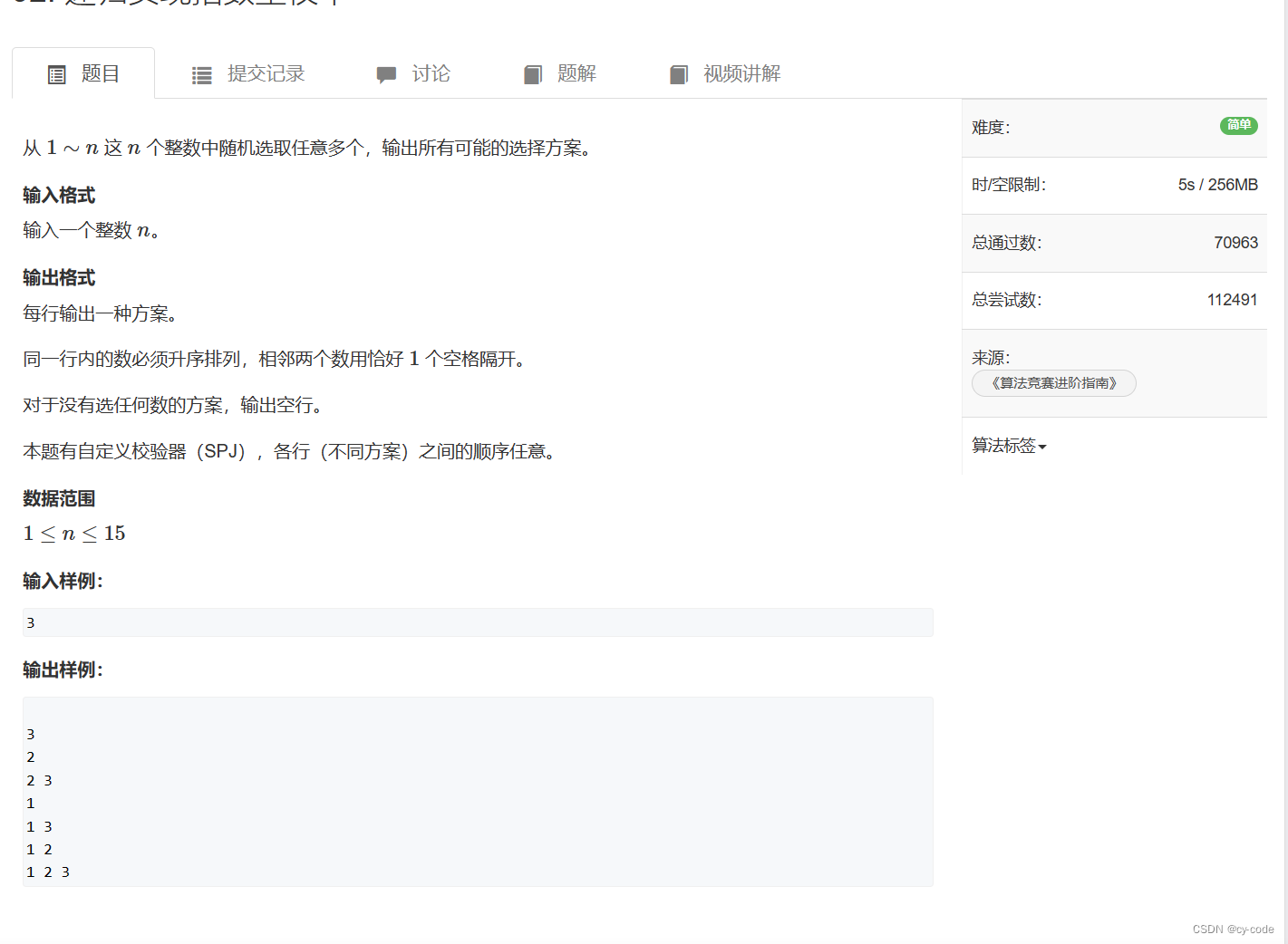
#include<iostream>
using namespace std;
int n;
int* arr = new int[10000] {0};
int main()
{void dfs(int);cin >> n;dfs(1);
}
void dfs(int x) {if (x > n) {for (int i = 1; i <= n; i++) {if (arr[i] == 1) {cout << i << " ";}}cout << endl;return;}arr[x] = 2;dfs(x + 1);arr[x] = 0;arr[x] = 1;dfs(x + 1);arr[x] = 0;
}







英伟达成为最伟大AI企业的核心奥义)





方式)
_DFS)
)


