该论文引入Transformer,主要核心是自注意力机制,自注意力(Self-Attention)机制是一种可以考虑输入序列中所有位置信息的机制。
RNN介绍
引入RNN为了更好的处理序列信息,比如我 吃 苹果,前后的输入之间是有联系的。
如图:
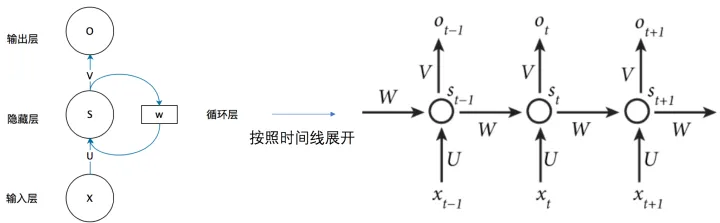
引入Transformer的原因
- 解决长距离依赖的问题:传统的RNN存在梯度消失和梯度爆炸的问题,难以有效捕获长距离依赖关系。而Transformer引入了注意力机制,使模型可以在序列中捕获远距离依赖关系。
- 并行计算:RNN和循环连接的特点使得它们难以并行计算,限制了计算速度。相比之下,Transformer模型的注意力机制允许模型在每个时间步骤上并行计算,大大加速计算速度。
- 可扩展性:Transformer模型可以适用与不同长度的序列
Attention函数分析
注意力机函数值注意力机制的核心组成部分,它定义了如何计算注意力权重,以及使用这些权重聚合数据来获取上下文表示。注意力函数包括:
- Query:查询用于确定关注哪些输入元素的向量或表示。在自注意力机制中,通常是前一个时间步骤的隐藏状态或者上下文表示。
- key:键是与输入元素相关的向量表示。注意力机制通过比较query和key的相似性来决定要关注哪些输入
- value:值是与键对应的输入元素的向量或表示。注意力机制根据query和key的相似性来为每个值分配权重,这些权重将用于生成上下文表示。
- score:分数表示key和query的相似性,分数越高表示查询更关注与键相关的输入。例如向量a和向量b,它的点积
,
越小,
越大,两个向量之间 相似性越高。
- 注意力权重:是一个概率分布,表示对每个输入元素的关注程度。通常由softmax得到,确保总和为1.
- 上下文表示:通过注意力权重对值进行加权求和得到,它是对输入元素的聚合表示,反应了模型的关注点。
注意力函数的一般计算步骤
- 计算query和key的相似性分数,通过点积、加性模型或者缩放点积等方式实现。
- 对相似性分数进行softmax操作,以此获得注意力权重,确保他们归一化为概率分布。
- 使用注意力权重对值加权求和,以此生成上下文表示。
对于自注意力机制来说
- query、key、value:自注意力的核心是通过三个线性变换来为每个位置生成这三个向量。这些向量在输入序列中的每个位置都有一个。对于给定的位置,query 用于提出问题,key 用于提供答案的位置信息,而value 包含了实际的信息。
- 计算注意力分数:计算分数通过将query和所有位置的key 进行点积操作得到的。注意力分户可以看成是度量两个位置之间关联性的分数,他表示了一个位置对于其他位置的关注程度。
- softmax 操作进行归一化:为了获得有效的注意力权重,对计算得到的注意力分数进行归一化处理。为了确保每个位置权重是有效的概率分布,从而更好的表达位置之间的关联性。
- 计算加权和:对得到的归一化之后的注意力权重和对应位置的value进行加权求和,得到每个位置的上下文表示。
多头注意力机制
是一种扩展的自注意力机制,它允许模型同时学习多个不同的关注模式。多头注意力机制将自注意力计算分为多个头,每个头学习不同的权重矩阵,以捕获不同类型的关联性。多个头的结果会拼接或合并,然后通过线性变换进行投影。
选择缩放点积原因
- 点积和加性注意力理论复杂度相似,但是在实践中点积注意力的速度更快、更节省空间,因为它可以使用高度优化的矩阵乘法代码来实现
- 对于键K的维度
越大,加性注意力的性能比点击好,所以我们怀疑对于很大的维度,点积会大幅度增长,为了抵消这种影响,我们使用缩小点积。
缩放点积
是注意力机制中一种常见的类型,通过和自注意力机制一起使用,它的目的是确保在计算注意力分数的时候,使得范围适中,避免梯度消失或者梯度爆炸。下面是介绍缩放点积的步骤:
- Query、Key、Value:这是缩放点积的三个输入,通常来自于一个序列。
- 相似性分数计算:计算查询和键之间的相似性。将查询和键之间的点积作为相似性分数。具体而言就是,对于给定的查询Q和键K,计算相似性分数矩阵为:
其中K^T表示键K的转置矩阵。每个Scores[i][j]表示查询的第i个元素和键的第j个元素的相似性。Score = Q*K^T - 缩放:为了稳定训练过程,缩放点积对相似性分数进行缩放操作,通过操作是除以一个缩放因子来实现。缩放因子通常是键K的维度
的平方根。即:
.缩放后的相似性分数Scale_Scores有助于控制梯度大小,防止梯度爆炸或者消失。
Scale_Scores = Scores / sqrt(d_k) - 计算注意力权重:对缩放后的相似性分数进行softmax操作,将其转化为概率分布,得到注意力权重。这些权重表示了对输入序列不同位置的关注程度。
attention_weight = softmax(Scale_Scores)
结论
在这项工作中,提出了 Transformer,这是一个完全基于注意力的序列转换模型。注意,用多头自注意力取代了编码器-解码器架构中最常用的递归层。





)


Nacos配置中心参数自动刷新测试)
-4-XP行泊一体方案功能规范)


的基本概念——C语言)


函数学习)



