💞💞 前言
hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:viperrrrrrr的博客
💥 欢迎学习数学建模算法、大数据、前端等知识,让我们一起向目标进发!
基于近红外光谱的肠溶片最优包衣厚度终点判别法
包衣是将片剂的外表面均匀地包裹上一层衣膜的过程,旨在控制药物在胃肠道中的释放部位和速度,遮盖苦味或不良气味,防潮、避光,改善外观等。然而,包衣膜太薄或太厚都不利于药效,并且包衣终点的判断方法目前存在一定的难度。近红外光谱技术(NIRS)是一种高效、无需试剂、无污染的分析方法,通过近红外光谱仪、化学计量学软件和应用模型,能快速、简便地实现多组分检测。为实现包衣终点的准确判断,对数据进行分析并完成以下问题:
问题一:对药品在不同包衣时间段包衣片剂的近红外光谱进行特征峰提取,选择具有有效信息的波长片段,即波长选择。
问题二:分析药品包衣厚度分类规律,建立合适的模型对药品包衣不同厚度进行划分,给出方法及结果,并进行灵敏度分析。
问题三:对于不同的包衣厚度,通过建立模型分析包衣之间的关联性,判别出最优的包衣厚度。
我们本次主要解决问题三。
问题三
依据问题一选取的特征峰数据以及问题二的初始分类建立判别模型进行包衣终点判别,最终达到该判别模型能够根据样本不同包衣时间段在各谱区吸收值准确预测该样本是否为最优包衣厚度。
1、Bayes判别
针对问题三,本文使用问题一提取的特征峰数据和问题二聚类得到的初始分类作为判别模型的自变量和分组标记。通过Bayes判别对数据在分类,通过对比判别前后的差异反馈判别的正确率。当正确率较大时,说明该判别方法准确有效,能过对未知分组样本做准确的判别即是否为最优包衣厚度判别,达到有效预测的目的。除此之外,本文还通过梯度分析算法,采用Goldstein原则确定最优步长,同时利用Wolfe法线性搜索,确定损失函数,即我们想要优化的目标。 最后通过迭代,不断刷新损失函数的梯度和参数,迭代次数越多,越接近目标值。
对于解决不确定统计分析的问题,每个类别的样本取得不同特征向量的概率,实现依据某个待识别向量计算该样本每个类别的概率。对应关系公式4所示:
表3 部分符号说明
| 贝叶斯分类 | 贝叶斯公式 |
| 每类样本的整体出现概率 | 先验概率  |
| 每个类中样本取得某个具体特征向量的概率 | 类条件概率 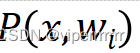 |
| 要计算的样本取得某一个具体特征向量时属于每一类的概率 | 后验概率  |
计算公式如下:
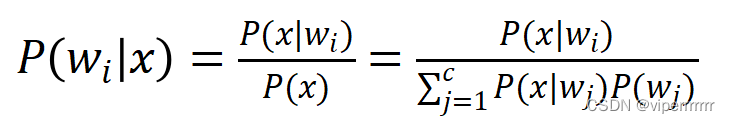
(4)
以问题二的聚类结果为基础数据,对问题一所提取的特征峰数据标记初始分组,通过Bayes准则下的判别分析方法,对数据进行判别再次划分类别,通过比对Bayes判别前后样本所属类别与初始分组是否一致,计算判别的准确性[4]。针对问题三,我们选取问题一提取的特征峰数据,对不同的包衣时间段各谱区的吸收值,最优包衣在谱区的吸收值和素片在谱区的吸收值进行Bayes判别。初始组别是根据问题二的聚类结果分组。其中组别1表示包衣不足,组别3为最优包衣组,组别三表示除组别1和组别2外的其他包衣样本的集合。如下表所示,1组中有一个样本被重新分组到了第3组,第2组和第3组分组完全正确。最终该Bayes判别预测模型的正确率高达99.3%。而且我们特别关注的第3组(最优包衣)不存在误判,说明该模型判别效果较佳,能够作为预测模型对未知分组样本做准确的最优包衣终点判别。
| 表4 分类结果a | ||||||
| 案例的类别号 | 预测组成员 | 合计 | ||||
| 1 | 2 | 3 | ||||
| 初始 | 计数 | 1 | 51 | 0 | 1 | 52 |
| 2 | 0 | 51 | 0 | 51 | ||
| 3 | 0 | 0 | 47 | 47 | ||
| % | 1 | 98.1 | .0 | 1.9 | 100.0 | |
| 2 | .0 | 100.0 | .0 | 100.0 | ||
| 3 | .0 | .0 | 100.0 | 100.0 | ||
| ||||||
2、梯度分析算法
在梯度下降算法中,采用Goldstein原则确定最优步长,同时利用Wolfe法线性搜索,确定损失函数(objective function),来代表了我们想要优化的目标。起初,我们需要初始化部分参数,然后开始迭代过程。在每一次迭代中,都会计算出当前参数下损失函数的梯度,并利用该梯度来更新我们的初始参数。因为该方法下迭代次数越多,越接近目标值即包衣终点。
由于样本对不同包衣时间段在各谱区的吸收值存在在线性关系,故建立线性模型如下:
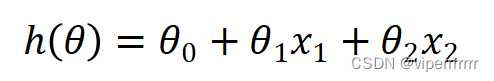
(5)
假设其损失函数为:
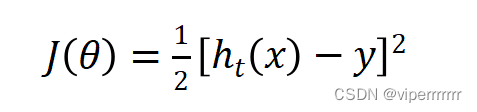
(6)
下一步对损失函数最小化,即对
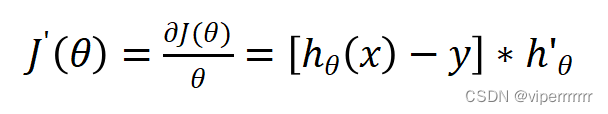
求导:
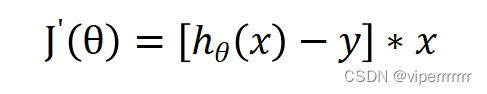
(7)
其中
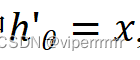
,所以不难得出:

(8)
结果如下图所示,其中图中黑色曲线表示梯度下降算法下降时的轨迹。

图7 梯度下降算法结果
样本数据通过迭代过程,最终收敛求得反馈数据即为包衣终点判别结果。
5.3.3灵敏度分析
敏感性分析(sensitivity analysis)是指从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。每个输入的灵敏度用某个数值表示即敏感性指数(sensitivity index)。SALib是一个基于python进行敏感性分析并提供一个解耦的工作流的开源库,负责使用其中一个采样函数(sample functions)生成模型输入,并使用其中一个分析函数(analyze functions)计算模型输出的灵敏度指数。本文使用蒙特卡洛技术实现全局灵敏度分析,基于方差的方法(sabol方法)将输入和输出的不确定性量化为概率分布,并将输出方差分解为可归因于输入变量和和变量组合的部分。因此,通过该输入引起的输出变化量来度量输出对输入变量的敏感度。本文根据不同包衣时间的肠溶片对成分1和成分2波长下的吸收波变化率和包衣时间进行拟合和灵敏度分析,结果如下:
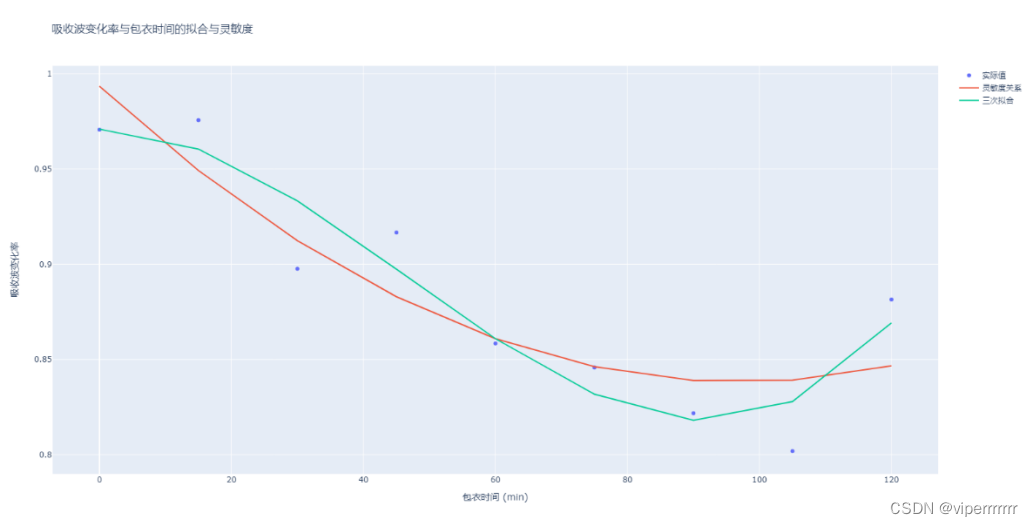
图8 成分1的灵敏度分析
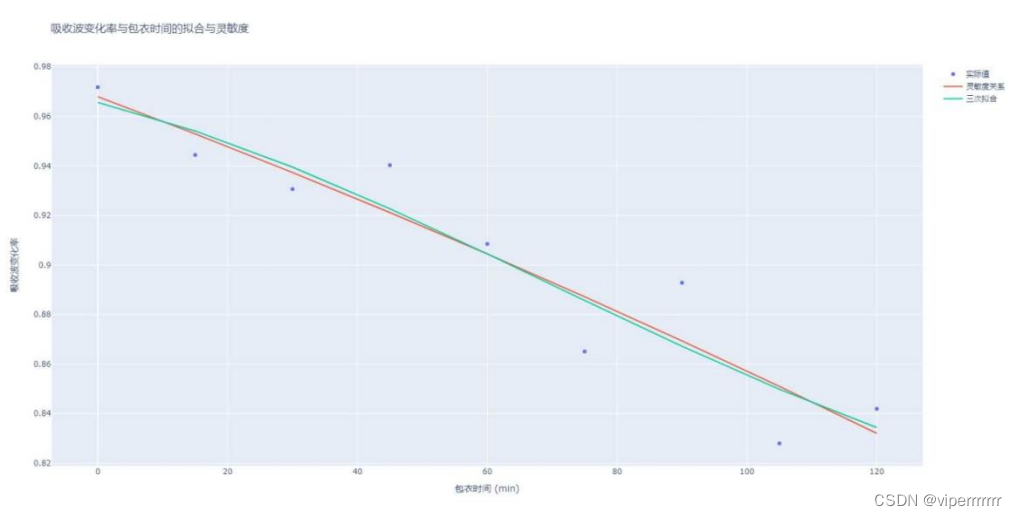
图9 成分2的灵敏度分析
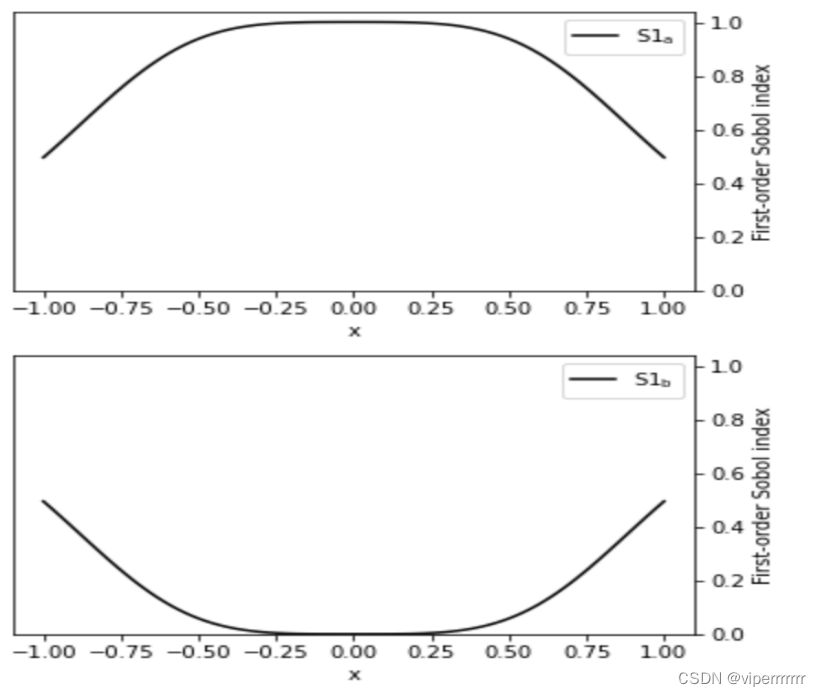
图10 灵敏度拟合图
由图可知,在经过二次拟合再三次拟合之后不同包衣时间下的肠溶片对波长的吸收值二阶灵敏度和总灵敏度。(一个二阶灵敏度会涉及两个变量), 而对应他们名字加上_conf 则表示对应的置信度(95%)。从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。每个输入的灵敏度用某个数值表示即敏感性指数(sensitivity index)每个x对应不同a,b取值下y的均值以及95%置信区间,得到右图为参数a,b的一阶指数。由图可知,再保证其拟合度不变的情况下,随着时间增加其灵敏度越高,但再一定程度之后其灵敏度将会下降。
--- 使用对象)
)


)



(2))


)





Lammps中的Walls墙)

