整数划分（计数类dp）-java

整数划分我们主要通过两种思路来对这道题就行解决。

文章目录

前言

一、整数划分

二、模拟完全背包

三.代码如下

1.代码如下

2.测试样例

3.代码运行结果

四、计数类dp

4.1算法思路

4.2代码如下

总结

前言

整数划分我们主要通过两种思路来对这道题就行解决。

提示：以下是本篇文章正文内容，下面案例可供参考

一、整数划分

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中 n1≥n2≥…≥nk,k≥1。

我们将这样的一种表示称为正整数 n 的一种划分。

现在给定一个正整数 n，请你求出 n共有多少种不同的划分方法。

二、模拟完全背包

我们可以把1到n看成背包的容积，然后n1、n2.....nk看成物品，这个问题就转化成不限物品的次数，且恰好能装满背包容量的问题

我们引入二维数组dp，dp[i][j]表示的含义是用前i个数构成整数j所需要的方案数。

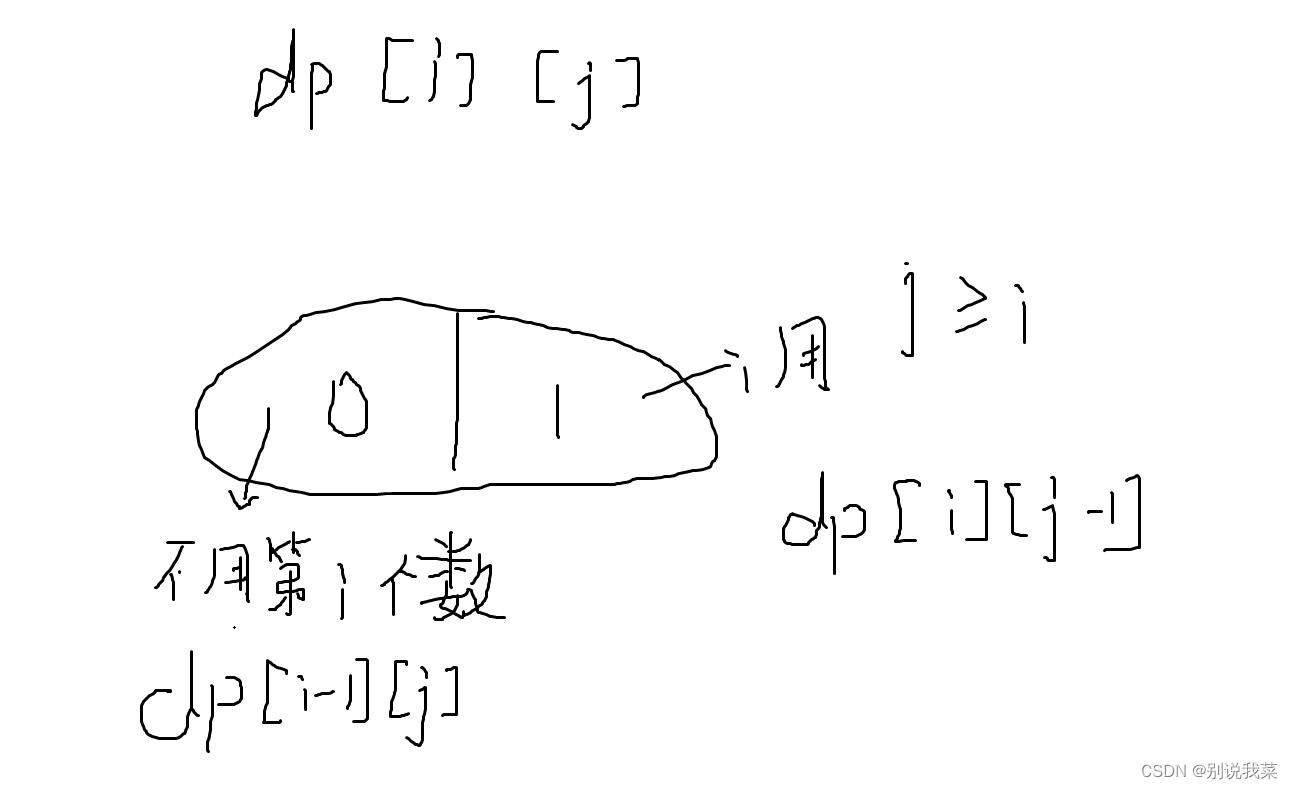
图1.1思路模拟

第i个数不用时：

dp[i][j] = dp[i-1][j]

当我们用第i个数时：

$dp[i][j] = dp[i-1][j] + dp[i][j-i]$

$dp[i][j-i] = dp[i-1][j-1*i]+dp[i-1][j-2*i]+dp[j-3*i]......$

这一步跟完全背包类似，不同的是我们需要求所有的方案之和。

当然我们还需要考虑一些边界情况比如当j为0的时候，我们本身就有一种由0构成的方案

$dp[i][0] = 1$

$n\geqslant i\geqslant 0$

三.代码如下

1.代码如下

package AcWing;import java.io.*;
import java.util.*;public class 整数划分 {static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int M =(int) 1e9+7;public static void main(String[] args) {Scanner sc = new Scanner(br);int n = sc.nextInt();int[][] dp = new int[1010][1010];for(int i = 0;i <= n;i++){//相当于总和为0，那么我们可以由0构成，也是一种方案dp[i][0] = 1;}//相当于哪个物品for(int i = 1;i <= n;i++){for(int j = 1; j <= n;j++){dp[i][j] = dp[i-1][j] % M;if(j >= i){dp[i][j] = (dp[i][j-i]+dp[i-1][j])%M;}}}pw.println(dp[n][n]);pw.flush();}
}

2.测试样例

3.代码运行结果

四、计数类dp

4.1算法思路

我们引入二维数组dp，dp[i][j]表示所有总和为i，恰好为j个数相加的方案数。那么我们就可以枚举

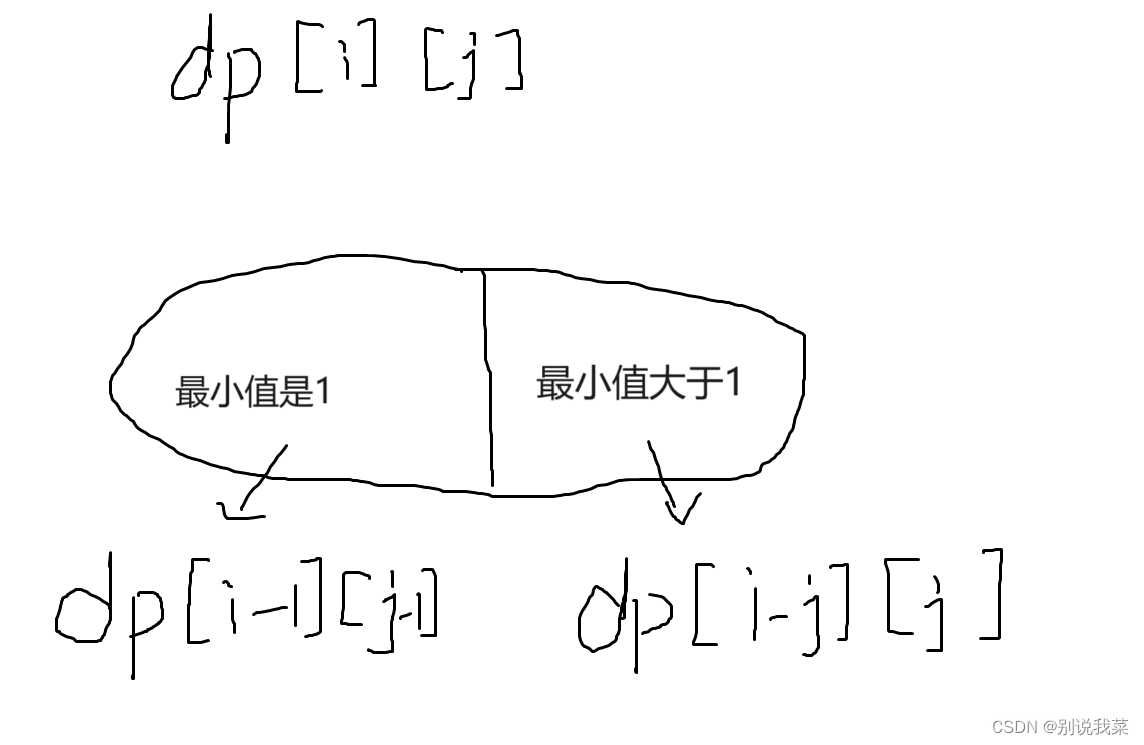
图4.1模拟思路

dp[i][j]的值就可以分成两种情况：

（1）当被拆分的整数里面的最小值是1是，那我们就可以让取dp[i-1][j-1]的值，即我们减去一个已知的最小值1，剩下总和为i-1，恰好由j-1个数构成的方案数。

（2）当被拆分的整数里面的最小值大于i时，那么我们先减去j个1，那么总和为i-j的由j个数构成的方案里面的最小值就一定是大于1的，即dp[i-j][j]

$dp[i][j] = dp[i-1][j-1]+dp[i-j][j]$

那么我们最后输入的结果为：

$result = dp[n][1] + dp[n][2].....+dp[n][n]$

4.2代码如下


import java.io.*;
import java.util.*;public class Main {static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));static int mod = (int)1e9+7;public static void main(String[] args) {Scanner sc = new Scanner(br);int n = sc.nextInt();int[][] dp = new int[1010][1010];dp[0][0] = 1;for(int i = 1; i<= n;i++){//总和为i，那么最多就有i个数相加for(int j = 1;j <= i;j++){dp[i][j] = (dp[i-1][j-1] + dp[i-j][j])%mod;}}int res = 0;for(int i = 1; i<= n;i++){//这里注意也要对mod取余，防止结果爆intres =(res + dp[n][i]) % mod;}pw.println(res);pw.flush();}}