Fix a Tree

传送门

A tree is an undirected connected graph without cycles.

Let’s consider a rooted undirected tree with $n$ vertices, numbered $1$ through $n$ . There are many ways to represent such a tree. One way is to create an array with $n$ integers $p_1,p_2,...,p_n$ , where $p_i$ denotes a parent of vertex $i$ (here, for convenience a root is considered its own parent).

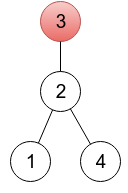
For this rooted tree the array $p$ is $[2,3,3,2]$ .Given a sequence $p_1,p_2,...,p_n$ , one is able to restore a tree:

1. There must be exactly one index $r$ that $p_r=r$ . A vertex $r$ is a root of the tree.
2. For all other $n-1$ vertices $i$ , there is an edge between vertex $i$ and vertex $p_i$ .

A sequence $p_1,p_2,...,p_n$ is called valid if the described procedure generates some (any) rooted tree. For example, for $n=3$ sequences (1,2,2), (2,3,1) and (2,1,3) are not valid.

You are given a sequence $a_1,a_2,...,a_n$ , not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

Input

The first line of the input contains an integer $n$ ( $2<=n<=200000$ ) — the number of vertices in the tree.

The second line contains $n$ integers $a_1,a_2,...,a_n$ ( $1<=a_i<=n$ ).

Output

In the first line print the minimum number of elements to change, in order to get a valid sequence.

In the second line, print any valid sequence possible to get from $(a_1,a_2,...,a_n)$ in the minimum number of changes. If there are many such sequences, any of them will be accepted.

Examples

input #1

4
2 3 3 4

output #1

1
2 3 4 4

input #2

5
3 2 2 5 3

output #2

0
3 2 2 5 3

input #3

8
2 3 5 4 1 6 6 7

output #3

2
2 3 7 8 1 6 6 7

Note

In the first sample, it’s enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex $4$ (because $p_4=4$ ), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex $3$ (right drawing below). On both drawings, roots are painted red.

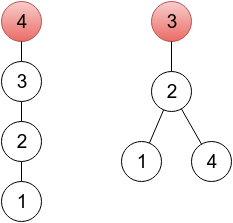
In the second sample, the given sequence is already valid.

题面翻译

对于下图中的树，

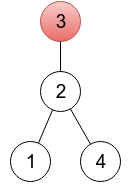
可以用数组表示为 $[2,3,3,2]$。这种可以表示树的数组（即有效）需要符合以下条件：

1. 有且只有一个索引 $r$ ，符合 $p_r=r$ 。其中顶点 $r$ 是树的根。
2. 对于所有剩下的 $n-1$ 个顶点 $i$ 一定要有在 $i$ 和 $p_i$ 之间的边。

比如 数列 $(1,2,2)$、$(2,3,1)$ 和 $(2,1,3)$ 都是因为根的数目而导致不有效。

现在给你一个数组 $a_1,a_2,\cdots ,a_n$，不一定是有效的。你需要对数组里面的值，通过最小次数的更改，使得这个数组有效。

并输出最小更改次数和一个通过最小更改次数而更改成功的有效数组。

如果有多种解，只需说出任何一组。

输入格式

第一行是一个整数 $n(2\le n\le 200000)$ ----树的顶点个数。

第二行包含 $n$ 个整数 $a_1,a_2,\cdots ,a_n(1\le a_i\le n$。

输出格式

第一行一个整数，最小更改次数。

第二行输出任意一个通过最小更改次数而更改成功的有效数组。

说明

• 第一个样例只需要改一个就好啦！第一个样例输出是一个扎根于顶点 $4$ 的树（因为 $p_4=4$），你可以在下面的图中看到。另一个正确的答案应该是数列 $2,3,3,2$，扎根在顶点 $3$，也可以在下面的图中看到。两个图中顶点将用红色标出。

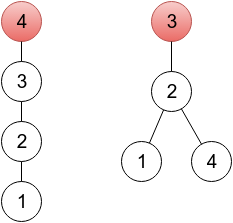
• 第二个样例中，给出的数列已经是有效的了。

注明

$以上来自CodeForces，翻译来源：洛谷。$

BestMonkey：CodeForces 你什么时候能完善一下你的 Markdown 格式啊！你知道我复制下来题面还要一个一个删多余的空格吗！你看看人家洛谷啊！（愤怒）
CodeForces：我这是为了提高你们的编辑文本效率啊。（叉腰）
BestMonkey：（直接一拳）

解题思路

先考虑确定根节点：

• 显然，最后只有根节点是自环。所以，若输入中有自环，那就选它为树的总根。显然，答案不会更劣；
• 如果一开始没有自环，那选择环上一点作为根即可。

然后处理环。用一个数组存下环上节点的颜色。对于每一个节点染色后 DFS（染的颜色要与之前不同），若找到一个节点颜色与当前节点相同，则说明找到了一个环。此时，只要把当前的点指向总根即可。若没有总根，则设置当前节点为总根，再将当前节点的父亲设为自己。

AC Code

#include<bits/stdc++.h>
using namespace std;
char buf[1048576], *p1, *p2;
template<typename T>inline void Super_Quick_Read(T &x) {bool f = 1;x = 0;char ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);while (ch < '0' || ch > '9') {if (ch == '-') f = !f;ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);}while (ch >= '0' && ch <= '9')x = (x << 1) + (x << 3) + (ch ^ 48), ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);x = (f ? x : -x);return;
}
template<typename T>inline void Quick_Write(T x) {if (x < 0) putchar('-'), x = -x;if (x > 9) Quick_Write(x / 10);putchar(x % 10 + '0');return;
}
int n, a[200005];
int Fa[200005], Color[200005], Root, Tag;
inline void DFS(int u) {if (Color[u]) return;Color[u] = Tag;if (Fa[u] == u) {if (!Root) Root = u;else Fa[u] = Root;return;}if (Color[Fa[u]]) {if (Color[Fa[u]] == Tag) if (!Root) Fa[u] = u, Root = Fa[u];else Fa[u] = Root;return;}DFS(Fa[u]);
}
signed main() {Super_Quick_Read(n);for (register int i = 1; i <= n; ++i) Super_Quick_Read(a[i]);memcpy(Fa, a, sizeof(a));for (register int i = 1; i <= n; ++i) if (Fa[i] == i) {Root = i;break;}for (register int i = 1; i <= n; ++i) ++Tag, DFS(i);int count_change = 0;for (register int i = 1; i <= n; ++i) if (Fa[i] != a[i]) ++count_change;Quick_Write(count_change);puts("");for (register int i = 1; i <= n; i++) Quick_Write(Fa[i]), puts(" ");puts("");return 0;
}