iclr 2024 oral reviewer 评分 688
1 intro
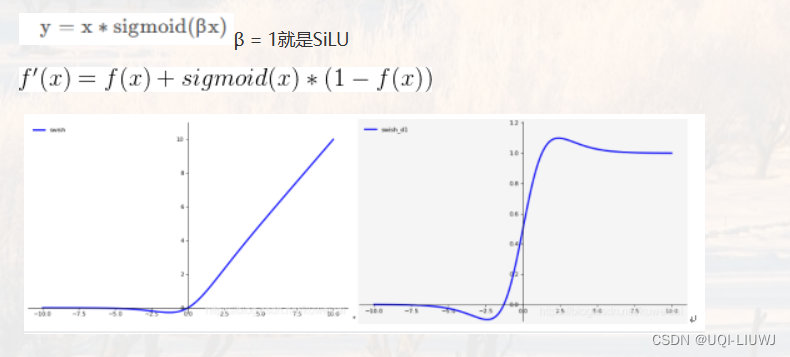
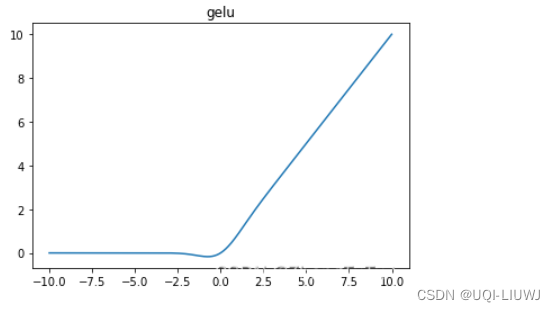
- 目前LLM社区中通常使用GELU和SiLU来作为替代激活函数,它们在某些情况下可以提高LLM的预测准确率
- 但从节省模型计算量的角度考虑,论文认为经典的ReLU函数对模型收敛和性能的影响可以忽略不计,同时可以显着减少计算和权重IO量\
-

-
2 激活函数影响效果吗?
- 选用了开源的大模型 OPT,Llama和Falcon
- 训练数据使用RefinedWeb
- 分别进行了预训练和finetune两个实验
2.1 不同激活函数对比
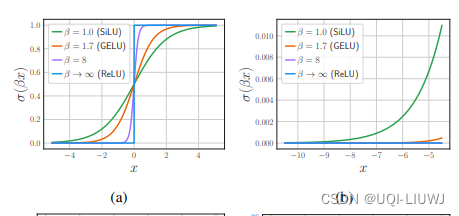
2.2 平均激活稀疏度
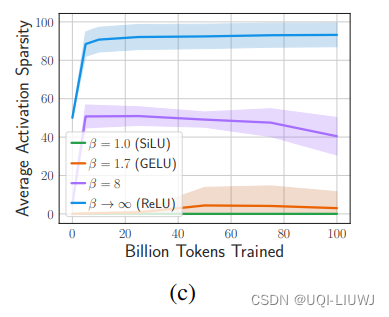
2.3 从头训练,各个激活函数的效果
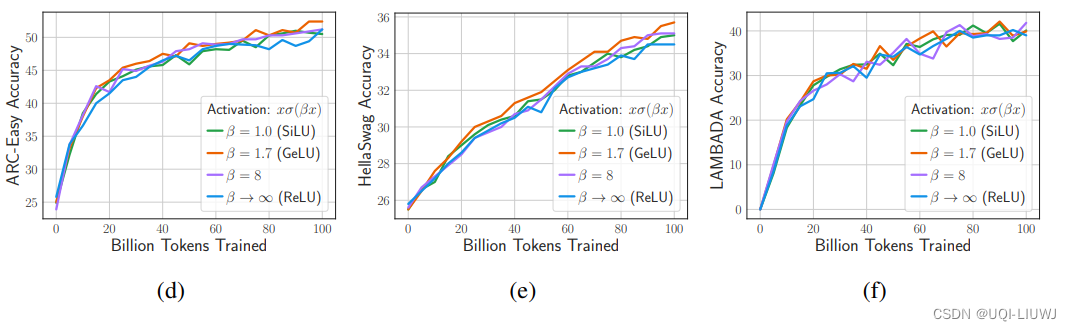
使用不同的激活函数时,模型的性能非常相似。
3 ReLU充当预训练LLM的润滑剂
- 通过上一节的实验,LLM的预测准确率并不依赖于激活函数的类型
- 但现有大多数LLM均使用ReLU之外的激活函数进行训练
- —>为了在推理阶段使这些LLM结合ReLU激活的计算优势,论文进行了各种架构改进实验
- 将ReLU插入到预训练LLM中,模型在微调过程中可能快速的恢复性能,同时提高推理时的稀疏性
- 作者将这一过程称为对LLM的“再润滑”(ReLUfication)
- —>为了在推理阶段使这些LLM结合ReLU激活的计算优势,论文进行了各种架构改进实验
3.1 阶段1:替换非ReLU激活函数成ReLU
- 阶段1:使用ReLU替换到LLM中的其他激活函数
- 在Falcon 和 Llama分别替换 GELU 和 SiLU
- 由于 OPT 模型已经使用 ReLU 激活,因此这里保持不变
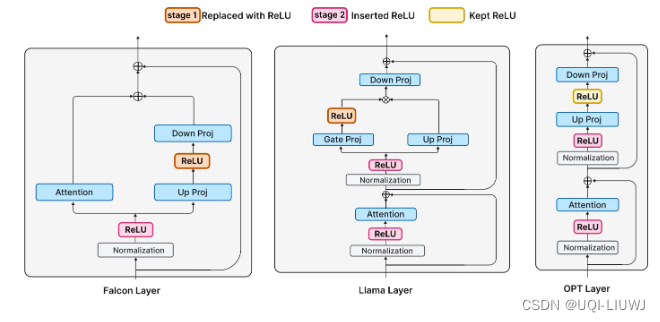
3.1.1 替换后的激活稀疏程度
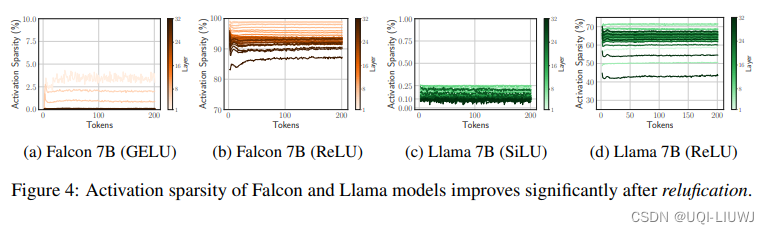
3.1.2 替换后的网络预测倾向
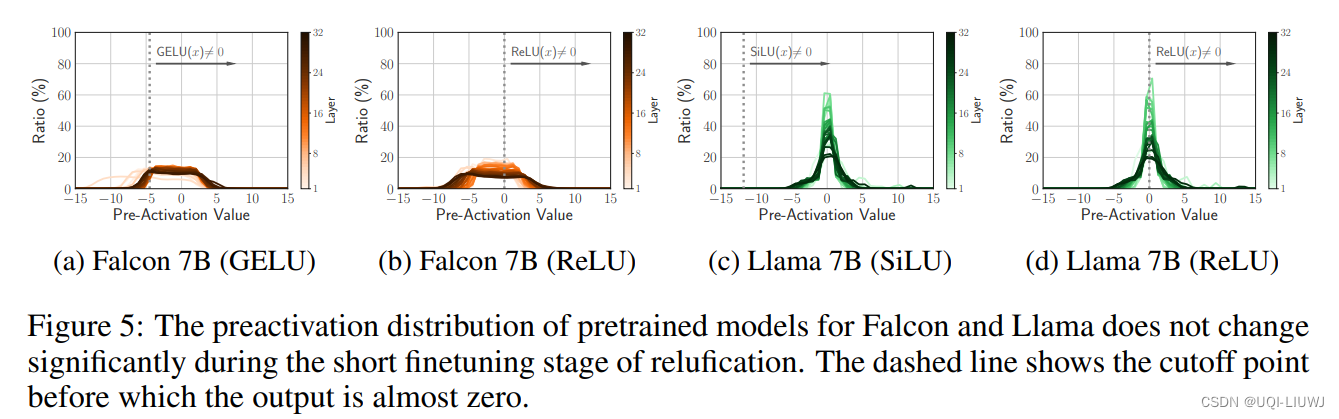
- 论文测量了Falcon 和 Llama 预训练模型的预激活分布情况
- 可以看出,在微调阶段,这个分布本身的变化并不明显
- ——>表明网络的预测倾向在引入稀疏性时并不会改变,具有良好的稳定性
3.1.4 模型预测准确率随ReLU不断微调的变化情况
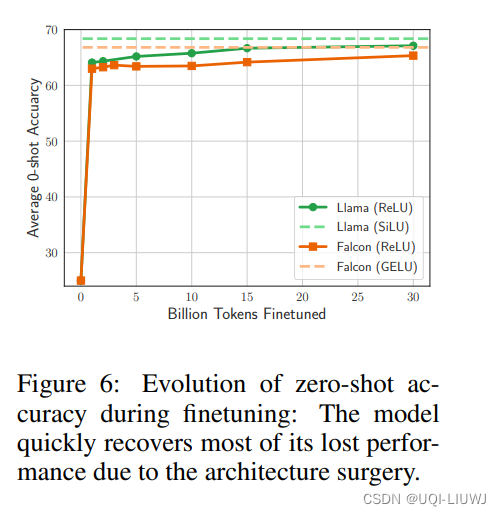
模型在微调阶段很快恢复了其原本的性能,其中Llama(绿色线条)完美的达到了ReLU插入之前的预测准确率
3.2阶段2:进一步稀疏化

- 在一阶段中,作者插入了ReLU来替代其他激活函数,这会导致模型down projection层的输入变稀疏
- 除了down projection层之外,transformer的解码器层中还有其他复杂的矩阵向量乘法
- 例如注意力层中的QKV projection,这些矩阵向量乘法大约占总计算量的约 55%
- ——>对这一部分进行二次稀疏也非常重要
- 在现代transformer层中,注意力层和 FFN 层的输入都来自归一化层(LayerNorm)
- 这些层可以被视为 MLP 的一种特定形式,因为它们并不是学习参数,而是学习如何对输入数据进行缩放
- ——>将ReLU接在归一化层之后来进行二阶段的稀疏激活
3.2.1 进一步稀疏化之后,模型的稀疏程度和zero-shot预测精度
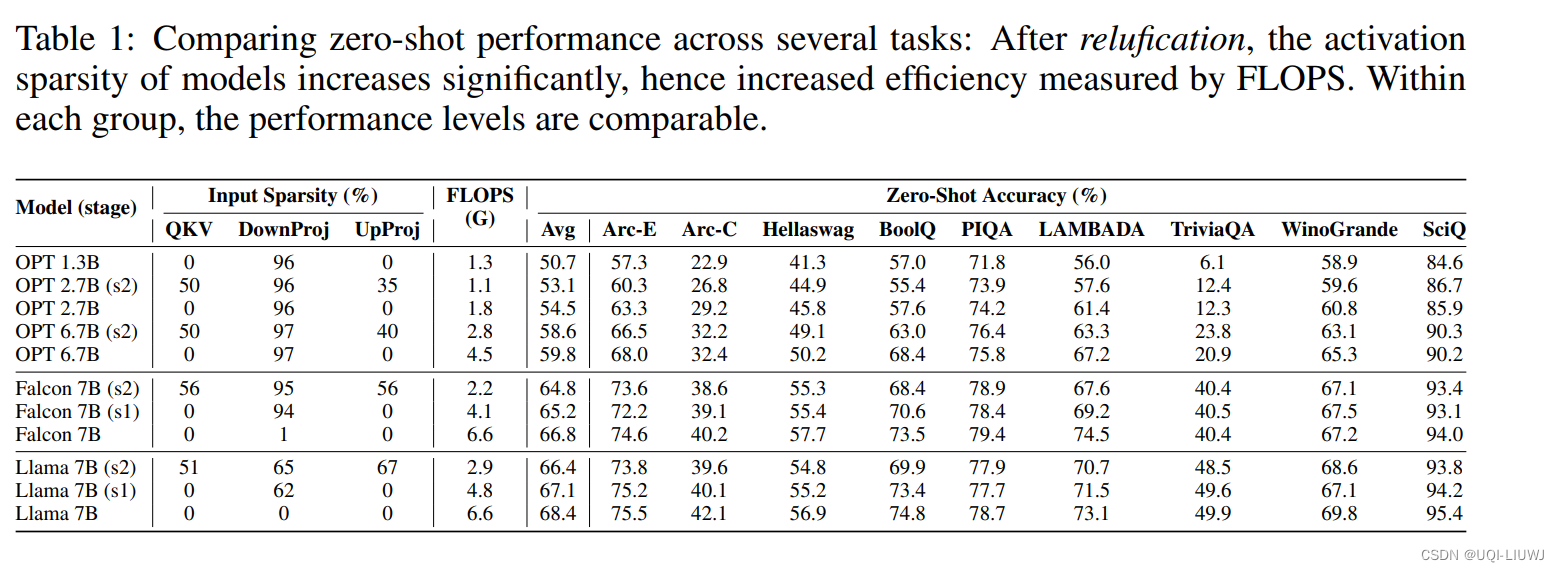
对LLM的不同部位进行稀疏化后,模型的zero-shot精度变化并不明显,但是计算量的差异很大
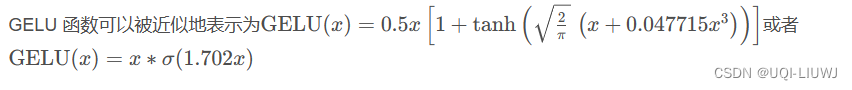






)
--基础知识)


)
)





项目实战)

