卷积神经网络相当于人类的视觉,但是它并没有记忆能力,所以它只能处理一种特定的视觉任务,没办法根据以前的记忆来处理新的任务。比如,在一场电影中推断下一个时间点的场景,这个时候仅依赖于现在的场景还不够,还需要依赖于前面发生的情节。这时候,我们就需要一种具有记忆能力的神经网络,循环神经网络就是这样一种神经网络,它期望网络能够记住前面出现的特征,并依据特征推断后面的结果,而且整体的网络结构不断循环,因此被称为循环神经网络。
循环神经网络通过使用带自反馈的神经元,能够处理任意长度的时序数据。简单循环网络是指只有一个隐藏层的神经网络,在一个两层的前馈神经网络中,连接存在相邻的层与层之间,而循环神经网络增加了从隐藏层到隐藏层的反馈连接。如果我们把每个时刻的状态都看作是前馈神经网络的一层的话,循环神经网络可以看成是时间维度上权值共享的神经网络,如下图所示:
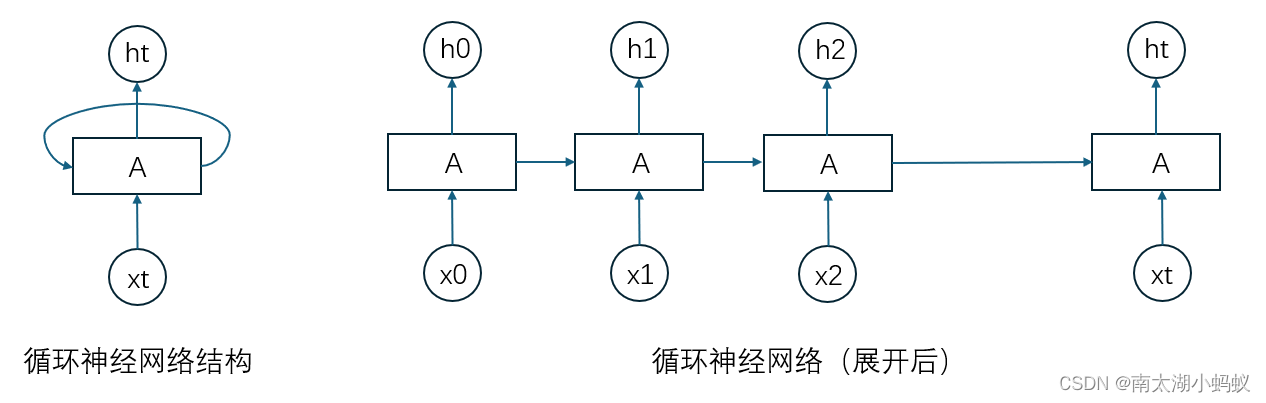
循环神经网络和普通神经网络(多层感知机)最大的差别在于:普通神经网络中,输出是有输入乘以权重加上偏置,再进行非线性运算得到的,也就是y = sigmoid(w*x + b),
而在循环神经网络中,增加了当前节点前面的节点的“记忆”,也就是增加了前面节点的输出乘以权重的值,写成公式就是y = sigmoid(w*x + wh*h + b),其中w是输入x的权重矩阵,wh是隐状态的权重矩阵。
循环神经网络的反向传播算法一般称为“随时间反向传播”算法,该算法的主要思想是通过类似前向神经网络的错误反向传播算法来计算梯度。该算法将循环神经网络看作是一个展开的多层前馈网络,就像上面那个图展开后的样子,其中“每一层”对应循环神经网络中的“每个时刻”,这样,循环神经网络就可以按照前馈网络中的反向传播算法计算梯度。在“展开”的循环神经网络中,所有层的参数是共享的,因此参数的真实梯度是所有“展开层”的参数梯度之和。
循环神经网络可以应用到很多不同类型的机器学习任务。根据这些任务的特点可以分为以下几种模式:序列到类别模式、同步的序列到序列模式、异步的序列到序列模式。
1. 序列到类别模式
基本就相当于输入一个序列数据,输出这个序列数据的类别。典型的就是输入一段话,输出这句话的情感的积极的还是消极的。
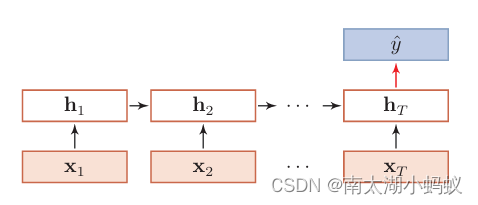
2. 同步的序列到序列模式
每一时刻都有输入和输出,且输入和输出长度相同,比如词性标注,每一个单词都需要标注其对应的词性标签。再比如说,DNA序列分析,输入是一段DNA序列,输出也是一段一一对应的DNA序列。

3. 异步的序列到序列模式
异步的序列到序列模式也被称为编码器-解码器模型,输入和输出不需要有严格的对应关系,也不需要保持相同的长度。典型的就是机器翻译,中文翻译成英文,不需要每个单词都一一对应,但是意思是相同的,这就需要先对中文进行解码,然后再对解码结果编码成英文。

下面我们看一个简单的例子,这个例子是从《动手学深度学习》一书中选取的,不过我改用了循环神经网络实现了一下。
我们先用正弦函数来生成一个有1000个数据的序列:
# 画出sin函数作为序列函数
y = []
for i in range(1000):y.append(np.sin(0.01*i)+np.random.normal(0,0.2)) # 给sin函数增加一个微小的扰动
x = [i for i in range(1000)]plt.plot(x, y)
plt.show()
下面,我们希望用这个序列中的每四个连续的值,去预测下一个值。
total = 1000
tau = 4
features = np.zeros((total-tau, tau))
data = [i for i in range(total)]
for i in range(tau):features[:,i] = y[i:total-tau+i] # 获取到每一列的特征值
print(len(features)) # 样本个数
print(features) # 输出特征值
# 输出 996
[[ 0.16806793 0.14102484 0.01429365 -0.02700145][ 0.14102484 0.01429365 -0.02700145 0.21676487][ 0.01429365 -0.02700145 0.21676487 -0.15535389]...[-0.44295722 -0.4784534 -0.74262601 -0.66540164][-0.4784534 -0.74262601 -0.66540164 -0.40766233][-0.74262601 -0.66540164 -0.40766233 -0.81723738]]可以看到,features是一个996x4的矩阵,我们要做的其实就是用每一行的4个数据去预测下一个值。下面我定义了一个简单的神经网络:
# 构建一个简单的多层感知机来训练
class SimpleNet(nn.Module):def __init__(self) -> None:super().__init__()self.classifier = nn.Sequential(nn.Linear(4, 10), nn.ReLU(), nn.Linear(10, 1))def forward(self, x):x = self.classifier(x)return x下面我将这些数据构造成dataset和dataloader:
# 用前600个数字作为训练集,后400个作为测试集
class myDataset(Dataset):def __init__(self, tau=4, total=600, transform=None):data = [i for i in range(total)]y = []for i in range(total):y.append(np.sin(0.01*i)+np.random.normal(0,0.2)) # 给sin函数增加一个微小的扰动# tau代表用多少个数字来作为输入,默认为4self.features = np.zeros((total-tau, tau)) # 构建了596行4列的输入序列,代表了596个训练样本,每个样本有4个数字构成for i in range(tau):self.features[:,i] = y[i: total-tau+i] # 给特征向量赋值self.data = dataself.transform = transformself.labels = y[tau:]print((self.features))print((self.labels))print(y)def __len__(self):return len(self.labels)def __getitem__(self, idx):return self.features[idx], self.labels[idx]transform = transforms.Compose([transforms.ToTensor()])
trainDataset = myDataset(transform=transform)
train_loader = DataLoader(dataset=trainDataset, batch_size=32, shuffle=False) # 由于序列数据有前后关系,所以不能打乱接下来,对模型进行训练:
def train(epochs=10):net = SimpleNet()net.apply(init_weights)criterion = nn.MSELoss()#criterion = nn.CrossEntropyLoss()optimizer = torch.optim.Adam(net.parameters(), lr=0.001)for epoch in range(epochs):total_loss = 0.0for i, (x, y) in enumerate(train_loader):x = Variable(x)x = x.to(torch.float32)y = Variable(y)y = y.to(torch.float32)optimizer.zero_grad()outputs = net(x)loss = criterion(outputs, y)total_loss += loss.sum() # 因为标签值和输出都是一个张量,所以损失值要求和loss.sum().backward()optimizer.step()print('Epoch {}, Loss: {:.4f}'.format(epoch+1, total_loss/len(trainDataset)))torch.save(net, 'simple.pt')预测并显示预测的结果:
# 预测
net = torch.load('simple.pt')
features = torch.from_numpy(features)
features = features.float()
y_pred = net(features)
# 画出sin函数作为序列函数
y = []
for i in range(996):y.append(np.sin(0.01*i)+np.random.normal(0,0.2)) # 给sin函数增加一个微小的扰动
x = [i for i in range(996)]fig, ax = plt.subplots()
ax.plot(x, y, color="r")
ax.plot(x, y_pred.detach().numpy(), color="g")
plt.show()
可以看到,跟原始数据相比,预测出来的结果也是比较接近的。下面尝试用循环神经网络来实现一下这个简单的功能:
class RNN(nn.Module): def __init__(self, input_size, hidden_size, output_size): super(RNN, self).__init__() self.hidden_size = hidden_size self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) self.fc = nn.Linear(hidden_size, output_size) def forward(self, x): h0 = torch.zeros(1, x.size(0), self.hidden_size).to(x.device)#print("x.shape = ",x.shape)#print("h0.shape = ",h0.shape)out, _ = self.rnn(x, h0)#print("out.shape = ",out.shape)#print("out[:, -1, :].shape = ",out[:, -1, :].shape)out = self.fc(out[:, -1, :])#print("out.shape : ",out.shape)return out注意,这里的out[:,-1,:]代表的是一个三维数组,把第二维最后一个值取出来,看一下代码会比较清晰:
a = [[[1,2,3],[4,5,6],[7,8,9]],[['a','b','c'],['d','e','f'],['h','i','j']]]
t = np.array(a)
print(t[:,-1,:])
# 输出:
[['7' '8' '9']['h' 'i' 'j']]预测结果同样比较准确。
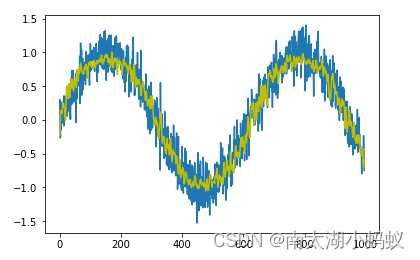
采用循环神经网络其实也可以对图像进行分类,我们以mnist数据集为例,其实只要把mnist数据集看成是28x28的序列数据就行了,一个序列由28个数据组成,每个数据有28个元素构成。
# 超参数
input_size = 28class RNN(nn.Module): def __init__(self, input_size, hidden_size, num_classes): super(RNN, self).__init__() self.hidden_size = hidden_size self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) self.fc = nn.Linear(hidden_size, num_classes) def forward(self, x): h0 = torch.zeros(1, x.size(0), self.hidden_size).to(x.device)out, _ = self.rnn(x, h0)out = self.fc(out[:, -1, :])return out定义一个训练函数
def train(net, data_loader, test_loader, epochs=10):criterion = nn.CrossEntropyLoss()optimizer = optim.Adam(net.parameters(), lr=0.001)for epoch in range(epochs):total_loss = 0.0for i, (images, labels) in enumerate(data_loader):optimizer.zero_grad()# 将图像展平为序列,每个序列的特征数为28images = images.view(-1, 28, input_size)outputs = net(images)loss = criterion(outputs, labels)total_loss += loss.item()loss.backward()optimizer.step()print('Epoch {}, Loss: {:.4f}'.format(epoch+1, total_loss/len(data_loader)))# 测试模型net.eval()with torch.no_grad():correct = 0total = 0for images, labels in test_loader:images = images.view(-1, 28, input_size)outputs = net(images)_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Test Accuracy: {:.2f}%'.format(100 * correct / total))passif __name__ == '__main__':model = RNN(input_size=28, hidden_size=64, num_classes=10)# 加载MNIST数据集train_dataset = datasets.MNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True)test_dataset = datasets.MNIST(root='./data', train=False, transform=transforms.ToTensor())# 定义数据加载器train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=8, shuffle=True)test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=8, shuffle=False)train(model, train_loader, test_loader)可以看到测试精度还是比较高的。
Epoch 1, Loss: 0.6863
Epoch 2, Loss: 0.3386
Epoch 3, Loss: 0.3025
Epoch 4, Loss: 0.2789
Epoch 5, Loss: 0.2924
Epoch 6, Loss: 0.2702
Epoch 7, Loss: 0.2620
Epoch 8, Loss: 0.2580
Epoch 9, Loss: 0.2459
Epoch 10, Loss: 0.2680
Test Accuracy: 93.12%下一篇文章,我们来看看循环神经网络的两种变体,LSTM和GRU。





— Docker架构介绍)










)


