李雅普诺夫稳定性定理

假设系统状态方程：

 零状态为其平衡状态，即f(0,t)=0   t＞t0。如果存在一个具有连续的一阶偏导数的标量函数V (x,t)，并且满足下述条件：

1、V (x,t)是正定的；

2、沿状态方程轨线的V (x,t)是负定的。

则在原点x=0处的平衡状态是逐渐稳定的。

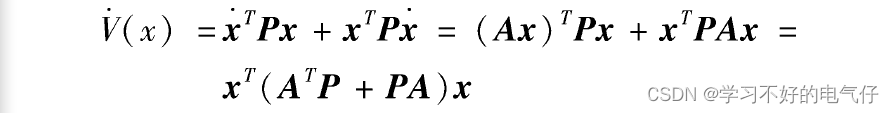
 系统的平衡状态x=0在大范围内逐渐稳定的充分必要条件是:对一个给定的实对称正定矩阵Q，李雅普诺夫矩阵方程存在一个正实对称矩阵解。

具有可调增益的一阶线性系统

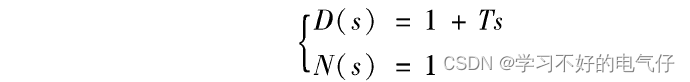
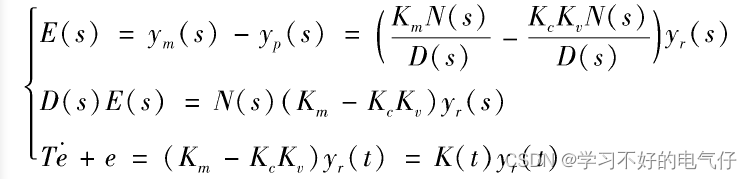
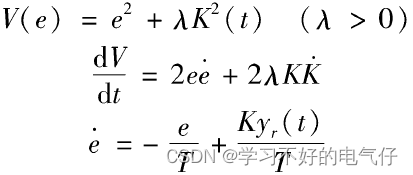
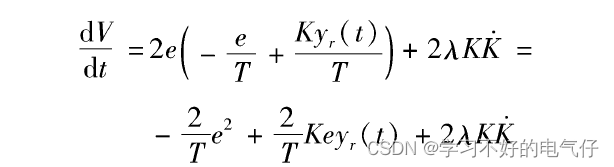
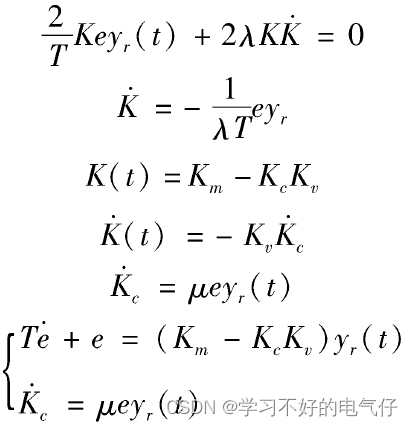
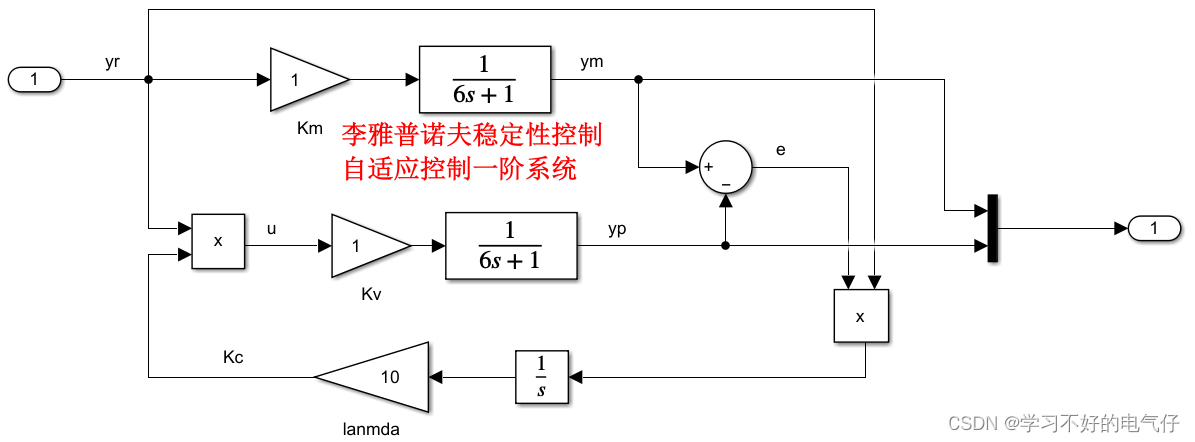
具有可调增益的二阶线性系统

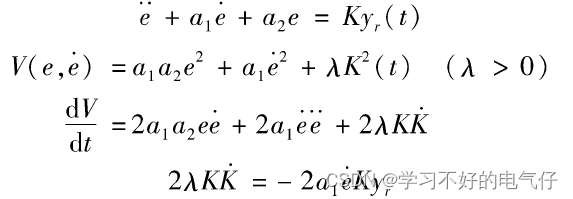
 与一阶系统比较， 的调整规律类似，但e变为了。由此，可以看出基于李雅普诺夫稳定性理论设计模型参考自适应控制系统的基本思路：

1、系统必须稳定；

2、一定可以找出李雅普诺夫函数；

3、以该函数为约束条件或出发点，寻找自适应律。

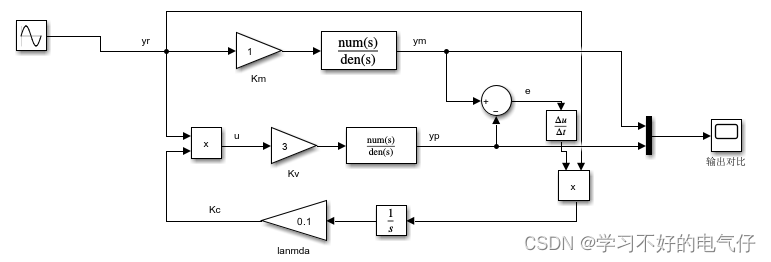
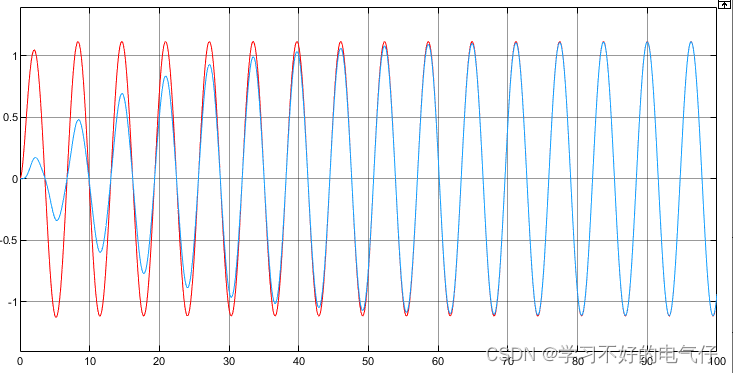
 基于李雅普诺夫稳定性理论设计模型参考自适应控制系统需要注意：
1、能找到李雅普诺夫函数是充分条件，但一时找不到并不说明系统不稳定；
2、该方法的困难在于如何扩大李雅普诺夫函数类，
3、自适应律不仅与e(t)有关，还常常与其各阶导数有关。虽然可以找到与e(t)的导数无关的自适应律，但条件的限制使寻找李雅普诺夫函数更加困难。