**17 **材质与外观
材质与BRDF
自然界中的材质:丝绸、头发、蝴蝶翅膀表面、寿司表面等等
图形学中的材质:同一个模型之所以渲染出不同结果的原因就是因为材质。在图形学中是给不同的物体指定不同的材质,知道它们如何和光线作用后就能正确的渲染。

漫反射 BRDF
漫反射材质:光线打到一个点上后均匀分散到各个不同方向上。

漫反射材质可以定义它在任何一个点上可以有不同的漫反射系数,虽然都是漫反射,但各个点的光被吸收的不同,所以会显示出不同的颜色。
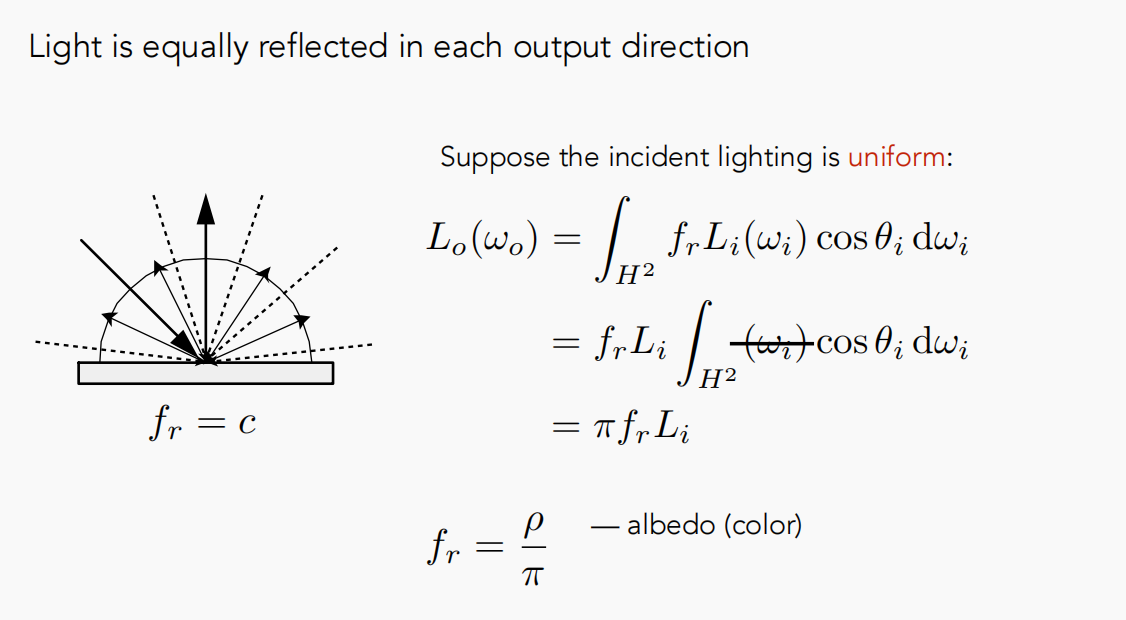

Glossy BRDF

Glossy材质,不完全镜面反射,也就是抛光金属。
BSDF=BRDF+BTDF
折射:一根光线打进来,一部分能量沿着镜面反射出去;有一部分能量却进到物体内部,这叫折射。
这种材质是玻璃或者水。

反射BRDF和折射BTDF共同称为散射BSDF
反射BRDF
反射定律:对于镜面物体有一个入射方向,法线方向,出射方向,入射角等于出射角。
反射公式:
- 平行四边形法则
- 投影
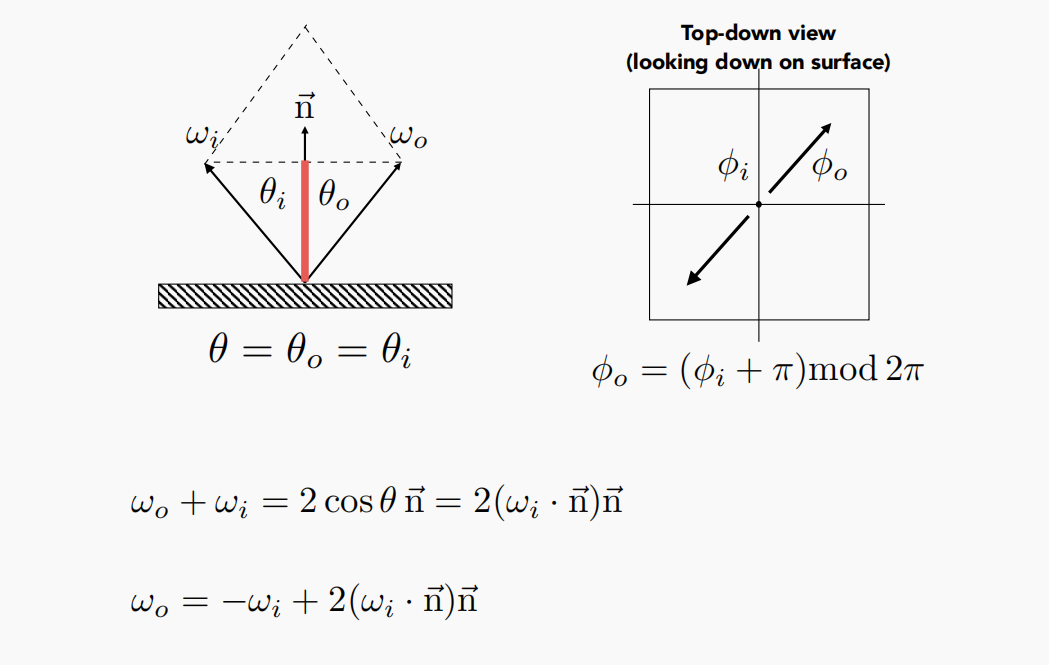
折射BTDF
斯内尔定律:入射角的正弦和折射角的正弦,它们之间满足折射率相乘相等的关系。
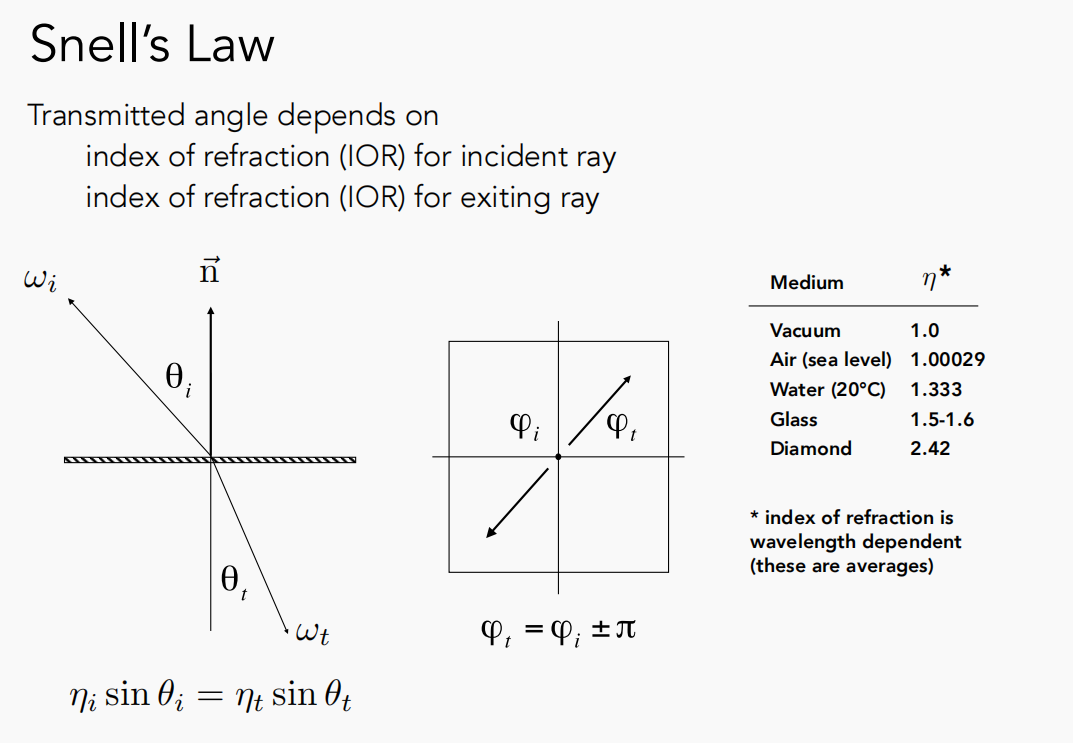
折射角的计算:

折射方向的计算:
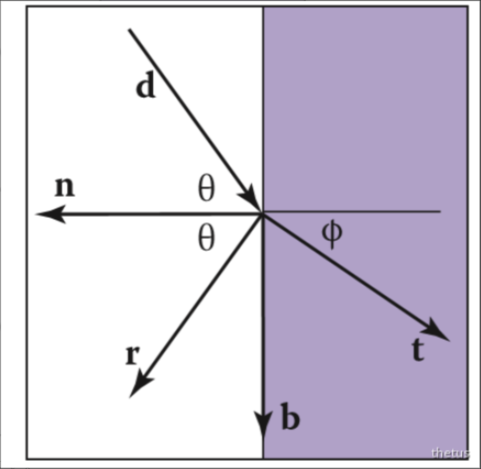

全反射现象BTDF:
再来看折射角公式:

例:
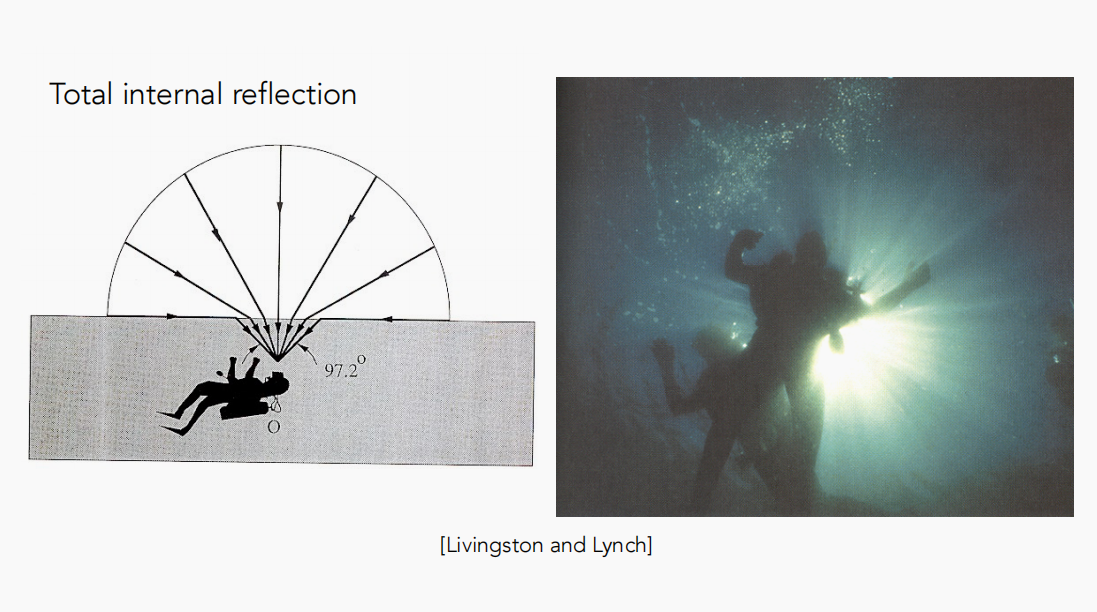
菲涅尔项
日常生活中可以发现,物体的反射率与观察角度有关。

对于绝缘体来说观察角度与法线夹角越大,反射的程度就越大,如下图:
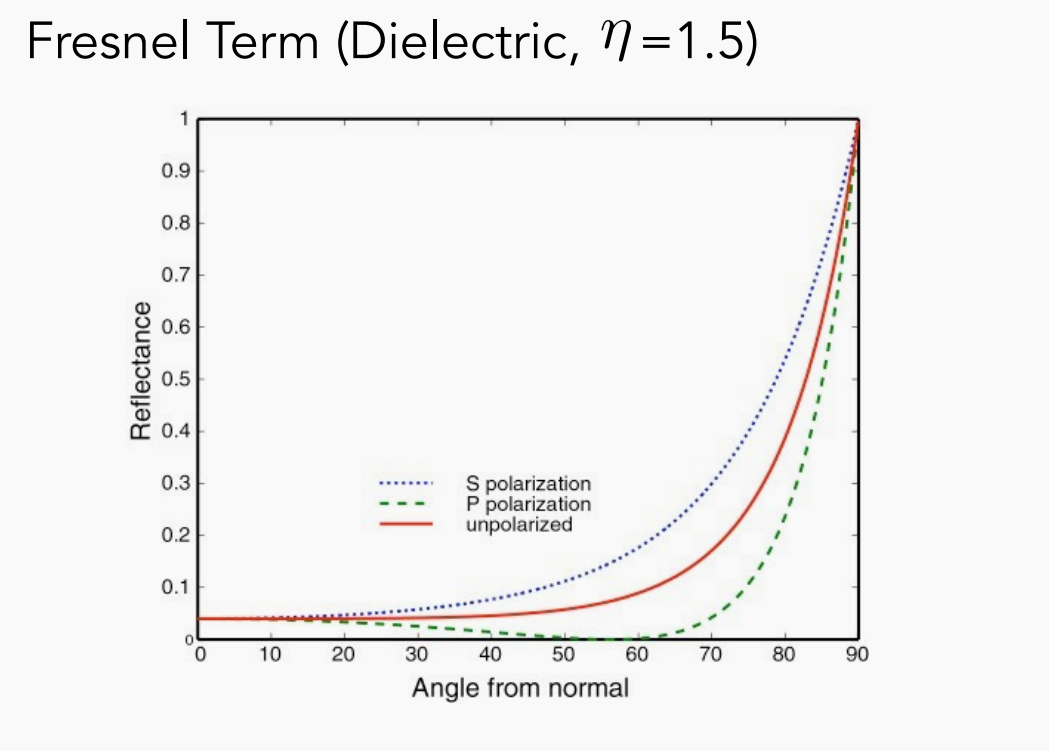
导体(金属)与绝缘体不同,他的反射率与夹角呈如下关系:
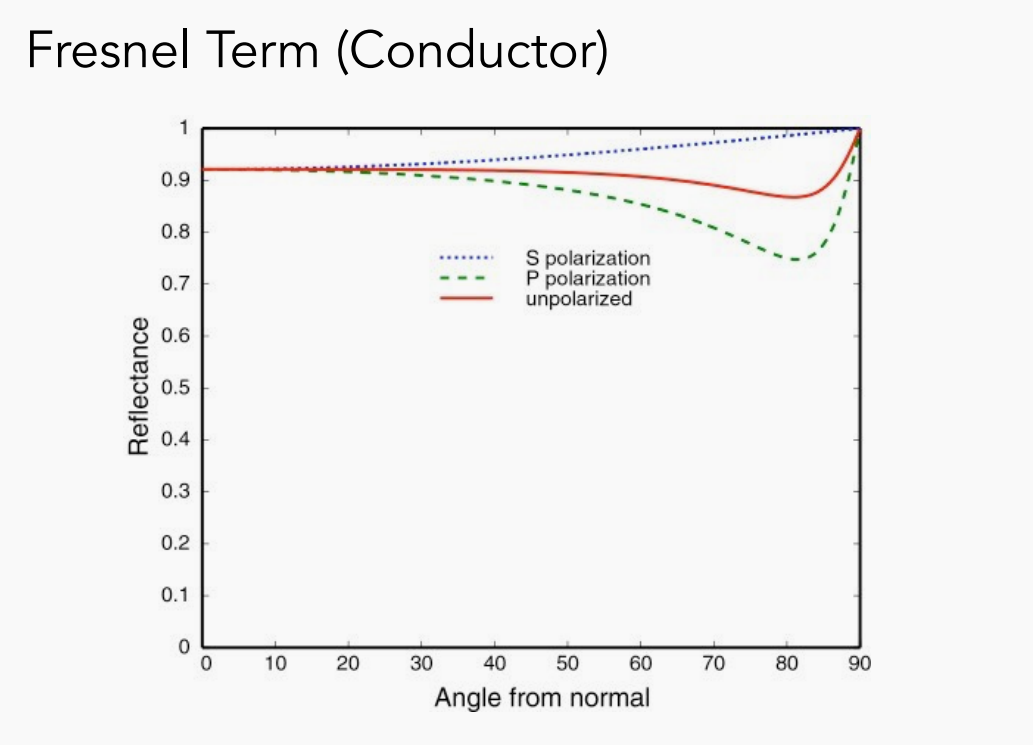
菲涅尔项公式(精确)

微表面理论 Microfacet Material
镜面反射项推导
对于一个物体如果我们离得足够远,很多微小的东西是看不到的,看到的是他们总体对表面的作用。
微平面理论,就是从微观的角度去分析,其认为任意物体的表面在到达微观的尺度之后,都是由许许多多的更小的镜面所组成的:

远处(macrosurface)看材质 近处(microsurface)看几何
微表面BRDF的核心是认为每个微表面都有自己的法向量,它们的分布对整体的法向量有贡献。
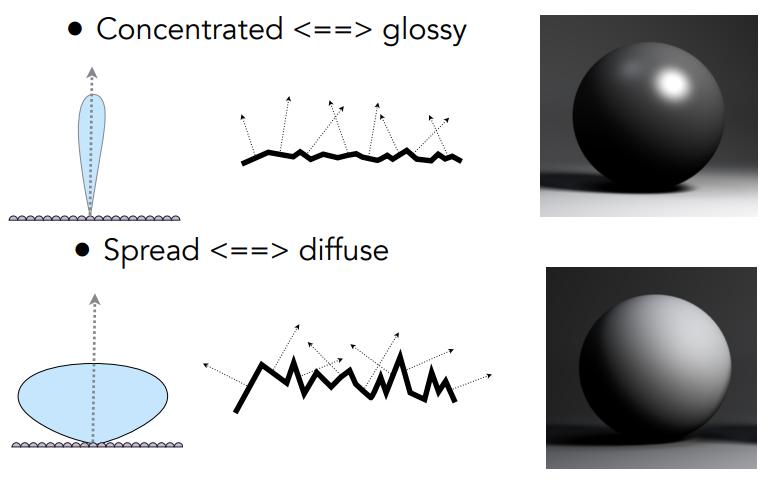
Glossy的微表面法向量分布与整体几乎一致,而diffuse较为分散。
微表面镜面反射项公式
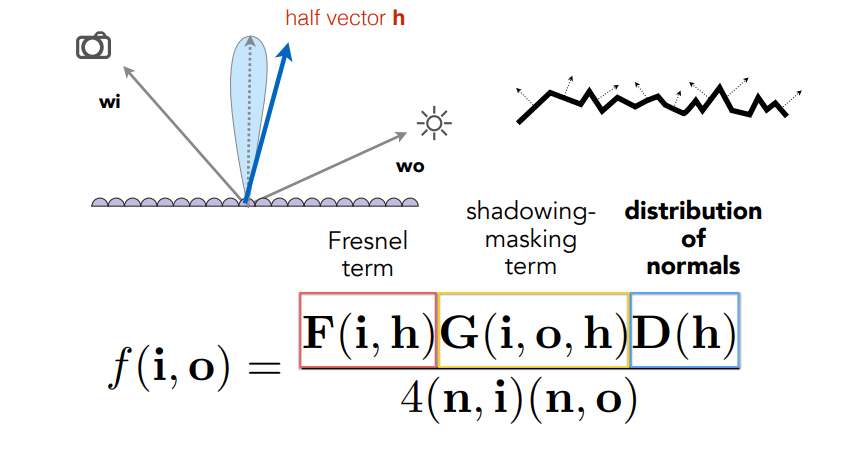




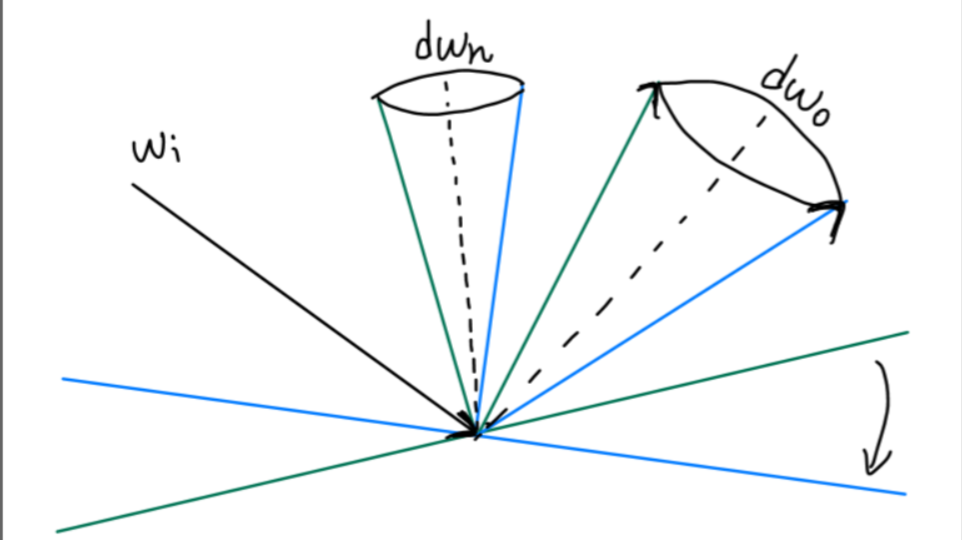

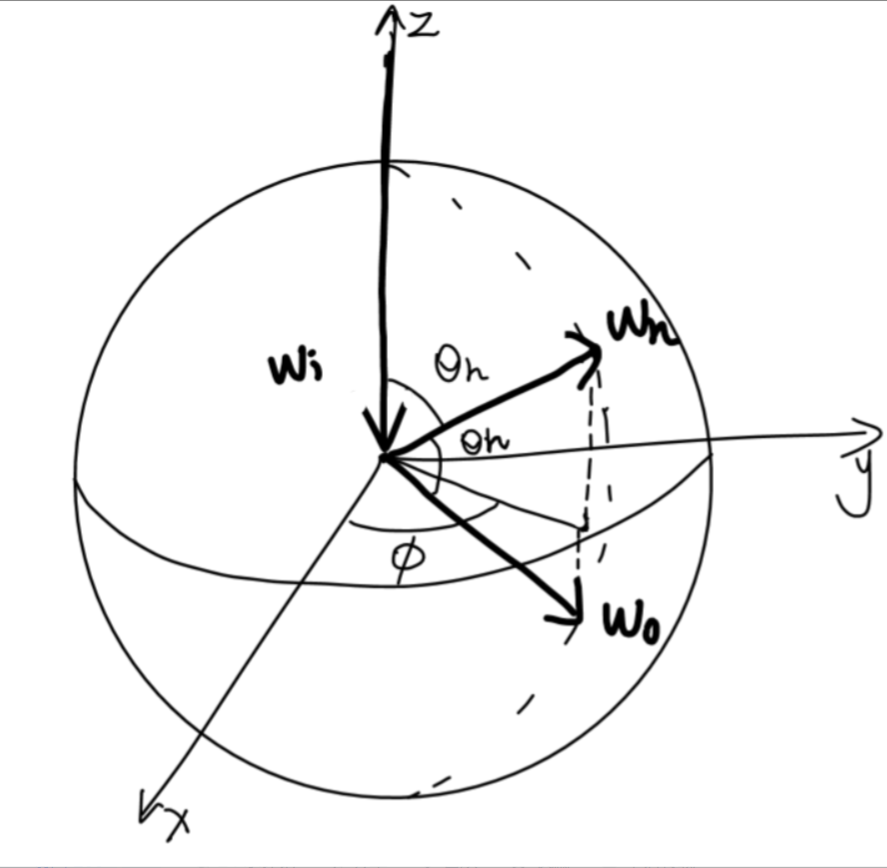


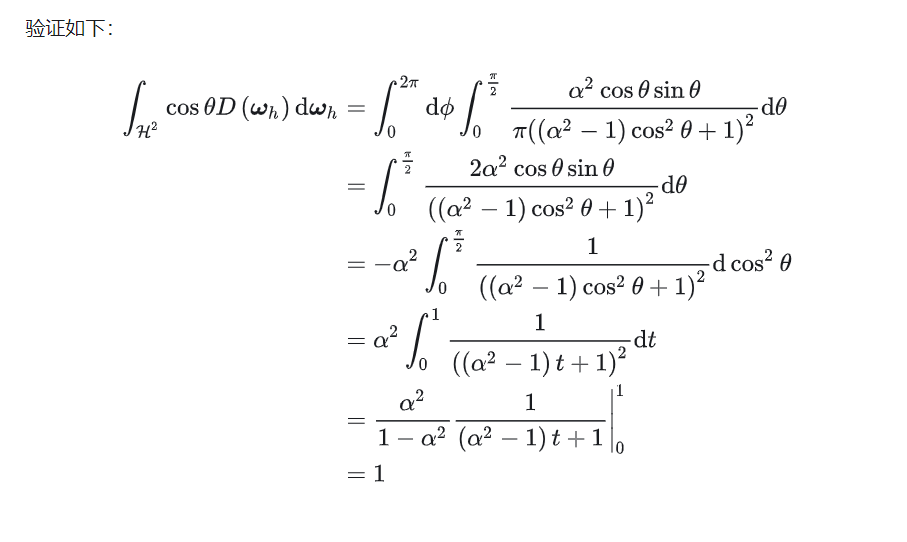
区分材质
材质可以分为两类:
- 各向同性:微表面法线分布均匀
- 各项异性:微表面法线分布有明确的方向性
各项异性的BRDF
- 和方向角(绝对立体角)有关
- 拉丝金属(钢锅底)、尼龙、天鹅绒
BRDFs的性质
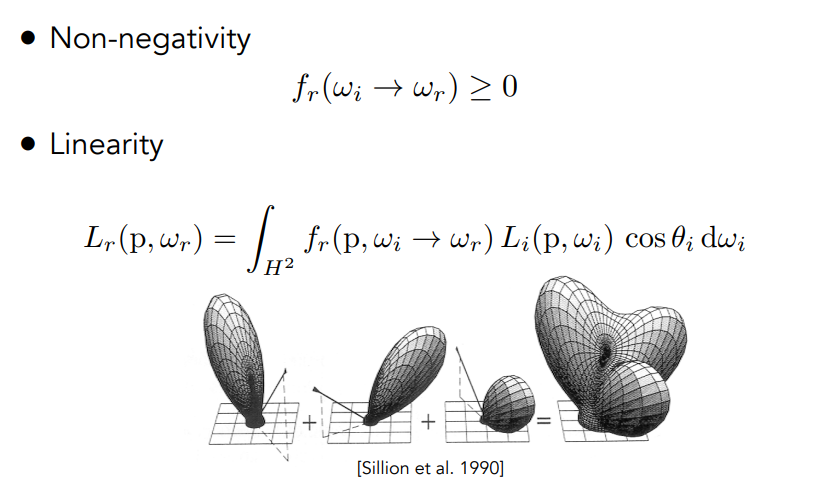
- 非负性:能量的分布
- 线性性质:Blinn-Phong
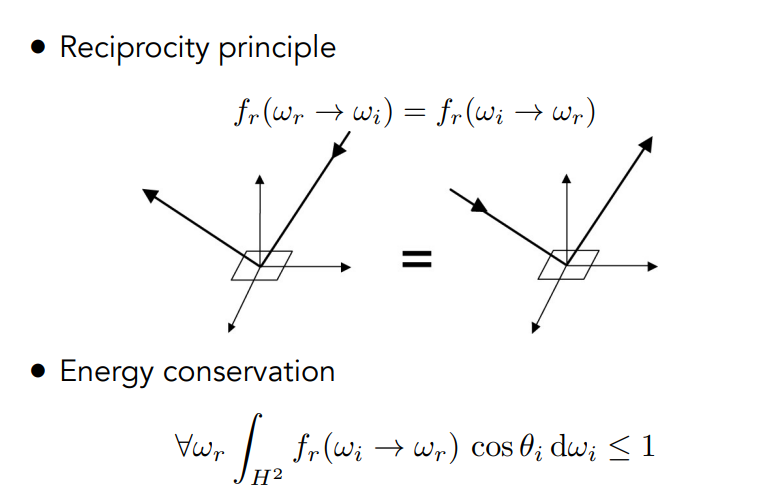
- 可逆性
- 能量守恒
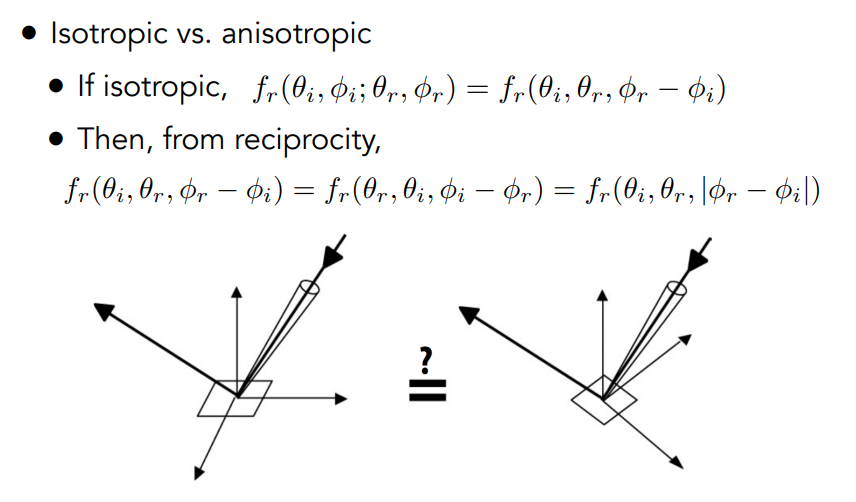
- 各向同性/异性
BRDFs的测量
- 测量的原因:理论准确,直接测出来,能测出来的就不用计算了。
- 做法:枚举所有camera和光源的入射出射方向
- 著名BRDF库:MERL BRDF Database


)
)








)

)



)
)