1. 堆排序

堆排序是一种比较复杂的排序算法，因为它的流程比较多，理解起来不会像冒泡排序和选择排序那样直观。

1.1 堆的结构
要理解堆排序，首先要理解堆。堆的逻辑结构是一棵完全二叉树，物理结构是一个数组。 (如果不知道什么是二叉树，请前往我的主页查看)。所以堆是一个用数组表示的完全二叉树。如图：

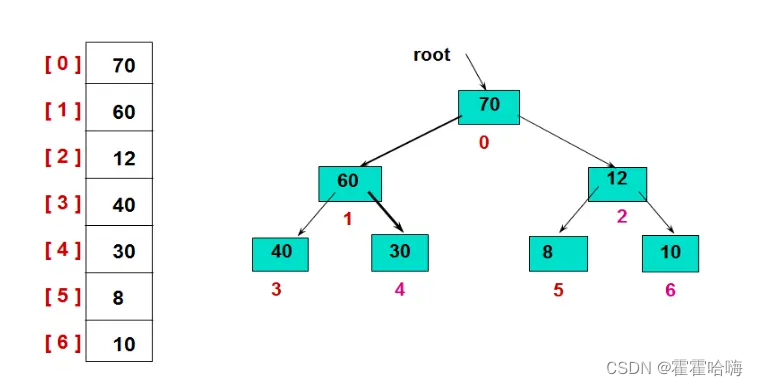
1.2 堆的左右子树与下标的关系

现在的需求是要对数组元素进行排序，所以事实上我们还是通过数组的下标来操纵数组的元素。但是我们已经把数组想象成一棵完全二叉树了，怎么通过二叉树的左右子树来确定数组下标呢？有如下性质：

1. leftchild = parent * 2 + 1
2. rightchild = parent * 2 + 2
3. parent = (child - 1) /2 （child 是左孩子或右孩子）
4. 堆的右子树 = 左子树 + 1

1.3 大堆和小堆的概念

• 大(顶)堆：是指所有父亲节点的值都大于等于孩子节点的值。大堆的堆顶是数组元素的最大值。
• 小(顶)堆：是指所有父亲节点的值都小于等于孩子节点的值。小堆的堆顶是数组元素的最小值。

堆排序主要分三步：
（1）构建堆
（2）调整堆
（3）堆排序

首先需要明确一点，构建堆是在数组基础上构建的，换句话说就是将数组抽象成一个二叉堆，而不是凭空构建。

1.1排序思想

1.首先将待排序的数组构造一个大根堆，此时，整个数组的最大值就是堆结构的顶端。
2.将堆结构内顶端的数与堆的最后一个叶节点所在的数交换，此时，末尾的数为最大值，把它不看作堆里面的了，剩余待排序的个数为n - 1。
3.将剩余的n - 1个数再构造成大根堆，再将堆顶的数与n - 1位置的数交换，如此反复执行，最后就能得到有序数组了。

注意：排升序建大根堆，排降序建小根堆。(默认排升序)

原因：由于堆排序的本质是选数排序，是通过堆来选数的。如果排升序时建小堆，最小的数在堆顶已经被选出来了。那么在剩下的数中再去选数，但是这时剩下的数的父子结构关系都乱了，需要重新建堆才能选出下一个数，建堆的时间复杂度是0(N)，这样堆排序就没有效率优势了。

• 如何构造大堆

想要建大堆，首先要理解向下调整算法，前提是左右子树都是大堆，否则无法使用该算法(如果要建小堆，则使用向下调整算法的前提是左右子树都是小堆)。

算法思路：
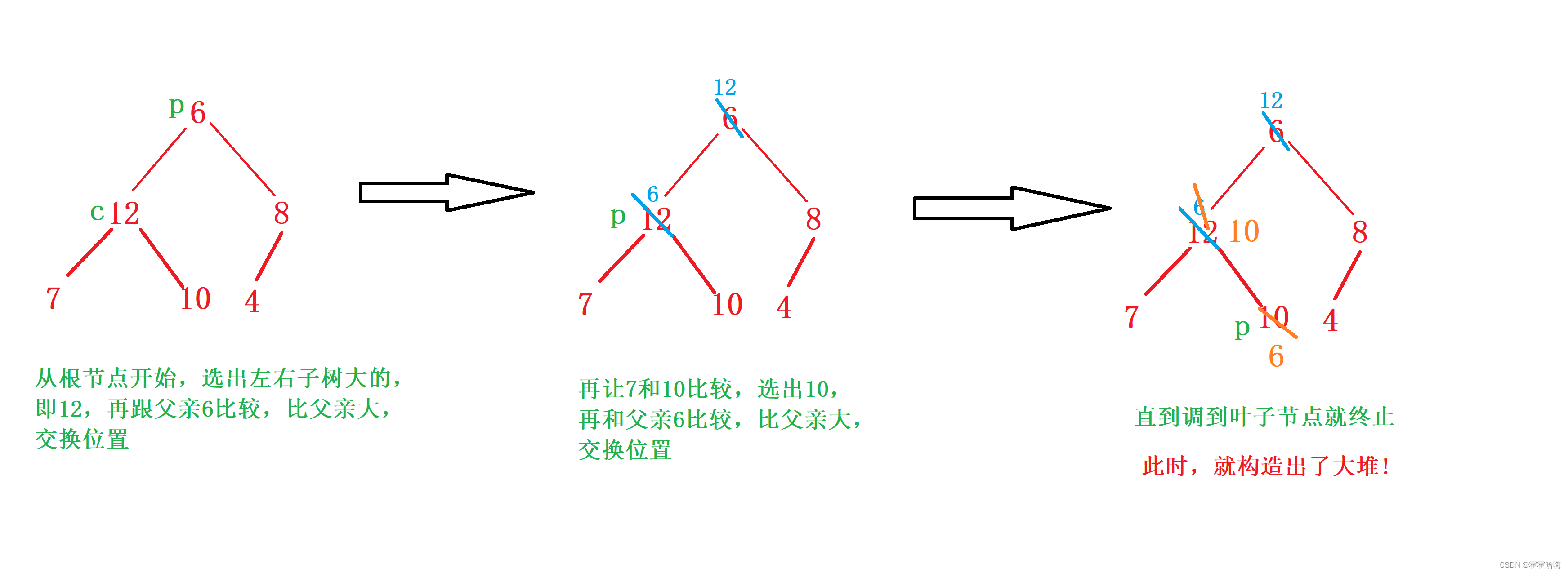
从根节点开始，选出左右孩子中大的那一个，跟父亲比较，如果比父亲大就和父亲交换位置，然后再继续向下调，调到叶节点就终止。

举一个简单的例子解释：

向下调整算法代码实现如下：

注意：第一个if的判断条件中child + 1 < sz 是为了避免左子树存在，而右子树不存在的情况，即计算右子树的下标时数组越界了。

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}//sz是数组元素个数
void AdjustDown(int* arr, int sz, int root)
{int parent = root;int child = parent * 2 + 1;//默认孩子是左孩子while (child <sz){//选出左右孩子中较小的那一个if (child + 1 < sz && arr[child + 1] > arr[child]){child += 1;}if ( arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}

但是我们知道一个任意的数组要满足这个前提是几乎不可能的，那么给定一个无序的序列，该如何利用向下调整算法构建成大堆呢？

首先我们任意给定一个无序的数组，将其看做一个堆结构，一个没有规则的二叉树，将序列里的值按照从上往下，从左到右依次填充到二叉树中。

再经过分析，叶子节点不需要调，因为叶子节点没有左右子树，可以当成大堆。所以应该倒着从最后一个非叶子的子树开始调。 那么最后一个非叶子节点的下标如何计算呢？由上文可知，已知一个孩子的下标，计算其父亲的下标，用 parent = (child - 1) /2即可。如上图，9的下标是4，其父亲6的下标为(4 - 1) / 2 = 1符合。

我们找到了最后一个非叶子节点，即元素值为6的节点，比较它的左右节点中最大的一个的值，是否比他大，如果大就交换位置。
在这里5小于6,而9大于6，则交换6和9的位置；

找到下一个非叶子节点4，用它和它的左右子节点进行比较，4大于3，而4小于9，交换4和9位置；

此时发现4小于5和6这两个子节点，我们需要进行调整，左右节点5和6中，6大于5且6大于父节点4，因此交换4和6的位置；

此时我们就构造出来一个大根堆。代码实现如下：

注意：for循环中的sz - 1是指数组最后一个元素的下标，即最后一个叶子的位置；(sz - 1 - 1) / 2是指最后一个非叶子节点的位置。

void HeapSort(int* arr, int sz)
{//建堆//但是，如果我们要排升序，就要建大堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, sz, i);//建好了大堆}
}

通过上述操作建好了大堆，接下来进行排序

首先将顶点元素9与末尾元素4交换位置，此时末尾数字为最大值。排除已经确定的最大元素，将剩下元素重新构建大根堆。
第一次交换重构如图:

此时元素9已经有序，末尾元素则为4(每调整一次，调整后的尾部元素在下次调整重构时都不能动)。
第二次交换重构如图:

最终排序结果：

排序代码实现如下：

void HeapSort(int* arr, int sz)
{//建堆//但是，如果我们要排升序，就要建大堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, sz, i);//建好了大堆}int end = sz - 1;while (end > 0){//把第一个最大的和最后一个交换，把它不看作堆里的Swap(&arr[0], &arr[end]);//再把前n-1个向下调整成升序，再选出次大的数AdjustDown(arr, end, 0);//end是需要调整的个数，0是根参数，//用的是数组第一个元素的下标end--;}
}

由此，我们可以归纳出堆排序算法的步骤：

1.把无序数组构建成二叉堆。

2.循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

正如上图所示，当我们删除值为9的堆顶节点，经过调节，值为6的新节点就会顶替上来；当我们删除值为6的堆顶节点，经过调节，值为5的新节点就会顶替上来…

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合。

1.4 堆排序的全过程完整代码实现如下：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}//sz是数组元素个数
void AdjustDown(int* arr, int sz, int root)
{int parent = root;int child = parent * 2 + 1;//默认孩子是左孩子while (child <sz){//选出左右孩子中较大的那一个if (child + 1 < sz && arr[child + 1] > arr[child]){child += 1;}if ( arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* arr, int sz)
{//建堆//但是，如果我们要排升序，就要建大堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, sz, i);//建好了大堆}int end = sz - 1;while (end > 0){//把第一个最大的和最后一个交换，把它不看作堆里的Swap(&arr[0], &arr[end]);//再把前n-1个向下调整成升序，再选出次大的数AdjustDown(arr, end, 0);//end是需要调整的个数，0是根参数，//用的是数组第一个元素的下标end--;}
}

排序结果是：

1.5堆排序的时间复杂度：0(N*logN)，是不稳定的排序。

2. 选择排序

选择排序是所有排序算法中最简单的，最容易理解的，同时也是效率极差的排序，几乎不用。

2.1 排序思想：

遍历一个无序数组，一次选出最大值和最小值，再把这两个值分别放到最前和最后的位置；重复这个操作，选出次大值，次小值，分别放到数组的第二个位置和倒数第二个位置……

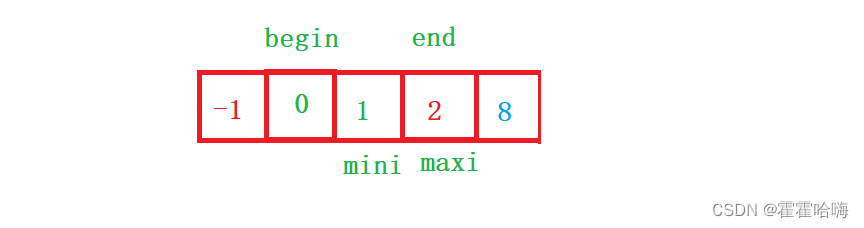
图解如下：(默认排升序)

begin ，end，maxi，mini存放的都是下标。让begin指向第一个元素，end指向最后一个元素，通过遍历数组，在begin和end区间内找到最大值8，下标maxi = 2，最小值-1，下标mini = 3

再让最大值和最小值分别与end，begin位置上的数交换，这样最小的就排在最前面，最大的就排在最后面了，再begin++，end–，在新区间内找到最大值和最小值

再次交换后，就得到了有序数组。

2.2 代码的实现如下：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* arr, int sz)
{int begin = 0;int end = sz - 1;while (begin < end){int maxi = begin;int mini = end;//循环找出当前数中的最大数和最小数for (int i = begin; i <= end; i++){if (arr[i] > arr[maxi]){maxi = i;}if (arr[i] < arr[mini]){mini = i;}}//让最大值和最小值分别与end，begin位置上的数交换Swap(&arr[begin], &arr[mini]);Swap(&arr[end], &arr[maxi]);begin++;end--;}
}

2.3 代码的优化：

但是上述代码有Bug！如果begin和maxi位置上的数重叠，交换时就会发生混乱！图解如下：

maxi和end位置上的数交换后，把最小值换走了，此时最大值放在了最小值的位置上，如果begin再和mini位置上的数交换，排序就会出错！

代码优化如下：

void SelectSort(int* arr, int sz)
{int begin = 0;int end = sz - 1;while (begin < end){int maxi = begin;int mini = end;//循环找出当前数中的最大数和最小数for (int i = begin; i <= end; i++){if (arr[i] > arr[maxi]){maxi = i;}if (arr[i] < arr[mini]){mini = i;}}Swap(&arr[begin], &arr[mini]);//如果begin和maxi位置上的数重叠，就要修正一下maxi的位置if (begin == maxi){maxi = mini;}Swap(&arr[end], &arr[maxi]);begin++;end--;}
}

排序结果如图：

2.4 时间复杂度和稳定性

由于两个循环执行的次数大致都是N次(N为数组元素的个数)，所以选择排序的时间复杂度为0(N*N)，就算是最好的情况下，数组有序，时间复杂度也是0(N * N),选择排序是不稳定的排序。

3. 堆排序和选择排序的性能比较

clock() 函数是 <time.h> 头文件中的一个函数，用来返回程序启动到函数调用时之间的CPU时钟周期数。这个值通常用来帮助衡量程序或程序的某个部分的性能

我们可以用这个函数进一步对比两种排序占用的CPU时间

代码实现为：

// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a3[i] = a1[i];a4[i] = a1[i];}int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);free(a3);free(a4);}int main()
{TestOP();return 0;
}

这里随机生成十万个随机数，分别用希尔排序和直接插入排序来进行排序，测试两种算法的执行时间：

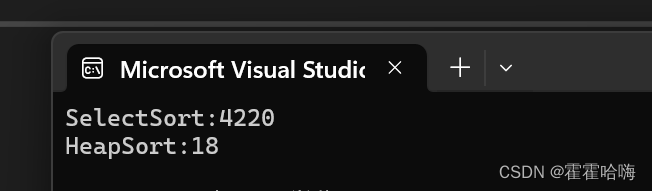
由执行结果可知，堆排序的效率远远高于选择排序。选择排序真的很差！