文章目录
- 1、神经网络监督学习
- 2、深度学习兴起原因
- 3、深度学习二元分类
- 4、深度学习Logistic 回归
- 5、Logistic 回归损失函数
- 6、深度学习梯度下降法
- 7、深度学习向量法
- 8、Python 中的广播
- 9、上述学习总结
- 10、大作业实现:rocket::rocket:
- (1)训练初始数据
- (2)查看训练集信息
- (3)实现显示图片
- (4)前向传播推导
- (5)数据维度处理
- (6)标准化数据
- (7) 反向传播过程推导
- (8)代价函数 梯度下降实现
- (9)预测图片 完结:rose::rose:
- (10)大作业实现总结
参考文档🔥
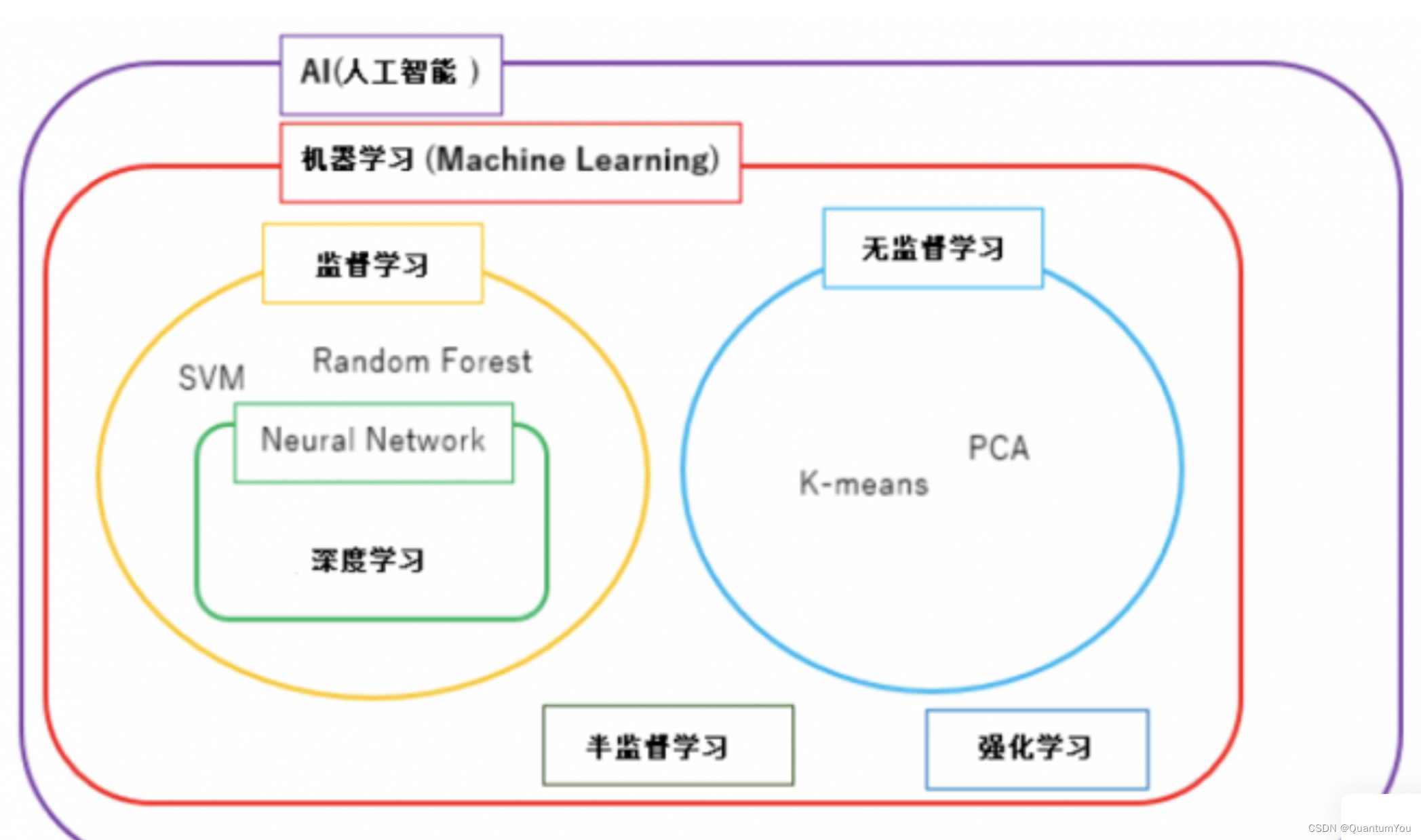
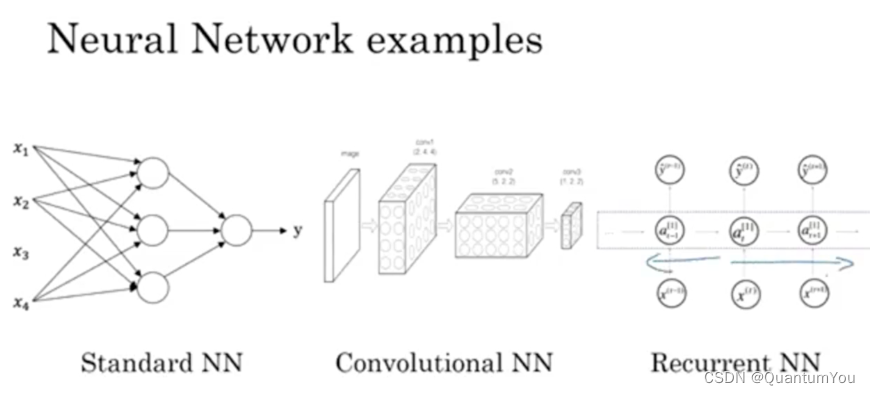
1、神经网络监督学习
- 房地产和在线广告 相对的
标准神经网络 - 图像应用 神经网络上使用卷积(
CNN) - 序列数据 音频,有一个时间组件,随着时间的推移,音频被播放出来,所以音频是最自然的表现。作为一维时间序列(两种英文说法one-dimensional time series / temporal sequence).对于序列数据,经常使用
RNN,一种递归神经网络(Recurrent Neural Network),语言,英语和汉语字母表或单词都是逐个出现的,所以语言也是最自然的序列数据,因此更复杂的RNNs版本经常用于这些应用。
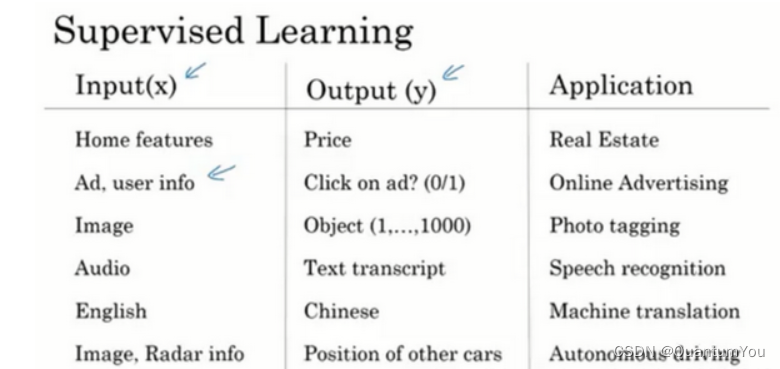
下面为监督学习的常见应用
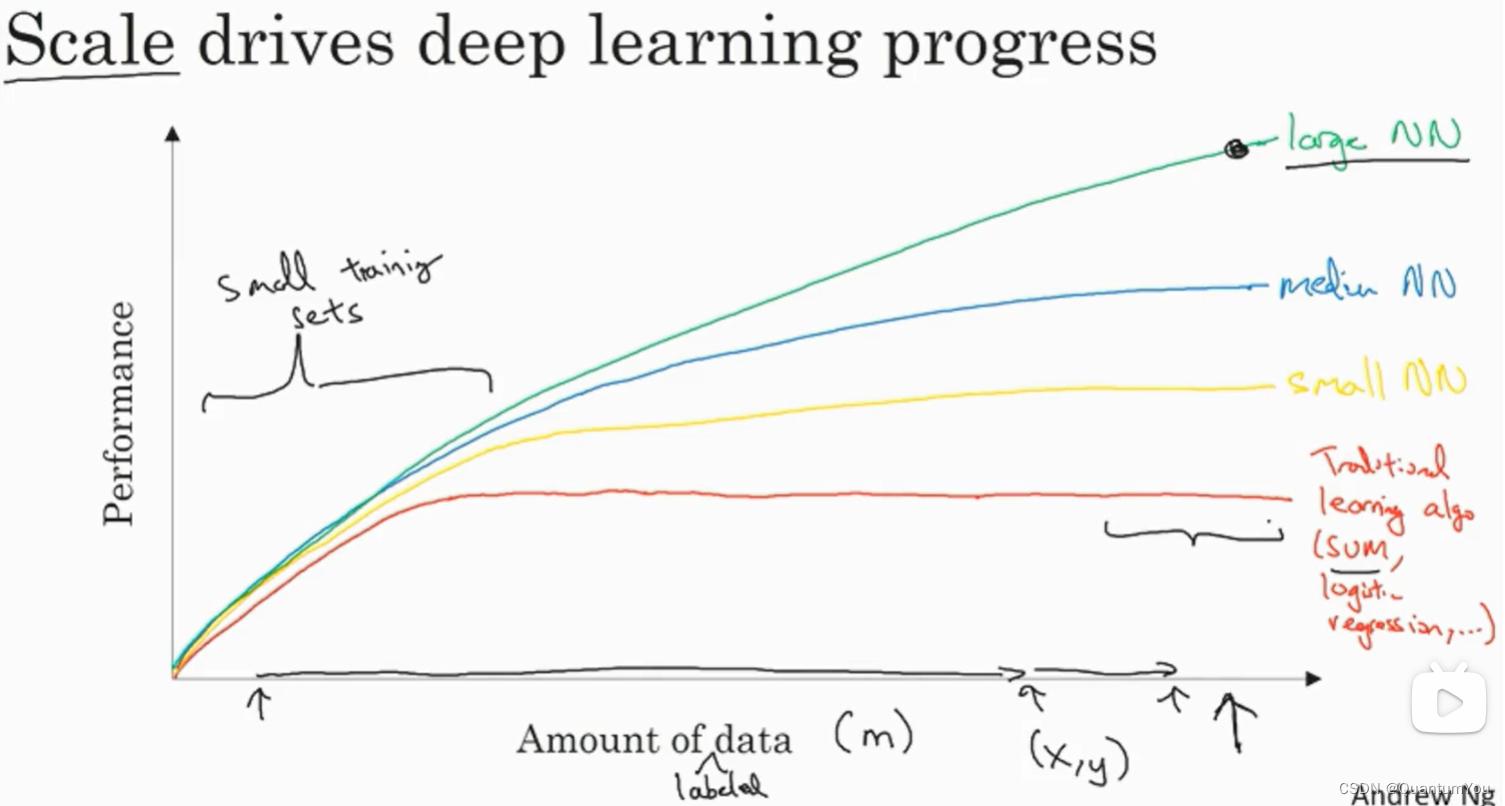
2、深度学习兴起原因
- 在小的训练集中,各种算法的优先级事实上定义的也不是很明确,所以如果没有大量的训练集,那效果会取决于你的特征工程能力,那将决定最终的性能。
- 假设有些人训练出了一个
SVM(支持向量机)表现的更接近正确特征,然而有些人训练的规模大一些,可能在这个小的训练集中SVM算法可以做的更好。 - 因此下面图形区域的左边,各种算法之间的优先级并不是定义的很明确,最终的性能更多的是取决于
工程选择特征方面的能力以及算法处理方面的一些细节,只是在某些大数据规模非常庞大的训练集,也就是在右边这个m会非常的大时,我们能更加持续地看到更大的由神经网络控制的其它方法。
- 神经网络方面的一个巨大突破是从
sigmoid函数转换到一个ReLU函数
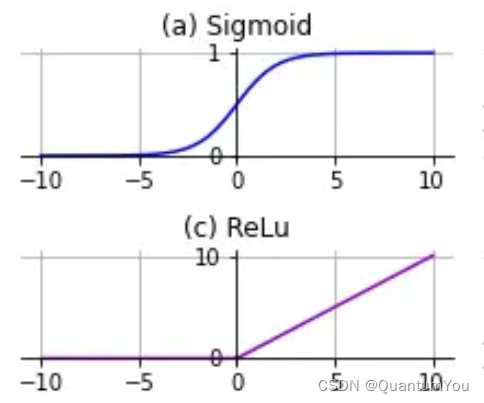
- 使用
sigmoid函数和机器学习问题是sigmoid函数的梯度会接近零,所以学习的速度会变得非常缓慢,因为当实现梯度下降以及梯度接近零的时候,参数会更新的很慢,所以学习的速率也会变的很慢,而通过改变这个被叫做激活函数的东西,神经网络换用这一个函数,叫做ReLU的函数(修正线性单元),ReLU它的梯度对于所有输入的负值都是零,因此梯度更加不会趋向逐渐减少到零。 - 而这里的梯度,这条线的斜率在这左边是零,仅仅通过将
Sigmod函数转换成ReLU函数,便能够使得一个叫做梯度下降(gradient descent)的算法运行的更快
3、深度学习二元分类
- 逻辑回归是一个用于
二分类(binary classification)的算法。 - 假如有一张图片作为输入,比如一只猫,如果识别这张图片为猫,则输出标签
1作为结果;如果识别出不是猫,那么输出标签0作为结果。现在我们可以用字母 来 表示输出的结果标签,如下图所示:
符号定义

4、深度学习Logistic 回归


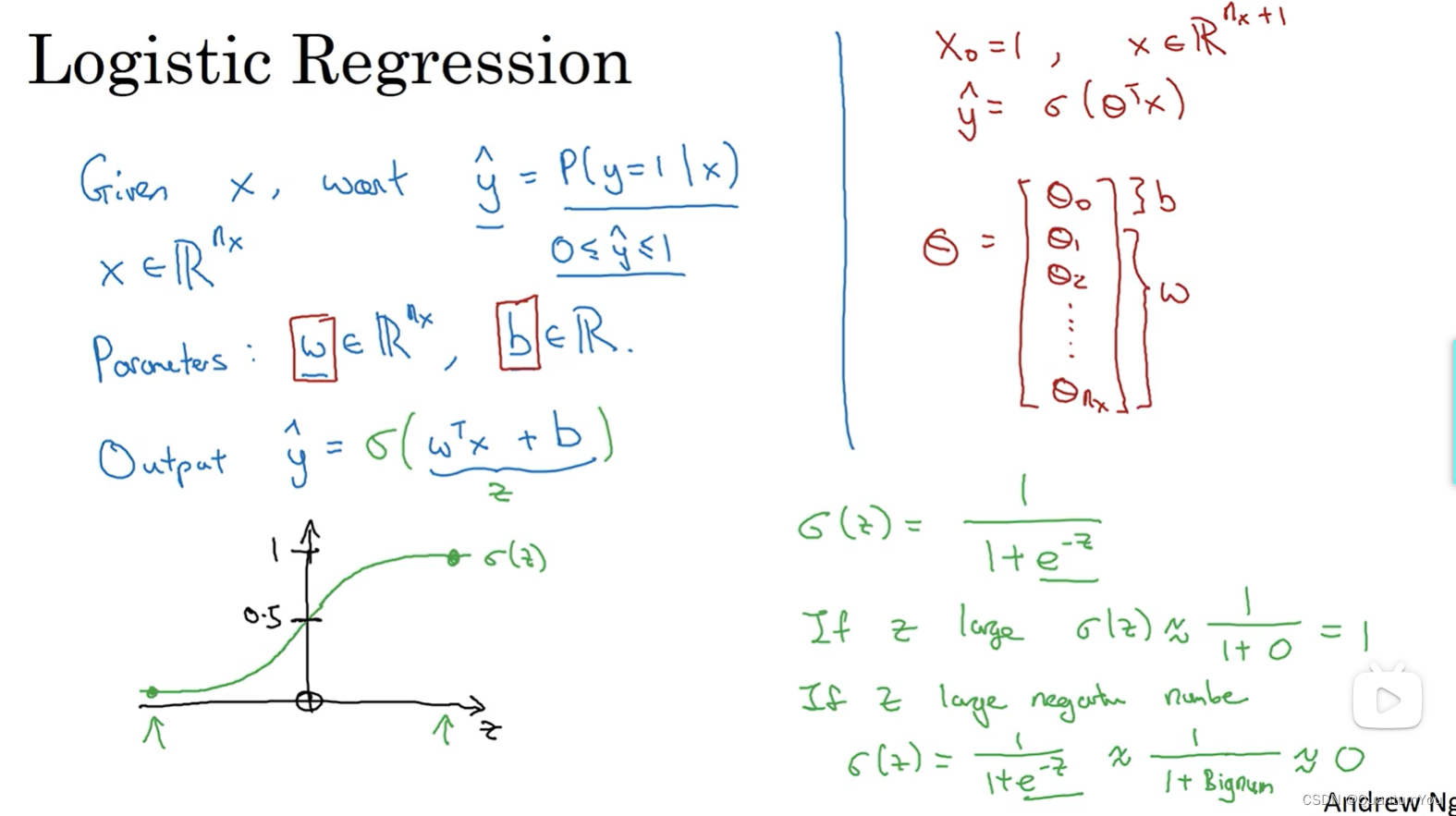
5、Logistic 回归损失函数
- 为了训练逻辑回归模型的参数
w和参数b,我们需要一个代价函数,通过训练代价函数来得到参数w和参数b。先看一下逻辑回归的输出函数:
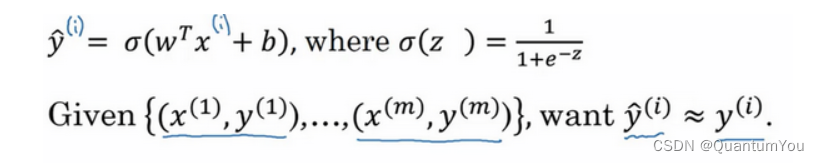
- 为了让模型通过学习调整参数,你需要给予一个
m样本的训练集,这会让你在训练集上找到参数w和参数b,来得到你的输出。

损失函数 - 损失函数又叫做误差函数,用来衡量算法的运行情况
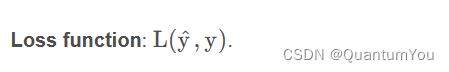
- 我们通过这个称为
L的损失函数,来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做,因为当我们在学习逻辑回归参数的时候,会发现我们的优化目标不是凸优化(要求目标函数为凸函数,且定义域为凸集。这类问题具有很好的性质,使得它们可以通过有效的算法找到全局最优解),只能找到多个局部最优值,梯度下降法很可能找不到全局最优值,虽然平方差是一个不错的损失函数,但是我们在逻辑回归模型中会定义另外一个损失函数。
我们在逻辑回归中用到的损失函数是:
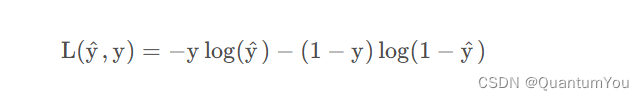

- 上面公式
J为成本函数 - 损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的
w和b,来让代价函数J的总代价降到最低。 根据我们对逻辑回归算法的推导及对单个样本的损失函数的推导和针对算法所选用参数的总代价函数的推导,结果表明逻辑回归可以看做是一个非常小的神经网络。
损失函数 是衡量单一训练样例的效果
成本函数 是用于衡量参数w和b的效果
6、深度学习梯度下降法
- 梯度下降法可以做什么?

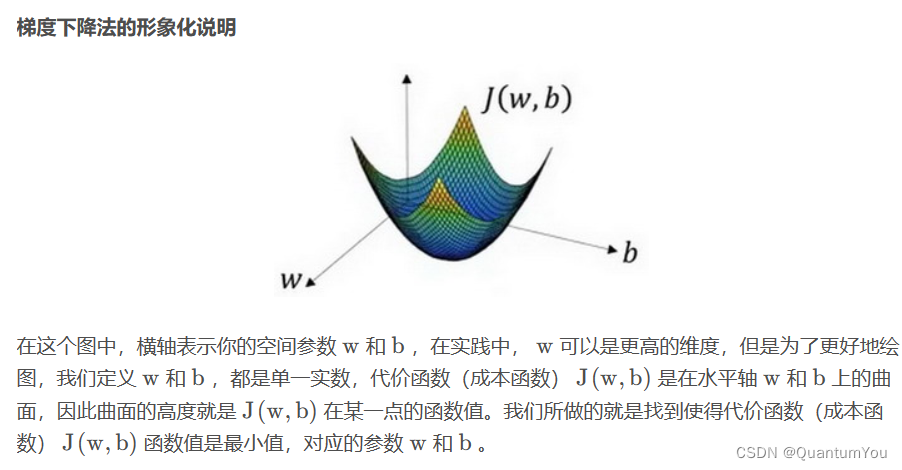
梯度下降法的细节化说明(两个参数):=表示更新参数,


- 反向传播的核心机制就是
链式法则
计算过程推导




m 个样本的梯度下降

J=0;dw1=0;dw2=0;db=0; #初始化
for i = 1 to mz(i) = wx(i)+b;a(i) = sigmoid(z(i));J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));dz(i) = a(i)-y(i);dw1 += x1(i)dz(i);dw2 += x2(i)dz(i);db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
7、深度学习向量法
- 向量化是非常基础的去除代码中
for循环的艺术,在深度学习安全领域、深度学习实践中,你会经常发现自己训练大数据集,因为深度学习算法处理大数据集效果很棒,所以你的代码运行速度非常重要,否则如果在大数据集上,你的代码可能花费很长时间去运行,你将要等待非常长的时间去得到结果。所以在深度学习领域,运行向量化是一个关键的技巧
x
z=0
for i in range(n_x)z+=w[i]*x[i]
z+=b
===================================================
z=np.dot(w,x)+b
- 大规模的深度学习使用了
GPU或者图像处理单元实现”,但是我做的所有的案例都是在jupyter notebook上面实现,这里只有CPU,CPU和GPU都有并行化的指令,他们有时候会叫做SIMD指令,这个代表了一个单独指令多维数据,这个的基础意义是,如果你使用了built-in函数,像np.function或者并不要求你实现循环的函数,它可以让python的充分利用并行化计算,这是事实在GPU和CPU上面计算,GPU更加擅长SIMD计算,但是CPU事实上也不是太差,可能没有GPU那么擅长吧。接下来的视频中,你将看到向量化怎么能够加速你的代码,经验法则是,无论什么时候,避免使用明确的for循环
n指的是X的行数,也就是单一一个输入的维度,而X则是所有的输入,m为输入的个数


向量化 Logistic 回归的梯度输出

- 去除for 循环前后对比

8、Python 中的广播
-
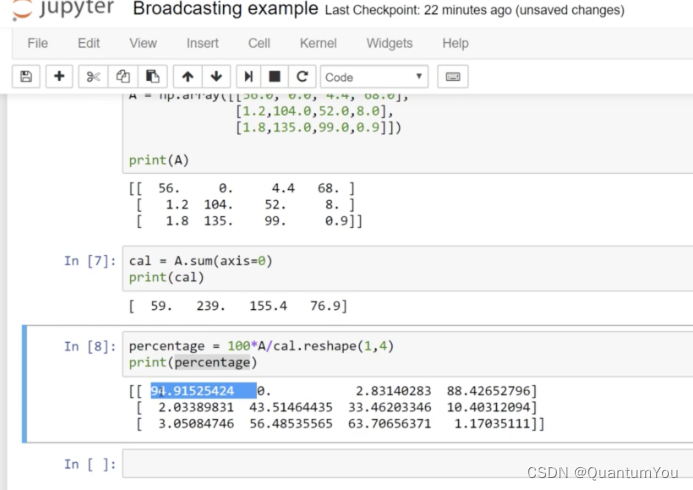
下面再来解释一下
A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行。 -
而第二个
A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用3 ∗ 4的矩阵 A 除以1 ∗ 4的矩阵cal。技术上来讲,其实并不需要再将矩阵cal reshape(重塑)成1 ∗ 4,因为矩阵cal本身已经是1 ∗ 4了。但是当我们写代码时不确定矩阵维度的时候,通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作reshape是一个常量时间的操作。
9、上述学习总结
(1)第一题
神经元计算什么?神经元计算一个线性函数(z=Wx+b),然后接一个激活函数
(2)第二题
- 逻辑回归的
损失函数?
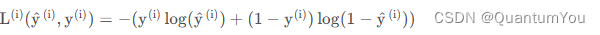
(3)第三题
- 考虑以下两个随机数组a和b:
a = np.random.randn(2, 3) # a.shape = (2, 3)
b = np.random.randn(2, 1) # b.shape = (2, 1)
c = a + bc的维度是什么?
A.c.shape = (3, 2)
B.c.shape = (2, 1)
C.c.shape = (2, 3)(√)
D.计算不成立因为这两个矩阵维度不匹配
解:a和b的形状不同,会触发广播机制,b将元素进行复制到(2, 3),c的形状为(2, 3)
(4)第四题
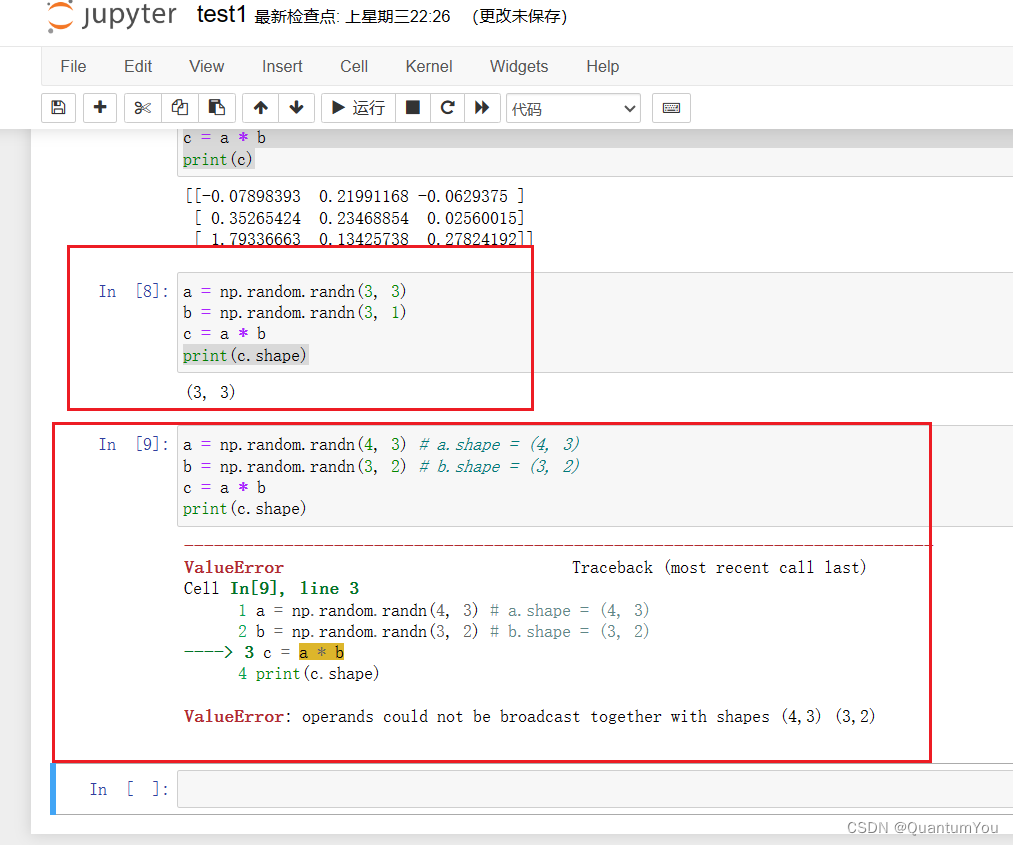
- 考虑以下两个随机数组a和b:
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b
c的维度是什么?
A.c.shape = (4, 3)
B.c.shape = (3, 3)
C.c.shape = (4, 2)
D.计算不成立因为这两个矩阵维度不匹配(√)
(5)第五题
np.dot(a,b)对a和b的进行矩阵乘法,而a*b执行元素的乘法,考虑以下两个随机数组a和b:
a = np.random.randn(12288, 150) # a.shape = (12288, 150)
b = np.random.randn(150, 45) # b.shape = (150, 45)
c = np.dot(a, b)
c的维度是什么?
A.c.shape = (12288, 150)
B.c.shape = (150, 150)
C.c.shape = (12288, 45)
D.计算不成立因为这两个矩阵维度不匹配
解:(12288, 45), (m, n)的矩阵与(n, l)的矩阵相乘,结果为(m, l)的矩阵
(6)第六题
-
在Python中,
for i in range(3):是一个循环语句,它会创建一个循环,变量 i 会依次取range(3)生成的序列中的值。range(3) 生成的是一个从0开始到2的整数序列(包括0,不包括3),因此 i 会依次取值0, 1, 2。 -
np.random.randn(12288, 150)是一个NumPy库中的函数调用,用于生成一个形状为(12288, 150)的随机数数组。这个数组中的元素是从标准正态分布(均值为0,标准差为1)中随机抽取的。
请考虑以下代码段:
a.shape = (3,4)
b.shape = (4,1)
for i in range(3):for j in range(4):c[i][j] = a[i][j] + b[j]
如何将之矢量化?
A.c = a + b
B.c = a +b.T
C.c = a.T + b.T
D.c = a.T + b
import numpy as np# 定义矩阵a和b
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
b = np.array([[1], [2], [3], [4]])# 初始化矩阵c
c = np.zeros((3, 4))# 执行矩阵相加操作
for i in range(3):for j in range(4):c[i][j] = a[i][j] + b[j]print(c)
[[ 2. 3. 4. 5.][ 7. 8. 9. 10.][12. 13. 14. 15.]](7)第七题
- 维度兼容:如果两个数组从尾部开始比对时,对应维度的大小一致,或者其中一个数组在该维度上的大小为1,则这两个数组在那个维度上是兼容的。
请考虑以下代码段:
a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b
c的维度是什么?
A.这会触发广播机制,b会被复制3次变成(3 * 3),而 * 操作是元素乘法,所以c.shape = (3, 3)
B.这会触发广播机制,b会被复制3次变成(3 * 3),而 * 操作是矩阵乘法,所以c.shape = (3, 3)
C.这个操作将一个3x3矩阵乘以一个3x1的向量,所以c.shape = (3, 1)
D.这个操作会报错,因为你不能用*对这两个矩阵进行操作,你应该用np.dot(a, b)
注意与第四题的区别!!
10、大作业实现🚀🚀
在开始之前,我们有需要引入的库:
numpy:是用Python进行科学计算的基本软件包。h5py:是与H5文件中存储的数据集进行交互的常用软件包。matplotlib:是一个著名的库,用于在Python中绘制图表。lr_utils:在本文的资料包里,一个加载资料包里面的数据的简单功能的库。
(1)训练初始数据
# 训练原始数据 注意|| 转译
train_data = h5py.File('C:\\Users\\Administrator\\Desktop\\week2\\datasets\\train_catvnoncat.h5','r')
train_test = h5py.File('C:\\Users\\Administrator\\Desktop\\week2\\datasets\\test_catvnoncat.h5','r')

(2)查看训练集信息
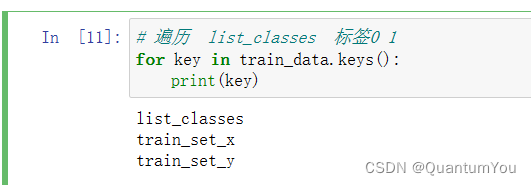
参数说明
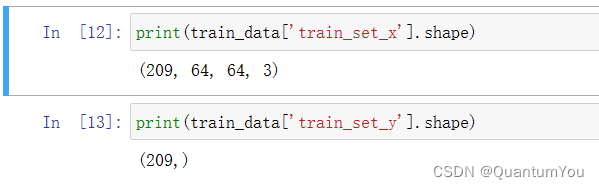
- 保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
取出训练集 测试集 [:] 取出所有数据集
注意文件操作[]
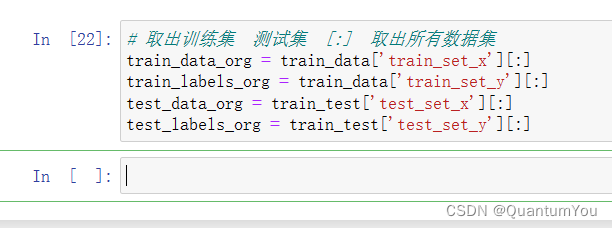
# 取出训练集 测试集 [:] 取出所有数据集
train_data_org = train_data['train_set_x'][:]
train_labels_org = train_data['train_set_y'][:]
test_data_org = train_test['test_set_x'][:]
test_labels_org = train_test['test_set_y'][:]
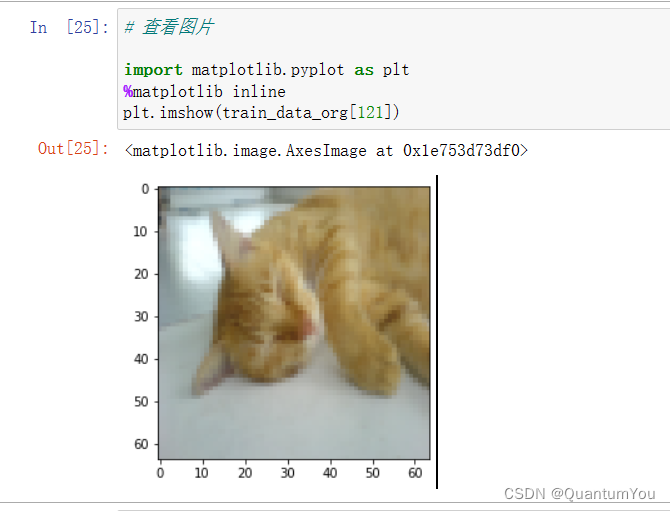
(3)实现显示图片
# 查看图片import matplotlib.pyplot as plt
%matplotlib inline
plt.imshow(train_data_org[121])
(4)前向传播推导
- 本人手写,字丑勿喷😢😢


(5)数据维度处理
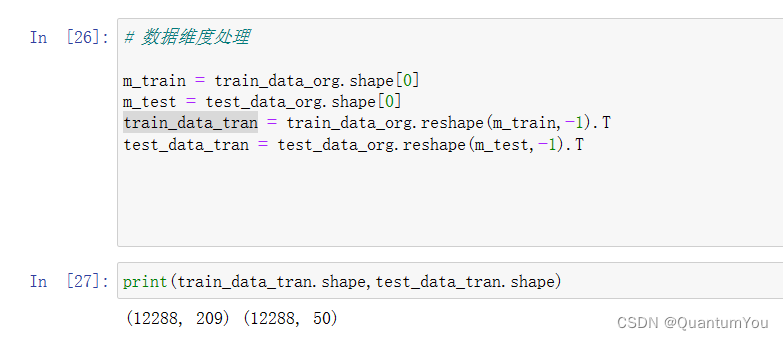
# 数据维度处理m_train = train_data_org.shape[0]
m_test = test_data_org.shape[0]
train_data_tran = train_data_org.reshape(m_train,-1).T
test_data_tran = test_data_org.reshape(m_test,-1).T
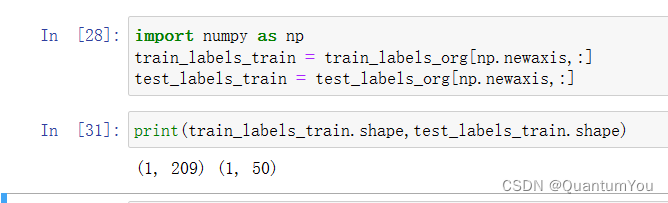
转化标签列,与(4)推导过程相同
import numpy as np
train_labels_train = train_labels_org[np.newaxis,:]
test_labels_train = test_labels_org[np.newaxis,:]
(6)标准化数据
- 数据进行归一化
x - min /(max - min )
标准化 数据前后的区别(-1~1之间)
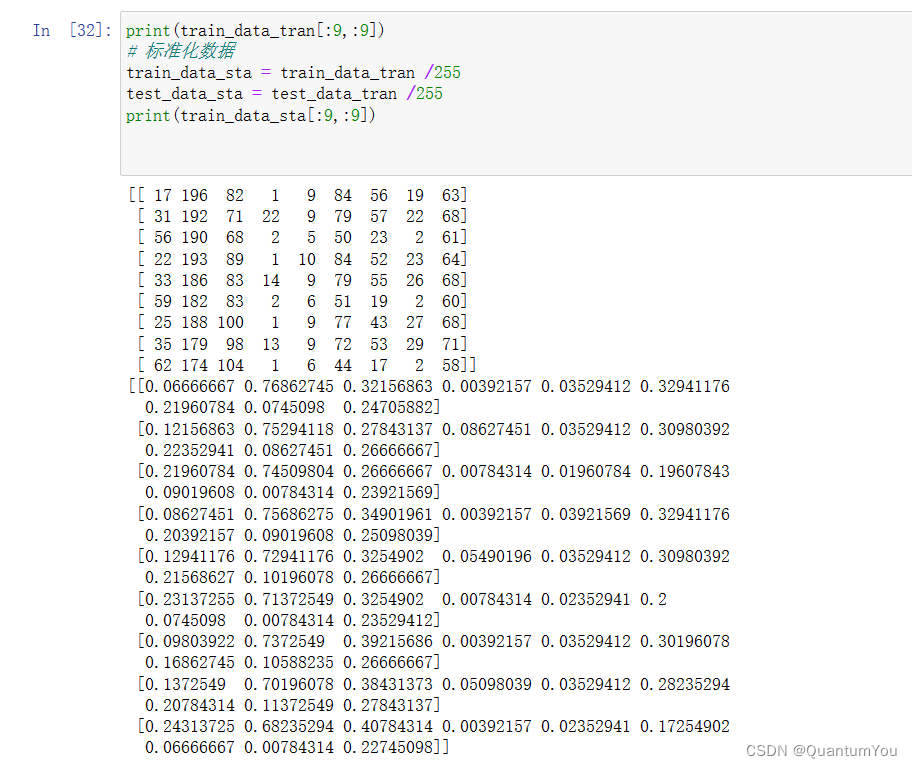
print(train_data_tran[:9,:9])
# 标准化数据
train_data_sta = train_data_tran /255
test_data_sta = test_data_tran /255
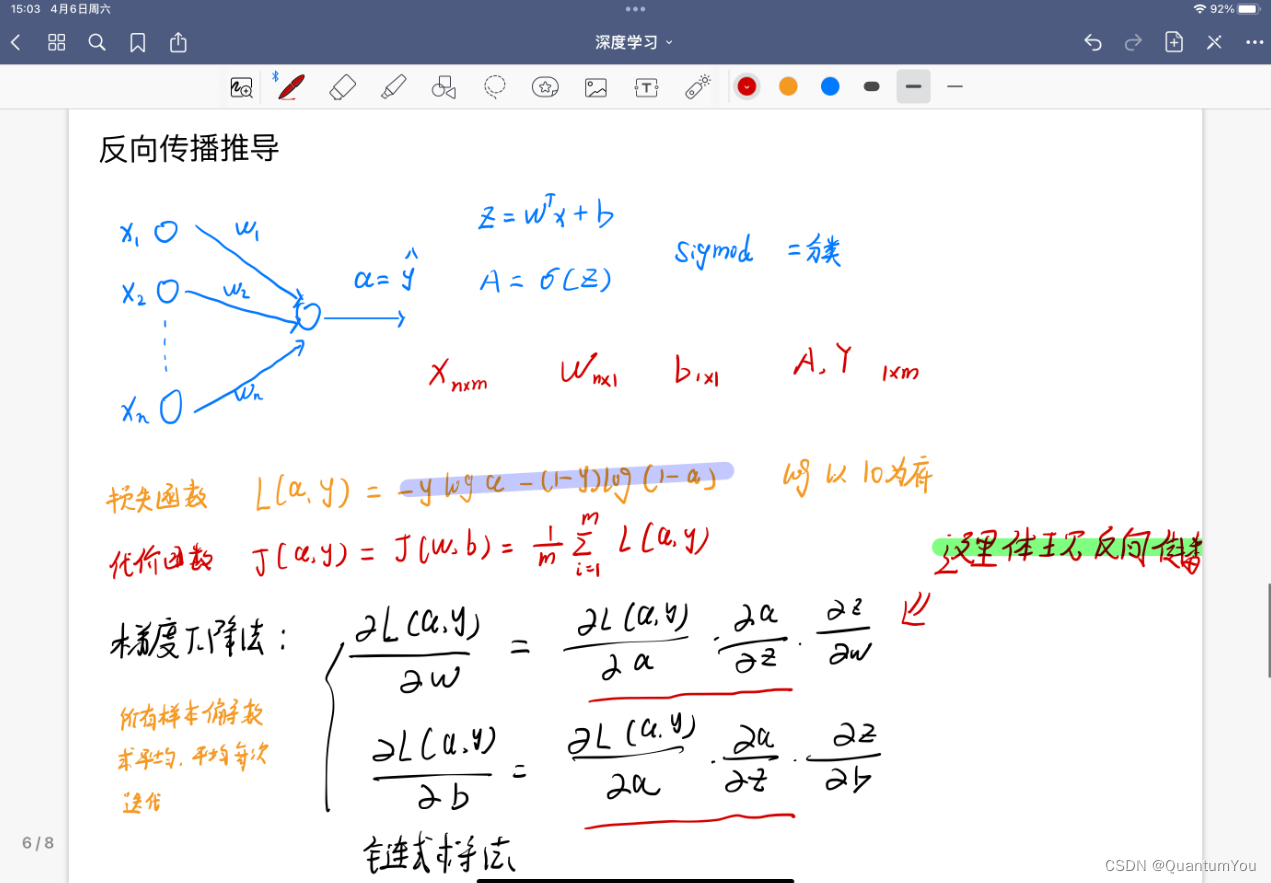
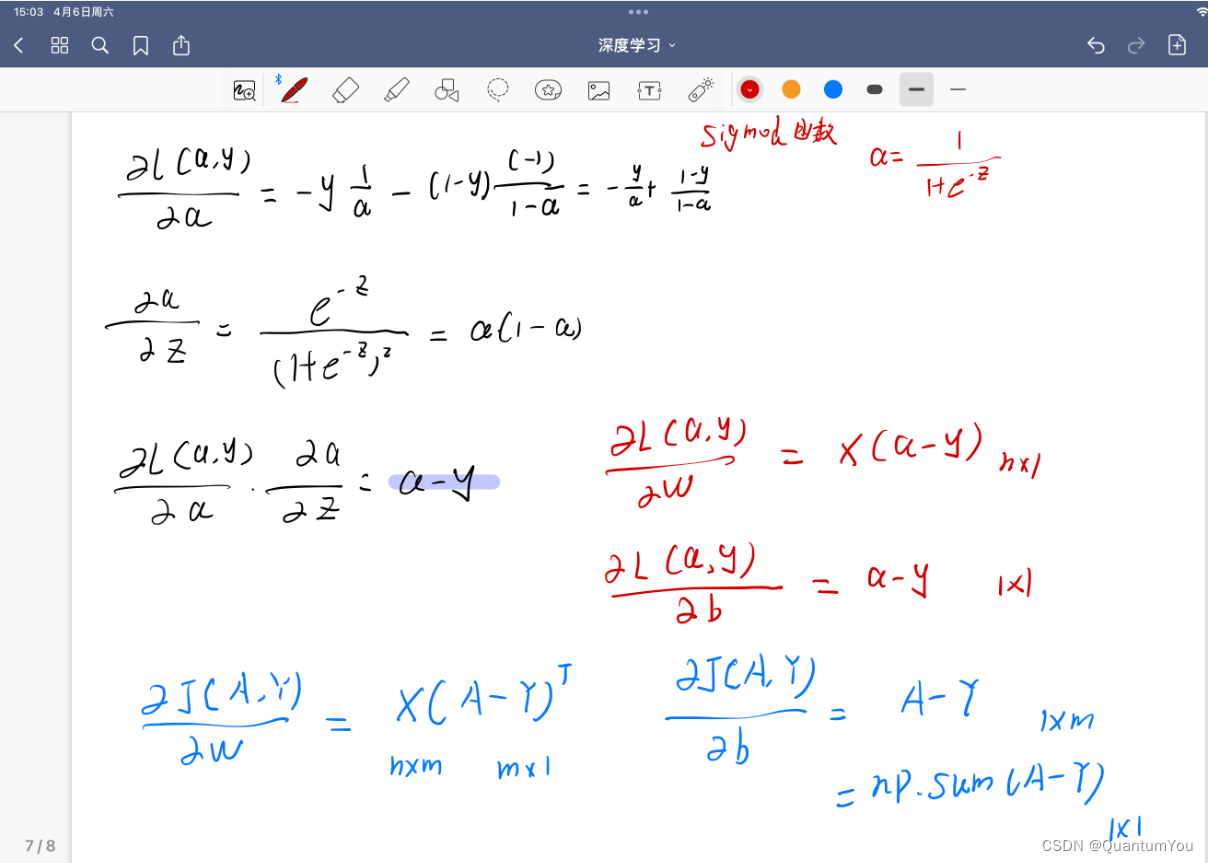
print(train_data_sta[:9,:9])(7) 反向传播过程推导
- 本人手写,字丑勿喷😱😂
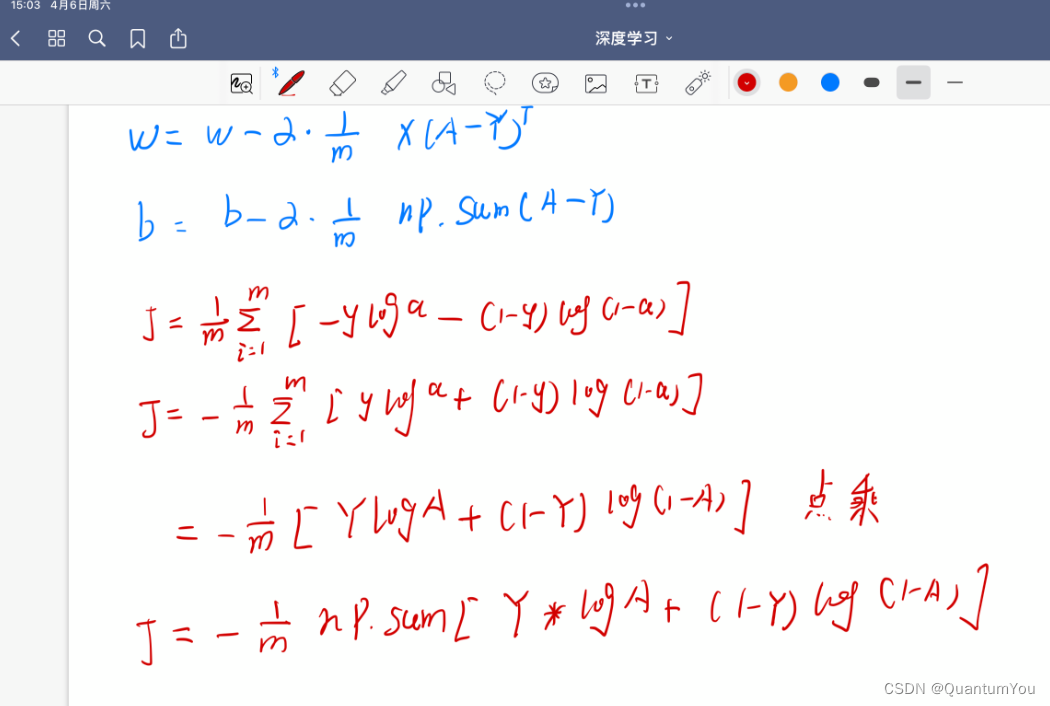
(8)代价函数 梯度下降实现

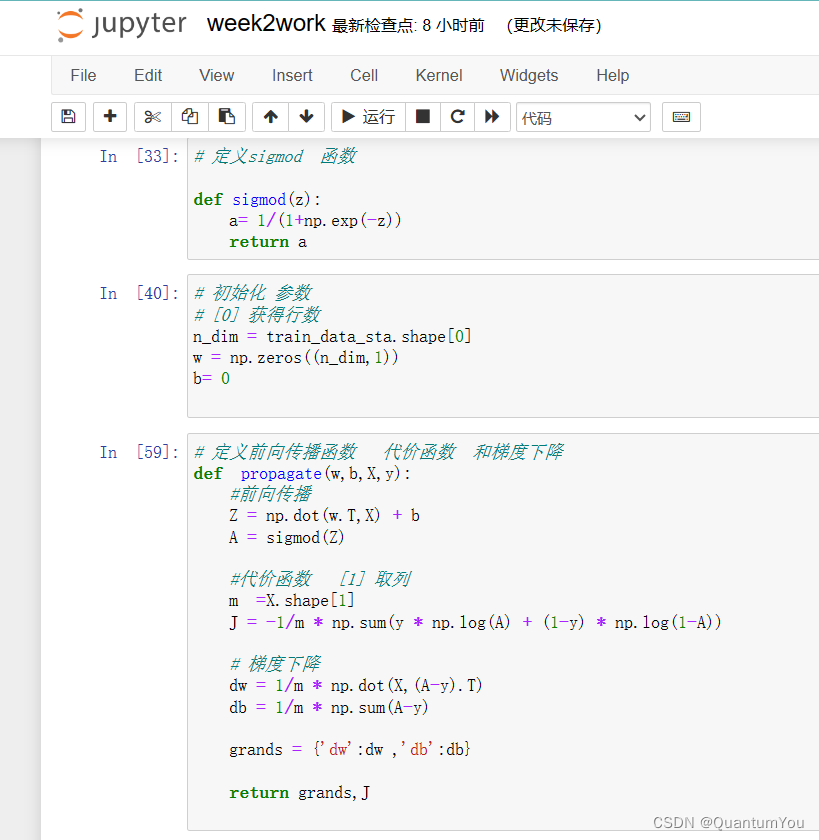
- 定义sigmod 函数 初始化参数
# 定义sigmod 函数 def sigmod(z):a= 1/(1+np.exp(-z))return a
# 初始化 参数
# [0] 获得行数
n_dim = train_data_sta.shape[0]
w = np.zeros((n_dim,1))
b= 0 - 定义前向传播函数 代价函数 和梯度下降
# 定义前向传播函数 代价函数 和梯度下降
def propagate(w,b,X,y):#前向传播 Z = np.dot(w.T,X) + bA = sigmod(Z)#代价函数 [1] 取列m =X.shape[1]J = -1/m * np.sum(y * np.log(A) + (1-y) * np.log(1-A))# 梯度下降dw = 1/m * np.dot(X,(A-y).T)db = 1/m * np.sum(A-y)grands = {'dw':dw ,'db':db}return grands,J
- 优化 与 预测
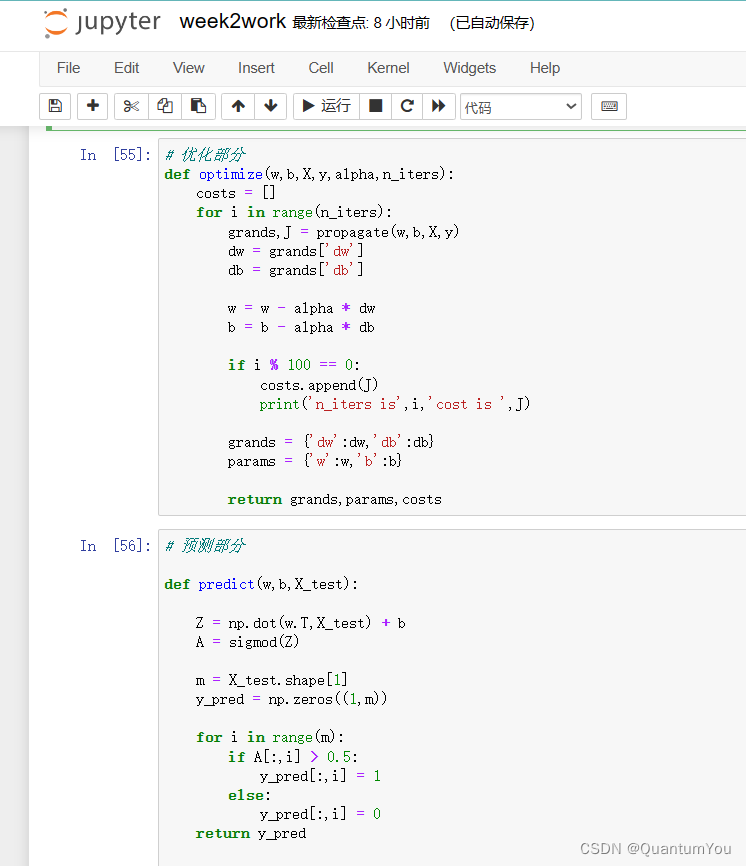
# 优化部分
def optimize(w,b,X,y,alpha,n_iters):costs = [] for i in range(n_iters):grands,J = propagate(w,b,X,y)dw = grands['dw']db = grands['db']w = w - alpha * dw b = b - alpha * dbif i % 100 == 0:costs.append(J)print('n_iters is',i,'cost is ',J)grands = {'dw':dw,'db':db}params = {'w':w,'b':b}return grands,params,costs
# 预测部分def predict(w,b,X_test):Z = np.dot(w.T,X_test) + bA = sigmod(Z)m = X_test.shape[1]y_pred = np.zeros((1,m))for i in range(m):if A[:,i] > 0.5:y_pred[:,i] = 1 else:y_pred[:,i] = 0 return y_pred 预测准确率

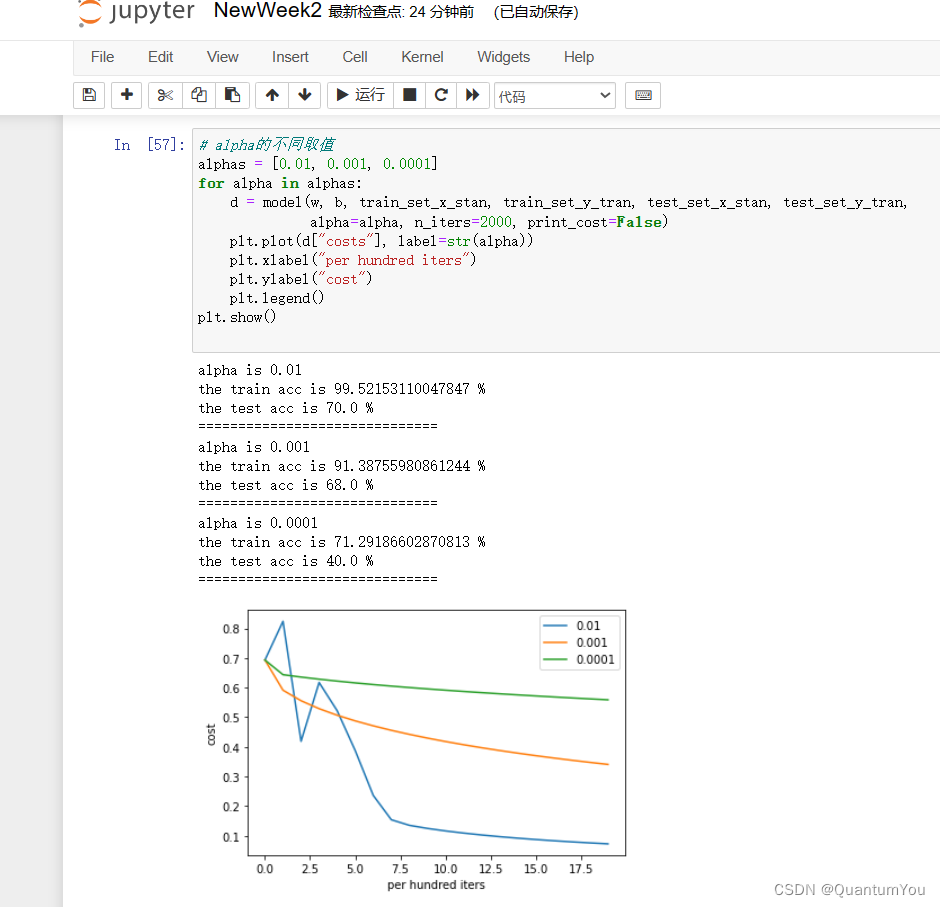
(9)预测图片 完结🌹🌹
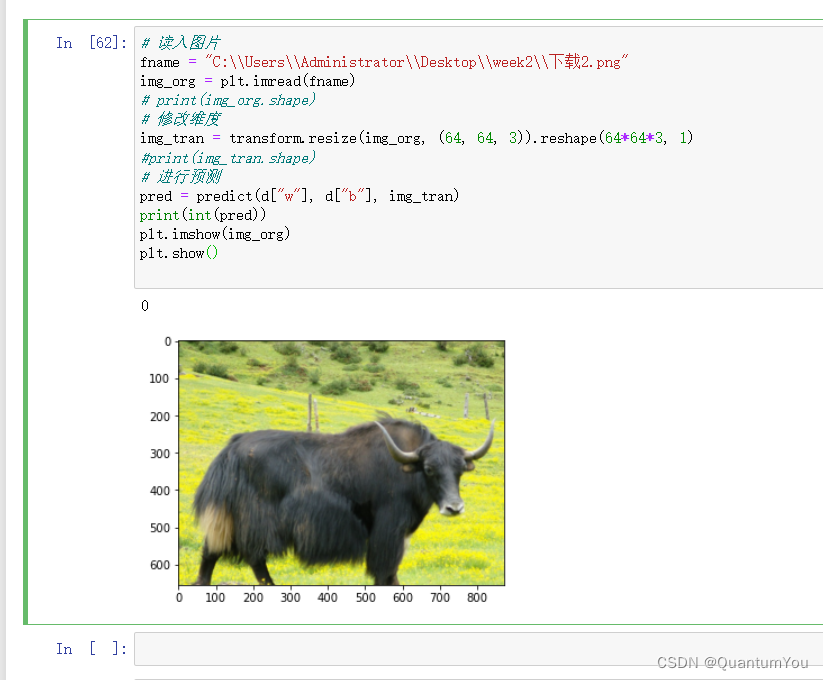
(10)大作业实现总结
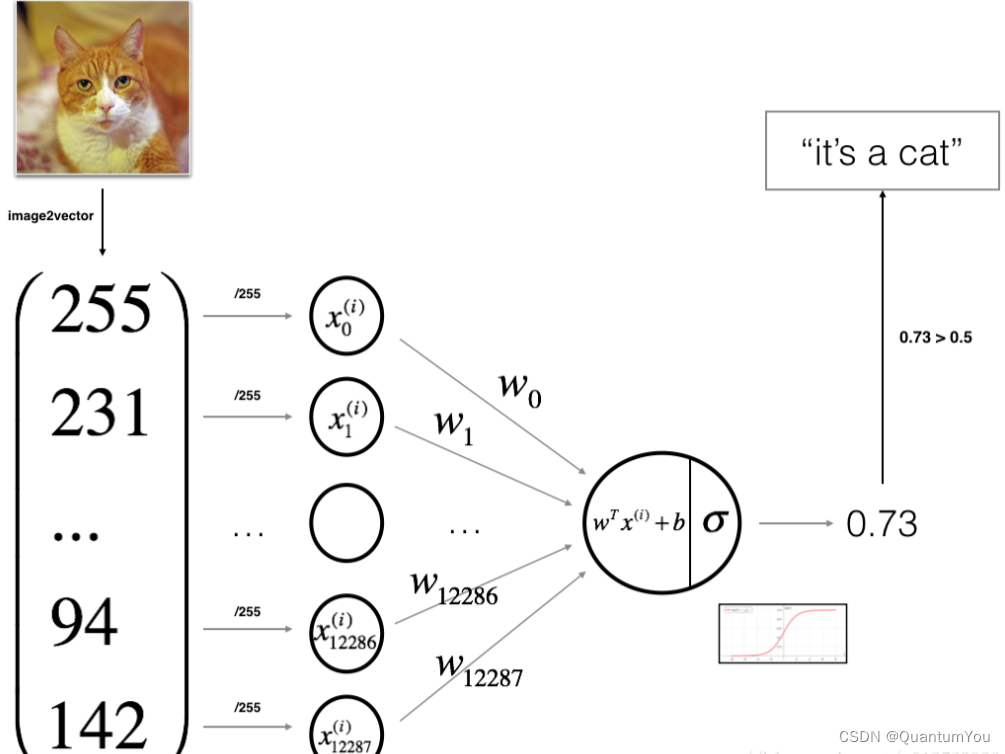
在整个过程中,要搞清楚这里面每一步做的都是为了什么,以及参数w和b在循环:计算当前损失(正向传播)–>计算当前梯度(反向传播)–>更新参数(梯度下降)中是如何求得的,这是比较关键的,还有一个是一定要计算好数据的维度,到哪一步得到的数据应该是什么维度。
- ①建立神经网络的主要步骤是:
定义模型结构(例如输入特征的数量)
初始化模型的参数
循环:
3.1 计算当前损失(正向传播)
3.2 计算当前梯度(反向传播)
3.3 更新参数(梯度下降)
-
②propagate 函数
实现前向和后向传播的成本函数及其梯度。
参数:
w- 权重,大小不等的数组(num_px * num_px * 3,1)
b- 偏差,一个标量
X- 矩阵类型为(num_px * num_px * 3,训练数量)
Y- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)返回:
cost- 逻辑回归的负对数似然成本
dw- 相对于w的损失梯度,因此与w相同的形状
db- 相对于b的损失梯度,因此与b的形状相同 -
③ optimize函数
此函数通过运行梯度下降算法来优化w和b参数:
w- 权重,大小不等的数组(num_px * num_px * 3,1)
b- 偏差,一个标量
X- 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y- 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations- 优化循环的迭代次数
learning_rate- 梯度下降更新规则的学习率
print_cost- 每100步打印一次损失值返回:
params- 包含权重w和偏差b的字典
grads- 包含权重和偏差相对于成本函数的梯度的字典
成本- 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示: 我们需要写下两个步骤并遍历它们:1)计算当前参数的成本和梯度,使用propagate()。2)使用w和b的梯度下降法则更新参数。 使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
-
④predict函数
参数:
w- 权重,大小不等的数组(num_px * num_px * 3,1)
b- 偏差,一个标量
X- 维度为(num_px * num_px * 3,训练数据的数量)的数据返回:
Y_prediction- 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1, -
⑤model函数
参数:
w- 权重,大小不等的数组(num_px * num_px * 3,1)
b- 偏差,一个标量
X- 维度为(num_px * num_px * 3,训练数据的数量)的数据返回:
Y_prediction- 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集num_iterations- 表示用于优化参数的迭代次数的超参数learning_rate- 表示optimize()更新规则中使用的学习速率的超参数print_cost- 设置为true以每100次迭代打印成本
返回:d- 包含有关模型信息的字典。







)
机器学习-机器学习建模步骤/kaggle房价回归实战】)









【MySQL版本】)
