竞争与冒险
进行理想的组合逻辑电路分析与设计时，没有考虑逻辑门的延迟时间（原因）对电路产生的影响，且认为电路的输入和输出均处于稳定的逻辑电平。
实际上，信号经过逻辑门需要一定的时间。不同路径上门电路数目不同，导致信号传输时间不同；或虽然门电路数量相同，但各个门延迟时间有差异。
因此，电路在信号电平变化瞬间，可能与稳态下的逻辑功能不一致，产生错误输出。这种现象就是竞争-冒险现象。
竞争：输入端的变化电平经过一定的路径，到达某一汇合点有先有后，这种现象称为竞争。
冒险：因为竞争而可能出现干扰脉冲的现象称为冒险。（因此竞争不一定冒险）
判断是否具有竞争-冒险
代数法
在逻辑函数表达式中，若某个变量同时以原变量和反变量两种形式出现， 就具备了竞争条件。
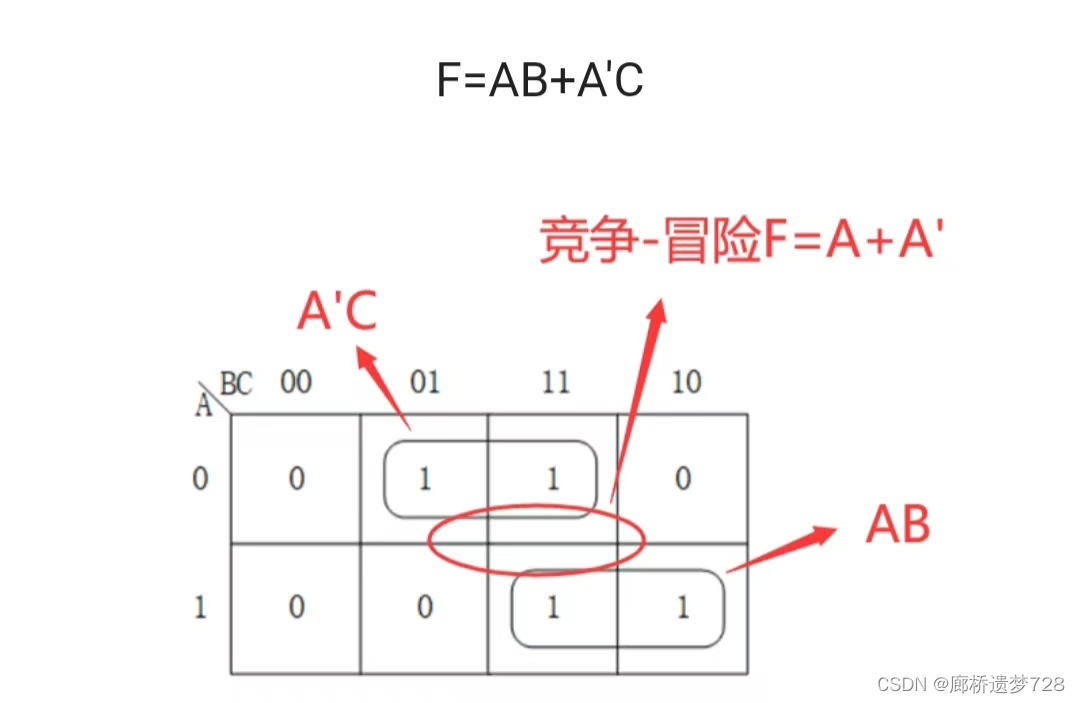
去掉其余变量（也就是将其余变量取固定值 0 或 1），留下有竞争能力的变量，如果表达式为 F=A+A'，就会产生 0 型冒险（F应该为1而实际却为0）；如果表达式为 F=AA'，就会产生 1 型冒险。
卡诺图法
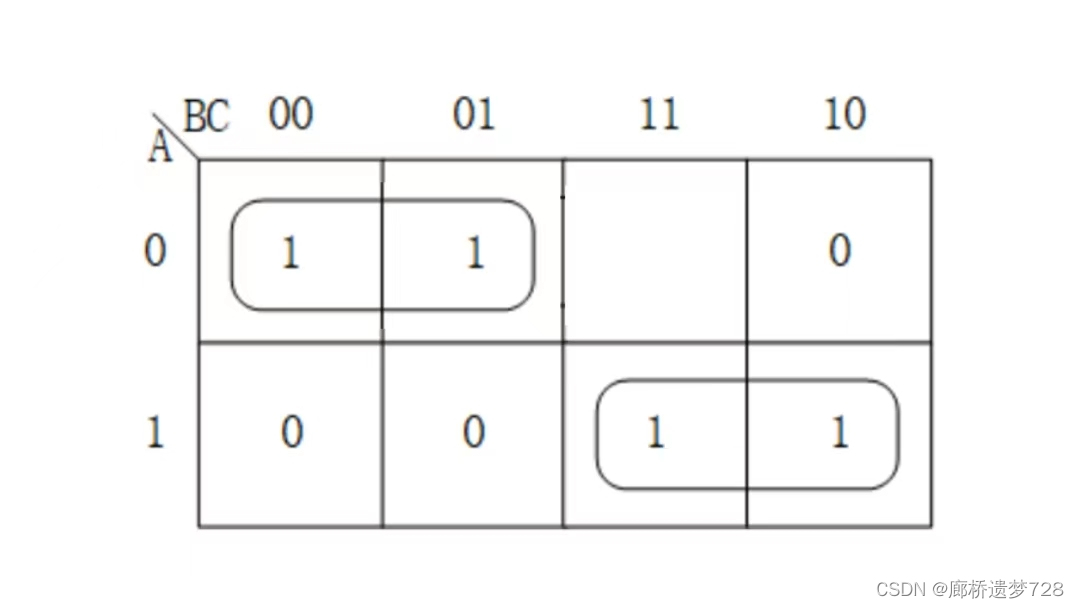
观察卡诺图中是否有两个圈相切但不相交的情况，如有则存在竞争-冒险的现象
对于上图情况就存在竞争-冒险现象。而以下情况就没有冒险现象。
观察法
根据电路图，观察输入变量到达输出端的多个路径上经过的门电路器件的数量是否不同，如果不同，则有可能出现竞争-冒险现象。
实验法
实际上逻辑电路级数多、输入变量多，判断竞争冒险非常复杂，广泛采用仿真和实际测量逻辑电路来观察是否存在竞争冒险的现象。
消除竞争与冒险
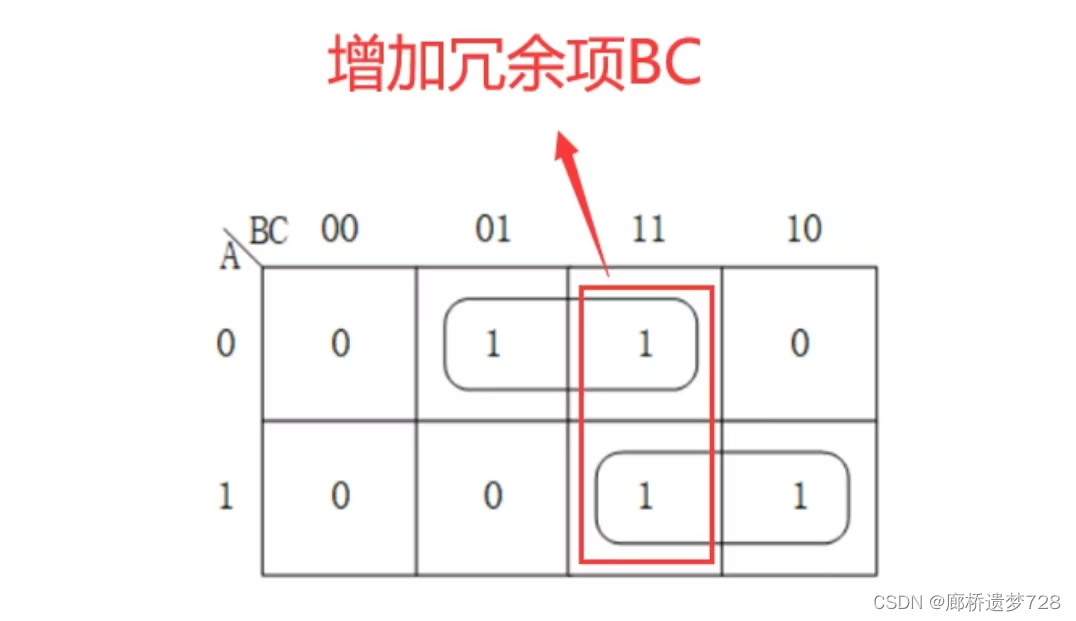
增加冗余项
适当的逻辑表达式中增加一些冗余项，它们的增加不改变逻辑功能，但是可以消除互补信号产生的竞争-冒险现象。
方法：在相切处多画一个卡诺圈，将切点给覆盖掉。
例如：
得到F=AB+A'C+BC，多了BC并不影响结果，此时当B=C=1时，F=A+A'+1=1。这意味这不管B、C怎么变，F恒为1，这样竞争-冒险就消失了。
消去互补项
例如，函数式，在B=C=0时，
，则有可能出现冒险。将该式子变换为
，此时将互补项AA'消去，不会出现竞争-冒险。
接入滤波电容
尖峰脉冲一般都很窄，输出端并接一个很小的滤波电容（几十皮法），足以将其幅度削弱到门电路的阈值电压以下。
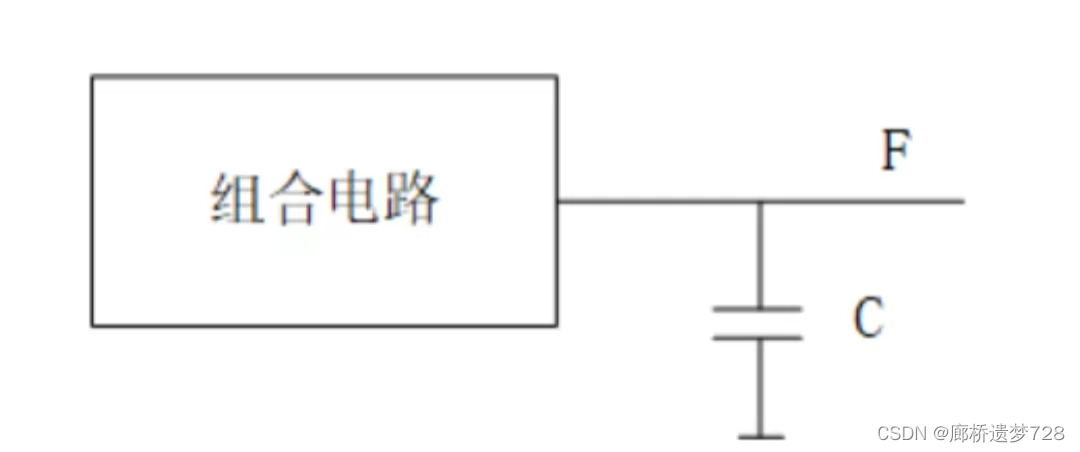
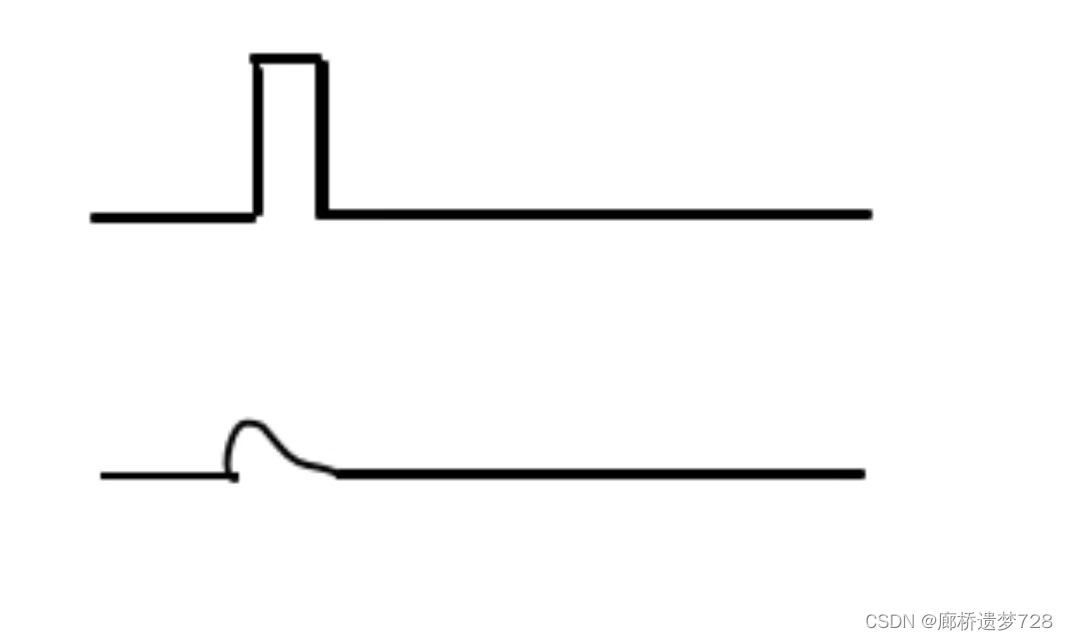
电容两端的电压不会发生突变，当电压上升的时候，实际上是对电容的充电的过程，由于尖峰脉冲非常窄，所以刚充电一点就会立刻放电，从而达到削弱脉冲的效果。
