静电场概述

什么是静电场

静电场是由特殊的电荷引起场。

这个特殊的电荷指：相对于观察者静止、且电量不随时间改变的电荷。

库仑定律

指在无限大的真空中，当两个静止的小带电体之间的距离远远大于本身的几何尺寸时，该两带电体之间的作用力。

如图所示：

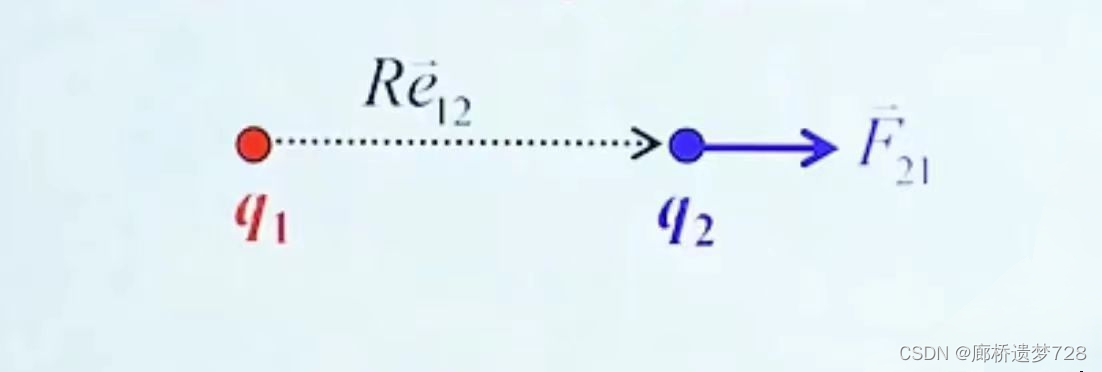
点电荷q1作用于点电荷q2的作用力为：

$\vec{F}_{21}=\frac{q_{1}q_{2}}{4\pi \varepsilon _{o}}\frac{\vec{e_{12}}}{R^{2}}$

式中：ε为真空的介电常数，其值约为1/36π×10^(-9)F/m。

库仑定律只能直接用于点电荷。

所谓点电荷，是指当带电体尺度远小于它们之间的距离时，将其电荷集中于一点的理想化模型。

问题：q1和q2相隔了一定的距离，为什么还会有相互作用力？

电荷q1对电荷q2的作用力，是由于q1在空间产生电场，电荷q2在电场中受力。我们用电场强度来描述电场。

电荷密度

在介绍电场强度之前，先来看看电荷密度。

对于实际的带电体，一般分布在一定区域内，我们称其为：分布电荷。通常用电荷体密度来描述电荷的空间分布情况：

$\rho =\lim_{\bigtriangleup V \to 0}\frac{\bigtriangleup q}{\bigtriangleup V}=\frac{dq}{dV}$

如果电荷分布在宏观尺度h很小的薄层内，则可认为电荷分布在一个几何曲面上，用面密度来描述其分布：

$\rho_{s} =\lim_{\bigtriangleup S \to 0}\frac{\bigtriangleup q}{\bigtriangleup S}=\frac{dq}{dS}$

对于一条细线上的电荷用线密度来描述：

$\rho _{l}=\lim_{\bigtriangleup l \to 0}\frac{\bigtriangleup q}{\bigtriangleup l}=\frac{dq}{dl}$

电场强度

定义：空间一点的电场强度为该点的单位正试验电荷所收到的力：

$\vec{E}=\frac{\vec{F}}{q}$

可以看出电场强度是空间坐标的矢量函数。

单位正试验电荷：体积小、带电量小、引入电场后不影响电场分布的电荷。

1.点电荷在真空中电场强度

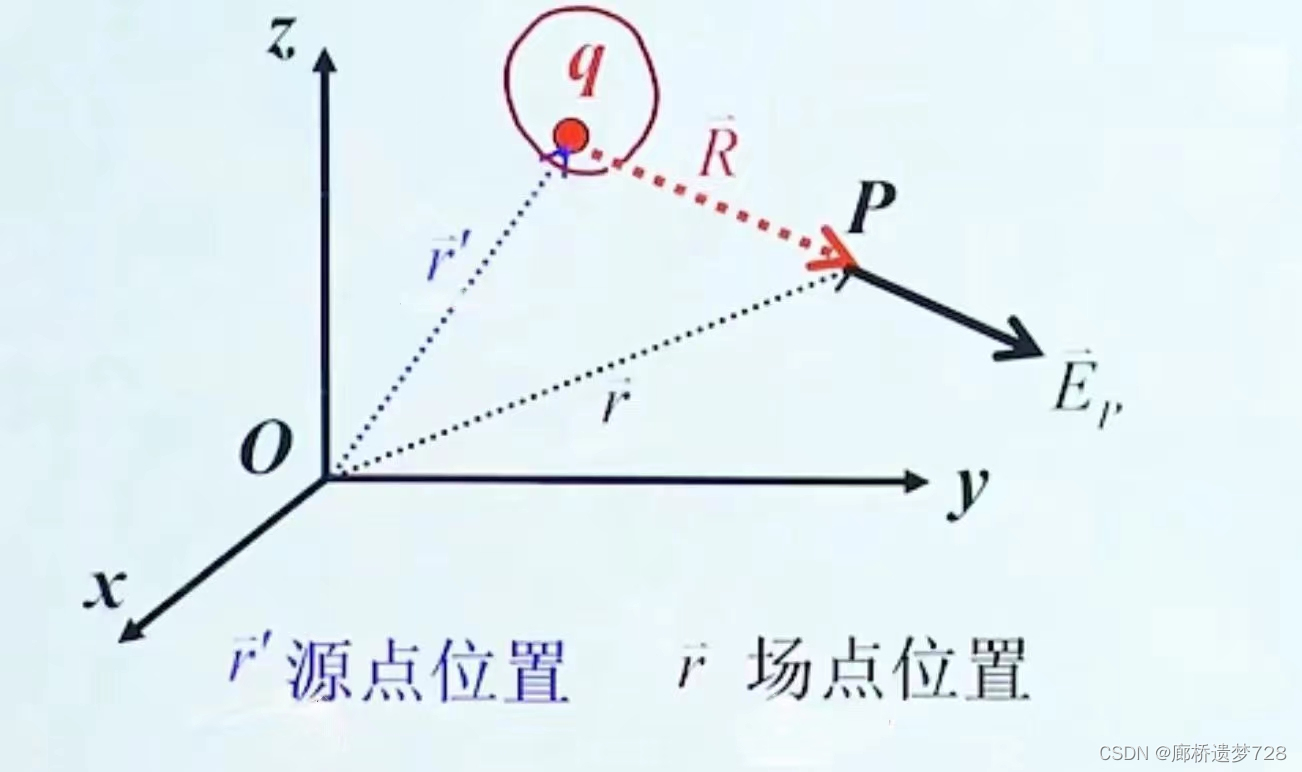
$\vec{E_{P}}=\frac{q}{4\pi \varepsilon _{o}}\frac{\vec{e_{R}}}{R^{2}}=\frac{q}{4\pi \varepsilon _{o}}\frac{\vec{r}-\vec{r}{}'}{\left | \vec{r}-\vec{r}{}' \right |^{3}}$

若有n个点电荷，则产生的电场强度为：

$\vec{E_{P}}=\sum_{i=1}^{n}\frac{q_{i}}{4\pi \varepsilon _{o}}\frac{\vec{r}-\vec{r_{i}}{}'}{\left | \vec{r}-\vec{r_{i}}{}' \right |^{3}}$

2.连续分布电荷的电场强度

体分布电荷产生的电场强度：

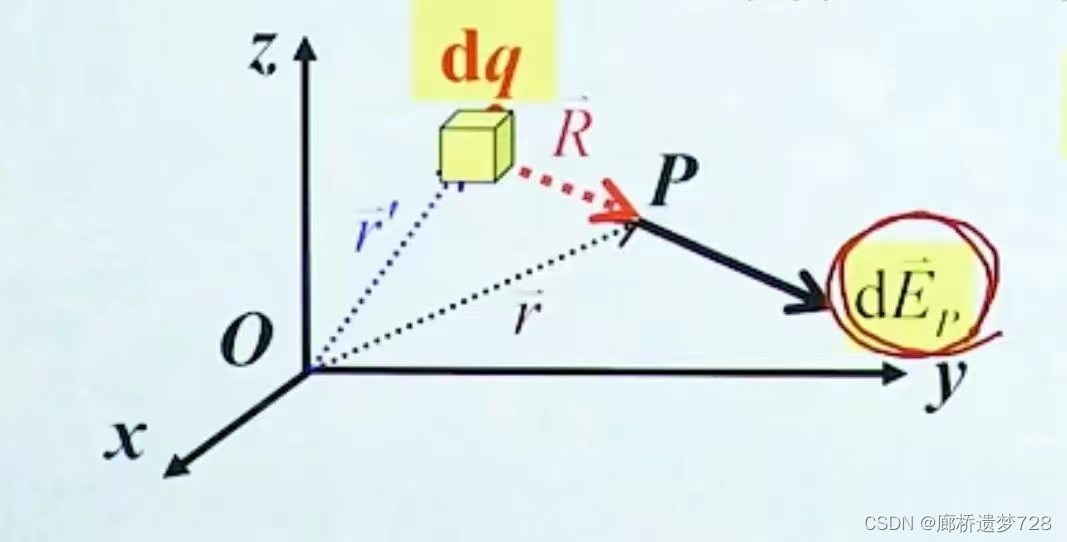
$d\vec{E}_{p}=\frac{dq}{4\pi \varepsilon _{o}}\frac{\vec{e_{R}}}{R^{2}}$

$\vec{E}_{P}=\int dE_{P}=\frac{1}{4\pi \varepsilon _{o}}\int \frac{\vec{e_{R}}dq}{R^{2}}$

得：

$\vec{E}(r)=\frac{1}{4\pi \varepsilon _{o}}\int _{V}\frac{\rho (r{}')(\vec{r}-\vec{r}{}')}{\left | \vec{r}-\vec{r}{}' \right |^{3}}dV{}'$

面分布电荷：

$\vec{E}(r)=\frac{1}{4\pi \varepsilon _{o}}\int _{S}\frac{\rho _{s}(r{}')(\vec{r}-\vec{r}{}')}{\left | \vec{r}-\vec{r}{}' \right |^{3}}dS{}'$

线分布电荷：

$\vec{E}(r)=\frac{1}{4\pi \varepsilon _{o}}\int _{l}\frac{\rho _{l}(r{}')(\vec{r}-\vec{r}{}')}{\left | \vec{r}-\vec{r}{}' \right |^{3}}dl{}'$

静电场的电位

1.环路定理

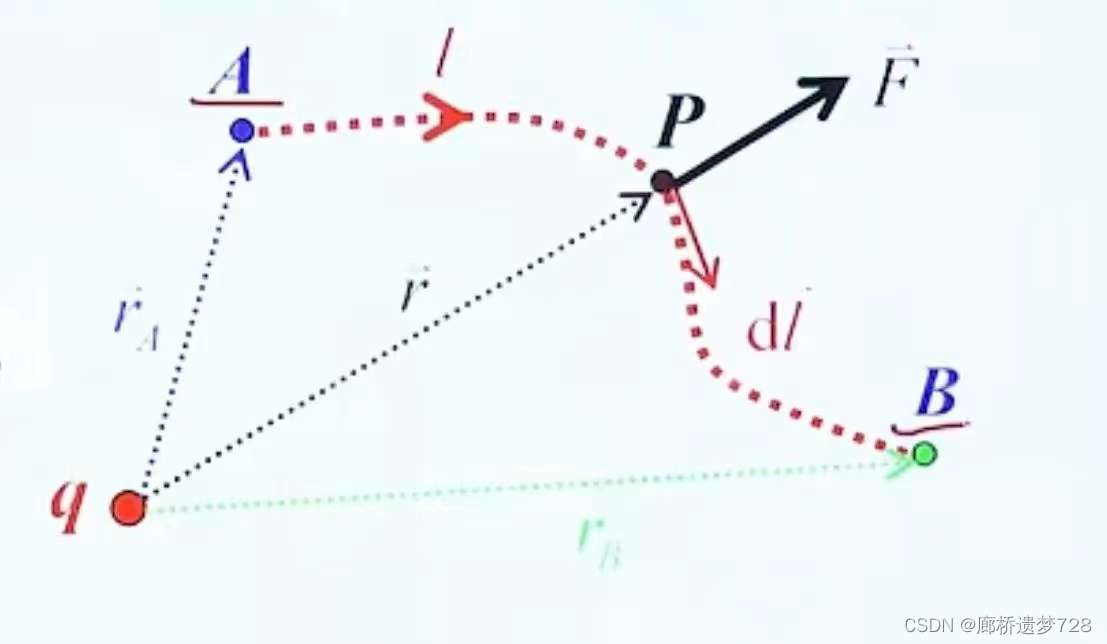
将实验电荷qt沿路径l从A到B，电场力做功为：

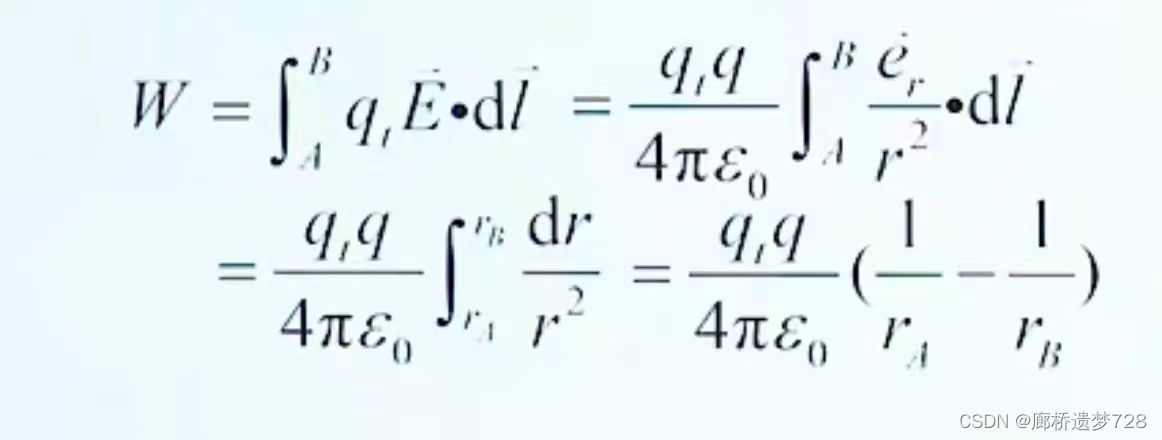
由上述公式可知：

a、发现电场力做功只与起点A和终点B有关，与路径无关。(也适用于多个电荷产生的电场)

b、在静电场中，沿闭合路径移动电荷一圈，电场力做功为0。即：

$\oint _{l}\vec{E}\cdot d\vec{l}=0$

上式为环路定理(积分形式)，说明静电场是一个守恒场(保守场)。

由斯托克斯公式可得：

$\oint _{l}\vec{E}\cdot d\vec{l}=\int _{S}(\bigtriangledown \times \vec{E})\cdot d\vec{S}=0$

故 $\bigtriangledown \times \vec{E}=0$ (环路定理的微分形式)，说明在静电场中，电场强度的旋度处处为0，静电场为无旋场。

2.静电场电位

由 $\bigtriangledown \times (\bigtriangledown \varphi )\equiv 0$ 将E变成 $\vec{E}=\bigtriangledown \varphi$ 的形式。

而▽φ为变化率增加最快(梯度)，E为电位下降最快，故需要添加负号“ - ”，即：

$\vec{E}=-\bigtriangledown \varphi$

我们将φ定义为电位。

将之前电场力做功的公式进行一些数学变化：

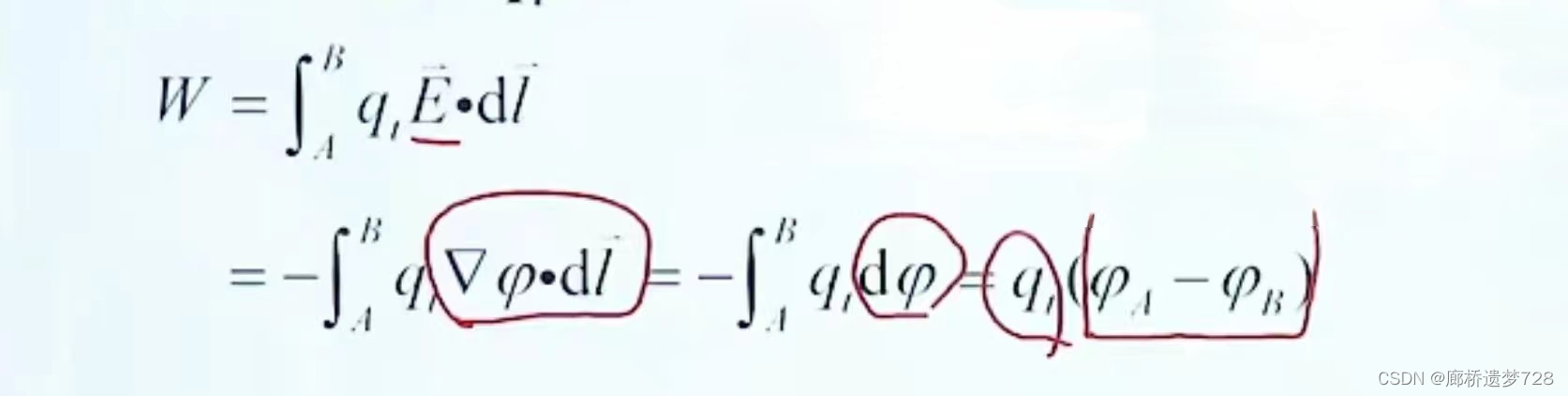
当qt=1时：

$\varphi _{A}-\varphi _{B}=\int_{A}^{B}\vec{E}\cdot d\vec{l}= U_{AB}$

可以得出以下结论：

a、两点之间的电位差有确定的数值，与路径无关。

b、AB之间的电压，等于移动单位正电荷从A点到B点电场力所做功。

参考点

由

$\bigtriangledown (\varphi +C)=\bigtriangledown \varphi +\bigtriangledown C=\bigtriangledown \varphi =-\vec{E}$

可知，同样的电场强度E可对应许多不同的电位φ。故：电位φ的值是相对的，而选择参考点后(规定其电位为0)，电位就能唯一确定。当电荷分布在有限区域时，通常选取无穷远处为参考点。

当选取无穷远处为参考点后，各种电荷产生的电位如下：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/800766.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！