import copy
import random
import matplotlib
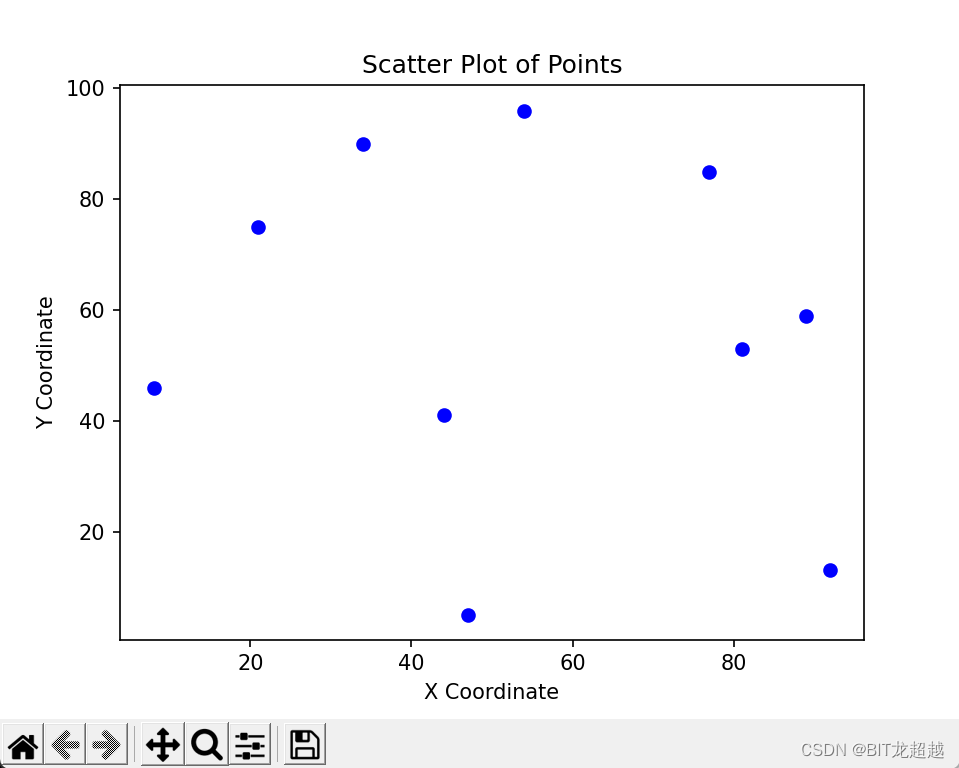
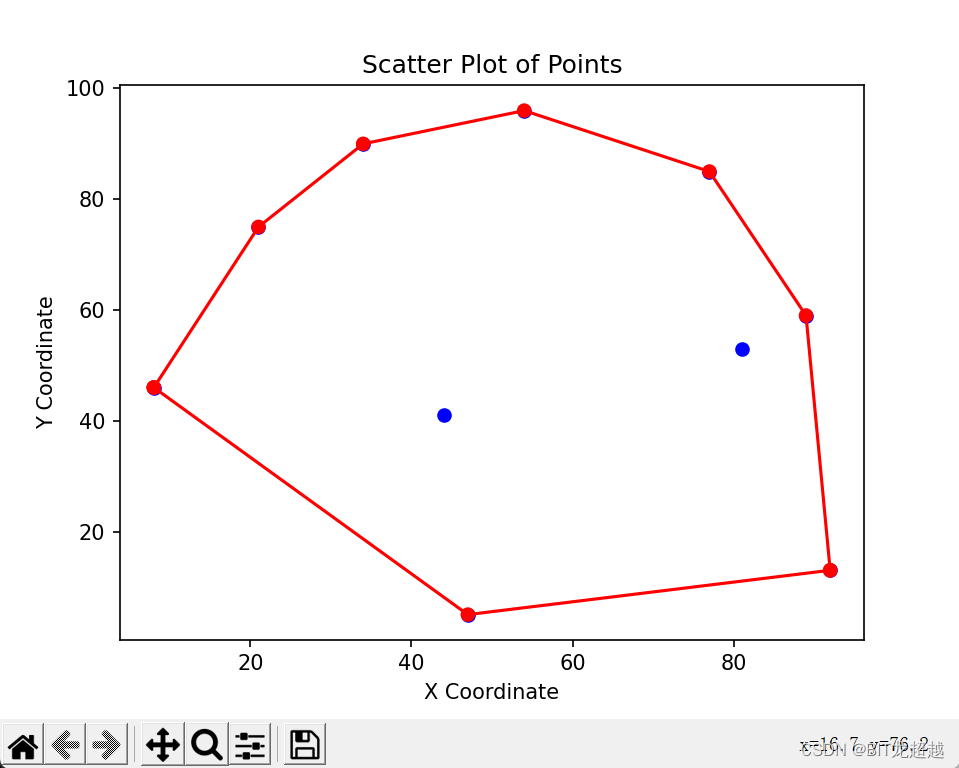
import mathdef distance_p2l(point, line_point1, line_point2):if (line_point2[0] - line_point1[0]) == 0:return abs(point[0] - line_point2[0])# 计算直线的斜率m = (line_point2[1] - line_point1[1]) / (line_point2[0] - line_point1[0])# 计算直线的截距b = line_point1[1] - m * line_point1[0]# 计算距离d = abs(m * point[0] - point[1] + b) / math.sqrt(m ** 2 + 1)return ddef node_above_line(node, line0, line1,upper_convex=True,left_convex=True):real_y = node[1]# y_on_line =(node[0]-line0[0])/(line1[0]-line0[0])*(line1[1]-line0[1])+line0[1]if (line1[0] - line0[0])!=0:print(node[1],node[0] - line0[0] / (line1[0] - line0[0]) * (line1[1] - line0[1]) + line0[1])if node[1] > (node[0]-line0[0])/(line1[0]-line0[0])* (line1[1]-line0[1])+line0[1]:return Trueelse:return Falseelse:if node[0]<line0[0]:if upper_convex==True:if left_convex:return Trueelse:return Falseif upper_convex==False:if left_convex:return Falseelse:return Trueelse:if upper_convex == True:if left_convex:return Falseelse:return Trueif upper_convex==False:if left_convex:return Trueelse:return Falsedef cal_convex_hull_point(min_x_node, max_x_node, upper_set,upper_convex=True):if len(upper_set) == 0:return [min_x_node, max_x_node]upper_set_distance2line = [distance_p2l(point, max_x_node, min_x_node) for point in upper_set]max_idx = upper_set_distance2line.index(max(upper_set_distance2line))farthest_p = upper_set[max_idx]upper_set_mins =  [node for node in upper_set if node != farthest_p]left_subset_of_upper, right_subset_of_upper = [], []for node in upper_set_mins:if node_above_line(node, farthest_p, min_x_node,upper_convex=upper_convex,left_convex=True)==upper_convex:left_subset_of_upper.append(node)if node_above_line(node, farthest_p, max_x_node,upper_convex=upper_convex,left_convex=False)==upper_convex:right_subset_of_upper.append(node)lu = cal_convex_hull_point(min_x_node,farthest_p,left_subset_of_upper,upper_convex)ru = cal_convex_hull_point(farthest_p,max_x_node,right_subset_of_upper,upper_convex)return lu+rudef divide_conquer(nodes):sorted_nodes = sorted(nodes, key=lambda x: x[0])max_x_node = sorted_nodes[-1]min_x_node = sorted_nodes[0]upper_set = []lower_set = []lu,ru,ll,rl = [],[],[],[]for node in sorted_nodes[1:-1]:if node_above_line(node, max_x_node, min_x_node):upper_set.append(node)else:lower_set.append(node)if len(upper_set)!=0:upper_set_distance2line = [distance_p2l(point, max_x_node, min_x_node) for point in upper_set]max_idx = upper_set_distance2line.index(max(upper_set_distance2line))farthest_p = upper_set[max_idx]upper_set_mins = [node for node in upper_set if node != farthest_p]left_subset_of_upper, right_subset_of_upper = [], []for node in upper_set_mins:if node_above_line(node, farthest_p, min_x_node,left_convex=True):left_subset_of_upper.append(node)if node_above_line(node, farthest_p, max_x_node,left_convex=False):right_subset_of_upper.append(node)lu = cal_convex_hull_point(min_x_node, farthest_p, left_subset_of_upper)ru = cal_convex_hull_point(farthest_p, max_x_node, right_subset_of_upper)if len(lower_set) != 0:lower_set_distance2line = [distance_p2l(point, max_x_node, min_x_node) for point in lower_set]max_idx = lower_set_distance2line.index(max(lower_set_distance2line))farthest_p = lower_set[max_idx]lower_set_mins = [node for node in lower_set if node != farthest_p]left_subset_of_lower, right_subset_of_lower = [], []for node in lower_set_mins:if node_above_line(node, farthest_p, min_x_node,upper_convex=False,left_convex=True)==False:left_subset_of_lower.append(node)if node_above_line(node, farthest_p, max_x_node,upper_convex=False,left_convex=False)==False:right_subset_of_lower.append(node)ll = cal_convex_hull_point(min_x_node, farthest_p, left_subset_of_lower,upper_convex=False)rl = cal_convex_hull_point(farthest_p, max_x_node, right_subset_of_lower,upper_convex=False)point_set = list(set(ll + lu + rl + ru))print("set point",point_set)convex0 = lu + ruconvex1 = ll + rlconvex0 = [convex0[i] for i in range(len(convex0)) if i==0 or i>0 and convex0[i]!=convex0[(i-1)]]convex1 = [convex1[i] for i in range(len(convex1)) if i==0 or i>0 and convex1[i] != convex1[i - 1]]convex1 = [convex1[i] for i in range(len(convex1) - 1, -1, -1)]convex  = convex0 +convex1convex = convex + [convex[0]]print("lines are ", convex)return convexdef draw_points(points, convex_p=None):import matplotlib.pyplot as pltplt.ion()# 输入点的坐标# points = [(0, 55), (40, 93), (20, 70), (10, 60)]  # 示例坐标# 分离 x 和 y 坐标x_coords = [point[0] for point in points]y_coords = [point[1] for point in points]# 绘制点plt.scatter(x_coords, y_coords, color='blue')if convex_p != None:c_x = [p[0] for p in convex_p]c_y = [p[1] for p in convex_p]colors = ['red'] * len(c_y)plt.scatter(c_x, c_y, color=colors)plt.plot(c_x, c_y, color='red')# 添加标题和坐标轴标签plt.title('Scatter Plot of Points')plt.xlabel('X Coordinate')plt.ylabel('Y Coordinate')plt.pause(5)plt.ioff()plt.clf()def pnpoly(vertices, testp):n = len(vertices)j = n - 1res = Falsefor i in range(n):if (vertices[i][1] > testp[1]) != (vertices[j][1] > testp[1]) and \testp[0] < (vertices[j][0] - vertices[i][0]) * (testp[1] - vertices[i][1]) / (vertices[j][1] - vertices[i][1]) + vertices[i][0]:res = not resj = ireturn resfor i in range(38,100):print('seed',i)random.seed(i)nodes = [(random.randint(0, 100), random.randint(0, 100)) for i in range(10)]print(nodes)draw_points(nodes)convex_p = divide_conquer(nodes)draw_points(nodes, convex_p)