文章目录
- 前言
- 一、邻接矩阵法(顺序存储)
- 1.无向图存储邻接矩阵算法
- 2.有向图存储邻接矩阵算法
- 二、邻接表法(图的链式存储结构)
- 总结
前言
- 邻接矩阵法(图的顺序存储结构)
1.1 无向图邻接矩阵算法
1.2 有向图邻接矩阵算法 - 邻接表法(图的一种链式存储结构)
一、邻接矩阵法(顺序存储)
- 定义:用一个一维数组存储顶点,一个二维数组存储边的信息(各顶点之间邻接关系),n个顶点是n×n的矩阵,若(vi,vj)属于E ,则A[i][j]=1,否则等于0;对于带权图,则邻接矩阵中对应项存放着该边对应的权值,若顶点vi和vj不相连,则用∞来表示这两个顶点之间不存在边【是表示顶点之间相邻关系的矩阵。所谓两顶点的相邻关系即它们之间有边相连。】
- 注意
①无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储
②邻接矩阵表示法的空间复杂的为O(n^2),其中n为图的定点数|V| - 图的邻接矩阵存储表示法具有以下特点:
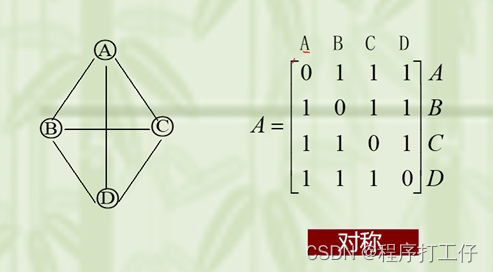
1)无向图的邻接矩阵一定是一个对称矩阵(并且唯一),因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素即可
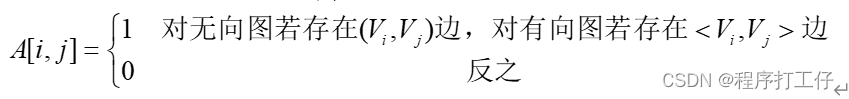
2)对于无向图,邻接矩阵的第i行(或第i列)非零元素(或非无穷元素)的个数正好是第i个顶点的度TD(vi)
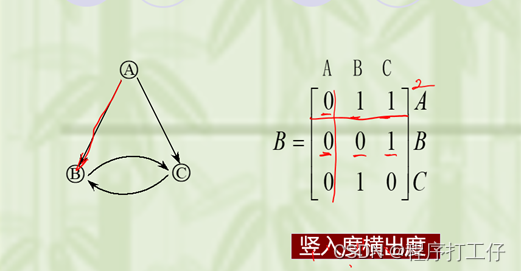
3)对于有向图,邻接矩阵的第i行(或第i列)非零元素(或非无穷元素)的个数正好是第i个顶点的出度OD(vi)(或入度ID(vi)),第i行和第i列和是有向图第i结点的度
(有向图:行出度,竖入度)
4)用邻接矩阵存储图,很容易确定图中任意两个顶点时间是否有边相连。但是,要确定图中有多少边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。这是用邻接矩阵存储图的局限性
5)稠密图适合使用邻接矩阵的存储表示
- 无向图的邻接矩阵是对称的,如果A[i,j]=1,必有A[j,i]=1。这说明,只输入和存储其上三角阵元素即可得到整个邻接矩阵。
- 一般有向图的邻接矩阵是不对称的,A[i,j]不一定等于A[j,i]。
- 邻接矩阵用二维数组即可存储,定义如下:
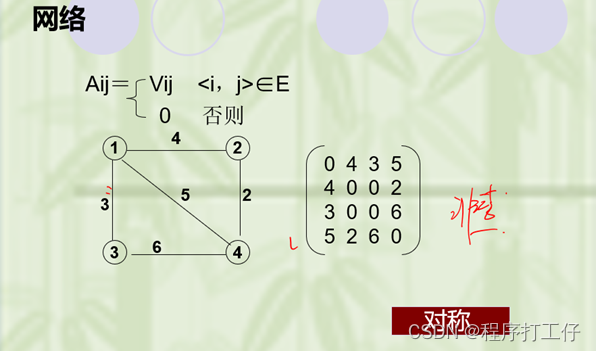
int adjmatrix = ARRAY[n][n]; - 如果图的各边是带权的,只需将矩阵中的各个1元素换成相应边的权即可。
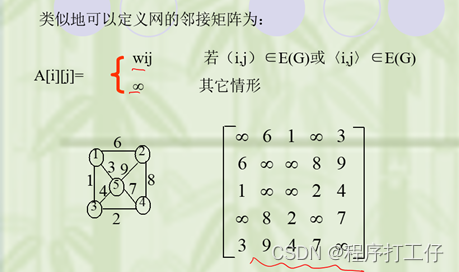
- 对于无向图而言:顶点Vi的度是邻接矩阵中第i行(或列)的元素之和。
- 对于有向图而言:
顶点Vi的出度是邻接矩阵中第i行的元素之和。
顶点Vi的入度是邻接矩阵中第i列的元素之和
1.无向图存储邻接矩阵算法
int creatgraph (int adjarray[ ][ ])
{int i,j,v1,v2,num;scanf (“%d”,&num); /*输入顶点数*/if (num>0){for (i=1;i<=num;i++)for (j=1;j<=num;j++)adjarry [i][j]=0; /*矩阵初始化*/
do{scanf (“%d,%d”,&v1,&v2); /*输入边*/adjarray[v1][v2]=1;adjarray[v2][v1]=1;} while(v1!=0 && v2!=0);}else num=0;return num;}2.有向图存储邻接矩阵算法
int creatgraph (int adjarray[ ][ ])
{int i,j,v1,v2,num;scanf (“%d”,&num); /*输入顶点数*/if (num>0){for (i=1;i<=num;i++)for (j=1;j<=num;j++)adjarry [i][j]=0; /*矩阵初始化*/
do{scanf (“%d,%d”,&v1,&v2); /*输入边*/adjarray[v1][v2]=1;} while(v1!=0 && v2!=0);}else num=0;return num;}二、邻接表法(图的链式存储结构)
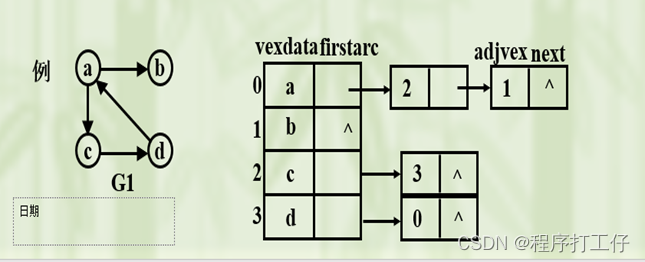
1.定义:对图G中每个顶点建立一个单链表,第i个单链表结点表示依附于顶点vi的边(有向图是以顶点vi为尾的弧)
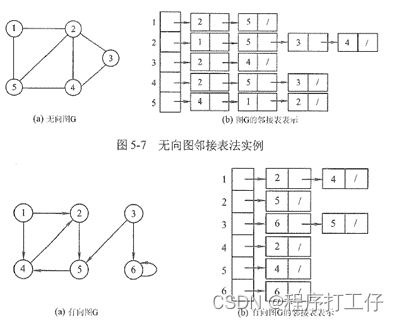
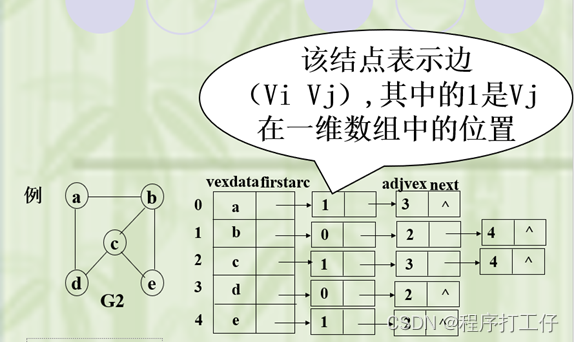
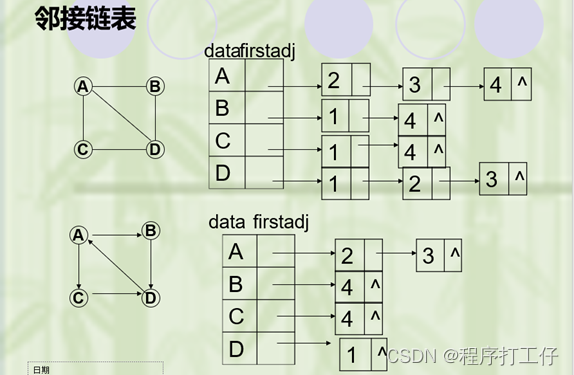
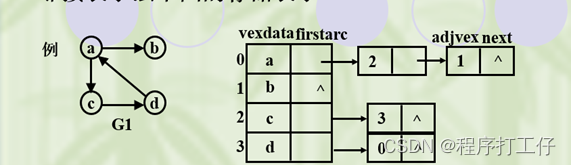
2. 邻接表特点
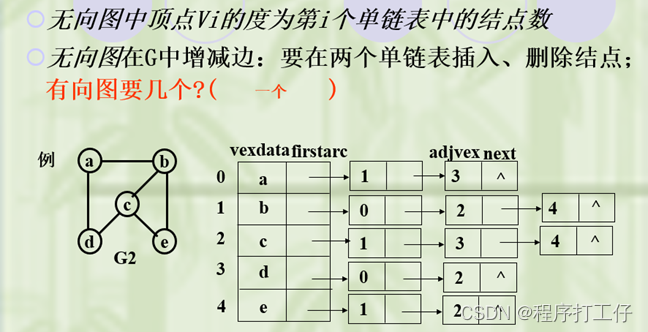
(1)如果G为无向图,则所需存数空间为O(|V|+2|E|),若为有向图,则需O(|V+|E|)
(2)邻接表中给定一顶点,能够很容易找到所有邻边,而邻接矩阵中需要扫描一行,时间为O(n);但是若要确定两个顶点间是否存在边,则在邻接矩阵里可以立即查找,而在邻接表需要对相应结点的边表里查找另一结点,效率较低
(3)有向图邻接表中,求一个给定顶点的出度只需计算其邻接表结点个数,但要求入度,需遍历整表,也可用逆邻接表
(4)无向图设存储顶点的一维数组大小为m(m>=图的顶点数n),
图的边数为e,G占用存储空间为:m+2*e。(有向图)G占用存储空间与G的顶点数、边数均有关;适用于边稀疏的图
(5)有向图中
顶点Vi的出度为第i个单链表中的结点个数
顶点Vi的入度为整个单链表中邻接点域值是i的结点个数
判定两顶点v,u是否邻接:要看v对应线性链表中有无对应的结点u
总结
- 邻接矩阵法(图的顺序存储结构)
1.1 无向图邻接矩阵算法
1.2 有向图邻接矩阵算法 - 邻接表法(图的一种链式存储结构)




--- 前端开发语言之HTML、CSS、JavaScript)





 更新日志)








