一.实验目的
- 掌握图的连通性。
- 掌握并查集的基本原理和应用。
二.实验步骤与结果
1.定义
(1)图的相关定义
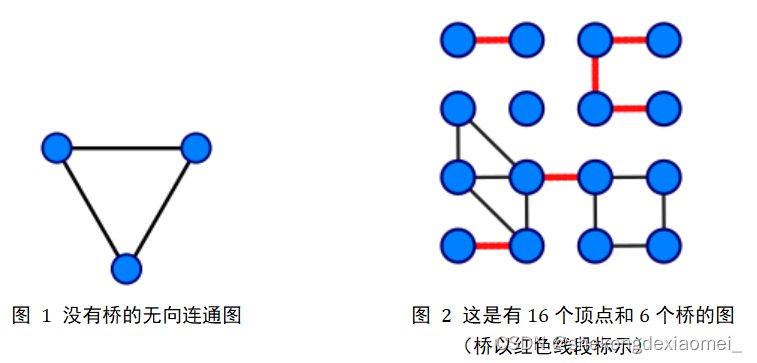
图:由顶点的有穷非空集合和顶点之间的边的集合组成。
连通图:在无向图G中,若对于任意两点x与y有路径,则称x与y连通,图G为连通图。
连通分量:非连通图的极大连通子图为连通分量。
(2)桥的定义
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。
2.解决问题
找出一个无向图中所有的桥。
要求:
(1)实现基准算法。
(2)设计的高效算法中必须使用并查集,如有需要,可以配合使用其他任何数据结构。
(3)用图2的例子验证算法正确性。
(4)使用文件 mediumG.txt和largeG.txt 中的无向图测试基准算法和高效算法的性能,记录两个算法的运行时间。
(5)设计的高效算法的运行时间作为评分标准之一。
(6)提交程序源代码。
(7)实验报告中要详细描述算法设计的思想,核心步骤,使用的数据结构。
3.实验过程
(1)基准算法
①算法原理:
| For every edge (u, v), do following |
| a) Remove (u, v) from graph b) See if the graph remains connected (We can either use BFS or DFS) c) Add (u, v) back to the graph. |
②算法伪代码:
| void jizhun(int edge_i)//遍历所有的边 |
| n1=count(); remove(edge_i);//删掉该边 n2=count(); add(edge_i);//补回刚才暂时删掉的边 if(n1!=n2) return 1;//该边是桥 return 0;//该边不是桥 |
③时间复杂度分析:
穷举删除的边需要e次,每次删除都要dfs判断连通分支数目,需要O(n+e),复杂度O(e)
对于稀疏图(e=n):复杂度为(n^2)
对于稠密图(e=n^2):复杂度为(n^4)
④小规模测试:
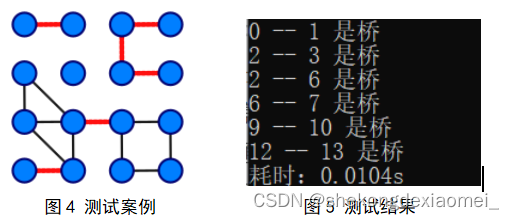
⑤不同规模下算法运行效率和理论值对比
表1 稀疏图下算法效率O(n^2)
| 1000 | 2000 | 3000 | 4000 | 5000 | |
| 实验值 | 0.0636 | 0.2768 | 0.6843 | 1.1585 | 1.6531 |
| 理论值 | 0.0636 | 0.2544 | 0.5724 | 1.0176 | 1.59 |

表2 稠密图下算法效率O(n^4)
| 100 | 150 | 200 | 250 | 300 | |
| 实验值 | 0.6469 | 3.0139 | 8.8914 | 22.2807 | 45.062 |
| 理论值 | 0.6469 | 3.274931 | 10.3504 | 25.26953 | 52.3989 |
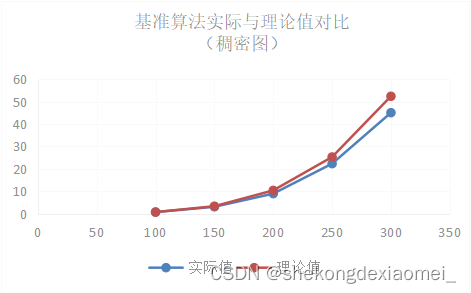
实验结果表明,基准算法解决桥问题理论值和实验值在不同数据规模下几乎相同,基准算法解决稀疏图理论分析得出的O(n^2)的平均时间复杂度是相对准确的,基准算法解决稠密图理论分析得出的O(n^4)的平均时间复杂度是相对准确的。
(2)基准法+并查集
①算法原理:
与基准法思路相同,通过删除边并计算连通分支数目来查找桥,计算连通分支时使用并查集。并查集计算连通分支数目的步骤为:枚举边,对每个边上的两点v1和v2,查询v1和v2所属的集合f1,f2,如果v1和v2不在同一个集合则合并v1和v2所属的两个集合,最后统计集合的个数,即为连通分支数目。
②算法伪代码:
| void bingchaji() |
| for u in agj[v]: f1=find(v) f2=find(u) if f1 != f2: father[f2]=f1 |
| int find(x) |
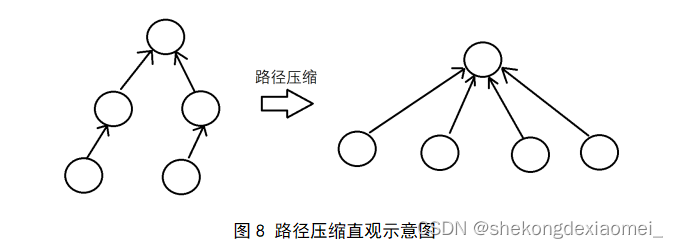
| if father[x]==x return x; father[x]=find(father[x]) //路径压缩 return father[x]; |
使用路径压缩策略,使得并查集的查询复杂度均摊下来为O(1)
③时间复杂度分析:(其中 n为顶点数,e为边数)
穷举删除的边需要e次,每次删除都用并查集判断连通分支数目,需要O(e),复杂度O(e)
对于稀疏图(e=n),复杂度为O(n2),对于稠密图(e=n2),复杂度为O(n4)
| 稀疏图 | 1000 | 2000 | 3000 | 4000 | 5000 |
| 实际值 | 0.0668 | 0.3459 | 0.6208 | 1.1796 | 1.8812 |
| 理论值 | 0.0668 | 0.2672 | 0.6201 | 1.0688 | 1.67 |

| 稠密图 | 100 | 150 | 200 | 250 | 300 |
| 实际值 | 1.119 | 4.9772 | 15.8986 | 38.1267 | 80.5864 |
| 理论值 | 1.119 | 5.664938 | 17.904 | 43.71094 | 90.639 |
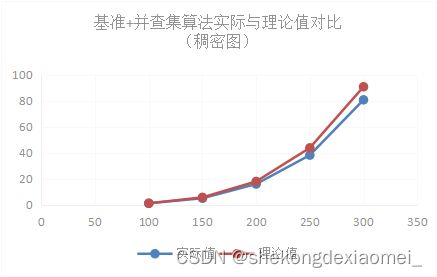
实验结果表明,基准+并查集算法解决桥问题理论值和实验值在不同数据规模下几乎相同,基准+并查集算法解决稀疏图理论分析得出的O(n^2)的平均时间复杂度是相对准确的,基准算法解决稠密图理论分析得出的O(n^4)的平均时间复杂度是相对准确的。
④优化效果
| 稀疏图 | 1000 | 2000 | 3000 | 4000 | 5000 |
| 优化前 | 0.0636 | 0.2768 | 0.6843 | 1.1585 | 1.6531 |
| 优化后 | 0.0668 | 0.3459 | 0.6208 | 1.1796 | 1.8812 |
分析得知,当数据规模较小时,算法的优化效果不明显,接下来在基准+并查集的算法基础上再设计优化算法。
(3)基准+并查集+生成树
①引入最近公共祖先(LCA)
在一棵没有环的树上,除根节点外每个节点都有其父节点和祖先节点,最近公共祖先就是两个节点在这棵树上深度最大的公共祖先节点。寻找两个节点的最近公共节点即根据两个节点的深度分别向树根方向查找,当查找到第一个相同节点时,该节点即为两个节点的最近公共祖先。
排除所有不是桥的边,剩下的即为桥。可以通过判断一条边是否在环上,进行桥的判断。树是边数最小的无环图,并且当向树上添加任意一条顶点都在树上的边,必定会形成环。而桥必定不在环上,一定存在于图的生成树上,所以除了图的生成树上的边,其他的边一定不是桥。基于这一想法,可以先构建生成树,再枚举不在生成树上的所有边,并根据最近公共祖(LCA)排除加入这些边后生成的环所在的边,最后剩下的边即为桥。
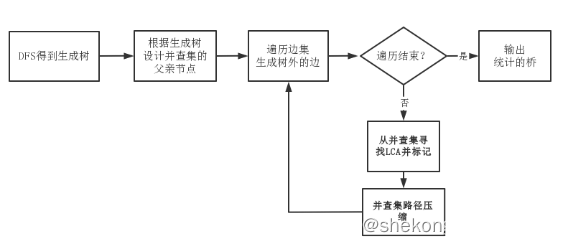
②生成树:
因为桥边一定会出现在生成树上,所以对于基准法,我们只需要枚举生成树上的边,而不需要枚举所有的边,就能找到答案。生成树优化能够使得枚举边的代价从O(e)变为O(n)。
生成树的构建:使用 DFS 遍历,并在DFS 遍历时根据得到的生成树中边前驱与后继的关系为并查集设置好各个节点的父节点。
环的搜索与桥的标记:引入最近公共祖先来保证向上寻找祖先时每条边只被经过一次。将这些在环中的边标记为非桥。对边的标记可以通过对点数组的操作来实现节省空间。
路径压缩:对于层数较深的节点,需要多次递归才能找到最近公共祖先(LCA),并且,在递归过程中一直沿着完全一样的递归路径进行递归,造成了很多无用的向上递归。运用并查集对路径进行压缩,可以降低层数较深节点的最近公共祖先(LCA)递归时间。
③时间复杂度分析
(顶点个数为n,边个数为)
DFS构建生成树时间复杂度为O(n+e);为并查集设置父节点时间复杂度为O(n);一次查找最近公共祖先最差情况下要查找n次,时间复杂度O(n) ;一次路径压缩最差情况时间复杂度也为O(n);总共需要执行e-m次查找(m为生成树边数),因此算法的总时间复杂为:
T=O(n+e)+O(n)+(e−m)×O(n)=O(en)
查找的时间复杂度O(n)是最差情况,对于大数据量级下的查找操作,经过并查集的路径压缩,很快需要查找的节点基本上父节点大部分都已经被设置为最近公共祖先(LCA)。此时,查找的时间会接近O(1)。此时有:
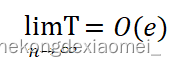
即对大数据下算法的时间效率得到了极大提升。
④伪代码
| LCA(u, v) |
| if (father[u] == v || father[v] == u) return u1 = u, v1 = v; while(true) if depth[u]>depth[v] tag[v]=0,v=father[v] else if u!=v tag[u]=0,tag[v]=0 u=father[u] v=father[v] else break unzip(u1,u),unzip(v1,v) Unzip(x, v) if father[x] == v return else tempx = x x = father[x]; father[temp] = v; Upzip(x, v) |
⑤时间效率分析

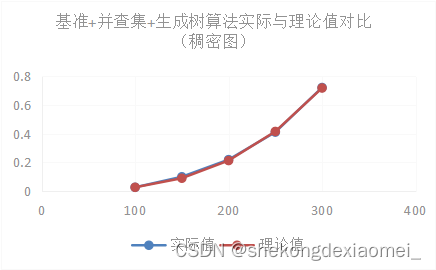

(5)大规模测试
由于largeG数据集过大,在二维数组过大时使用DFS/BFS递归时可能会出现栈空间不足而无法处理数据从而得到可行解,故先对于IDE进行栈空间的扩充。
采用优化算法对大规模测试数据进行求解:

(6)其他优化算法
Tarjan算法是一个基于深度优先搜索(DFS)的图算法,用于寻找一个有向图中的强连通分量。
伪代码:
| void Tarjan(G(E,V)) |
| function Tarjan-SCC(v): v.index = index v.lowlink = index index = index + 1 stack.push(v)
for each edge (v, w) in E: if w.index is undefined: Tarjan-SCC(w) v.lowlink = min(v.lowlink, w.lowlink) else if w is in stack: v.lowlink = min(v.lowlink, w.index)
if v.lowlink = v.index: SCC = [] repeat w = stack.pop() SCC.add(w) until w = v SCCs.add(SCC) for each vertex v in V: if v.index is undefined: Tarjan-SCC(v) |
算法效率:
| 基准算法 | 基准+并查集+生成树 | Tarjan | |
| largeG测试运行时间 | 无解 | 2.987s | 1.692s |
通过测试得知,算法效率大大提升。
除此之外,还可以加入编译优化:由于算法过程中使用了大量的STL容器,因此在编译时应该选择进行O3优化,大致可以将程序的运行时间缩短至原来的一半。




ALGO-957 P0703反置数)

)








)


)
)