1. 连通图概念
连通图:无向图任意两点之间存在通路。
强连通:有向图(前提)中,任意两点都有至少一条通路,则此图为强连通图。
弱连通图:将有向图的有向边换成无向边得到的图是连通图,则此有向图是弱连通图。
1.1 连通图和强连通图区别
连通图和强连通图的主要区别在于它们处理无向图和有向图的方式。以下是详细介绍:
连通图。 连通图的概念基于无向图,其中如果任意两个顶点之间都存在一条路径,那么整个图被称为连通图。这意味着,从任何一个顶点出发,都可以通过路径到达图中的任何其他顶点。
强连通图。 强连通图的概念则针对有向图,其中不仅要求从顶点vi到顶点vj存在路径,还要求从顶点vj到顶点vi也存在路径,对于所有顶点对vi和vj。这意味着图中不存在方向性的障碍,任意两个顶点之间可以相互到达。
简而言之,连通图关注的是无向图中顶点的连接性,而强连通图关注的是有向图中顶点的双向连接性。
2. Targan强连通分量算法
2.1 基本概念
强连通分量: 在有向图G中,如果两个顶点u,v间(u->v)有一条从u到v的有向路径,同时还有一条从v到u的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量。
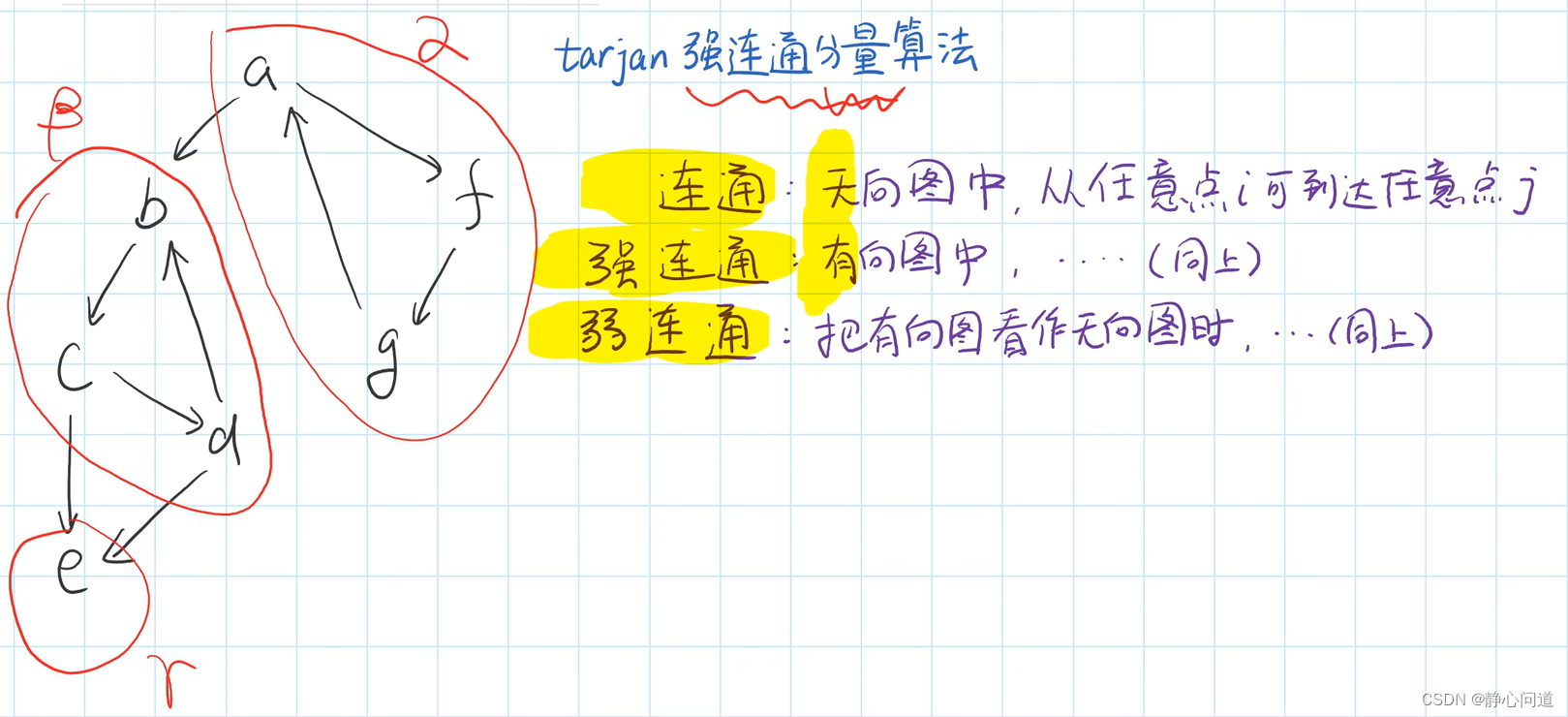
α \alpha α、 β \beta β、 γ \gamma γ 是三个强连通分量。
2.1 DFS遍历
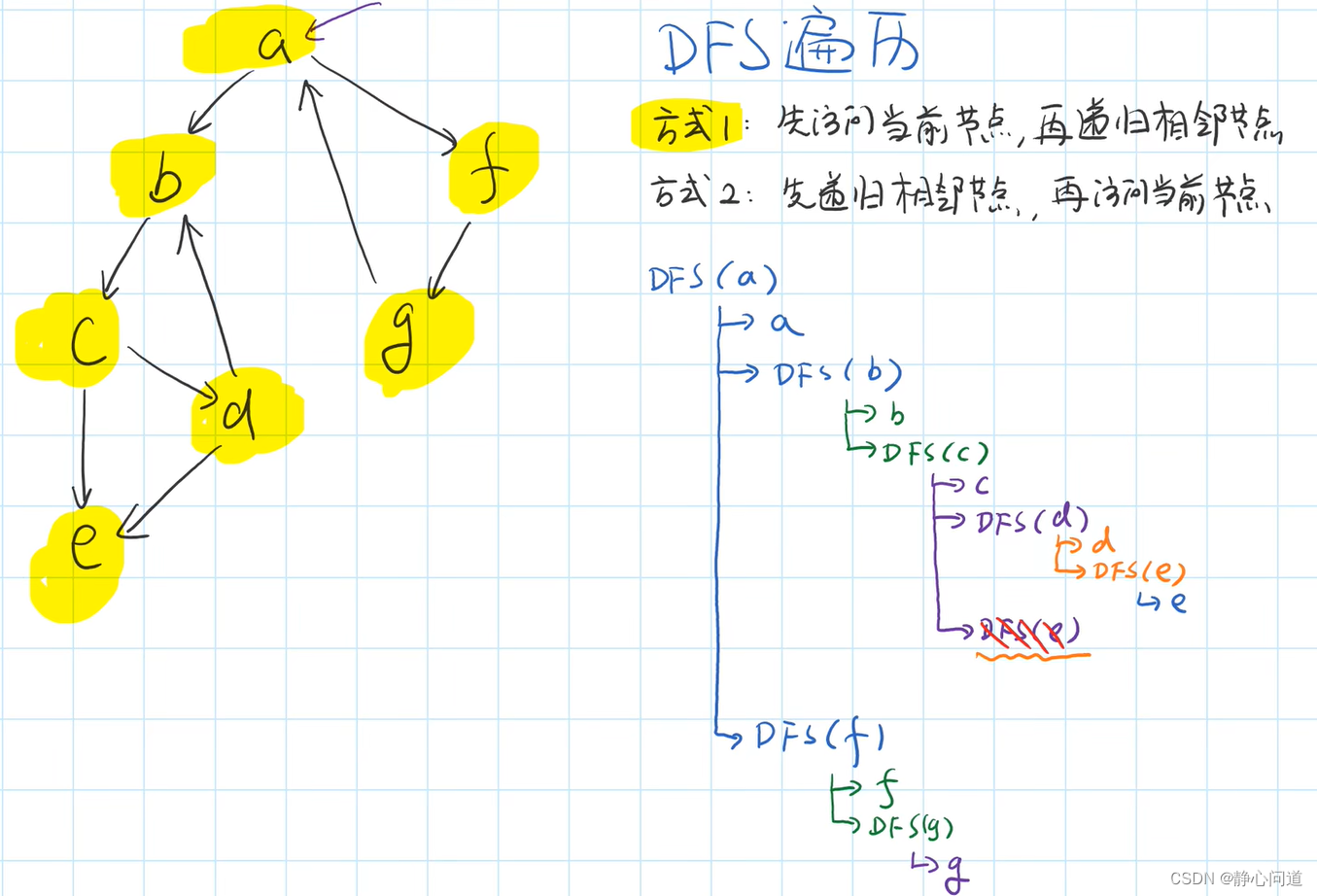
方式1可以看作前序遍历
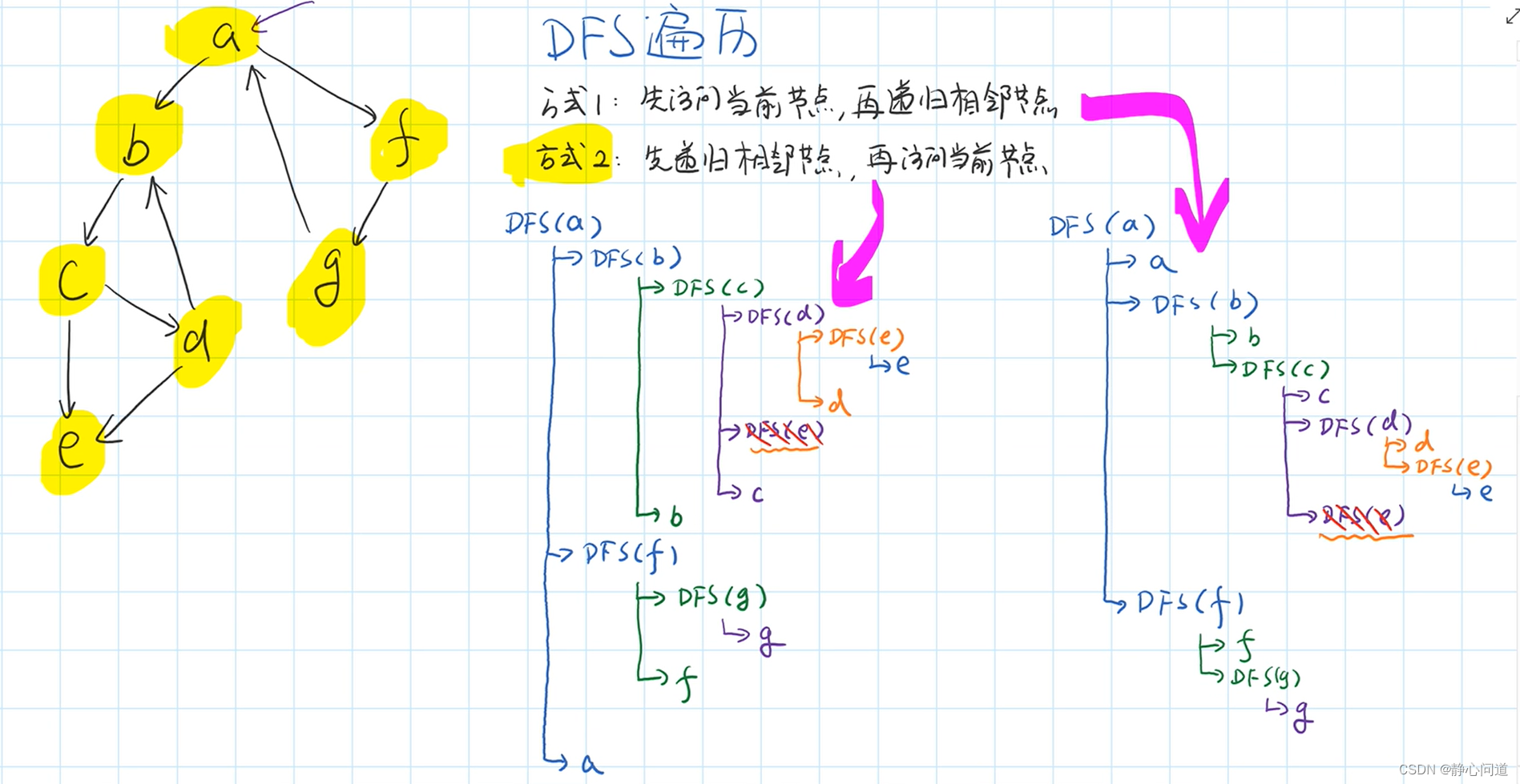
方式2可以看作后序遍历
3. 举例
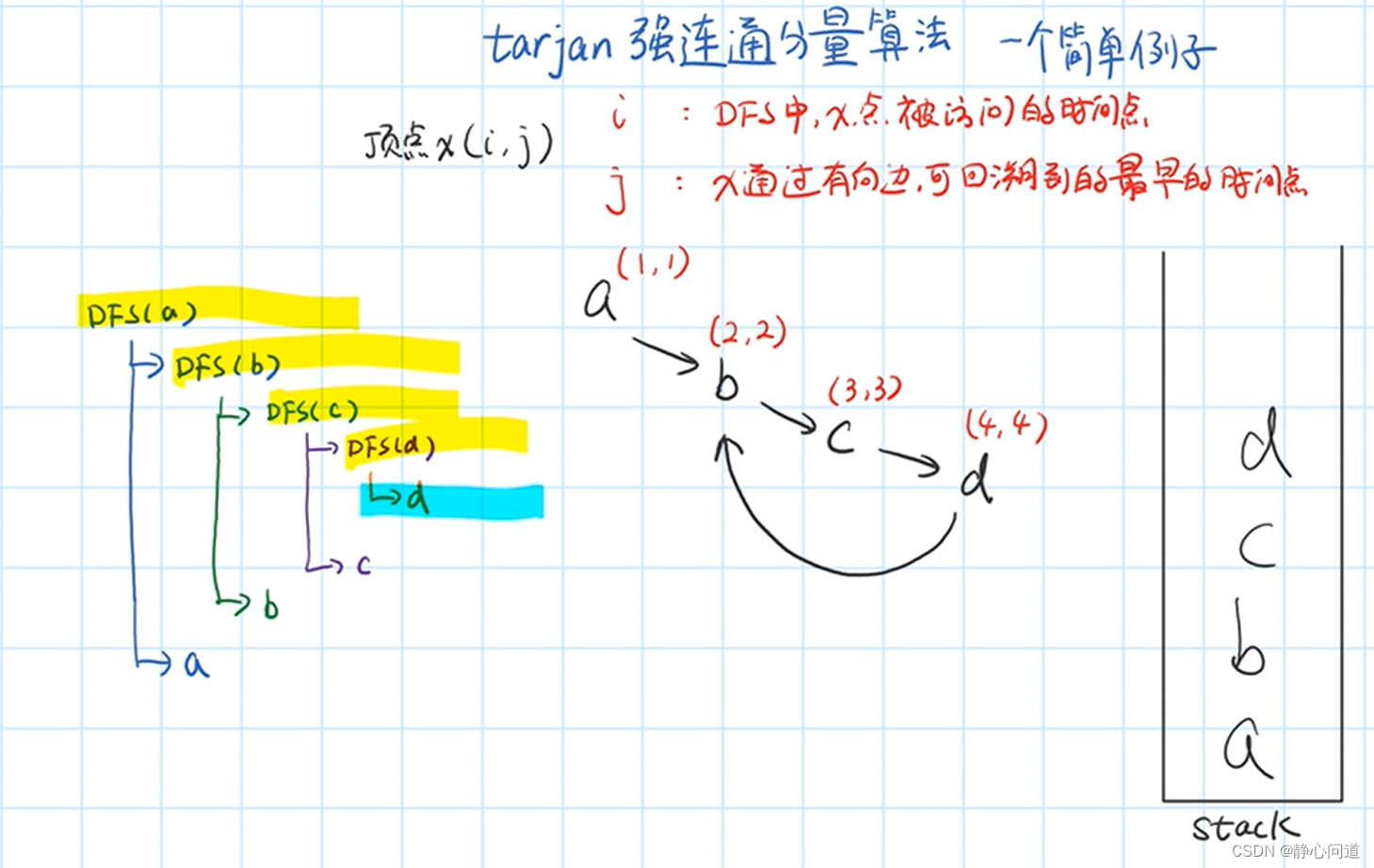
回溯,更新$j$
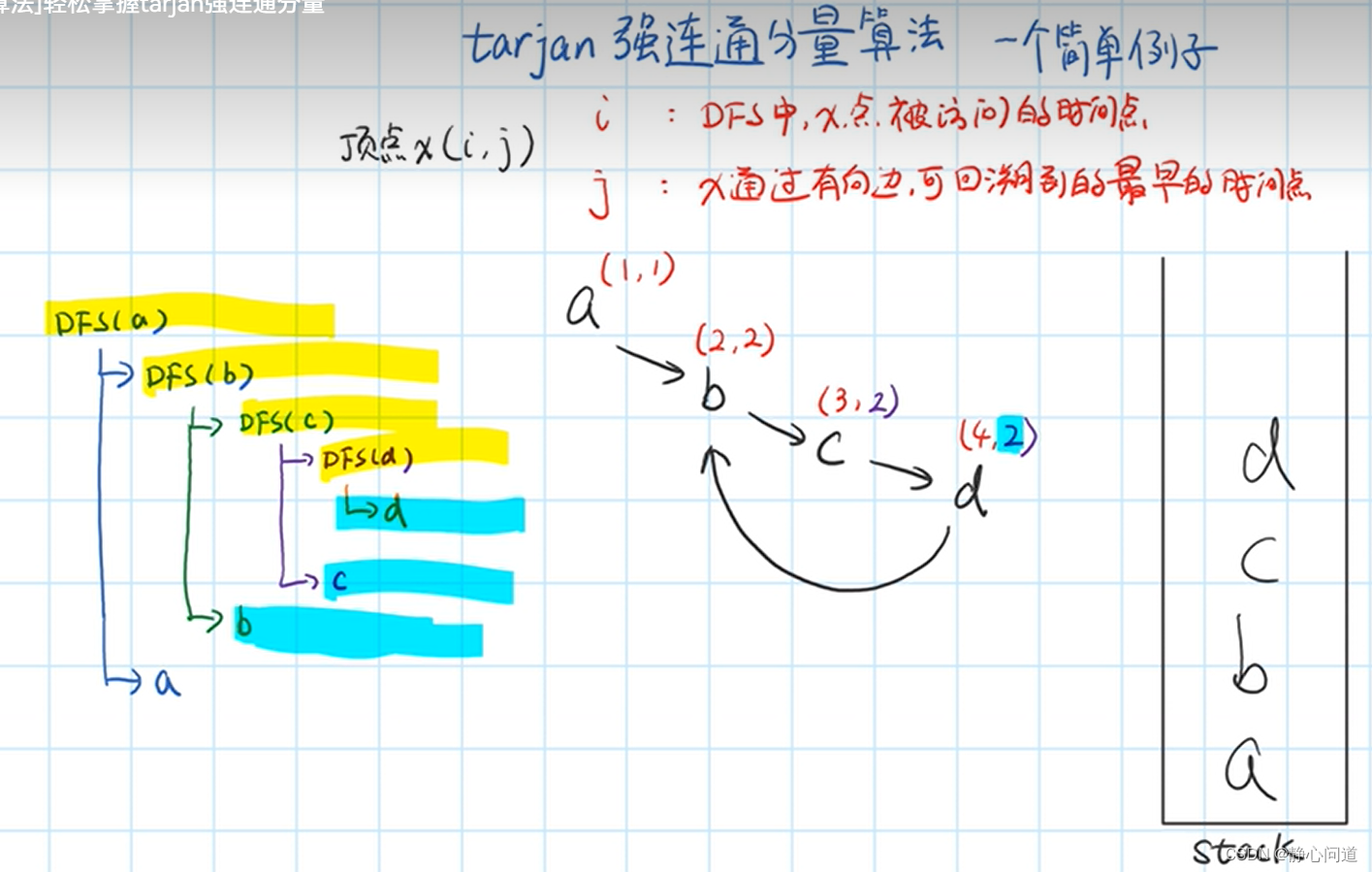
相同 j j j出栈
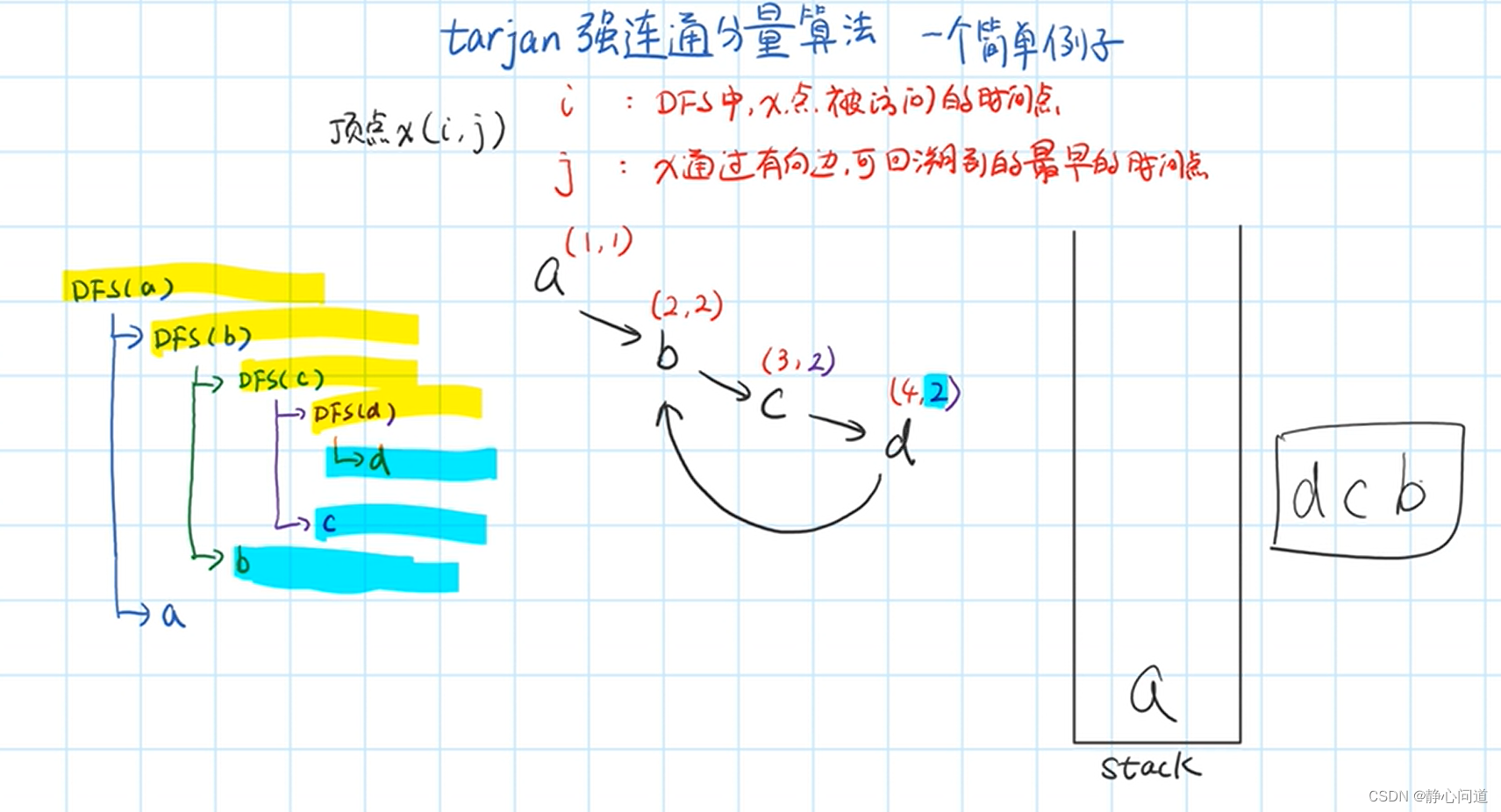
a a a也出栈,单独连通分量。
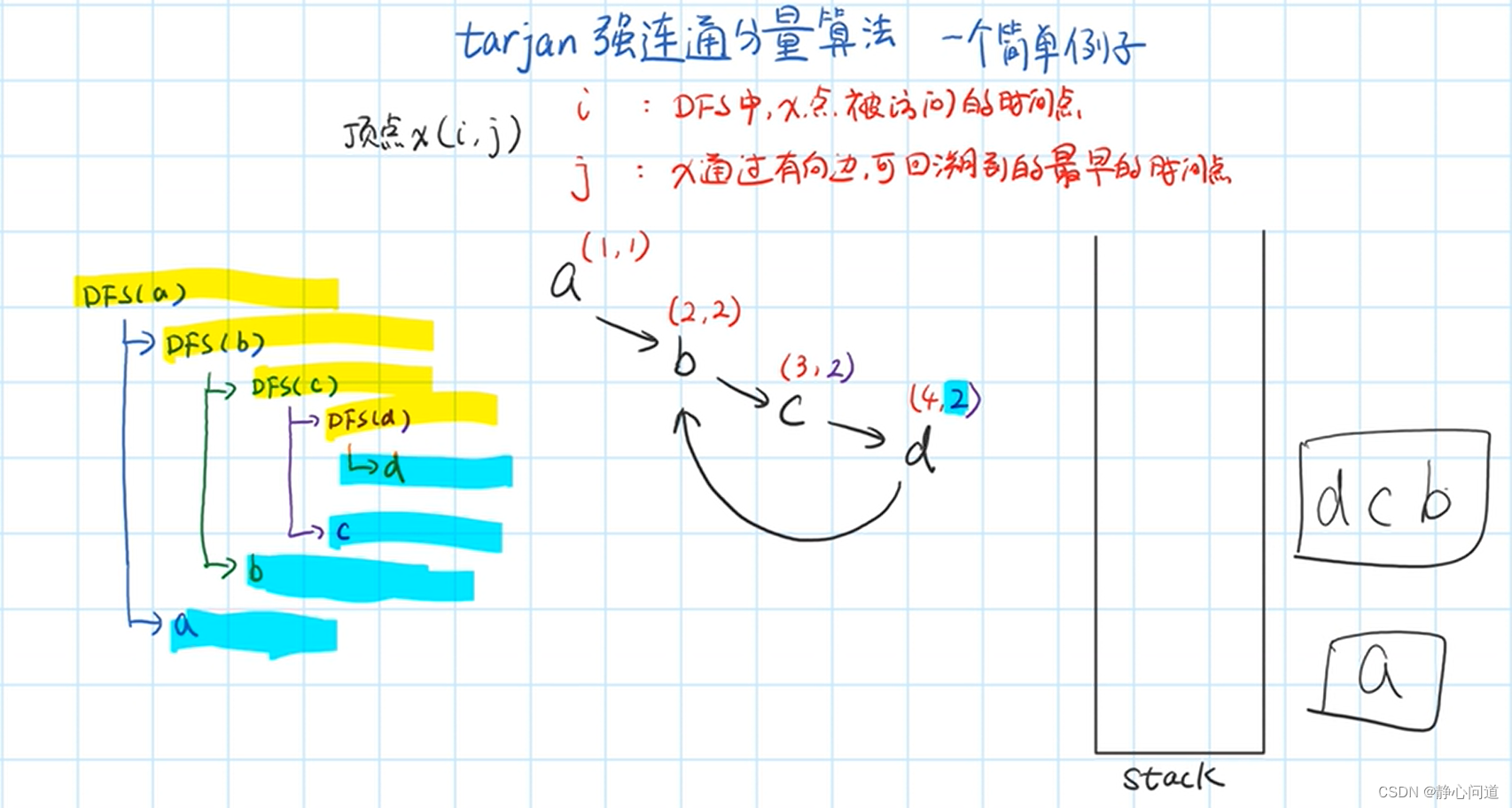
4. 代码实现
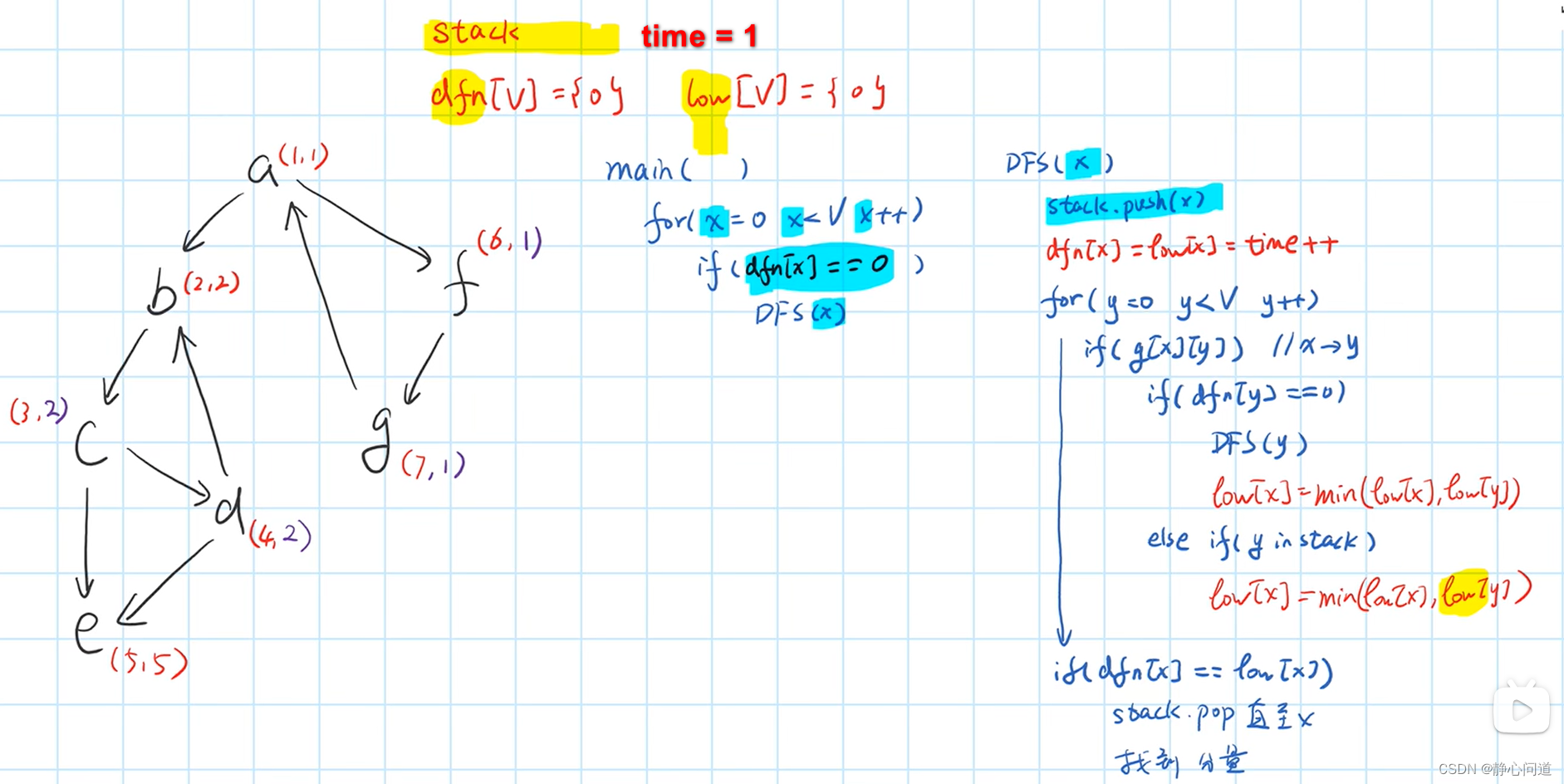
#include <bits/stdc++.h>using namespace std;#define M (INT_MAX)
#define PRINT_ARRAY(a,n) do{for(int i = 0; i < n; i++) cout<<a[i]<<"|"; cout<<endl;}while(0)/**********************************************1 → 0 → 3↑ ↙ ↓2 43 → 4 ← 6 → 2↑↓ ↓ ↗ ↓ ↙↑7 → 5 → 0 → 1
**********************************************/
// #define V (5)
// int g[V][V] =
// {
// {0,0,1,1,0},
// {1,0,0,0,0},
// {0,1,0,0,0},
// {0,0,0,0,1},
// {0,0,0,0,0}
// };#define V (8)
int g[V][V] =
{ // 0 1 2 3 4 5 6 7 {0,1,0,0,0,0,0,0},{0,0,1,0,0,0,0,0},{1,0,0,0,0,0,0,0},{0,0,0,0,1,0,0,1},{0,0,0,0,0,1,0,0},{1,0,0,0,0,0,1,0},{1,0,1,0,1,0,0,0},{0,0,0,1,0,1,0,0}
};/**********************************************强连通分量 strongly connected component
**********************************************/void tarjan_dfs(int x, int dfn[], int low[], stack<int>& s, bool in_stack[])
{static int time = 1;dfn[x] = low[x] = time++;s.push(x);in_stack[x] = true;for(int y = 0; y < V; y++){if(g[x][y]){if(0 == dfn[y]){tarjan_dfs(y, dfn, low, s, in_stack);low[x] = min(low[x], low[y]);}else if(in_stack[y])low[x] = min(low[x], dfn[y]);}}if(dfn[x] == low[x]){int tmp;do{tmp = s.top(); s.pop();in_stack[tmp] = false;cout<<tmp<<"-";}while(tmp != x);cout<<endl;}
}void scc_tarjan()
{int dfn[V] = {0}, low[V] = {0};bool in_stack[V] = {false};stack<int> s;for(int i = 0; i < V; i++)if(!dfn[i])tarjan_dfs(i, dfn, low, s, in_stack);
}int main()
{scc_tarjan();return 0;
}
参考资料:
https://www.bilibili.com/video/BV19J411J7AZ?p=1&vd_source=63c3682e66febb42e6a271165dd5a13e
https://github.com/xiaoyazi333/data-structure-and-algorithm/



)







 防腐层模式)






 从.txt文件中读取数据到矩阵)
)