一、背景

在当今科技日新月异的时代，先进电气技术正在全球范围内以前所未有的速度发展，尤其是在“控制”与“估计”两大核心技术领域的突破，对电力系统、工业自动化、智能电网、电动汽车等诸多领域产生了深远影响。本文将探讨这两项核心技术的内涵及其在先进电气技术中的融合应用。

“控制”是电气工程领域中的核心概念之一，它主要关注如何通过精确的数学模型和先进的控制算法，实现对电气系统的实时控制和优化。在先进电气技术中，现代控制理论，如自适应控制、预测控制、滑模控制、最优控制等，已经被广泛应用到电力变换、电机驱动、分布式能源管理等各种场景中。这些先进的控制技术不仅提升了电气系统的响应速度、降低了能耗，而且在复杂环境下的鲁棒性和适应性也得到了显著增强。

与此同时，“估计”技术在电气系统中的地位也同样举足轻重。在现代电气系统中，由于系统内部状态不易直接测量，因此需要借助估计技术来推测系统的隐含状态，如母线电压、电机转速、电池SOC（荷电状态）等。估计理论涵盖了一系列算法，包括卡尔曼滤波、粒子滤波、最小二乘估计、无迹卡尔曼滤波等，它们能够从有限且受噪声影响的测量数据中，提取出系统的真实状态信息。在数模混合芯片设计、电力电子变换器控制、电力系统状态估计等领域，估计技术已经成为确保系统高性能运行和智能化决策的基础。

近年来，随着信息技术、物联网、大数据和人工智能技术的发展，控制与估计的融合趋势愈发明显。例如，在智能电网中，通过融合先进控制与估计技术，可以实现对电网状态的实时感知、动态优化调度和故障快速定位；在电动汽车的电池管理系统中，精准的SOC估计结合高效的电池充放电控制策略，可以有效延长电池寿命，提高车辆续航能力。

展望未来，先进电气技术中的“控制”与“估计”将继续深化融合，依托于更加先进的传感器技术、高速计算能力以及人工智能算法，实现对电气系统更深层次的认知与控制，为绿色能源、智能制造、智能交通等重大战略领域的发展提供强有力的技术支撑。在这个过程中，技术创新和理论突破将持续推动电气工程领域的现代化和智能化进程。

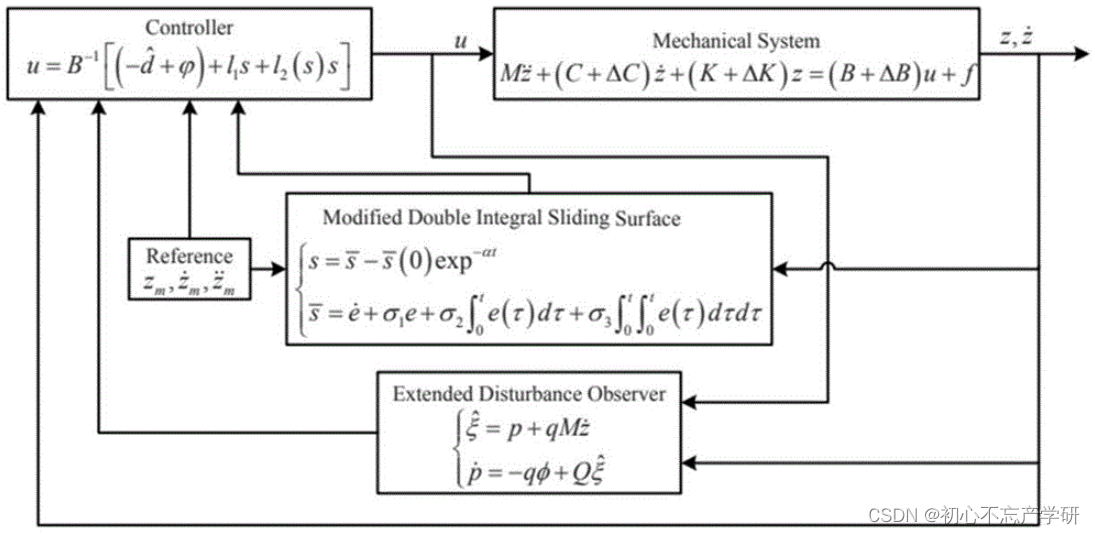
此图片来源于网络

 

二、控制角度

1. **线性系统理论**：
   - 经典控制理论：包括根轨迹法、频率响应法和Bode图等，为简单的线性系统设计控制器提供直观和简便的工具。
   - 状态空间法：由卡尔曼等人提出，强调从系统状态变量的角度出发，构建状态空间模型，进行稳定性分析、可控性与可观测性判断，以及设计状态反馈控制器。

2. **最优控制**：
   - 极大值原理：庞特里亚金提出，用变分法描述连续时间和离散时间最优控制问题，揭示最优控制策略的结构特性。
   - 动态规划：贝尔曼开创性地提出了动态规划方法，为多阶段决策过程的最优解找到了递归公式，如最短路径问题、投资决策问题等。

3. **鲁棒控制**：
   - H∞控制理论：针对系统内外部不确定性，提供了一种量化评估和改善系统鲁棒性能的方法，确保系统在各种可能的扰动下仍能维持稳定和良好的性能水平。
   - μ-分解理论：进一步细化和扩展了鲁棒控制理论，尤其是针对多输入多输出系统，确定了系统的鲁棒裕度。

4. **自适应控制**：
   - 模型参考自适应控制(MRAC)：通过实时估计和补偿系统模型误差，使系统行为尽可能接近一个预先设定的理想模型，适应系统参数变化或模型不确定性。
   - 自校正调节器(ARC)：通过在线辨识和控制相结合，实现控制器参数的自动调整，以应对模型参数的变化。

5. **非线性控制**：
   - 反馈线性化：通过设计适当的变换，将非线性系统转化为可使用线性控制理论进行设计的线性系统，如逆系统方法和动态逆控制。
   - 滑模控制：利用切换函数构造滑动模态，使系统在该模态下运行，以抵抗不确定性和扰动，特别适合于位置伺服系统和飞行控制等应用。

6. **智能控制**：
   - 模糊逻辑控制：利用模糊集合论和模糊推理机制处理不精确、不确定和非线性的控制问题，具有较强的解释性和适应性。
   - 神经网络控制：通过模拟人脑神经元网络结构，实现对复杂系统的自学习和自适应控制，尤其适用于复杂非线性系统的建模和控制。

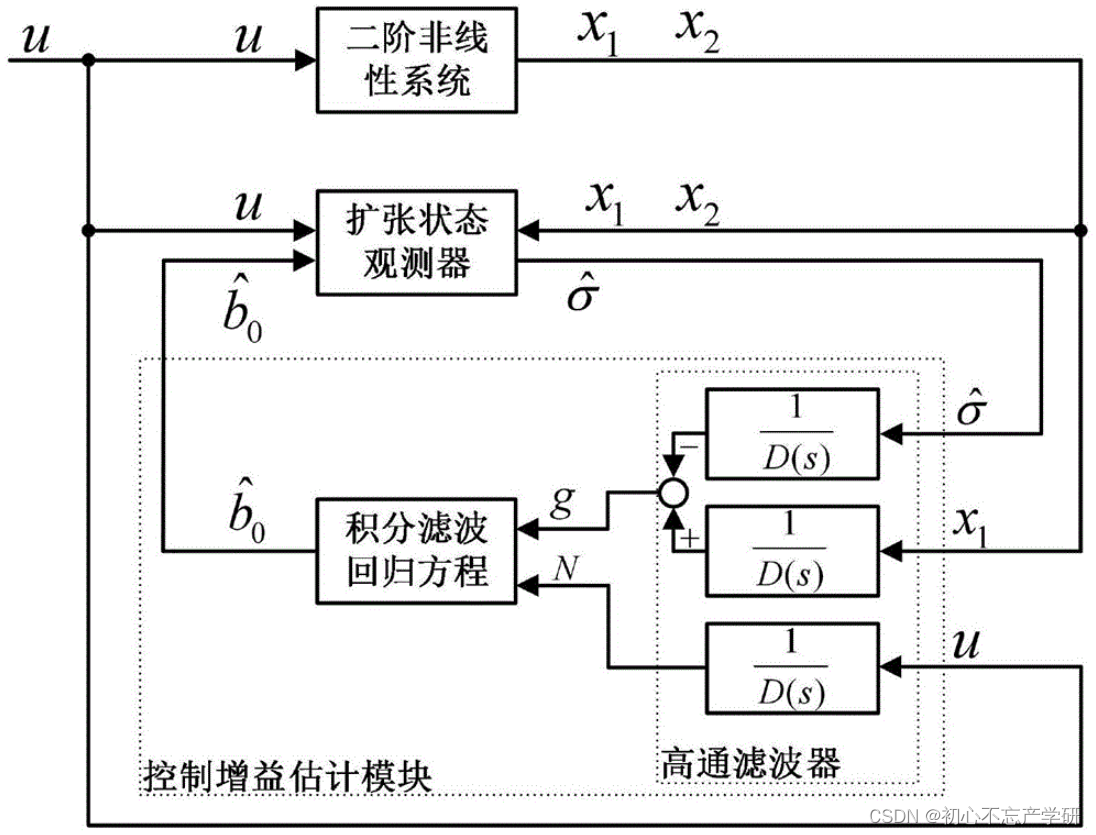
此图片来源于网络

 

三、估计角度

3.1 基本方法

1. **最小二乘估计**：
   - 最小二乘法是一种参数估计的传统方法，主要用于拟合数据模型。当模型是线性时，可以通过最小化残差平方和来估计模型参数，这种方法简单易行，广泛应用于工程实践中的数据拟合和系统参数识别。

2. **递推最小二乘估计**：
   - 在实时系统中，尤其是在数据流持续到达的场合，递推最小二乘估计（RLS）能够在线更新模型参数，避免一次性处理所有历史数据。RLS适用于处理时间序列数据，实时地对系统参数进行精确估计。

3. **最大似然估计**：
   - 最大似然估计是一种常用的参数估计方法，它假设观测数据的概率分布已知，通过最大化观测数据出现的概率（即似然函数），来确定模型参数的最优估计值。这种方法在统计学和信号处理等领域有着广泛的应用。

4. **Bayesian估计**：
   - 贝叶斯估计是一种基于先验知识和观测数据更新后验概率分布的参数估计方法。它考虑了参数的不确定性，并通过贝叶斯公式结合先验分布和似然函数来得到参数的后验分布，进而提取参数的均值、中位数或众数作为估计值。

5. **梯度搜索估计**：
   - 梯度搜索方法如梯度下降法或牛顿法等，可通过计算损失函数梯度的方向找到最优参数估计。这种方法通常用于非线性优化问题，通过迭代更新逐步逼近全局或局部最优解。

6. **增益调度和自适应滤波**：
   - 增益调度是一种根据系统当前状况动态调整控制器增益或估计器增益的技术，常用于自适应滤波器设计中。例如，在某些滤波算法中，可以根据估计误差的大小或功率谱特性改变滤波器的权重因子，以改善估计性能。

这些传统的估计方法为后续的现代估计理论如卡尔曼滤波、粒子滤波等奠定了坚实的基础，也为处理各种实际工程问题提供了有效工具。随着控制理论的发展，这些方法不断融合、优化并与其他新兴技术结合，形成了更为强大的估计理论与技术。

 

3.2 先进方法

1. **卡尔曼滤波**：
   - 线性卡尔曼滤波：卡尔曼提出的一种递推贝叶斯估计算法，用于线性动态系统状态的最优估计，被广泛应用于雷达跟踪、卫星导航和各类传感器数据融合中。

2. **扩展卡尔曼滤波**：
   - 将卡尔曼滤波推广到非线性系统，通过一阶泰勒展开对非线性系统进行线性化处理，实现了非线性系统的状态估计。

3. **无迹卡尔曼滤波**：
   - 无须对非线性系统进行线性化处理，采用统计矩变换进行递推估计，降低了由于线性化带来的误差，尤其适用于高维非线性系统的状态估计。

4. **粒子滤波**：
   - 一种基于蒙特卡洛采样的概率密度函数逼近方法，能有效处理非线性、非高斯系统的状态估计问题，特别在跟踪和定位等领域有广泛应用。

5. **系统辨识与参数估计**：
   - 最小二乘法和递推最小二乘法：用于估计系统的动态参数，通过对系统输入和输出数据进行处理，实现实时或在线参数更新。
   - 自适应滤波器：如自适应卡尔曼滤波器和自适应最小二乘滤波器，结合了自适应控制的思想，能够在线估计并补偿模型参数的变化。

6. **混合估计**：
   - 结合不同估计方法的优点，如粒子卡尔曼滤波、 Unscented Kalman Filter (UKF)等，针对特定问题灵活选择和组合不同的估计技术，提高估计精度和鲁棒性。