动态规划相当于正着想?dfs主要适用于位置的变化?
子问题!状态,状态转移方程
1 一维DP
1.1 定义

重叠子问题!转换成子问题 ,与记忆化搜索很像
1.2 例子
1.2.1 上楼梯


子问题到最终的问题只能跨一步:比如:4个台阶的话,可以从2或3走上来,但没有1!!!
1到4肯定要跨两步了

其实 就是斐波那契数列
#上楼梯
n = int(input())
dp = [0]*(n+1)
dp[1] = 1
dp[2] = 2
for i in range(3,n+1):dp[i] = dp[i-1] + dp[i-2]
print(dp[n])1.3 步骤

1.4 例题
1.4.1 破损的楼梯

# 破损的楼梯
n,m = list(map(int,input().split()))
a = list(map(int,input().split()))
vis = [0]*(n+1)
for i in a:vis[i]=1
dp = [0]*(n+1)
dp[0]=1
dp[1] =1-vis[1]
for i in range(2,n+1):if vis[i]==1:continuedp[i] = dp[i-1]+dp[i-2]
print(dp[n])
1.4.2 安全序列



##安全序列
#输入
n,k = list(map(int,input().split()))
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 2
mod = 10**9+7
for i in range(2,n+1):if i-k-1>0:#说明和这个位置相隔k的位置是存在的或许可以放置#dp[i-1]说明没有放置! dp[i-k-1]说明放置了#没有放置,则和前面的方案数一样;放置,则前间隔n个都不能放置,方案数为第(i-k-1)位置上的大小咯dp[i] = (dp[i-1]+dp[i-k-1])%modelse:dp[i] = (dp[i-1]+1)%mod
print(dp[n])
2 二维DP
2.1 定义


2.2 例题
2.2.1 数字三角形



用状态1写
##数字三角形
# 特点:第n行有n个数字
n = int(input())
a = [[0],]
dp = [[0]*(i+1) for i in range(n+1)]
for i in range(n):a.append([0] + list(map(int, input().split())))#用状态1写:(i,j)表示从(i,j)往下走的最大和
#输出的应该是dp[1][1]
for i in range(n,0,-1):for j in range(1,i+1):if i==n:dp[i][j]=a[i][j]else:dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) +a[i][j]
print(dp[1][1])# 5
# 7
# 3 8
# 8 1 0
# 2 7 4 4
# 4 5 2 6 5用状态2写
##数字三角形
# 特点:第n行有n个数字
n = int(input())
a = [[0],]
dp = [[0]*(n+1) for i in range(n+1)]
for i in range(n):a.append([0] + list(map(int, input().split())))#(i,j)表示到达(i,j)的最大和
for i in range(1,n+1):for j in range(1,i+1):if i==1:dp[1][1] = a[1][1]else:dp[i][j] = max(dp[i-1][j-1],dp[i-1][j])+a[i][j]print(max(dp[n]))2.2.2 摆花

#摆花
n,m = list(map(int,input().split()))
a = [0]+list(map(int,input().split()))
# 摆到第i个花的时候已经有j盆花了
# dp[i][j]
# 第i种花,摆0到i盆
# dp[i][j]= dp[i-1][j]+dp[i-1][j-1]+dp[i-1][j-2] +......+dp[i-1][j-i]
# 边界:dp[0][0] = 1 dp[0][1] =1 dp[0][j] = 0
# dp[1][1]=2
dp = [[1]+[0]*m for i in range(n+1)]for i in range(1,n+1):for j in range(1,m+1): #有几盆花for k in range(0,min(a[i],j)+1):dp[i][j] += dp[i-1][j-k]dp[i][j]%=10**6+7
print(dp[n][m])
2.2.3 选数异或

n,x = list(map(int,input().split()))
a = [0]+list(map(int,input().split()))
# 状态dp[i][j]表示前i个数字异或的值是j
# 状态转移: 当第i个数字选择的时候 dp[i][j] = dp[i-1][j^a[i]]
# 当第i个数字没选的时候 dp[i][j] = dp[i-1][j]
dp = [[0]*64 for i in range(n+1)]
dp[0][0] = 1
for i in range(1,n+1):for j in range(64):dp[i][j] = (dp[i-1][j]+dp[i-1][j^a[i]]) % 998244353
print(dp[n][x])3 最长上升子序列
3.1 定义
3.1.1 子序列


状态是什么?


后面的数字必须比前面的大!!

比如现在拿到的时a[2](值为4),这时前面比4小的有1和3,对应的长度分别时1和2
就选2 在2的基础上再加1
3.2 例题
3.2.1 蓝桥勇士


n = int(input())
a = [0] + list(map(int,input().split()))
dp = [1]*(n+1)# i表示选择第i个数字
# j表示前面的数字
for i in range(1,n+1):for j in range(1,i):if a[j]<a[i]:dp[i] = max(dp[j]+1 ,dp[i])print(max(dp))注意边界全是1!!!!!!!!刚开始以自己结尾一定选自己,方案数为1!!
3.2.2 合唱队形

# 最高的中间旁边依次降低
# 假设最高的站在第i个位置 i前面是上升序列 i后面是下降序列
n = int(input())
t = [0]+list(map(int,input().split()))
dp1 = [1]*(n+1) #存储最大上升子序列
dp2 = [1]*(n+1) #存储最大下降子序列
for i in range(1,n+1):for j in range(1,i):if t[j]<t[i]:dp1[i] = max(dp1[j]+1,dp1[i])
# print(dp1)
for i in range(n,0,-1):for j in range(i+1,n+1):if t[i]>t[j]:dp2[i] = max(dp2[j]+1,dp2[i])
# print(dp2)
ans = max([dp1[i]+dp2[i]-1 for i in range(1,n+1)])
print(n-ans)4 最长公共子序列
4.1 定义

对于两个数组而言的

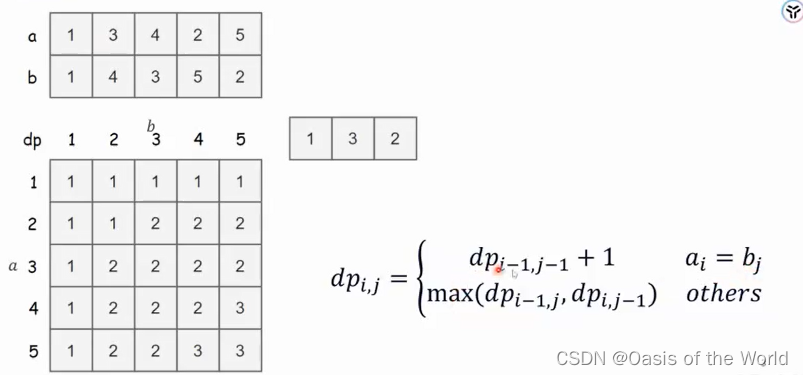
如果dp[i][j]对应的a[i]和b[j]是相等的说明 子序列的长度可以加1,在谁的基础上加1呢,左上角的就都可以!!!!【观察这个矩阵不看边界,可以知道对角线上的元素是一样的】加1肯定是在上一个对角线上咯!!!
如果对应的值不相等 说明这时的值还是上一条对角线对应的值,所以往上或左找 就是他!
怎么找出具体的公共子序列:
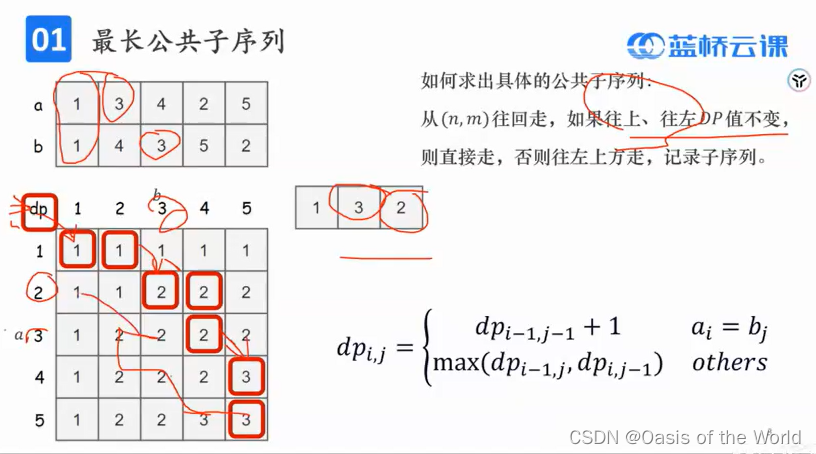
可以向上走或者想左走:说明上一条对角线的数和自己相同,没有发生状态转移,则回到这个位置,试图找到发生转移的点
不可以走的时候:说明发生的状态转移,转移一定发生在正对角线上!!!
4.2 例题

def output(a):n = len(a)for i in range(0,n):print(" ".join(map(str,a[i][0:])))n,m = list(map(int,input().split()))
a = [0]+list(map(int,input().split()))
b = [0]+list(map(int,input().split()))
dp = [[0]*(m+1) for i in range(n+1)]#状态
for i in range(1,n+1):for j in range(1,m+1):if a[i] == b[j]:dp[i][j] = dp[i-1][j-1] +1else:dp[i][j] = max([dp[i-1][j],dp[i][j-1]])
# output(dp)
print(dp[n][m])








)
开发环境搭建)


 - IAB/MRC及《增强现实广告效果测量指南1.0》)





