---

👨‍💻个人主页：@元宇宙-秩沅

👨‍💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅!

👨‍💻 本文由 秩沅 原创

👨‍💻 收录于专栏：unityUI专题篇

---

⭐⭐

---

---

🎶前言——模型转化工具介绍

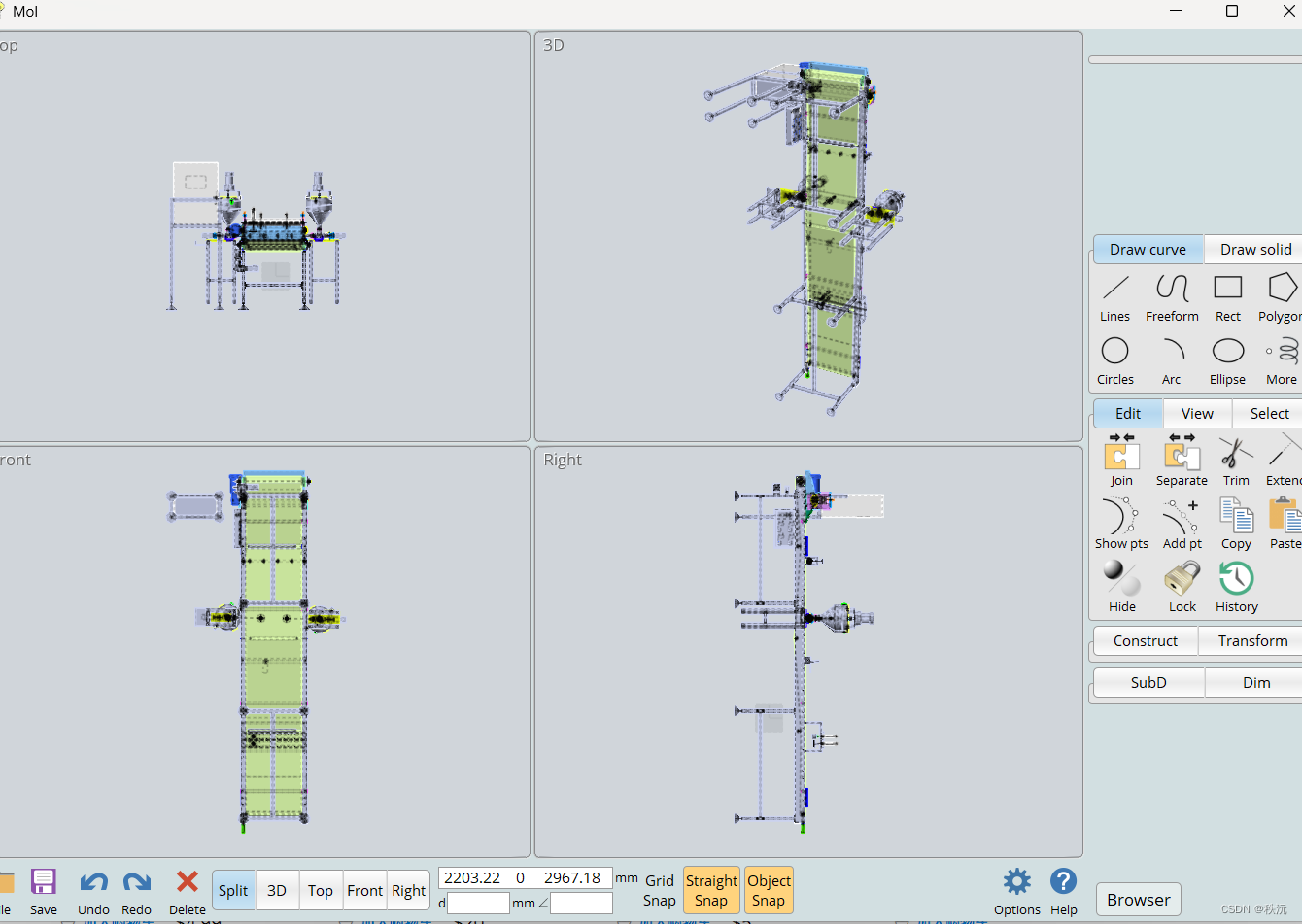
MoI 4.0 beta是指Moment of Inspiration（创意时刻）软件的测试版本。Moment of Inspiration是一款由Michael Gibson开发的3D建模软件，也被称为MoI。它使用非常直观的界面和简化的工具，使用户能够轻松地创建复杂的3D模型。MoI 4.0 beta是该软件的测试版本，意味着它是在正式发布之前的一个可供用户测试和准备反馈的版本。

这是一项可将STP，IGS，c4D等工业模型转化成任意模型格式的轻量级工具,下载包放在文章顶部

---

🅰️

---

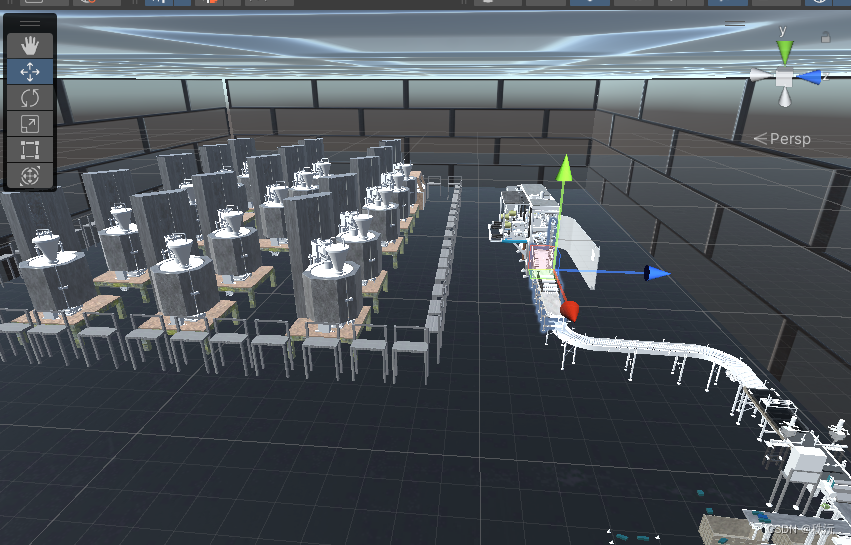
🎶（A）场景搭建

---

---

🎶（B）车间搭建

---

---

每日一记 ## 🎶（A） 四元数

特点

1，绕着某个轴转x度，轴可以是任意轴（轴-角对）
2，避免了欧拉角中万向节死锁的问题
3，避免了欧拉角中角度变化不在（-180，180）范围内的问题

• 四元数解决了欧拉角中万向节死锁的问题
• 当Unity中transform的X轴为90度是发生万向节死锁，此时不管移动y轴还是z轴，物体都往X轴进行旋转

---

原理公式

假定四元数Q绕着n轴旋转β度

 //计算原理_绕x轴旋转60度Quaternion q = new Quaternion(Mathf.Sin(30 * Mathf.Deg2Rad),0, 0, Mathf.Cos(30 * Mathf.Deg2Rad));

---

直接简单公式

• Quaternion.AngleAxis（角度数值，轴（向量））

//绕x轴旋转60度Quaternion q = Quaternion.AngleAxis(60, Vector3.right);

---

API常用

1.四元数和欧拉角转换

• 欧拉角转四元数
  Quaternion A = Quaternion.Euler(60, 0, 0);

• 四元数转欧拉角
  A.eulerAngles

---

2.旋转

四元数相乘代表旋转四元数

//四元数旋转方法
transform.rotation *= Quaternion.AngleAxis(30,vector3.forword);

---

3.单位化四元数

• [1,(0,0,0)]和[-1,(0,0,0)]都是单位四元数
  表示没有旋转量
• Quaternion.identity _用于对象角度初始化

Instantiate(XXXX, Vector3.zero, Quaternion.identity);

---

4.四元数的差值运算

• 特点: Lerp() 和Slerp（）；官方建议一般用Slerp();
• 先快后慢旋转

transform.rotation = Quaternion.Slerp(transform.rotation, 
target.rotation, Time.deltaTime);

• 匀速旋转—— time>=1 到达目标

  time += Time.deltaTime;B.transform.rotation = Quaternion.Slerp(start,target.rotation, time);

---

5.四元数的旋转看向——LookAt的本质

Quaternion A = Quaternion.LookRotation(B.position - A.position);

    //B - A = AB 向量 ，所以传入的是向量

transform.rotation = A;

【Unity每日一记】进行发射，位置相关的方法总结
【Unity每日一记】摄像机相关向量代码API大全

---

---

⭐相关文章⭐

---

⭐【2023unity游戏制作-mango的冒险】-6.关卡设计

⭐【2023unity游戏制作-mango的冒险】-5.攻击系统的简单实现

⭐【2023unity游戏制作-mango的冒险】-4.场景二的镜头和法球特效跟随

⭐【2023unity游戏制作-mango的冒险】-3.基础动作和动画API实现

⭐【2023unity游戏制作-mango的冒险】-2.始画面API制作

⭐【2023unity游戏制作-mango的冒险】-1.场景搭建

⭐“狂飙”游戏制作—游戏分类图鉴（网易游学）

⭐本站最全-unity常用API大全（万字详解），不信你不收藏

---

---

你们的点赞👍 收藏⭐ 留言📝 关注✅是我持续创作，输出优质内容的最大动力！