软件设计师27--规范化理论
- 考点1:规范化理论基本概念
- 函数依赖
- 规范化理论--Amstrong公理体系
- 候选键
- 主属性与非主属性
- 例题:
- 考点2:范式判断
- 规范化理论
- 规范化理论 - 范式
- 例题:
- 考点3:范式分解
- 保持函数依赖分解
- 无损分解
- 模式分解-表格法
- 无损分解 - 公式法
- 例题:
考点1:规范化理论基本概念
函数依赖
设R(U)是属性U上的一个关系模式,X和Y是U的子集,r为R的任一关系,如果对于r中的任意两个元组u,v,只要有u[X]=v[X],就有u[Y]=v[Y],则称X函数决定Y,或称Y函数依赖于X,记为X->Y。
关系模式:R(A,B,C)
依赖集1:{AB->C,A->C}
部分函数依赖:A可以确定C,(A,B)也可以确定C。(A,B)中的一部分(即A)可以确定C,称为部分函数依赖。
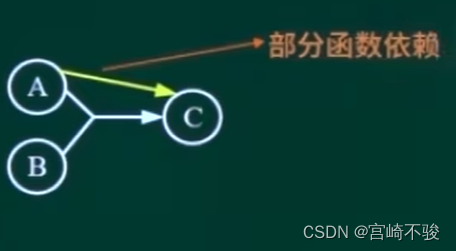
依赖集2:{A->B,B->C}
传递函数依赖:当A和B不等价时,A可确定B,B可确定C,则A可以确定C,是传递函数依赖
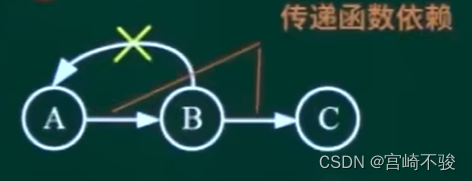
由:A->B,B->C,可得出A->C。此为传递函数依赖
规范化理论–Amstrong公理体系
关系模式R<U,F>来说有以下的推理规则:
A1.自反律(Reflexivity):若Y⊂ X⊂ U,则X→Y成立。
A2.增广律(Augmentation):若Z⊂ U且X→Y,则XZ→YZ成立。
A3.传递律(Transitivity):若X→Y且Y→Z,则X→Z成立。
根据A1,A2,A3这三条推理规则可以得到下面三条推理规则:
合并规则:由X→Y,X→Z,有X→YZ。(A2,A3)
伪传递规则:由X→Y,WY→Z,有XW→Z。(A2,A3)
分解规则:由X→Y及Z⊂ Y,有X→Z。(A1,A3)
候选键
候选键:唯一标识元组,且无冗余,任选一个为主键
外键:其他关系的主键

例1:给定关系R(A1、A2、A3)上的函数依赖集F={A1->A2,A3->A2,A2->A3,A2->A4},R的候选键关键字为(A)。
A、A1
B、A1A3
C、A1A3A4
D、A1A2A3
例2:关系模式P(A、B、C、D、E、F、G、H、I、J)满足下列函数依赖:FD={ABD->E,AB->G,B->F,C->J,CJ->I,G->H},求候选码?。
(ABCD)
例3:关系R(A、B、C)满足下列函数依赖:F={B->C,B->A,A->BC},关系R的候选关键字为(B)。
A、若X→Y,X→Z,则X->YZ为F所蕴涵
B、若X→Y,WY→Z,则XW→Z为F所蕴涵
C、若X->Y,Y->Z为F所蕴涵,则X->Z为F所蕴涵
D、若X->Y为F所蕴涵,且Z∈U,则XZ->YZ为F所蕴涵
主属性与非主属性
定义:组成候选码的属性就是主属性,其他的就是非主属性。
例:关系模式CSZ(CITY,ST,ZIP),其属性组上的函数依赖集为:F={(CITY,ST)->ZIP,ZIP->CITY},其中CITY表示城市,ST表示街道,ZIP表示邮政编码。
候选键为:(ST,CITY),(ST,ZIP)
主属性为:CITY,ST,ZIP
例题:
1、若给定的关系模式为R,U={A,B,C},F={AB->C,C->B},则关系R(B)。
A、有2个候选关键字AC和BC,并且有3个主属性
B、有2个候选关键字AC和AB,并且有3个主属性
C、只有一个候选关键字AC,并且有1个非主属性和2个主属性
D、只有一个候选关键字AB,并且有1个非主属性和2个主属性
2、给定关系模式R(U,F),其中:U为关系模式R中的属性集,F是U上的一组函数依赖。假设U=[A1,A2,A3,A4],F={A1->A2,A1A2->A3,A1->A4,A2->A4},那么关系R的主键应为(A)。函数依赖集F中的(C)是冗余的。
A、A1
B、A1A2
C、A1A3
D、A1A2A3
A、A1->A2
B、A1A2->A3
C、A1->A4
D、A2->A4
3、给定关系模式R<U,F>,其中U为属性集,F是U上的一组函数依赖,那么Armstrong公理系统的伪传递律是指(B)。
A、A1
B、A1A2
C、A1A3
D、A1A2A3
考点2:范式判断
规范化理论
关系模式R(学生姓名,选修课程名,任课教师名,任课教师地址)
| 学生姓名 | 选修课程名 | 任课教师名 | 任课教师地址 |
|---|---|---|---|
| 张三 | 数学 | 王一新 | 五一路107号 |
| 李四 | 数学 | 王一新 | 五一路107号 |
| 王五 | 数学 | 王一新 | 五一路107号 |
| 赵六 | 数学 | 王一新 | 五一路107号 |
| …… | …… | …… | …… |
关系模式R存在问题:
- 数据冗余
- 修改异常
- 插入异常
- 删除异常
规范化理论 - 范式
第一范式(1NF):在关系模式R中,当且仅当所有域只包含原子值,即每个属性都是不可再分的数据项,则称关系模式R是第一范式。
思考题:关系模式R(系名称,高级职称人数)是否满足1NF,如果不满足,应如何调整?
| 系名称 | 高级职称人数 | |
| 教授 | 副教授 | |
| 计算机系 | 6 | 10 |
| 电子系 | 3 | 5 |
调整为:系名称,教授人数,副教授人数,高级职称总人数
第二范式(2NF):当且仅当关系模式R是第一范式(1NF),且每一个非主属性完全依赖候选键(没有不完全依赖)时,则称关系模式R是第二范式。
思考题:关系模式SC(学号,课程号,成绩,学分),其中:(学号,课程号)->成绩,课程号->学分,会存在那些问题(从数据冗余、更新异常、插入异常、删除异常这几个方面来考虑),解决方案是什么?

解析:
- 找候选键(学号,课程号)
- 找非主属性(成绩,学分)
调整为:(课程,学分)、(学号,课程号,成绩)
第三范式(3NF):当且仅当关系模式R是第二范式(2NF),且R中没有非主属性传递依赖于候选键时,则称关系模式R是第三范式。
思考题:学生关系(学号,姓名,系号,系名,系位置)各属性分别代表学号,姓名,所在系号,系名称,系地址。思考该关系模式会存在哪些问题(从数据冗余、更新异常、插入异常、删除异常这几个方面来考虑),解决方案是什么?

解析:
- 找候选键(学号)
- 找非主属性
- 2NF
- 3NF
调整为:(系号,系名,系位置)、(学号,姓名,学号)
BC范式(BCNF):设R是一个关系模式,F是它的依赖集,R属于BCNF当且仅当其F中每个依赖的决定因素必定包含R的某个候选码。
例:关系模式STJ(S,T,J)中,S表示学生,T表示老师,J表示课程。每一老师只教一门课程。每门课程有若干老师,某一学生选定某门课程,就对应一个固定老师。
T->J
SJ->T
- 候选键 SJ,ST
- 非主属性 没有
- 2NF 满足
- 3NF 满足

1NF ⊇ 2NF ⊇ 3NF ⊇ BCNF
| 范式 | 属性不可再分 | 非主属性部分函数依赖于候选键 | 非主属性传递函数依赖于候选键 | 函数依赖左侧决定因素包含候选键 |
|---|---|---|---|---|
| 1NF | √ | 存在 | ||
| 2NF | √ | 不存在 | 存在 | |
| 3NF | √ | 不存在 | 不存在 | 不满足 |
| BCNF | √ | 不存在 | 不存在 | 满足 |
例题:
1、某公司数据库中的元件关系模式为P(元件号,元件名称,供应商,供应商所在地,库存量),函数依赖集F如下所示:F={元件号→元件名称,(元件号,供应商)→库存量,供应商→供应商所在地}
元件关系的主键为(B),该关系存在冗余以及插入异常和删除异常等问题。为了解决这一问题需要将元件关系分解(C),分解后的关系模式可以达到(C)。
A、元件号,元件名称
B、元件号,供应商
C、元件号,供应商所在地
D、供应商,供应商所在地
A、元件1(元件号,元件名称,库存量)、元件2(供应商,供应商所在地)
B、元件1(元件号,元件名称)、元件2(供应商,供应商所在地,库存量)
C、元件1(元件号,元件名称)、元件2(元件号,供应商,库存量)、元件3(供
应商,供应商所在地)
D、 元件1(元件号,元件名称)、元件2(元件号,库存量)、元件3(供应商,供应商所在地)、元件4(供应商所在地,库存量)
A、1NF
B、2NF
C、3NF
D、4NF
考点3:范式分解
保持函数依赖分解
设数据库模式ρ={R1,R2,…,Rk}是关系模式R的一个分解,F是R上的函数依赖集,ρ中每个模式Ri上的FD集是Fi。如果{F1,F2,…,Fk}与F是等价的(即相互逻辑蕴涵),那么称分解ρ保持FD。
例:设关系模式R(U,F),其中U={A,B,C,D,E},F={A->BC,C->D,BC->E,E->A},则分解ρ={R1(ABCE),R2(CD)}是否保持函数依赖?而分解ρ={R1(ABE),R2(CD)}是否保持函数依赖?
R1(ABCE) F1={A->BC,BC->E,E->A}
R2(CD) F2={C->D}
分解ρ={R1(ABCE),R2(CD)}保持函数依赖
分解ρ={R1(ABE),R2(CD)}不保持函数依赖
例:设关系模式R(U,F),其中U={A,B,C},F={A->B,B->C,A->C},则分解ρ={R1(AB),R2(BC)},是否保持函数依赖?
R1(AB)F1={A->B}
R2(BC)F2={B->C}
F’={A->B,B->C => A->C}
解ρ={R1(AB),R2(BC)},保持函数依赖
无损分解
什么是有损,什么又是无损?
有损:不能还原
无损:可以还原
无损连接分解:指将一个关系模式分解成若干各关系模式后,通过自然连接等运算仍能还原到原来的关系模式
思考题:
有关系模式:成绩(学号,姓名,课程号,课程名,分数)
函数依赖:学号->姓名,课程号->课程名,(学号,课程号)->分数
若将其分解为:
成绩(学号,课程号,分数)
学生(学号,姓名)
课程(课程号,课程名)
请思考该分解是否为无损分解?
由于有:学号->姓名,所以:
成绩(学号,课程号,分数,姓名)
由于有:课程号->课程名,所以:
成绩(学号,课程号,分数,姓名,课程名)
模式分解-表格法
将一个具有函数依赖:学号->姓名,课程号->课程名,(学号,课程号)->分数的关系模式:成绩(学号,姓名,课程号,课程名,分数),分解为:成绩(学号,课程号,分数);学生(学号,姓名);课程(课程号,课程名)。
初始表如下:

根据学号->姓名,对上表进行处理,将第一行第二行属性改成符号√ ̄;然后考虑课程号->课程名,将第一行第四行属性改成符号√ ̄,得下表:
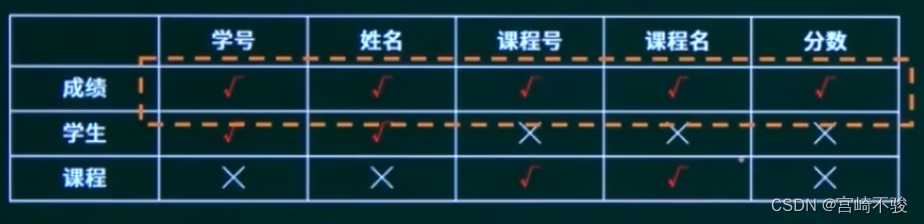
从上图中可以看出,第一行已全部为√ ̄,因此本次R分解是无损连接分解。
例:设R=ABC,F={A->B},则分解ρ1={R1(AB),R2(AC)}与分解ρ2={R1(AB),R3(BC)}是否都为无损分解?
| A | B | C | |
|---|---|---|---|
| R1(AB) | √ | √ | × |
| R2(AC) | √ | × | √ |
分解ρ1={R1(AB),R2(AC)}保持函数依赖,并且无损分解
| A | B | C | |
|---|---|---|---|
| R1(AB) | √ | √ | × |
| R3(BC) | × | √ | √ |
分解ρ2={R1(AB),R3(BC)}保持函数依赖,有损分解
无损分解 - 公式法
定理:如果R的分解为ρ={R1,R2},F为R所满足的函数依赖集合,分解ρ具有无损连接性的充分必要条件是:
R1∩R2->(R1-R2)或 R1∩R2->(R2-R1)
其中,R1∩R2表示模式的交,为R1与R2中公共属性组成,R1-R2或R2-R1表示模式的差集,R1-R2表示R1中去除R1和R2的公共属性所组成。当模式R分解成两个关系模式R1和R2时,如果R1与R2的公共属性能函数决定R1中或R2中的其他属性,这样的分解就具有无损连接性。
例:设R=ABC,F={A->B},则分解ρ1={R1(AB),R2(AC)}与分解ρ2={R1(AB),R3(BC)}是否都为无损分解?
R1∩R2=A
R1-R2=B
R2-R1=C
ρ1={R1(AB),R2(AC)}为无损分解
R1∩R3=B
R1-R3=A
R3-R1=C
ρ2={R1(AB),R3(BC)}为有损分解
例题:
1、设关系模式R(U,F),其中:U={A,B,C,D,E},F={A->B,DE->B,CB->E,E->A,B->D}。(D)为关系模式R的候选关键字。分解(D)是无损连接,并保持函数依赖的。
A、AB
B、DE
C、DB
D、CE
A、ρ={R1(AC),R2(ED),R3(B)}
B、ρ={R1(AC),R2(E),R3(DB)}
C、ρ={R1(AC),R2(ED),R3(AB)}
D、ρ={R1(ABC),R2(ED),R3(ACE)}
A选项表格法为:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| R1(AC) | √ | × | √ | × | × |
| R2(ED) | × | × | × | √ | √ |
| R3(B) | × | √ | × | × | × |
C选项表格法为:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| R1(AC) | √ | × | √ | × | × |
| R2(ED) | × | × | × | √ | √ |
| R3(AB) | √ | √ | × | × | × |
D选项表格法为:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| R1(ABC) | √ | √ | √ | × | × |
| R2(ED) | × | × | × | √ | √ |
| R3(ACE) | √ | × | √ | × | √ |
选项A不保持函数依赖,有损
选项B不保持函数依赖,有损
选项C不保持函数依赖,有损
选项D不保持函数依赖,无损
注:选项D并不完全正确,如果选项中没有正确答案的话,要选择最接近的答案








)










