目录

 1.图的定义和术语

2.案例引入 

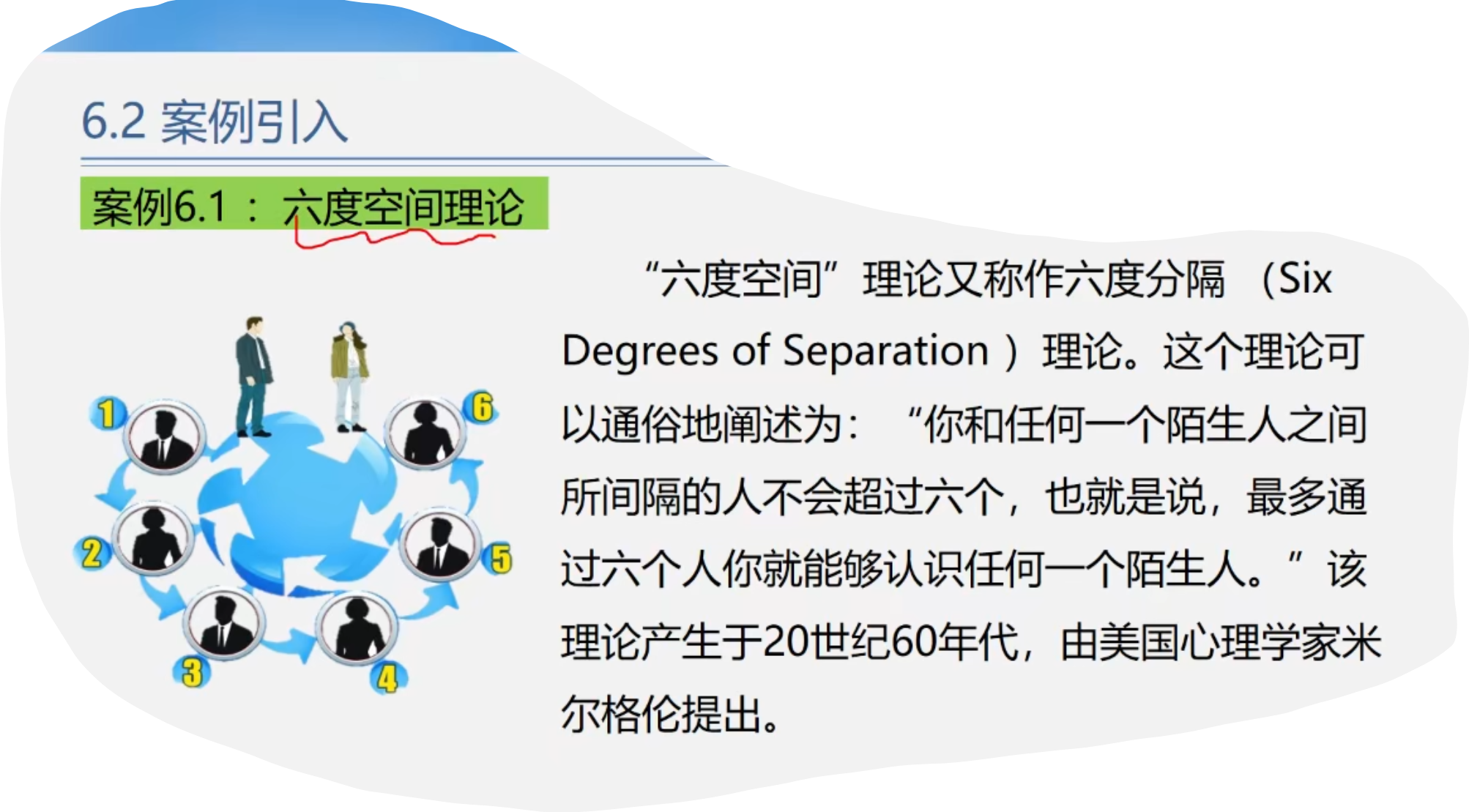
1.六度空间理论

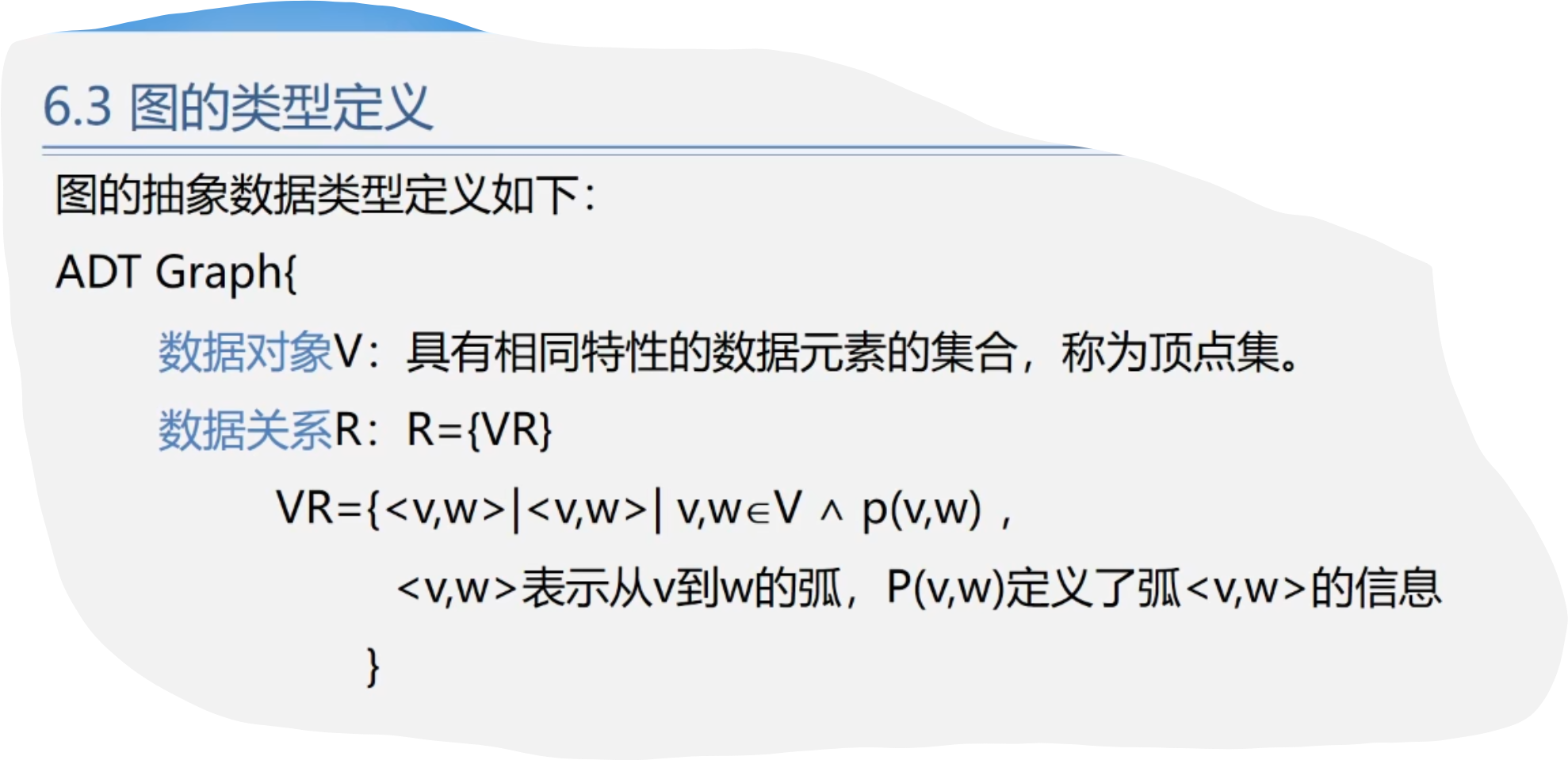
3.图的类型定义 

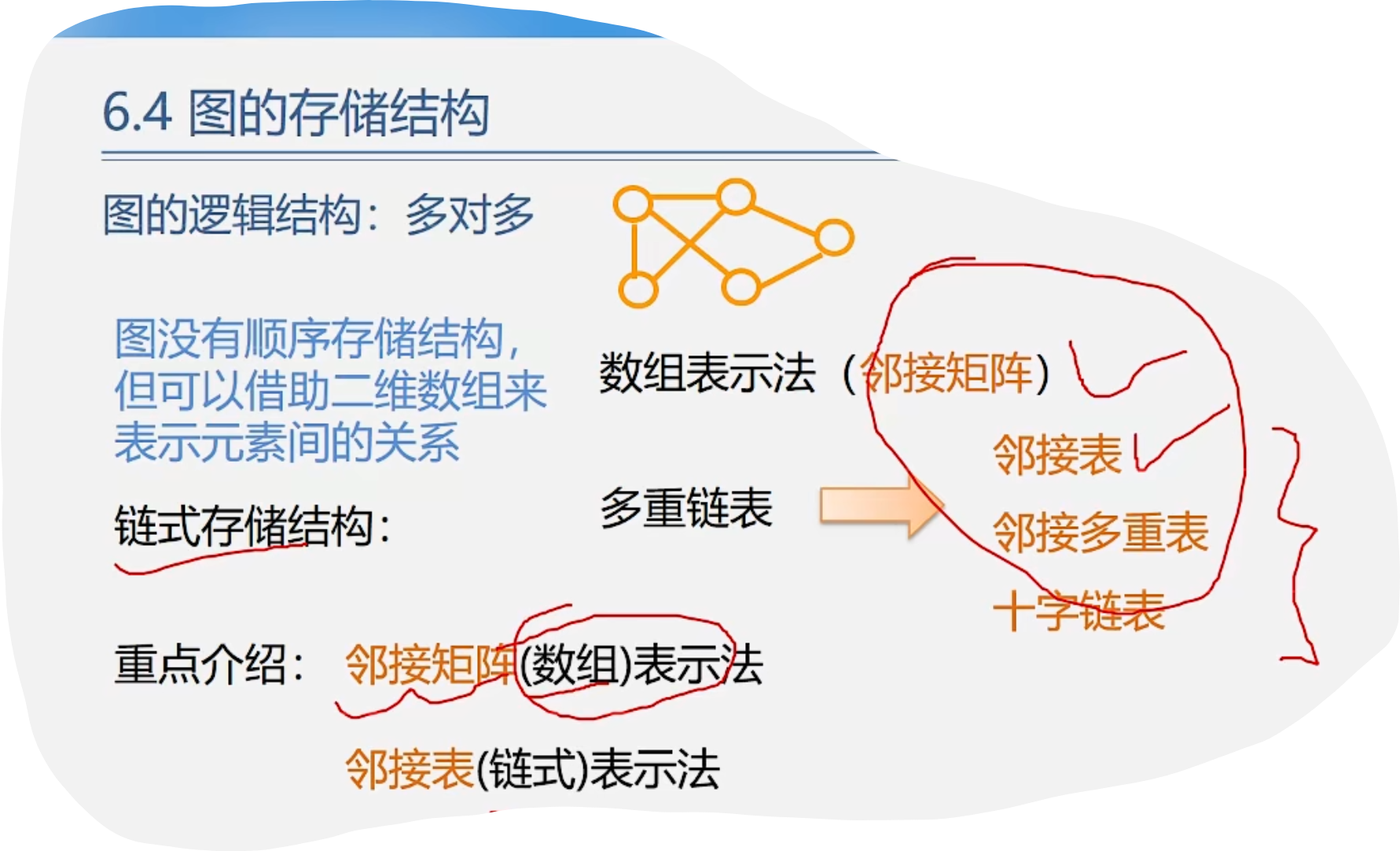
4.图的存储结构 

1.邻接矩阵 

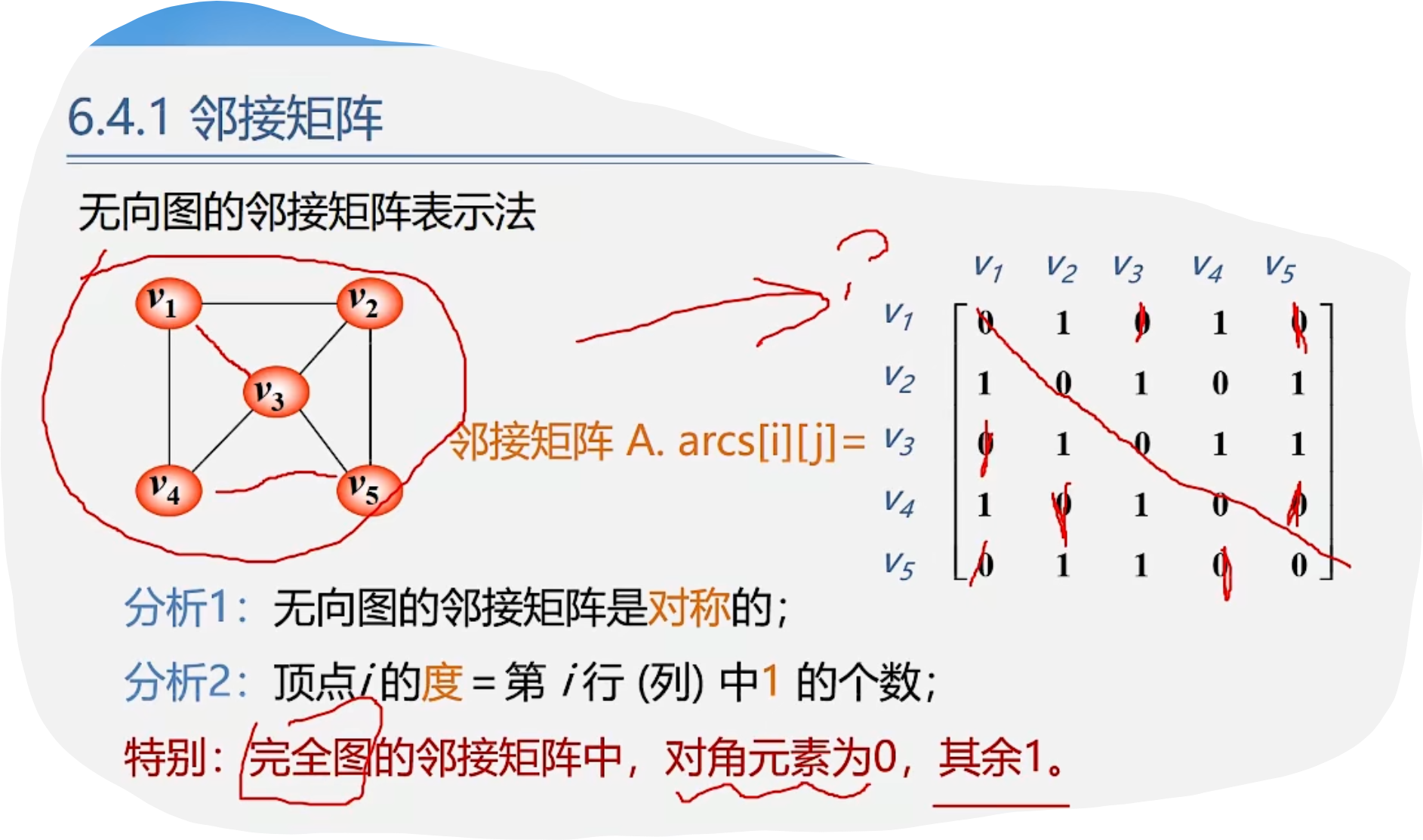
1.无向图的邻接矩阵表示法 

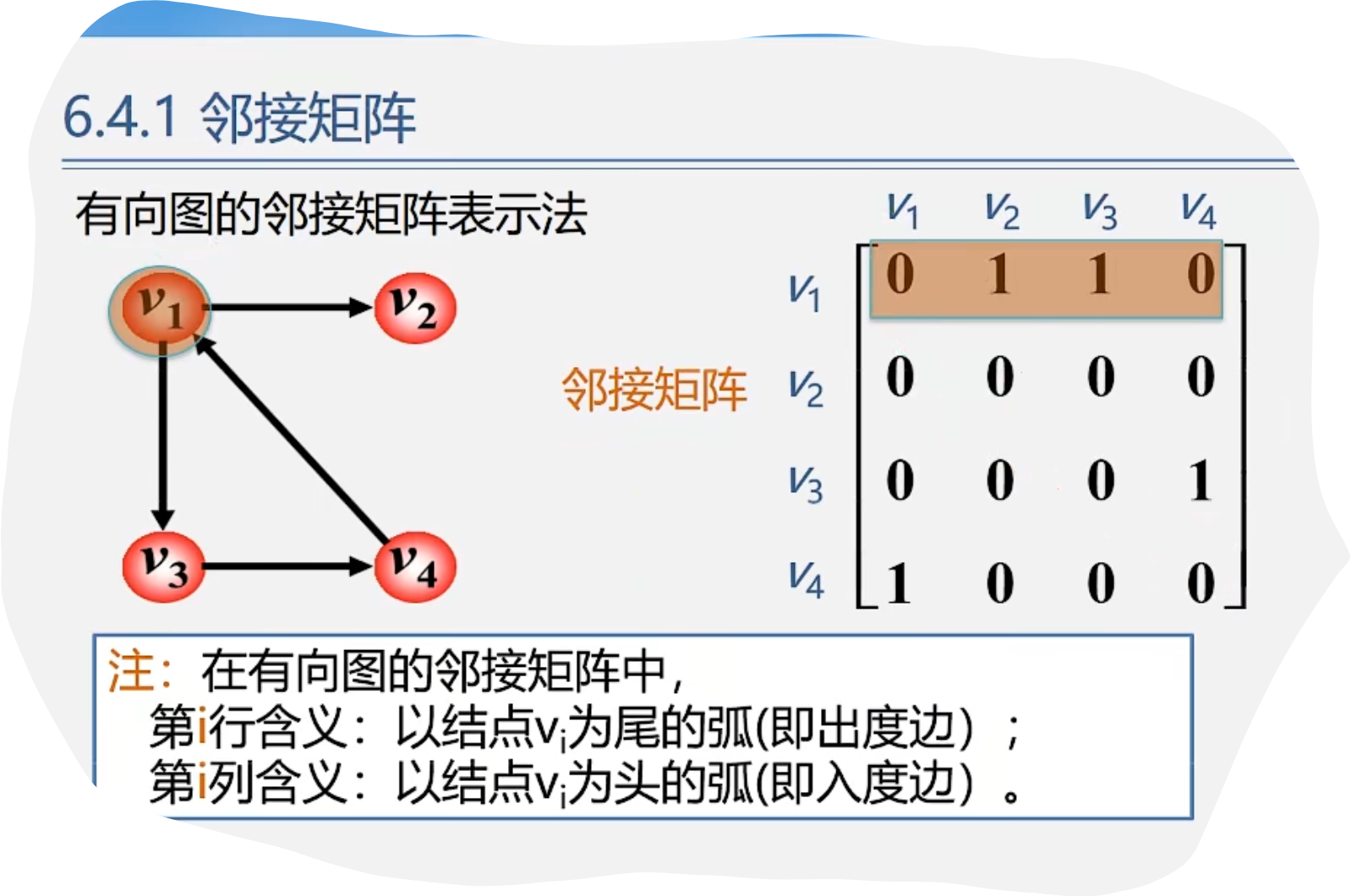
2.有向图的邻接矩阵表示法

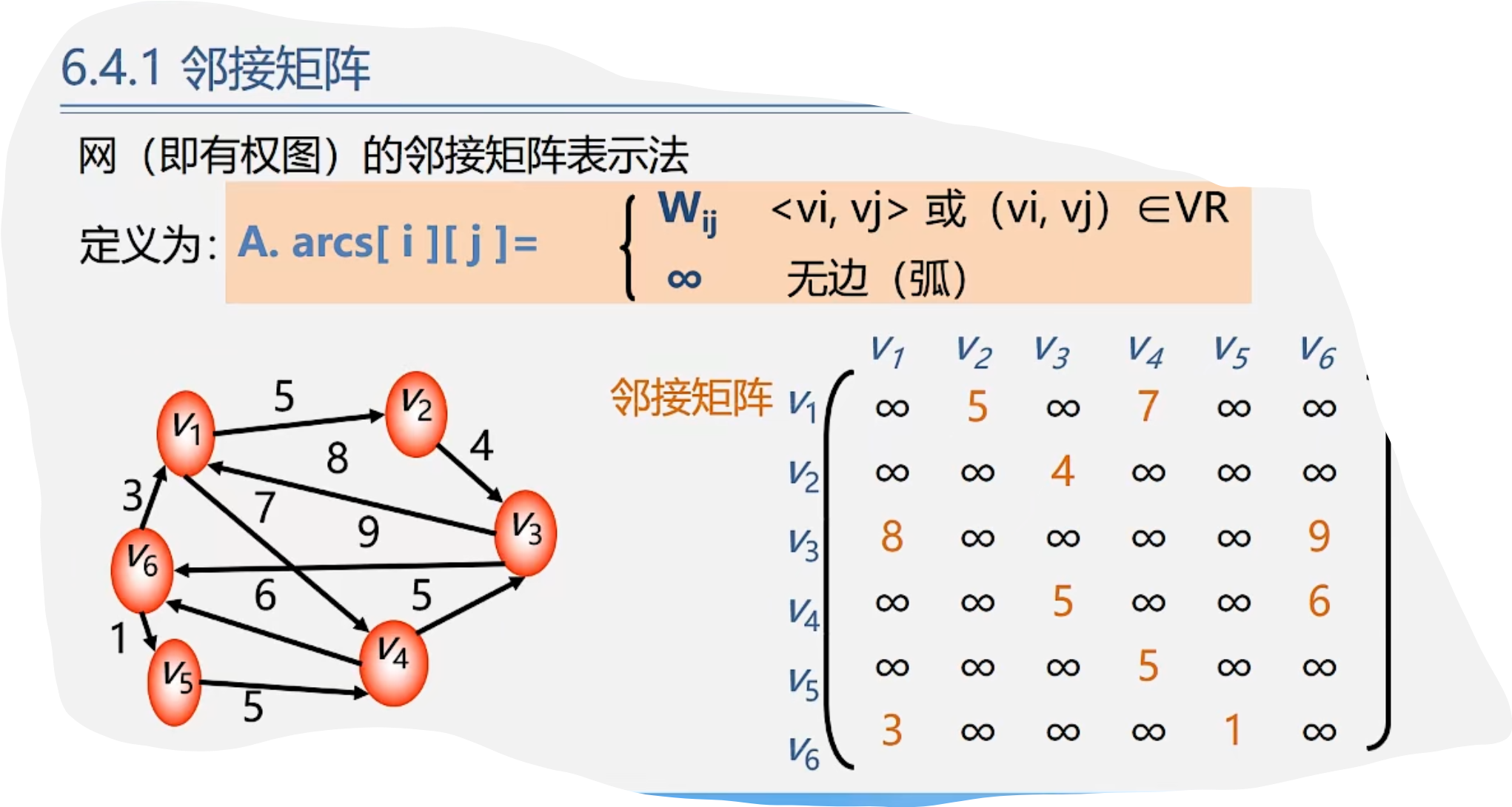
3.网（有权图）的邻接矩阵表示法 

代码示例：

 2.采用邻接矩阵表示法创建无向图

代码示例：

3.邻接表

1. 邻接表表示法（链式）

练习 

2.邻接表存储表示 

1.顶点的结点结构 

2.弧（边）的结点结构 

 3.图的结构定义

代码示例：

 3.邻接表操作举例

4.采用邻接表表示法创建无向网 

代码示例： 

5.邻接表特点 

 6.临界矩阵与邻接表表示法的关系

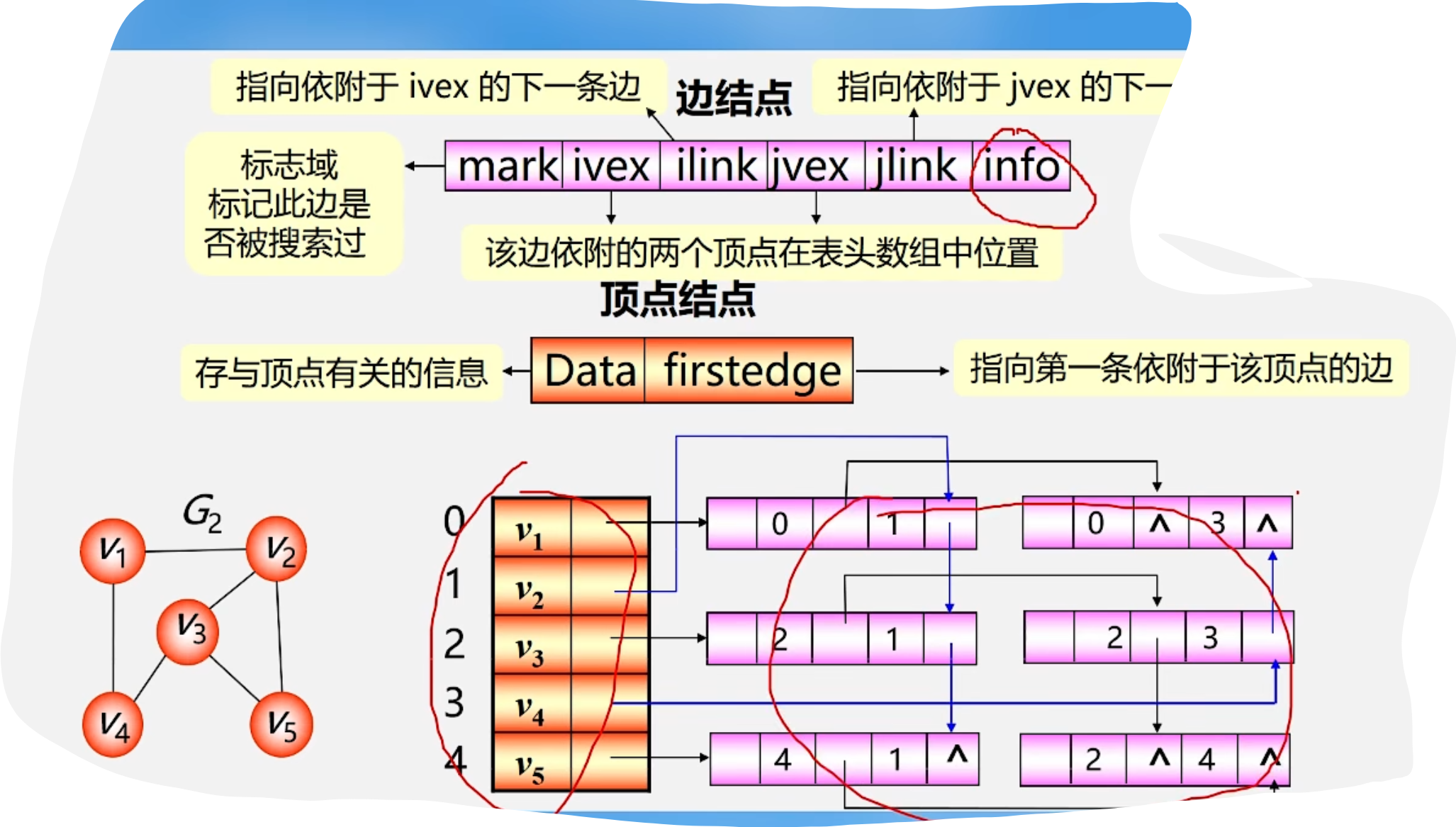
5.十字链表 （用于有向图）

6.邻接多重表 

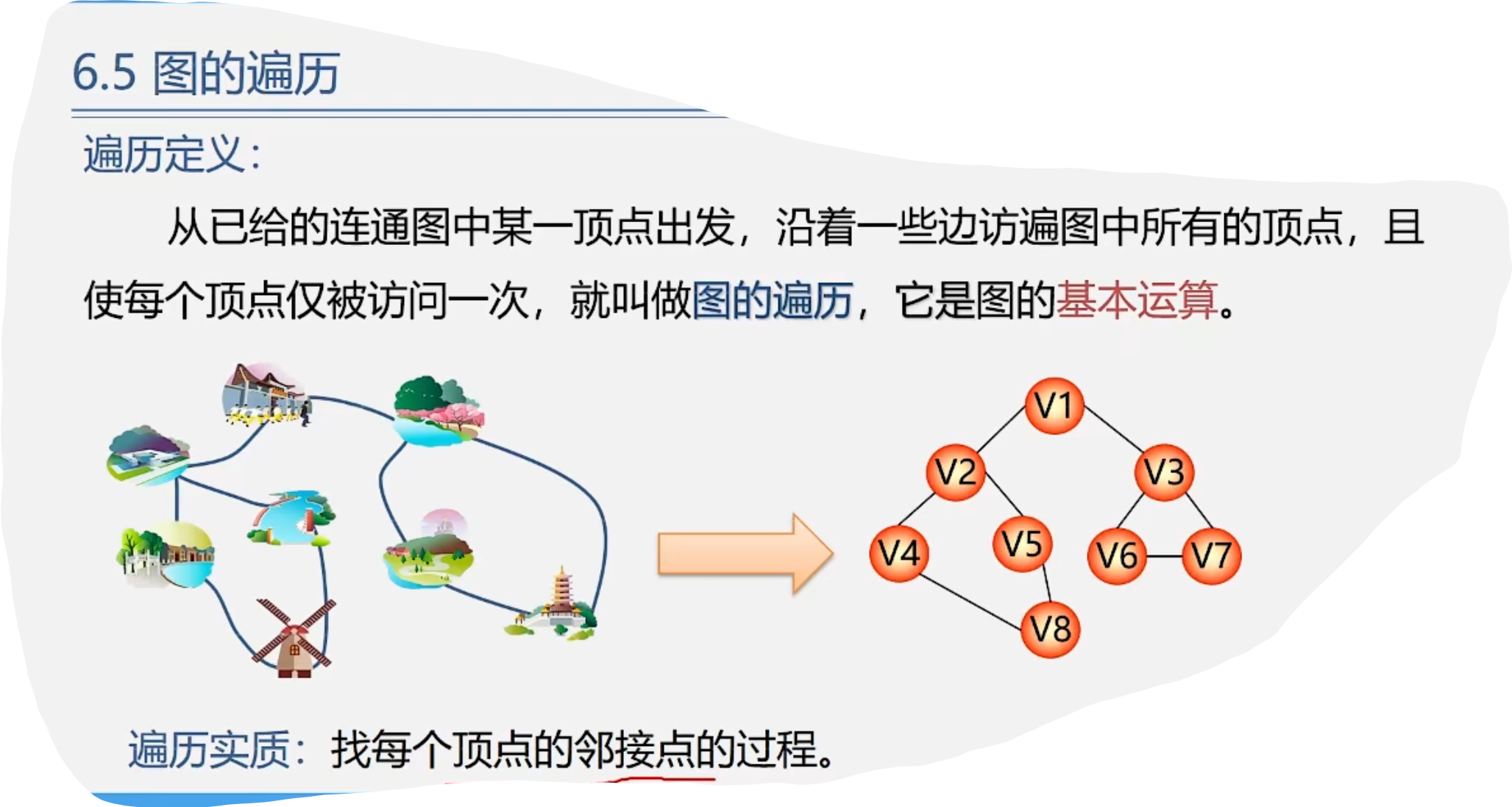
7.图的遍历 

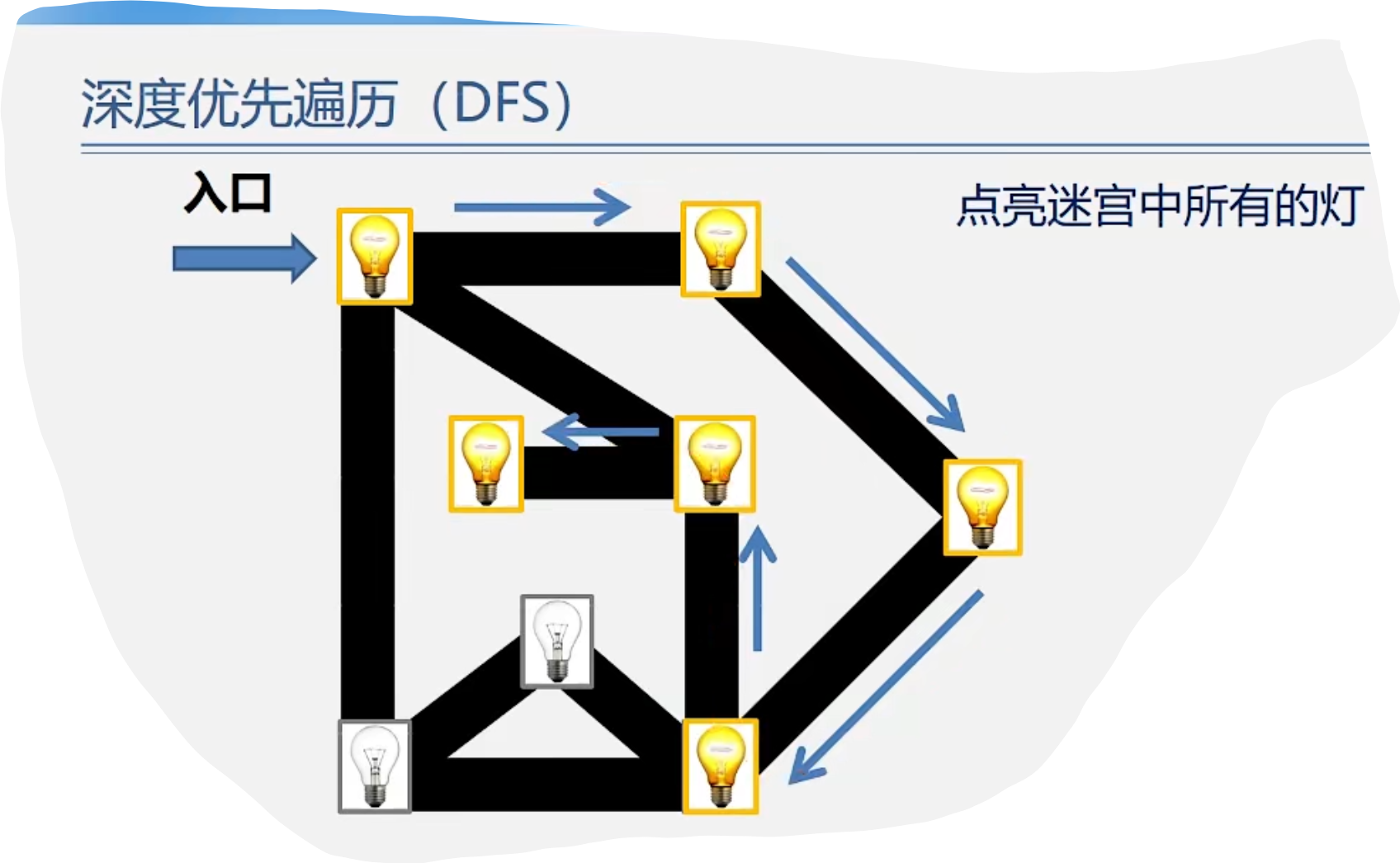
1.DFS 

代码示例：

 

2.BFS 

代码示例：

 

8.总的代码

 

---

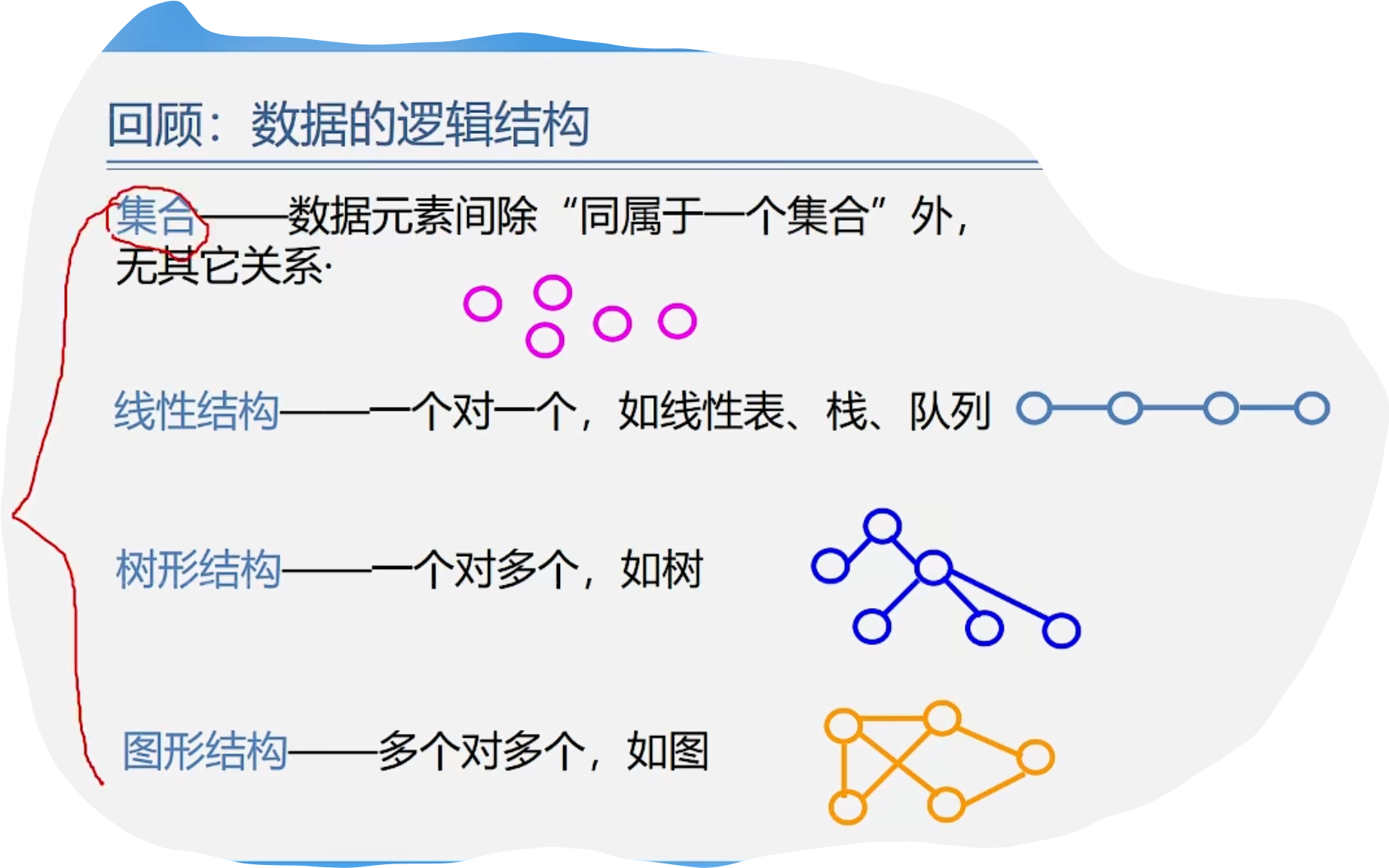
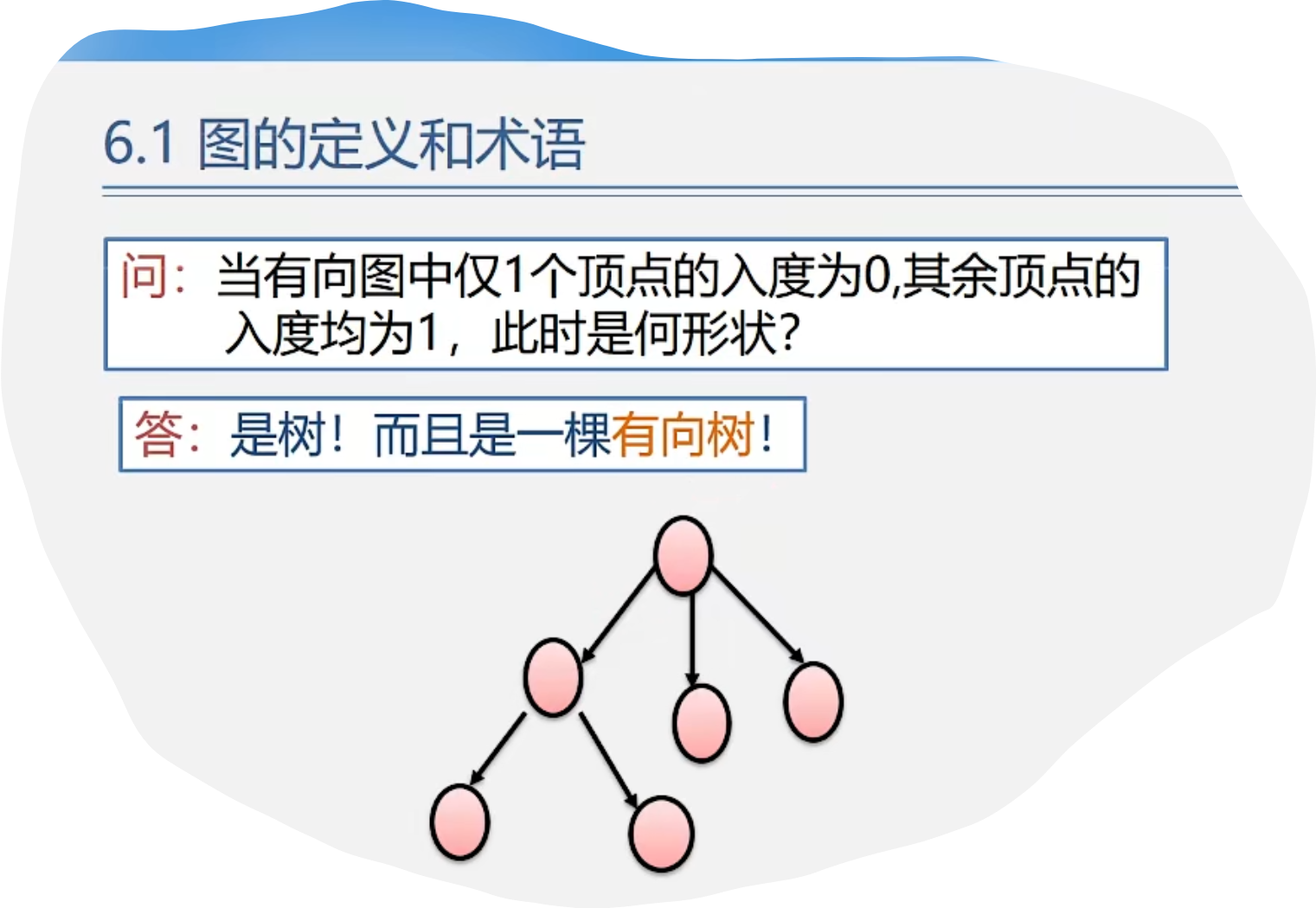
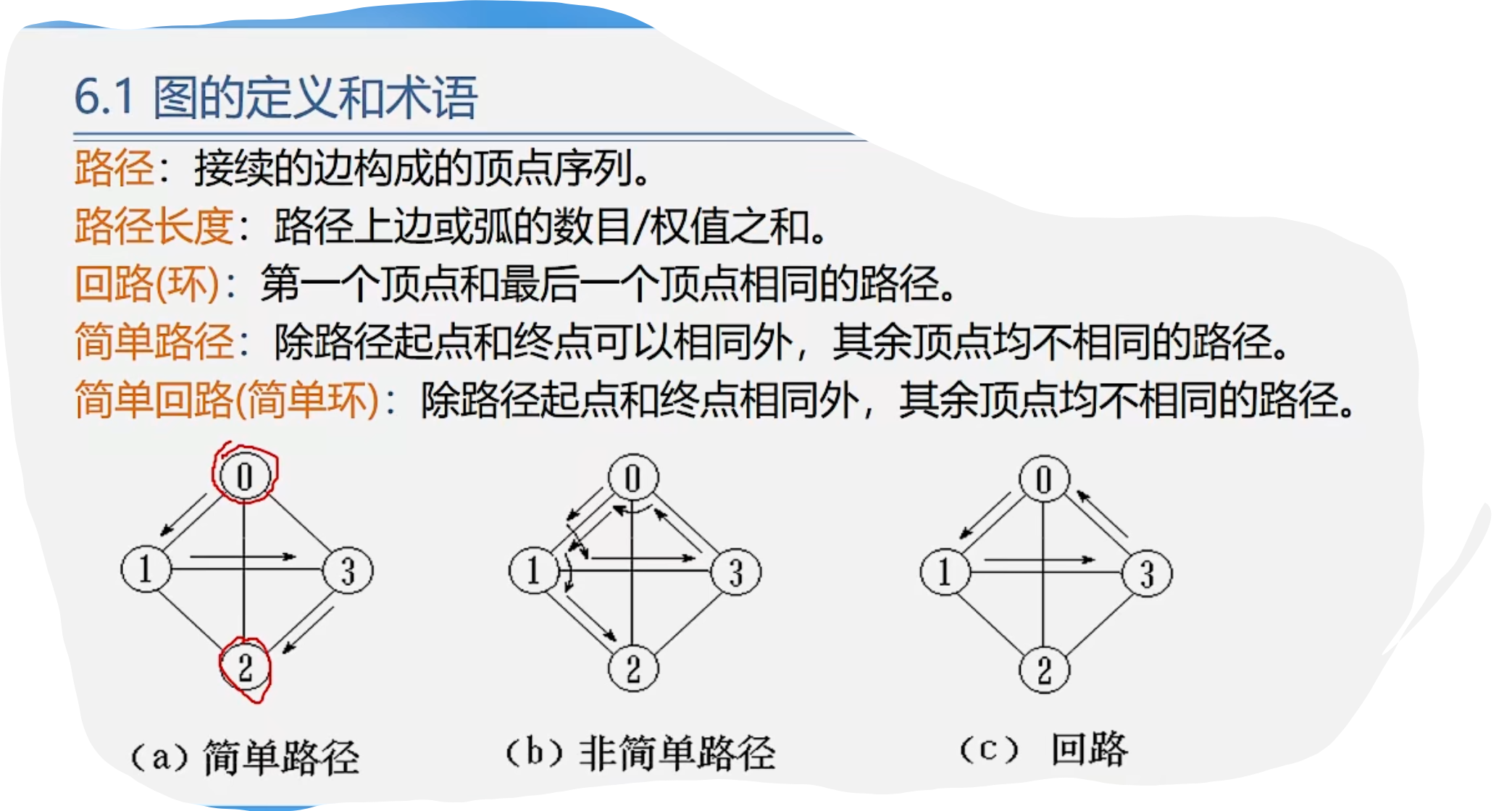
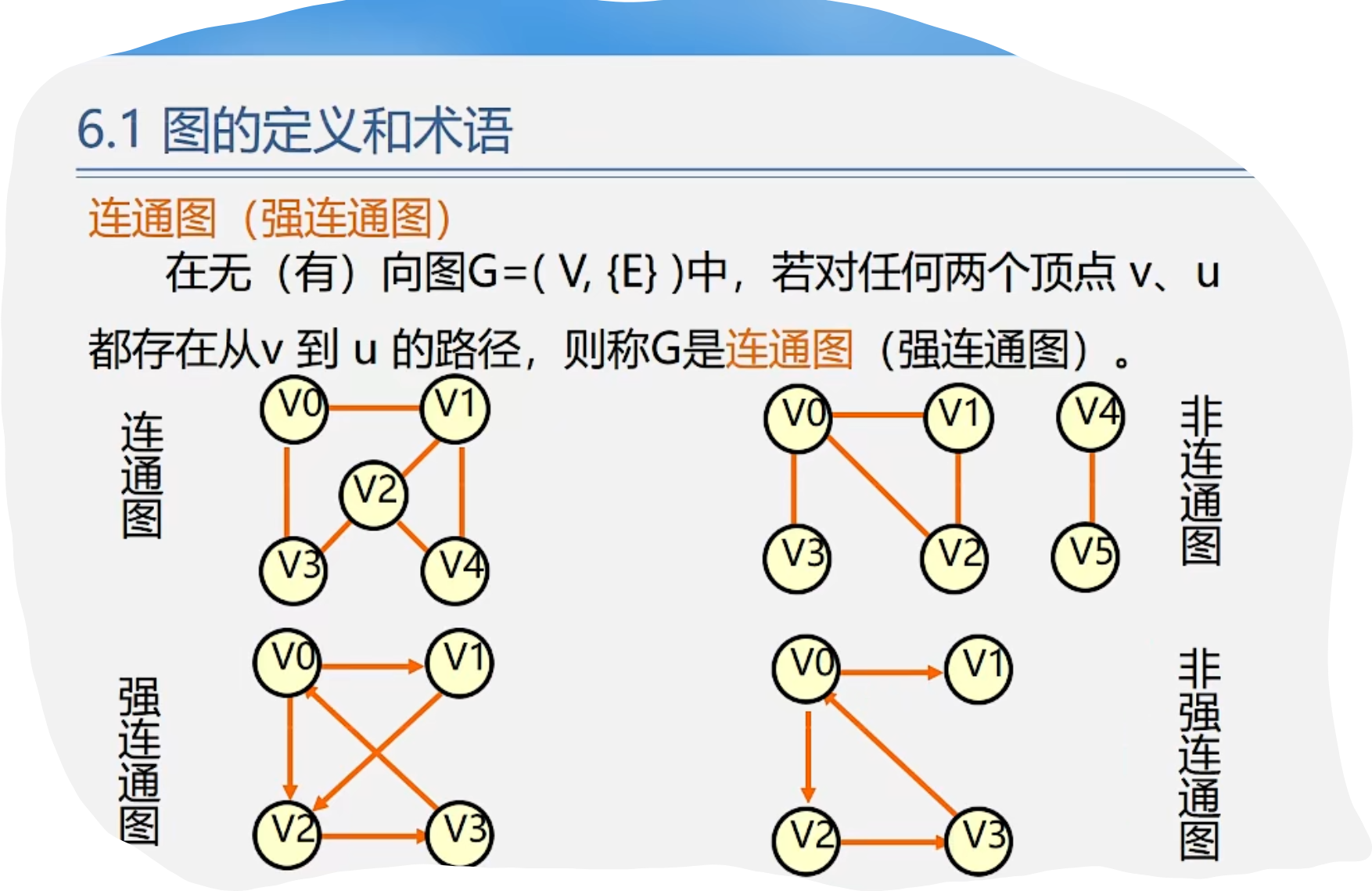
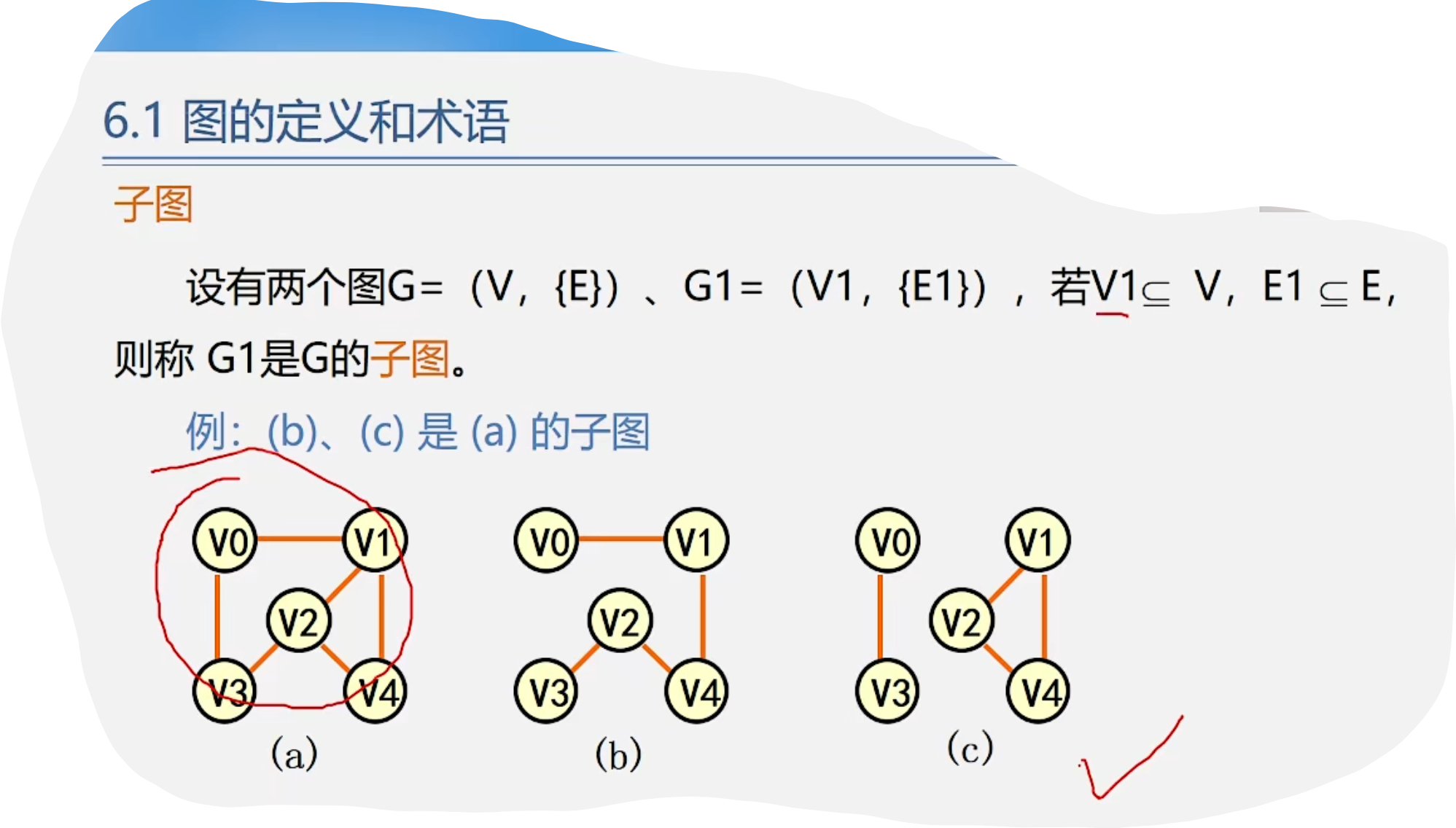
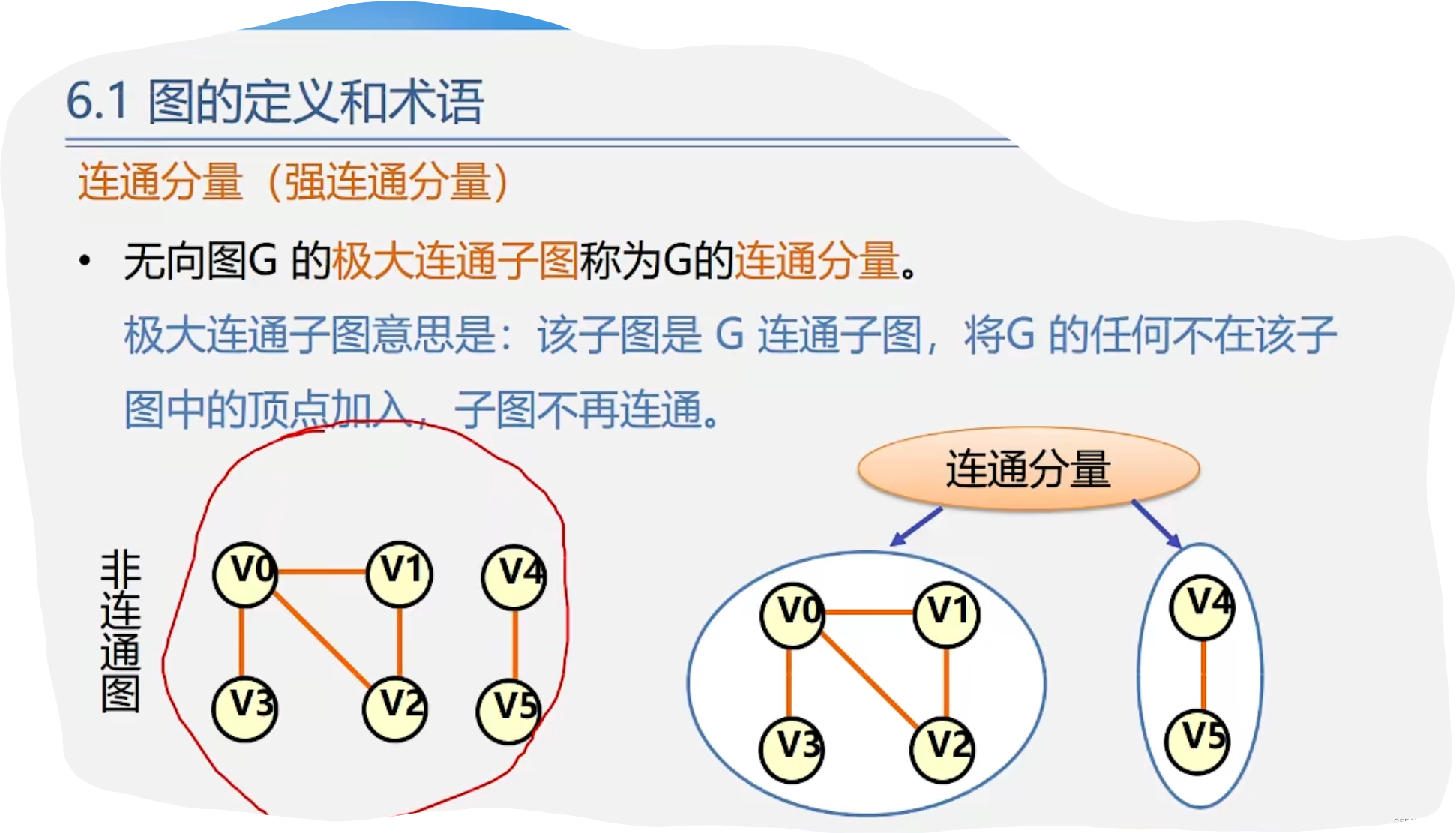
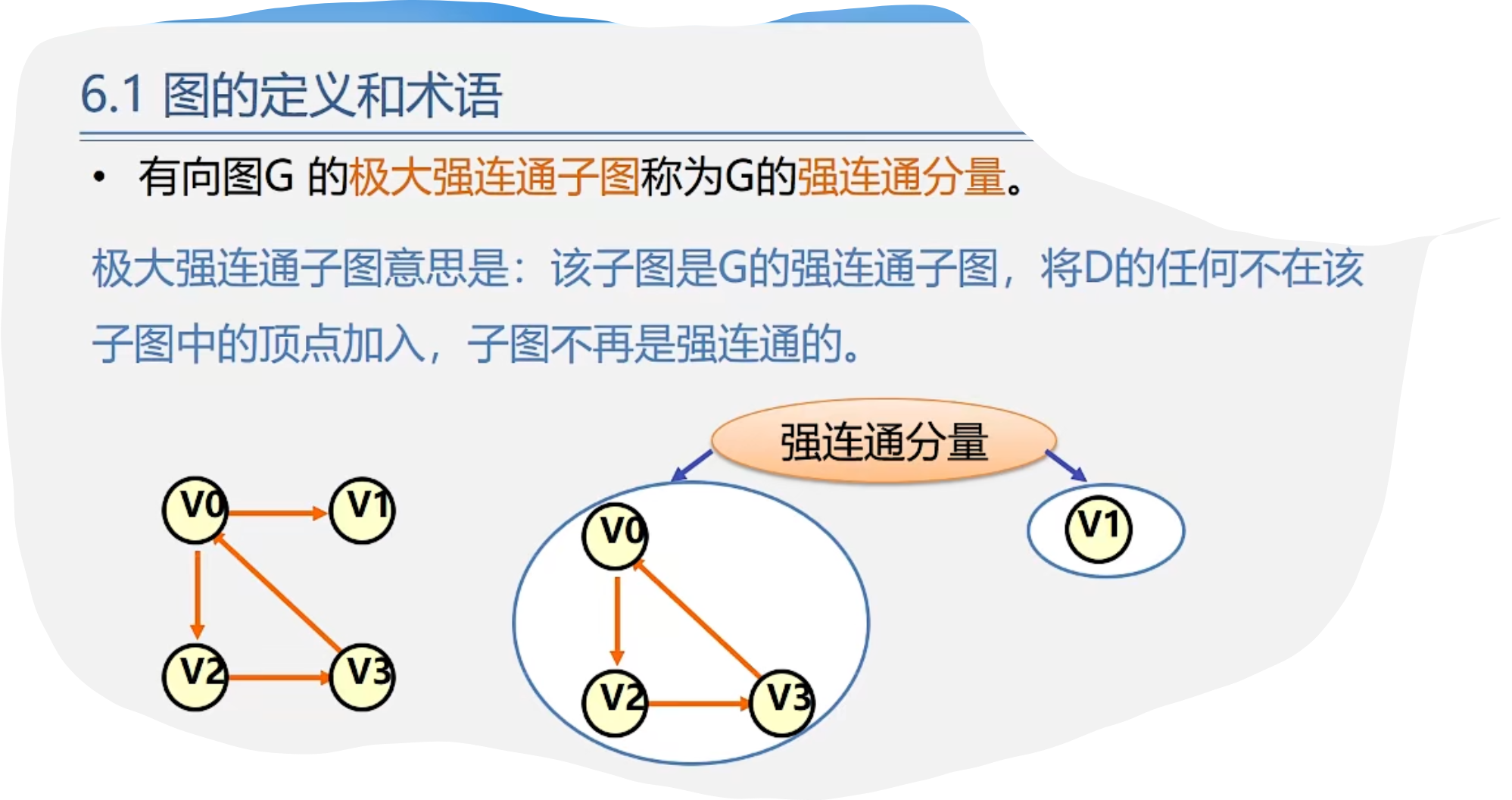
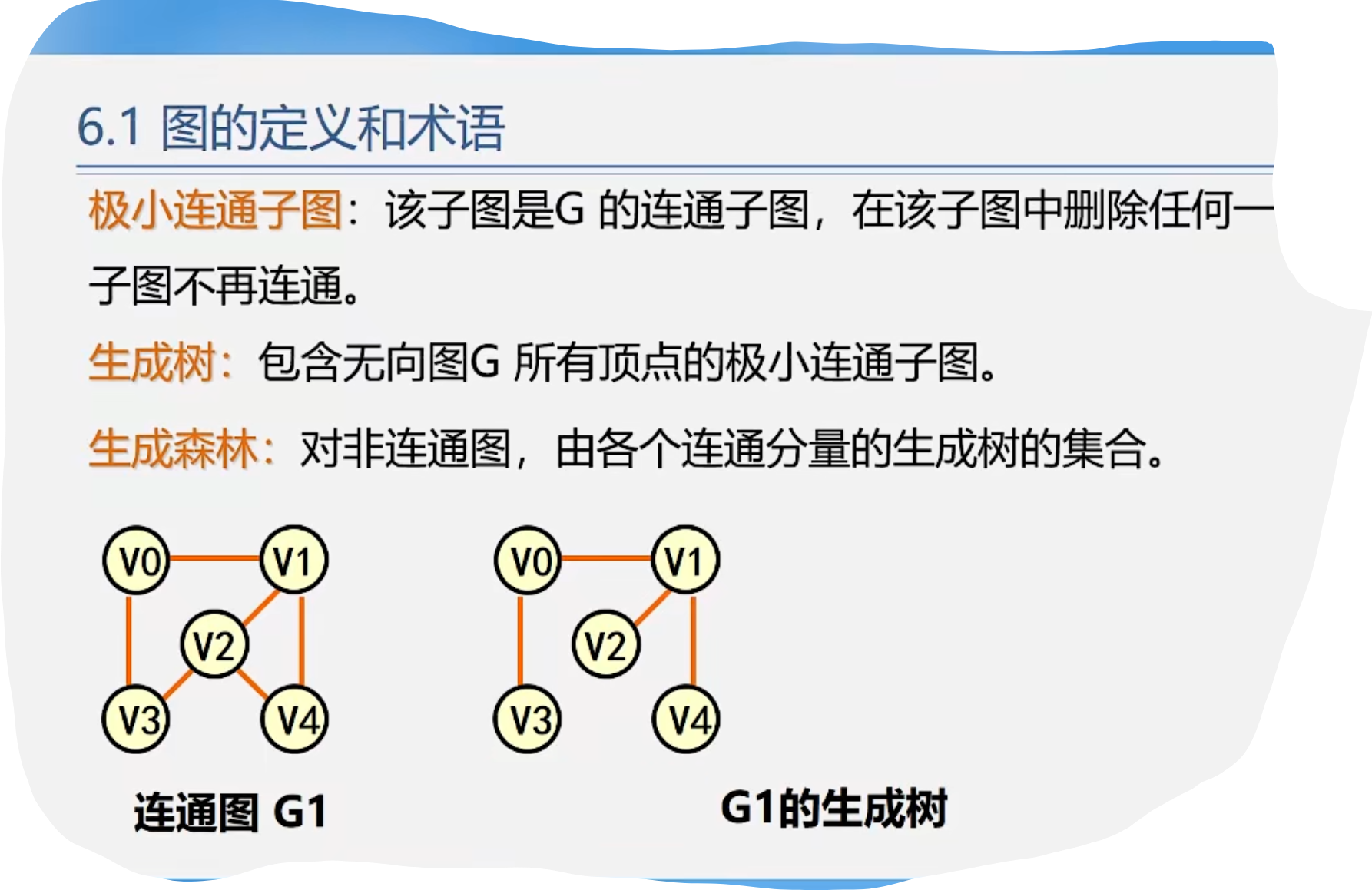
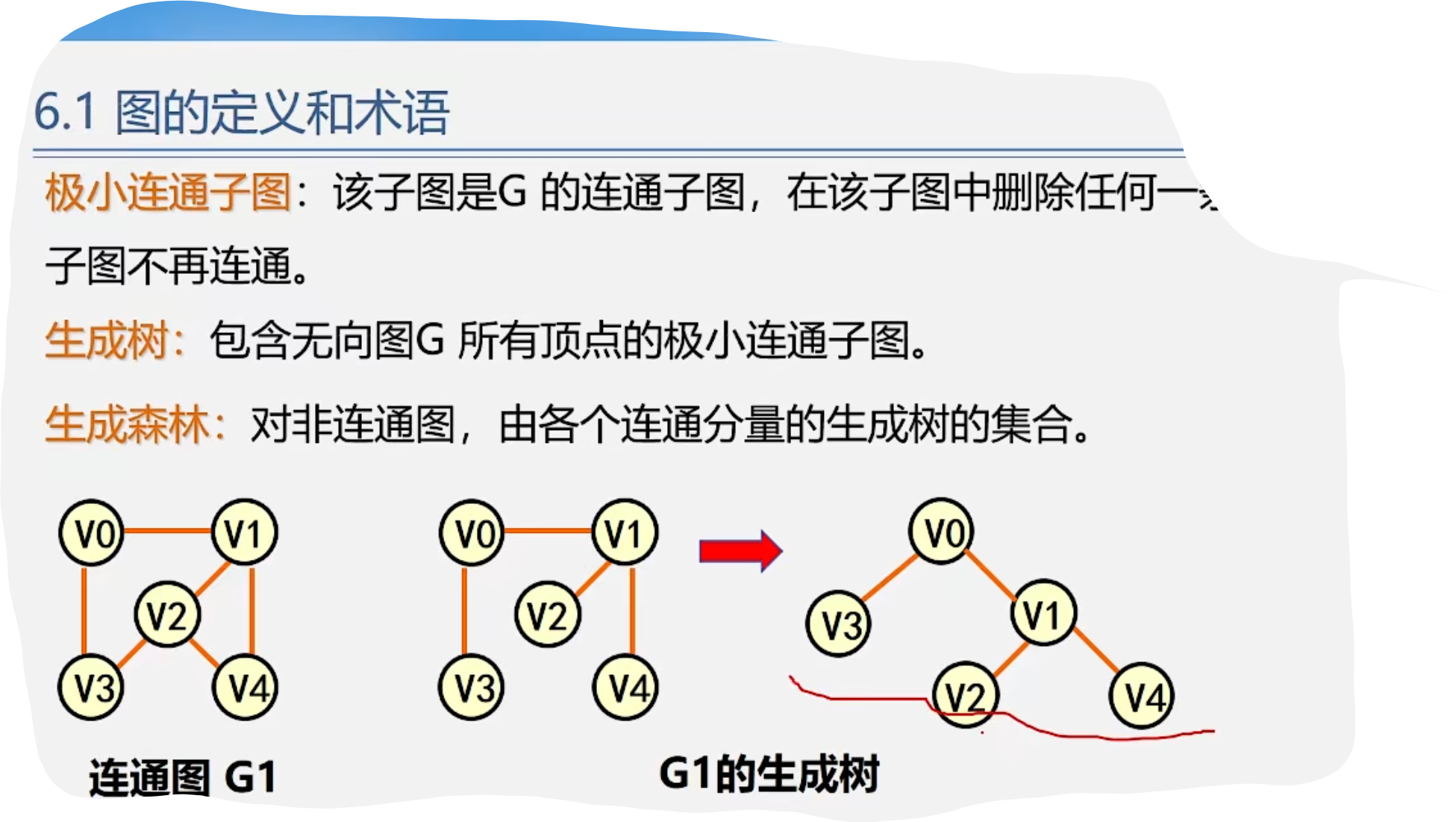
 1.图的定义和术语

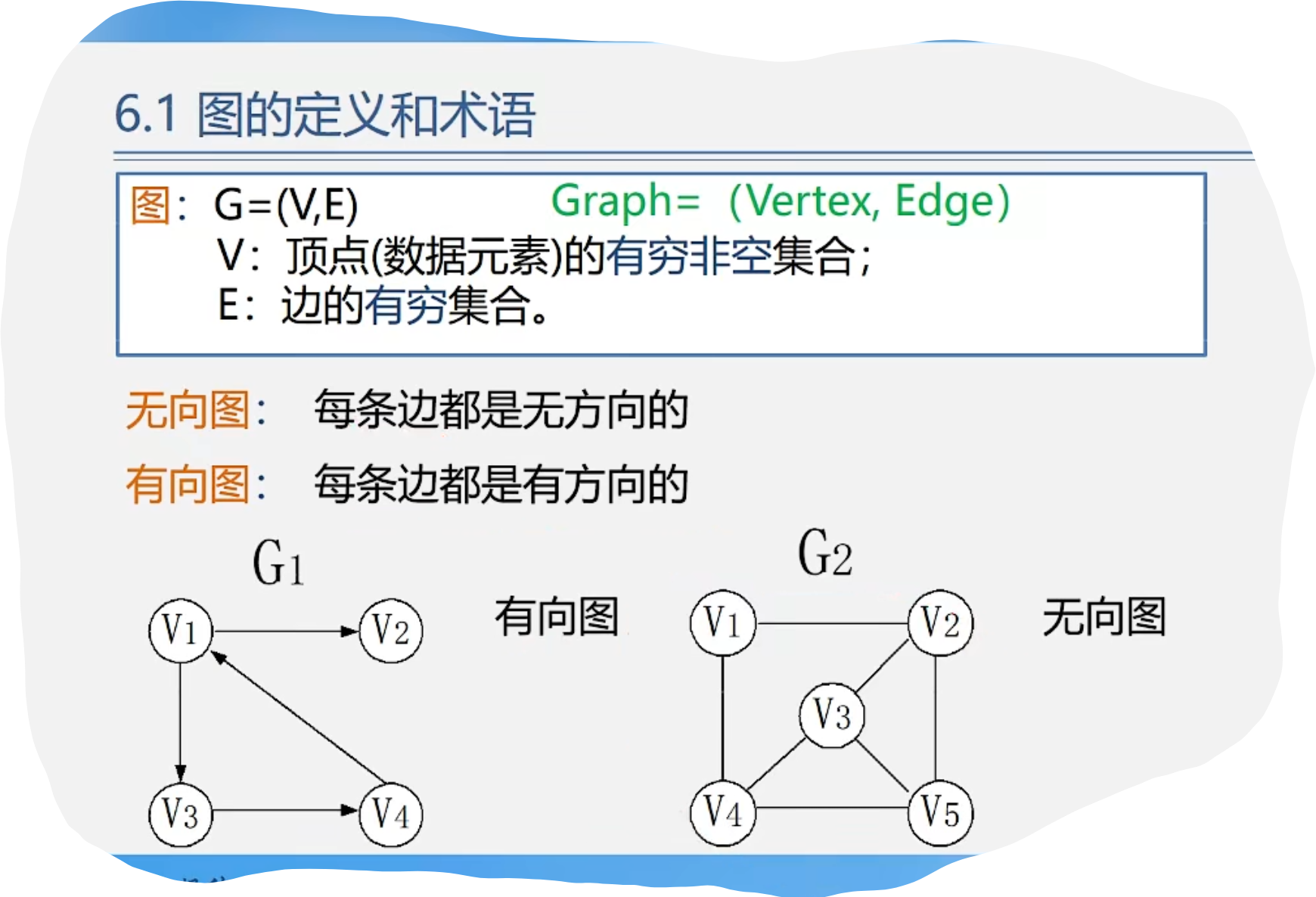
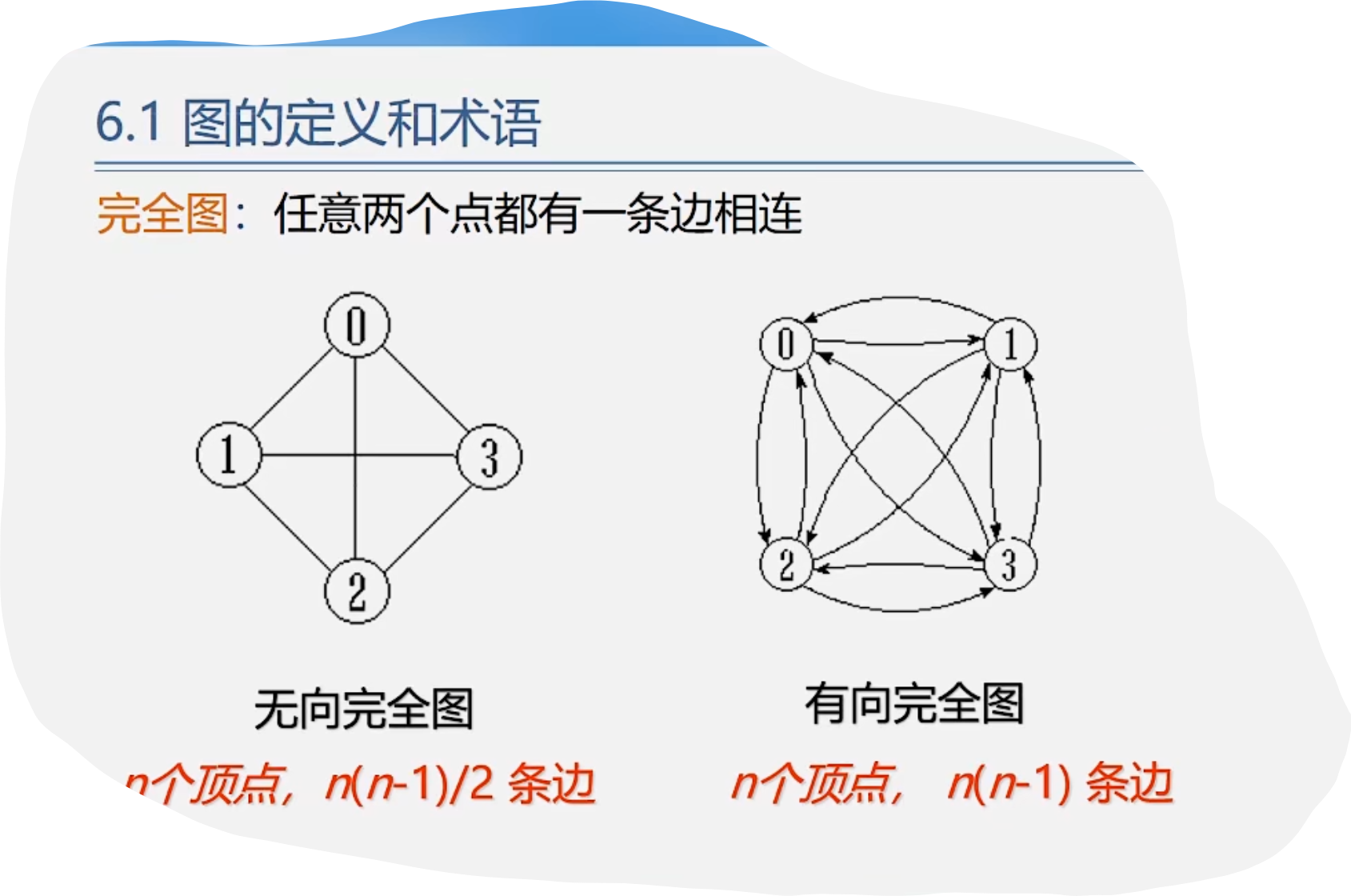
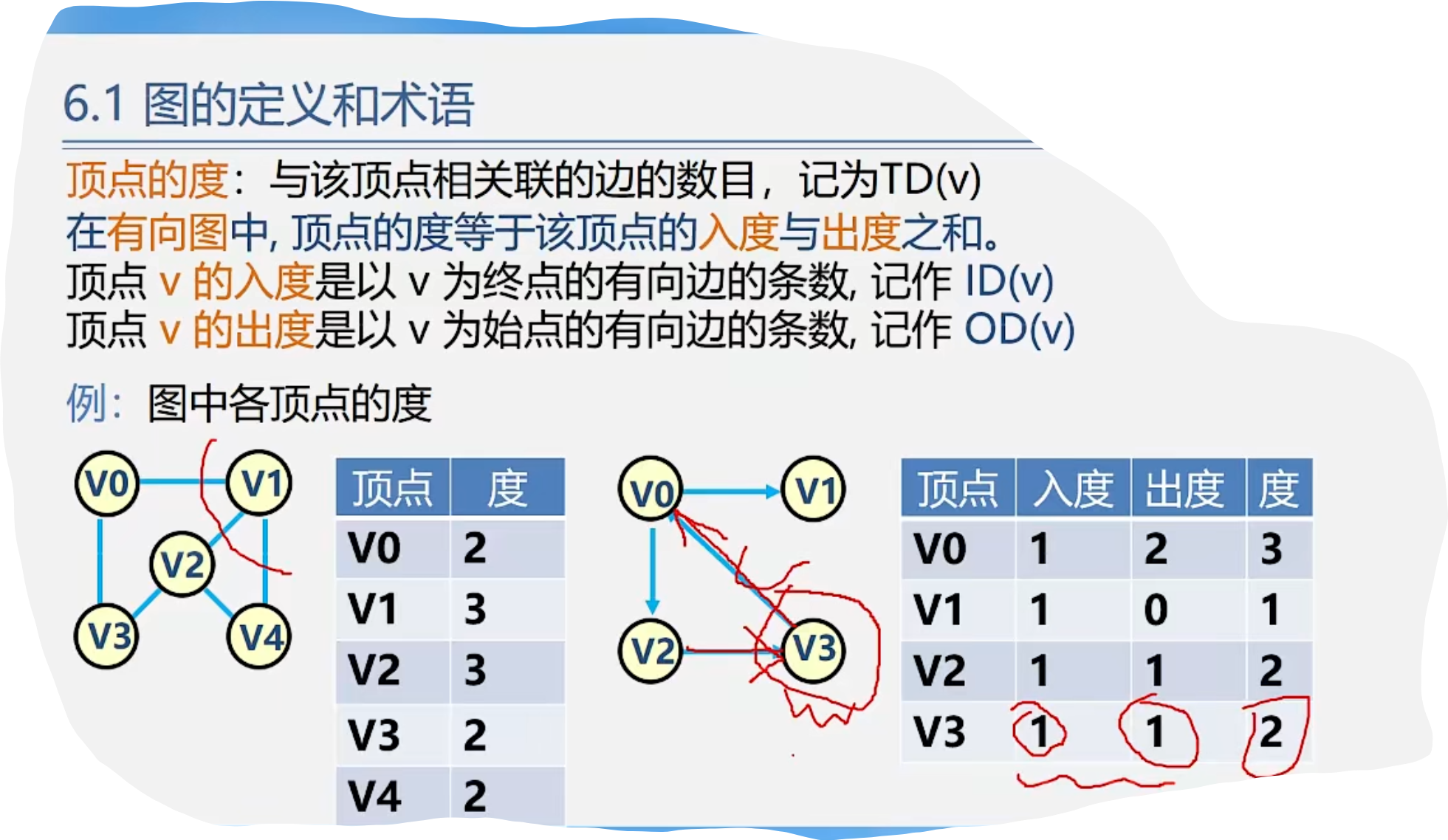
2.案例引入 

1.六度空间理论

3.图的类型定义 

4.图的存储结构 

1.邻接矩阵 

1.无向图的邻接矩阵表示法 

2.有向图的邻接矩阵表示法

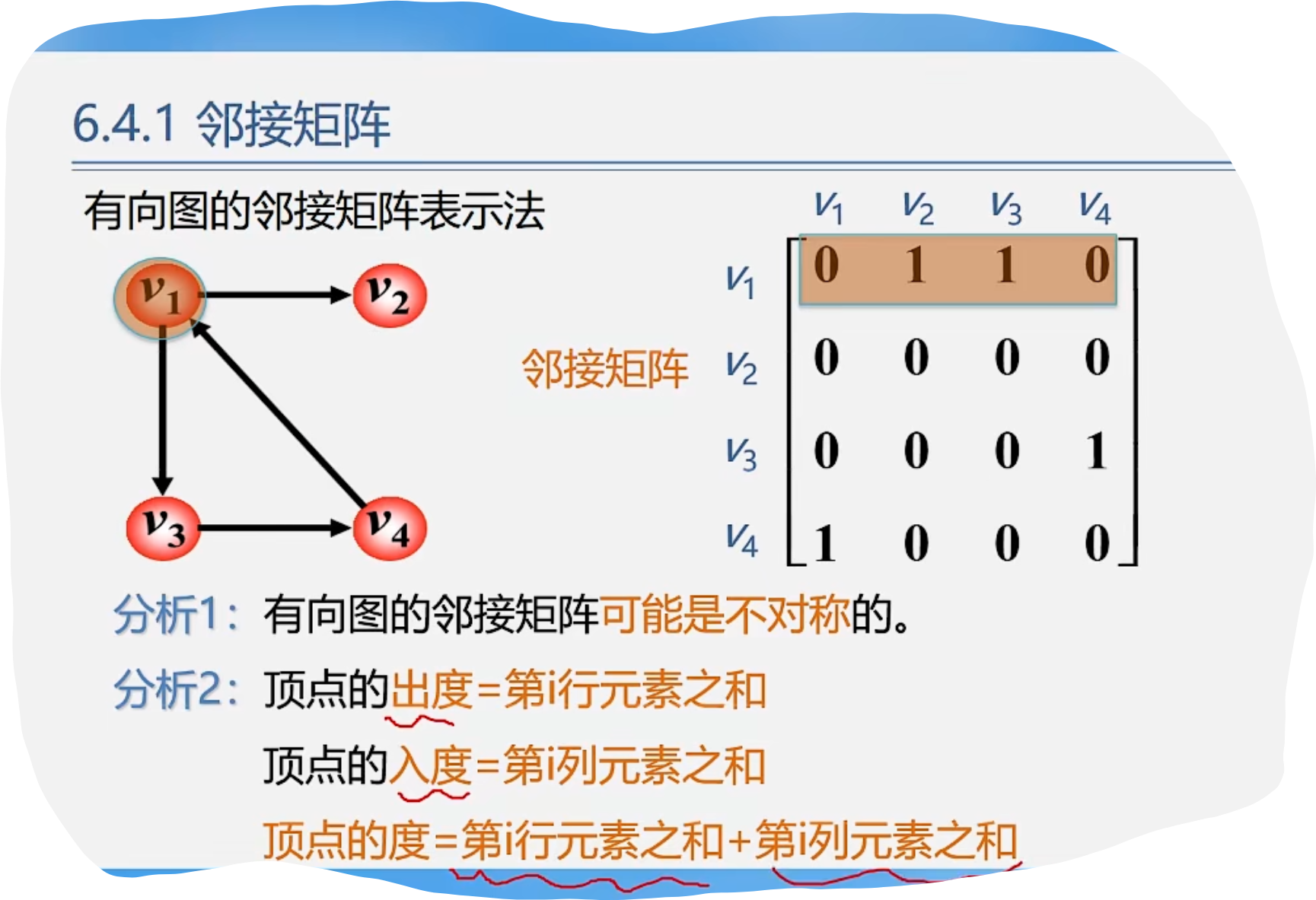
3.网（有权图）的邻接矩阵表示法 

代码示例：

typedef struct{char vexs[100];int arcs[32767][32767];int vexnum,arcnum;
}amgraph;

 2.采用邻接矩阵表示法创建无向图

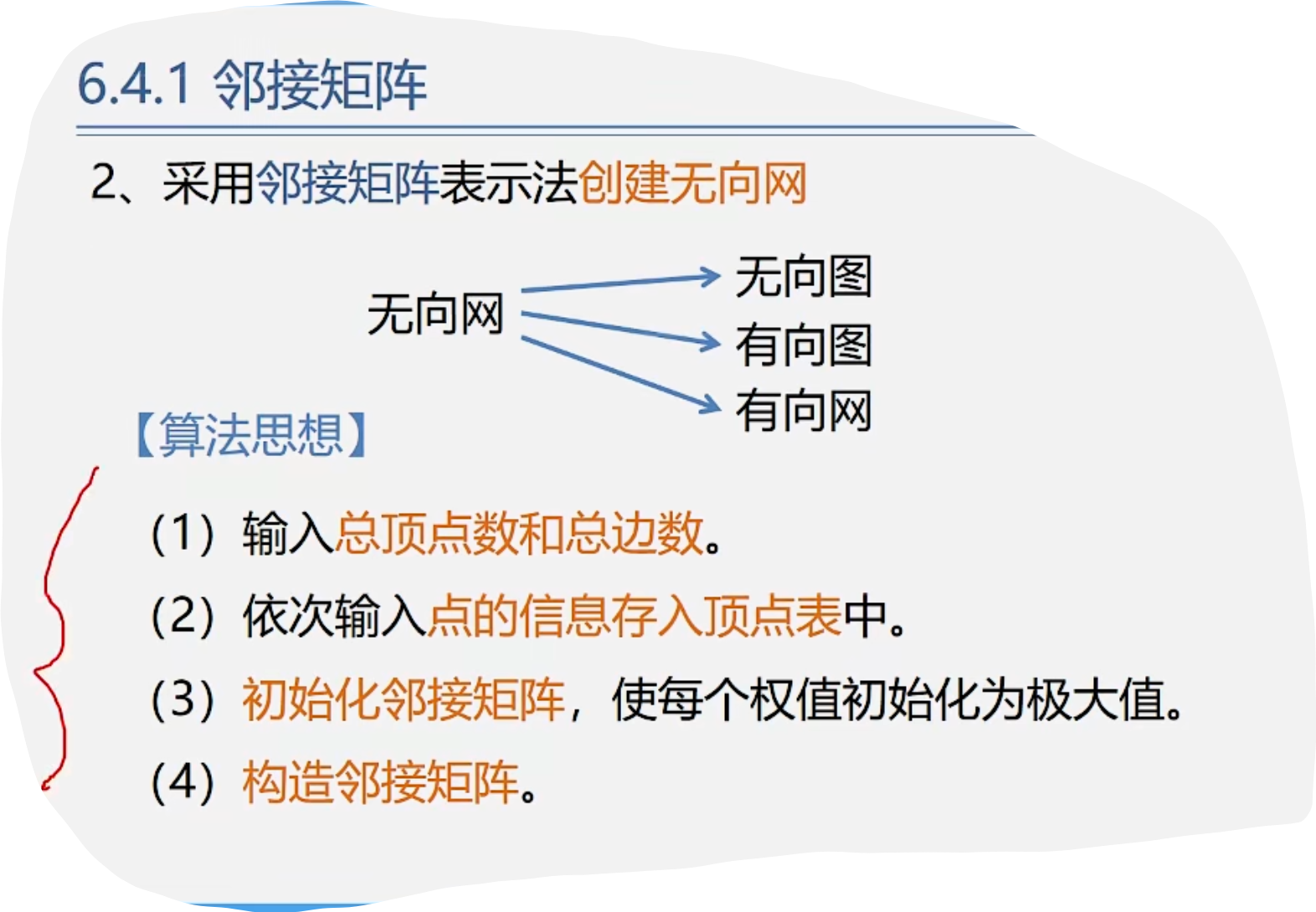
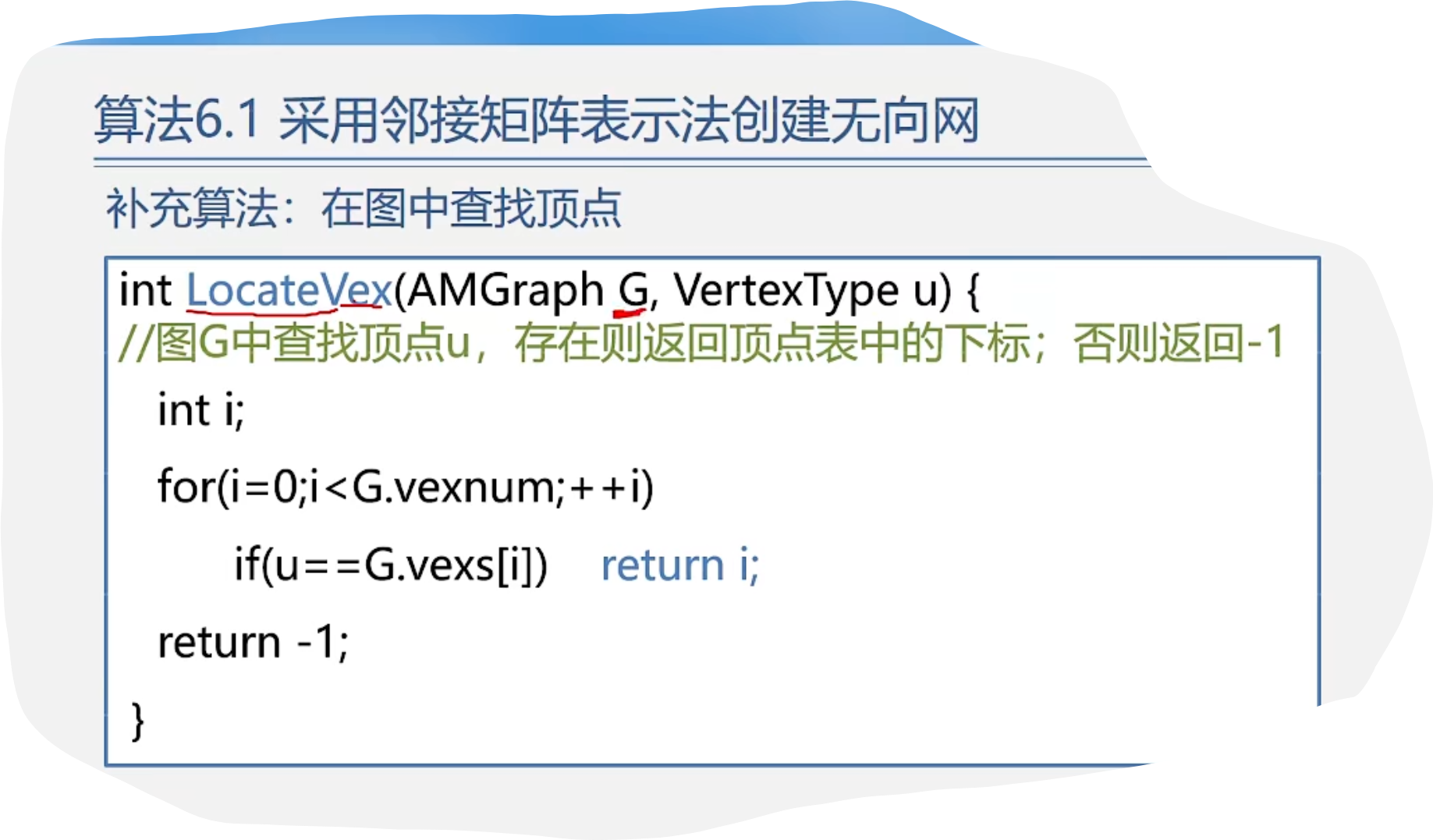
代码示例：

int locatevex(amgraph &g,char u)
{for(int i = 0; i < g.vexnum; i++){if(u == g.vexs[i]) return i;}return -1;
}int createudn(amgraph &g)
{cin >> g.vexnum >> g.arcnum;for(int i = 0; i < g.vexnum; i++){cin >> g.vexs[i];}for(int i = 0; i < g.arcnum; i++)for(int j = 0; j < g.arcnum; j++)g.arcs[i][j] = 32767;for(int k = 0; k < g.arcnum; k++){char v1,v2;int w;cin >> v1 >> v2 >> w;int i = locatevex(g,v1);int j = locatevex(g,v2);g.arcs[i][j] = w;g.arcs[j][i] = w;}return 1;
}

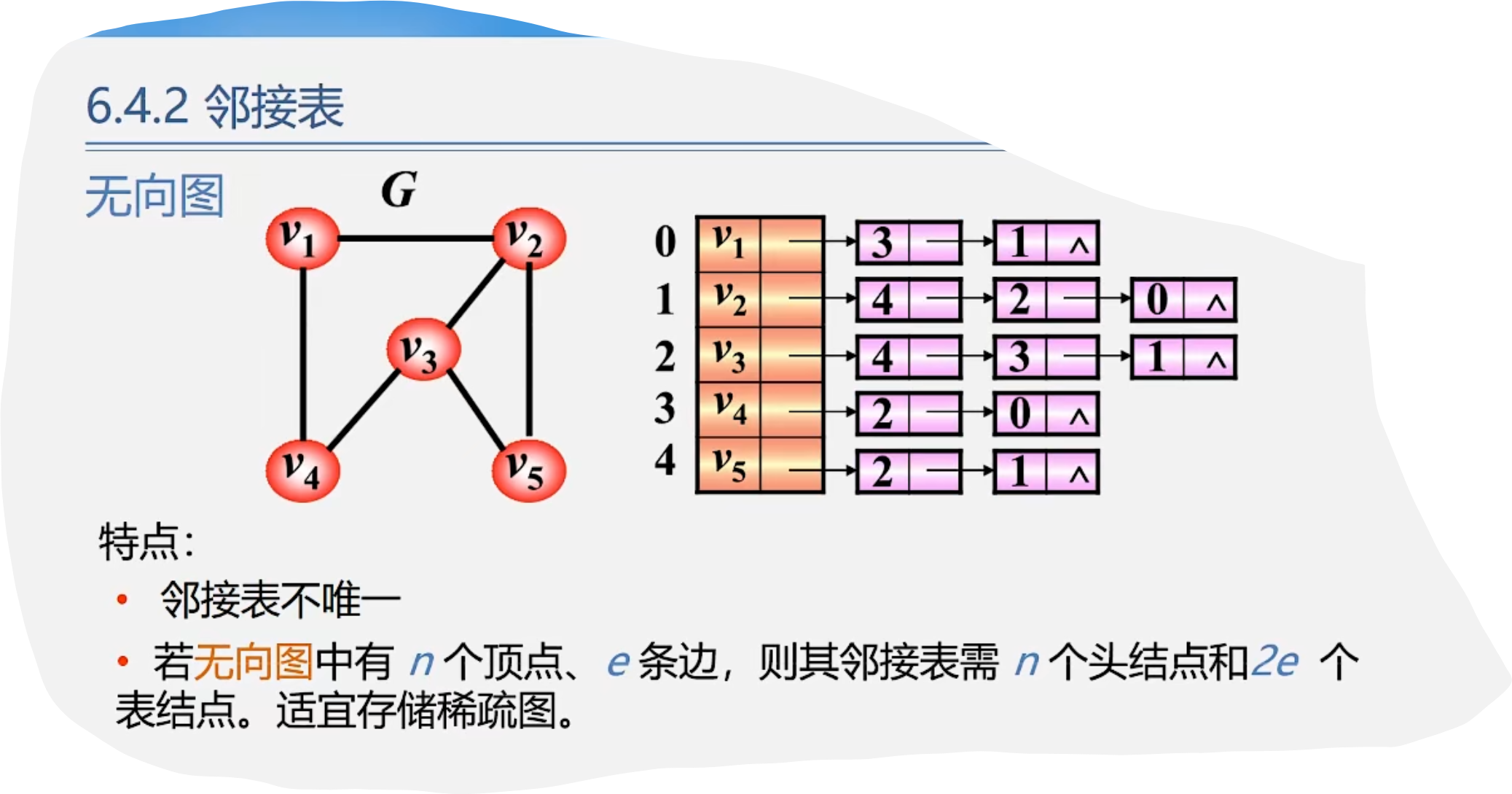
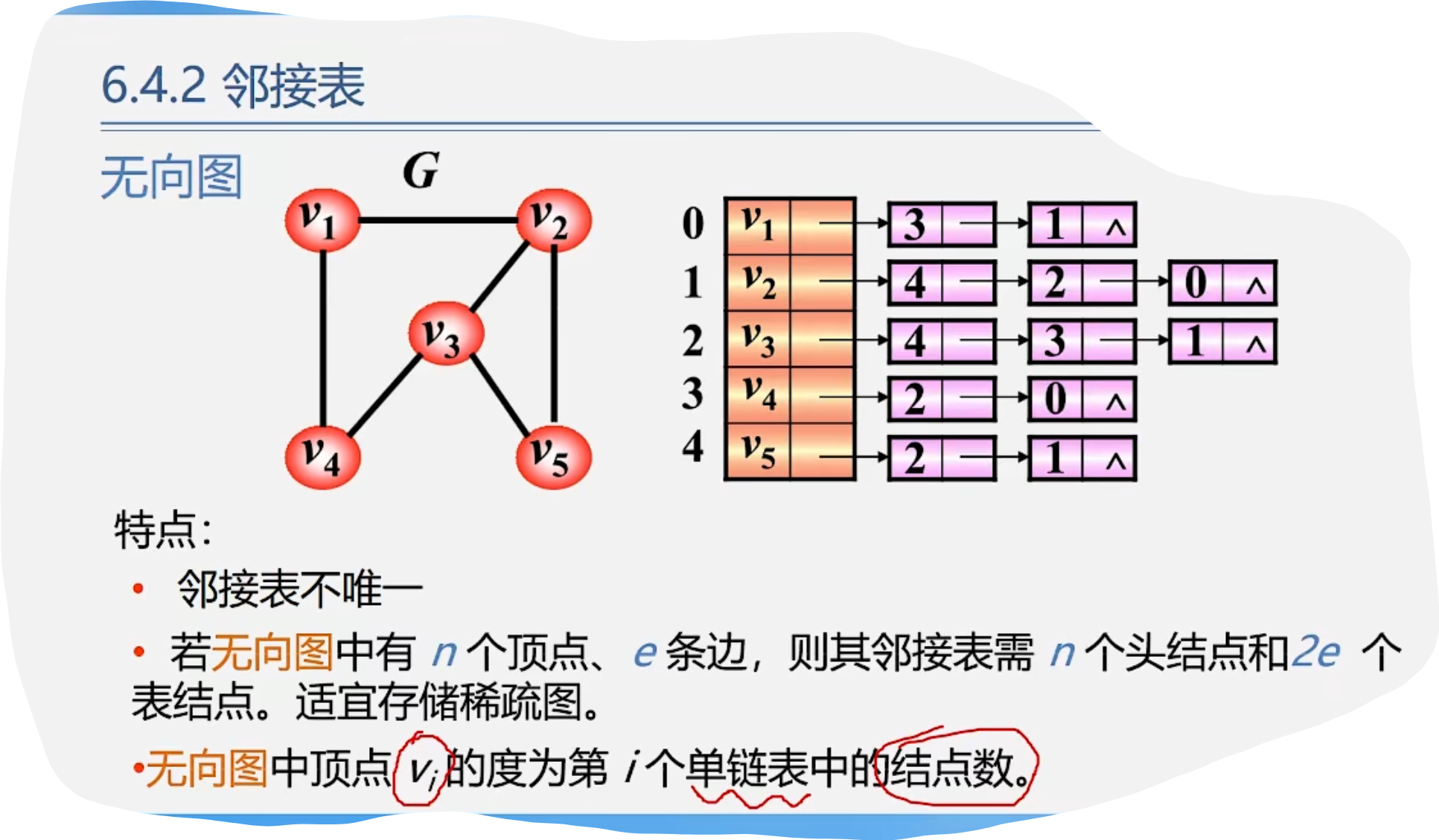
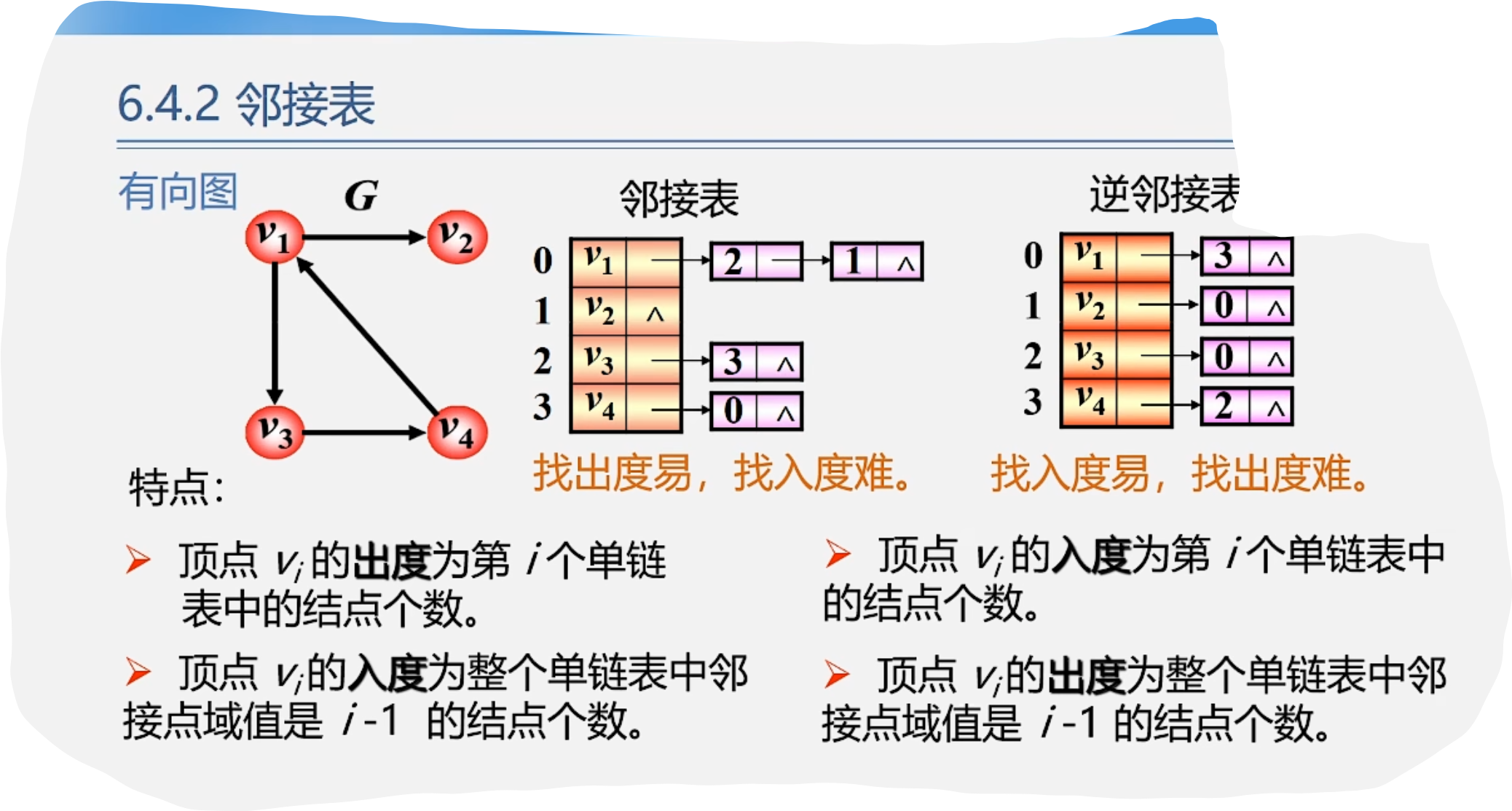
3.邻接表

1. 邻接表表示法（链式）

 

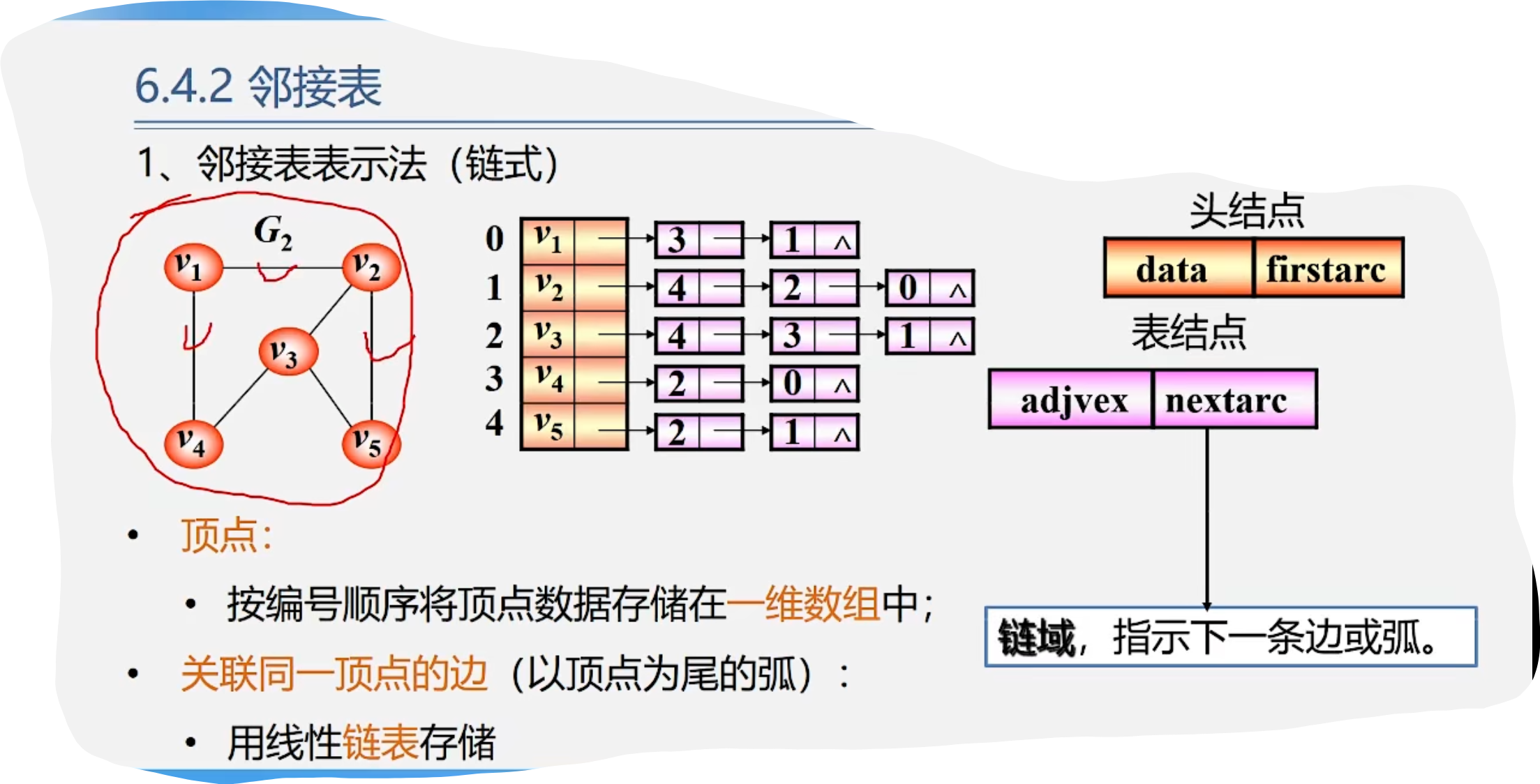
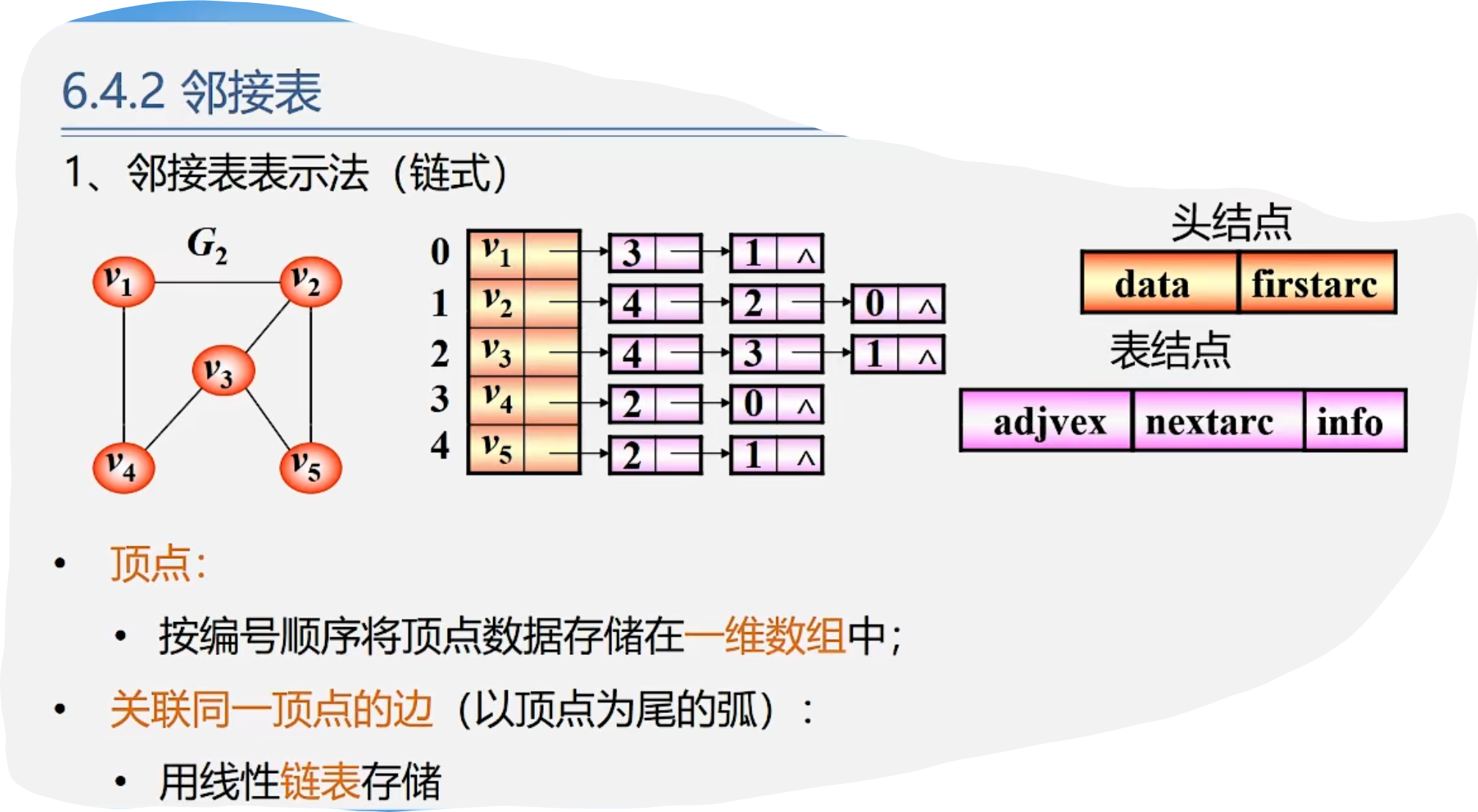
练习 

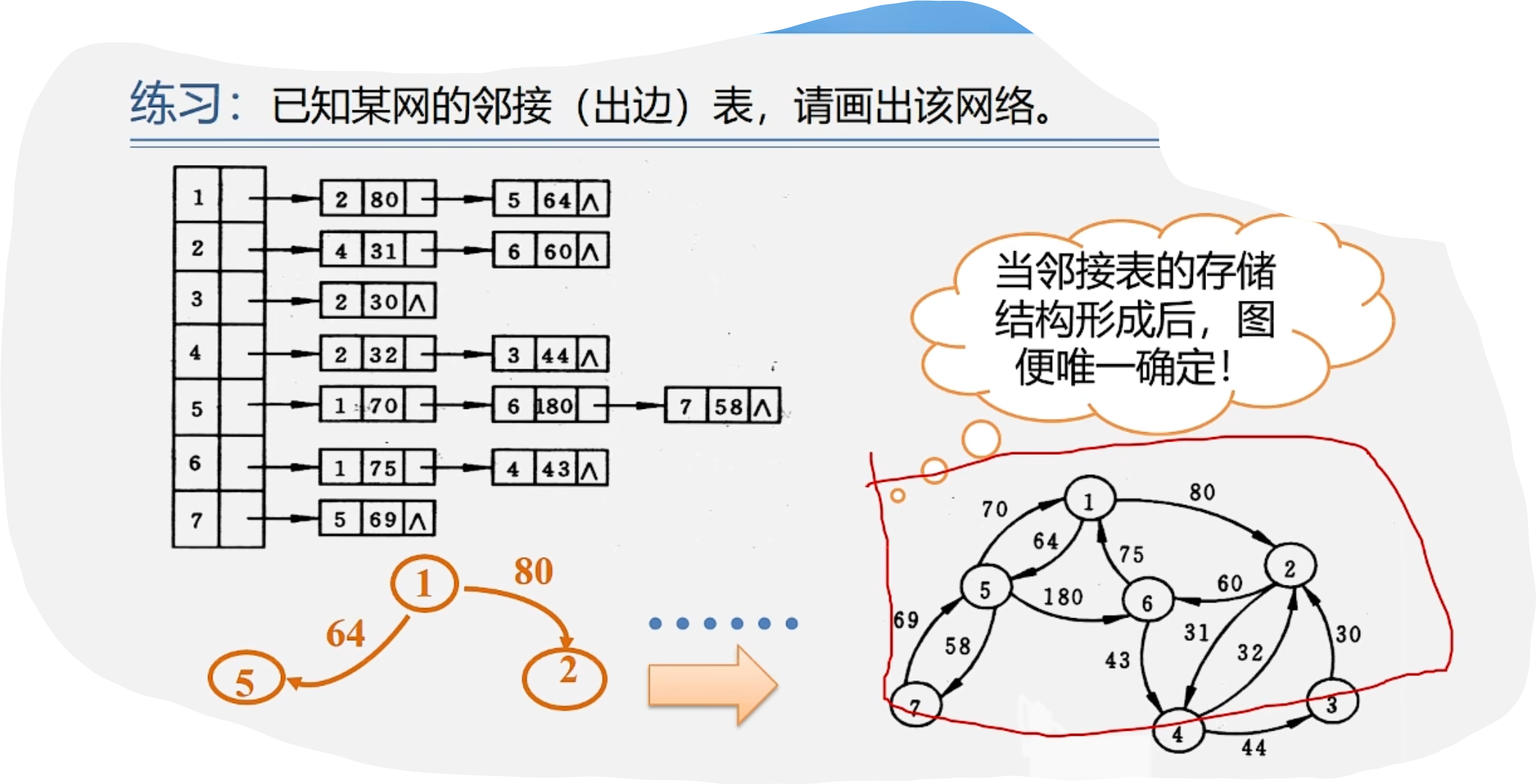
2.邻接表存储表示 

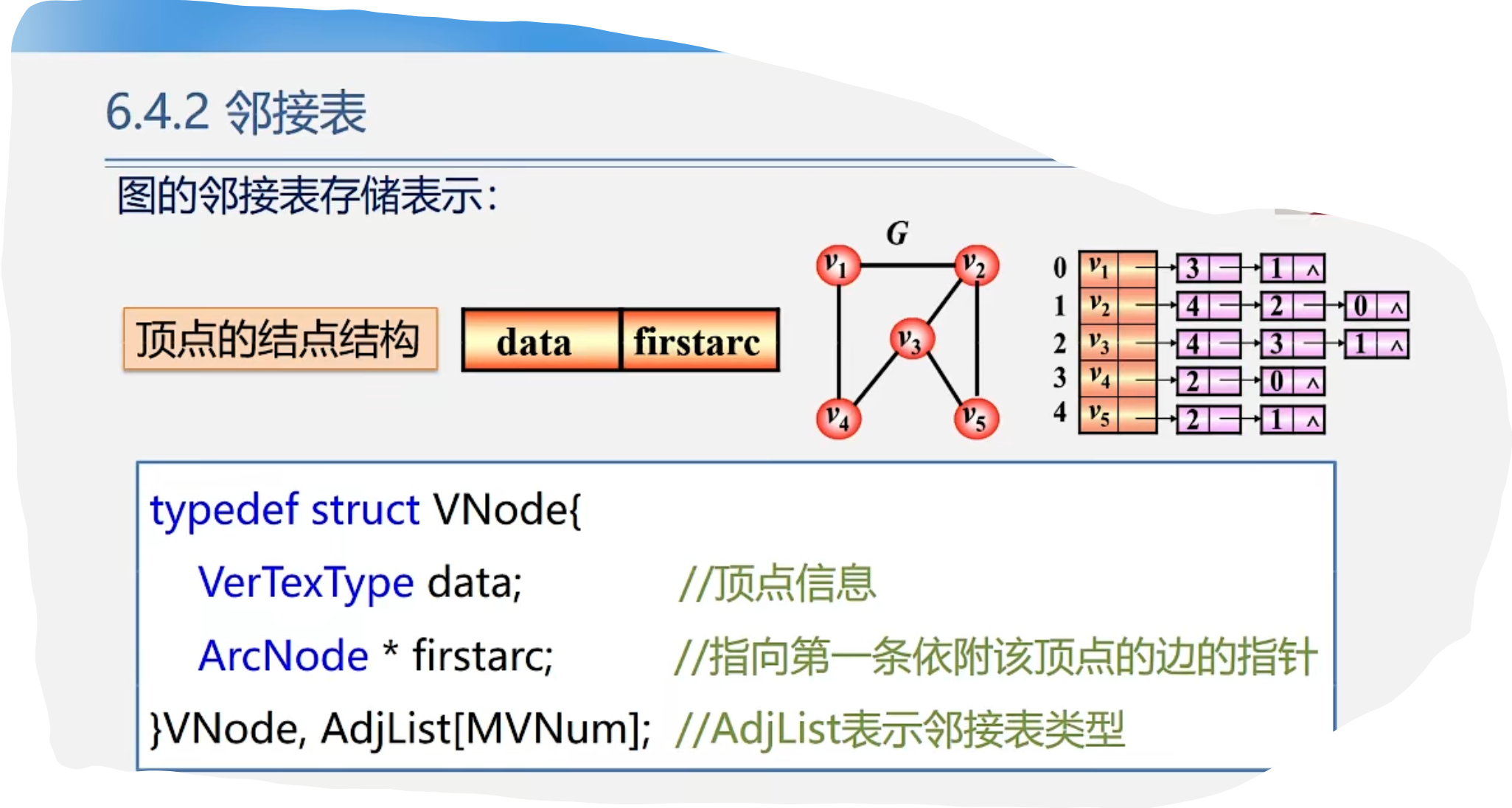
1.顶点的结点结构 

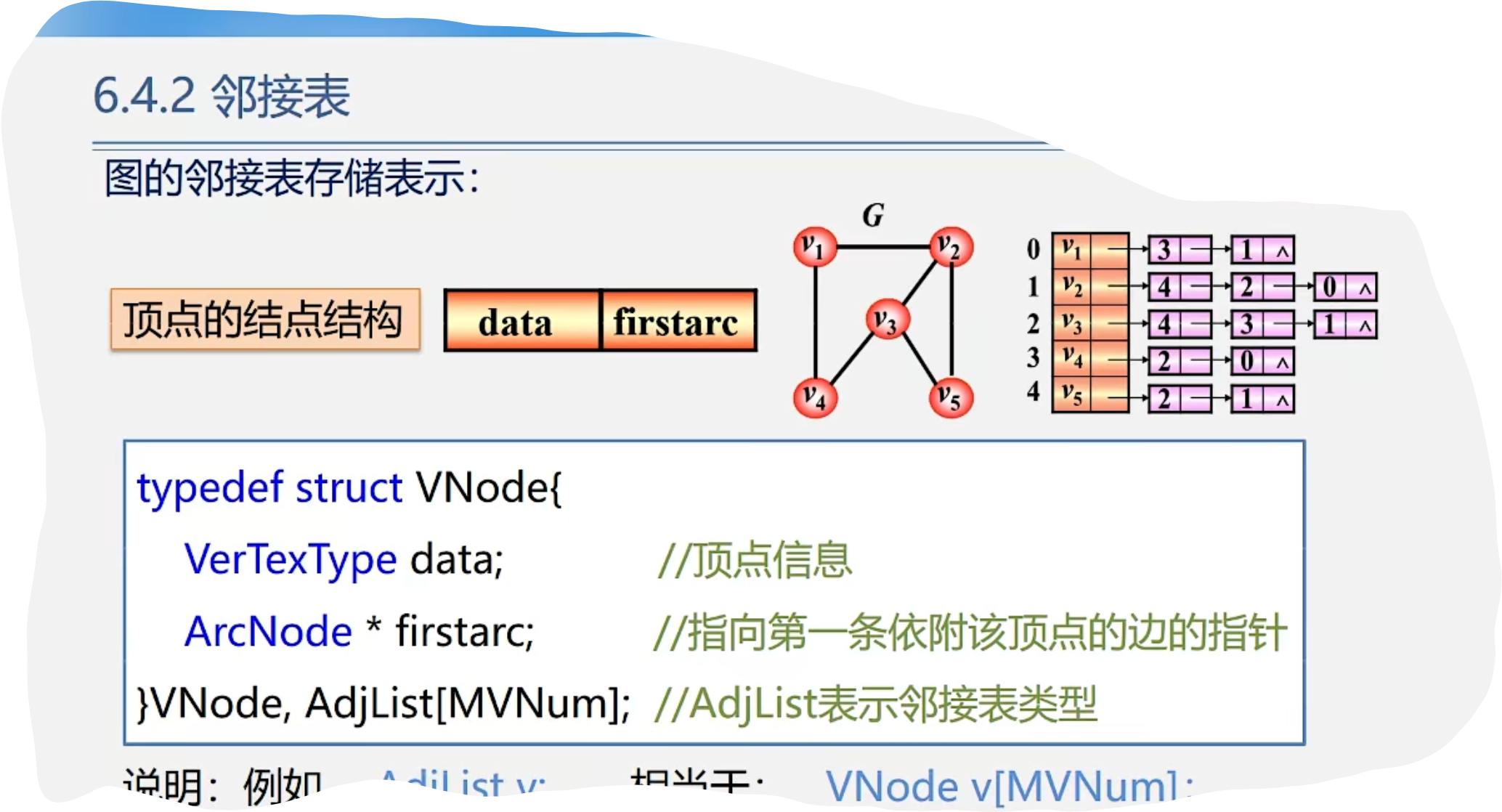
2.弧（边）的结点结构 

 3.图的结构定义

代码示例：

#define mvnum 100
typedef struct arcnode{int adjvex;struct arcnode* nextarc;int info;
}arcnode;typedef struct{char data;arcnode * firstarc;
}vnode,adjlist[mvnum];typedef struct{adjlist vertices;int vexnum,arcnum;
}algraph;

 3.邻接表操作举例

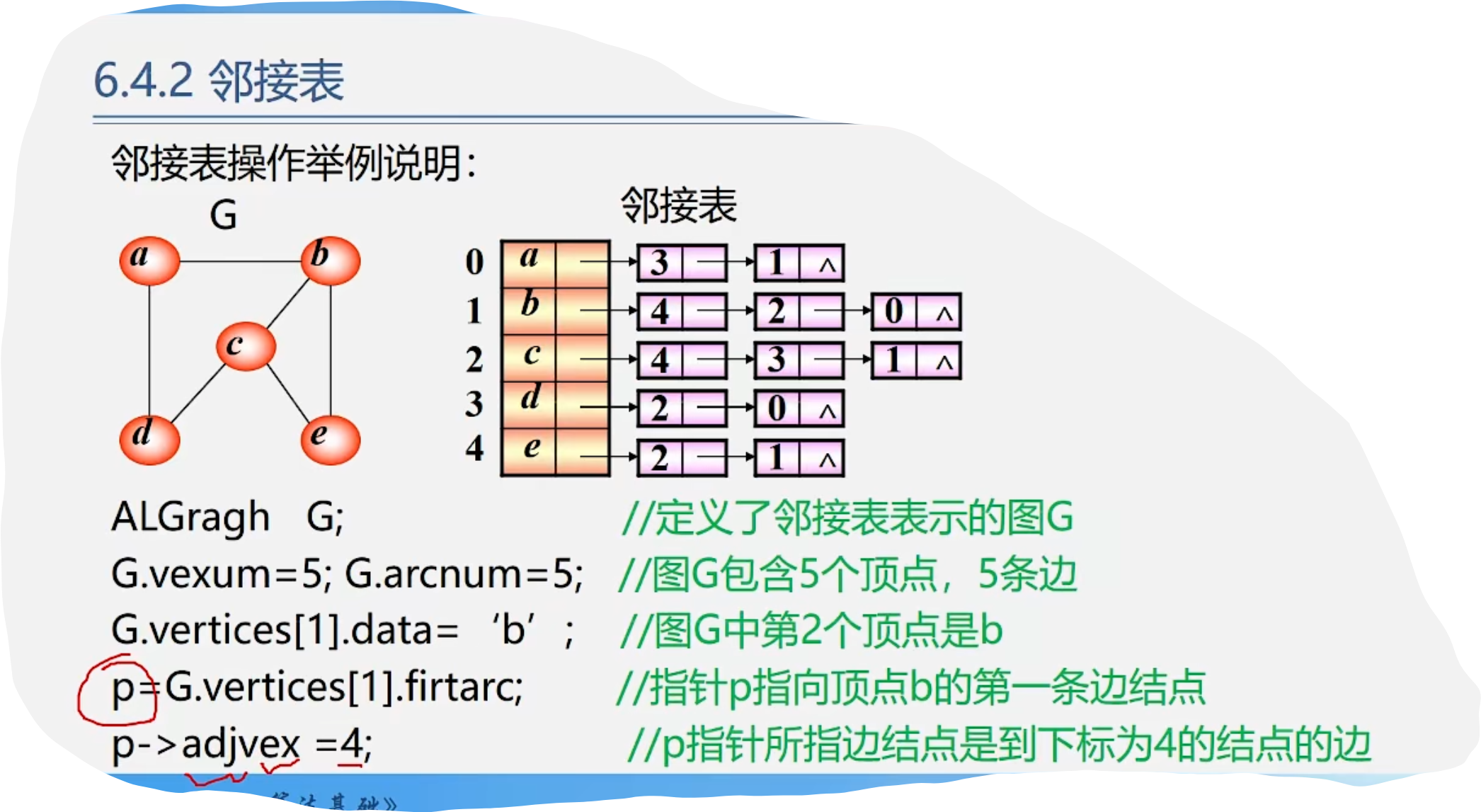
4.采用邻接表表示法创建无向网 

代码示例： 

int createudg(algraph &g)
{cin >> g.vexnum >> g.arcnum;for(int i = 1; i <= g.vexnum; i++){cin >> g.vertices[i].data;g.vertices[i].firstarc = NULL;}for(int k = 1; k <= g.arcnum; k++){cin >> v1 >> v2;int i = locatevex(g,v1);int j = locatevex(g,v2);arcnode *p1;p1 = new arcnode;p1 -> adjvex = j;p1 -> nextarc = g.vertices[i].firstarc;g.vertices[i].firstarc = p1;arcnode *p2;p2 = new arcnode;p2 -> adjvex = i;p2 -> nextarc = g.vertices[j].firstarc;g.vertices[j].firstarc = p2;}return 1;
}

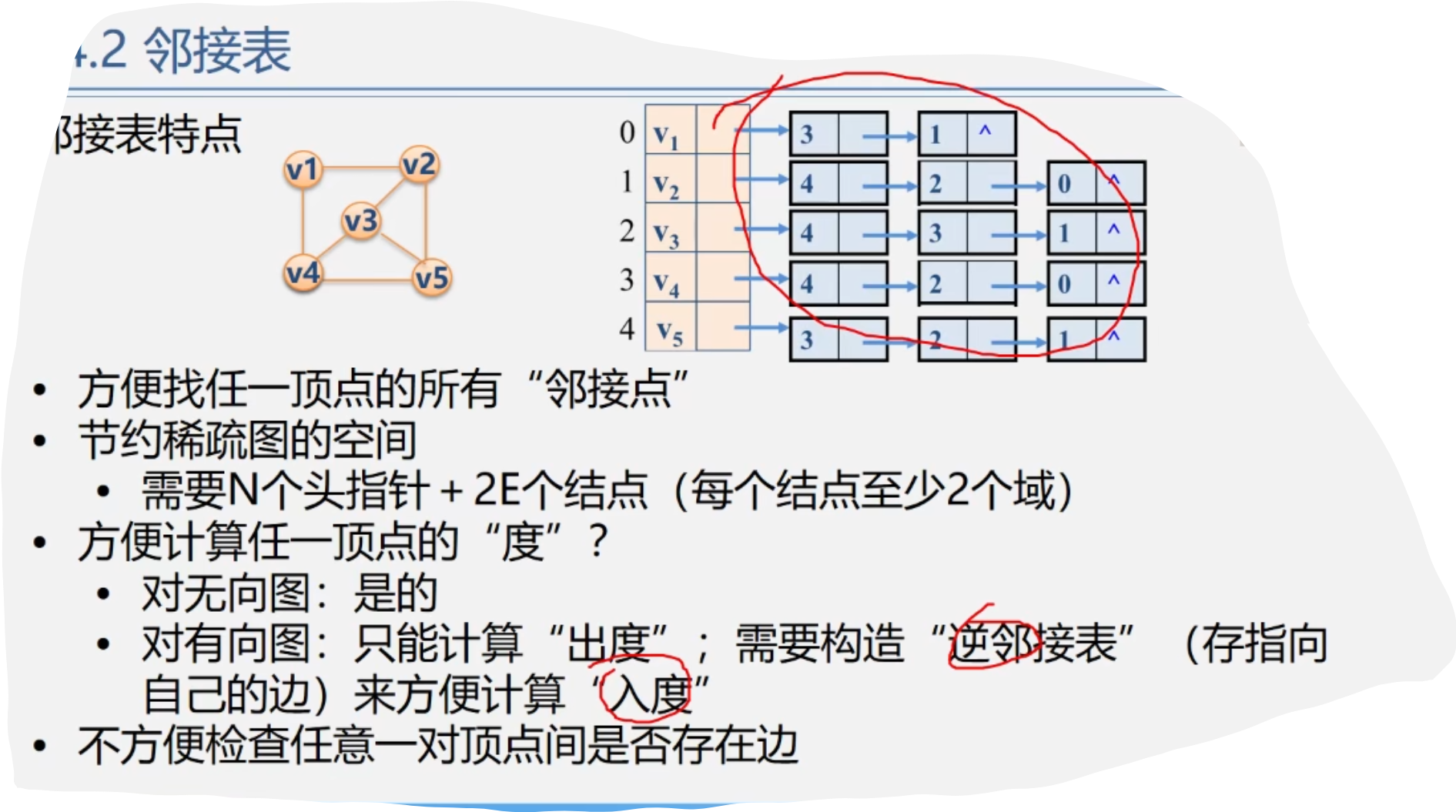
5.邻接表特点 

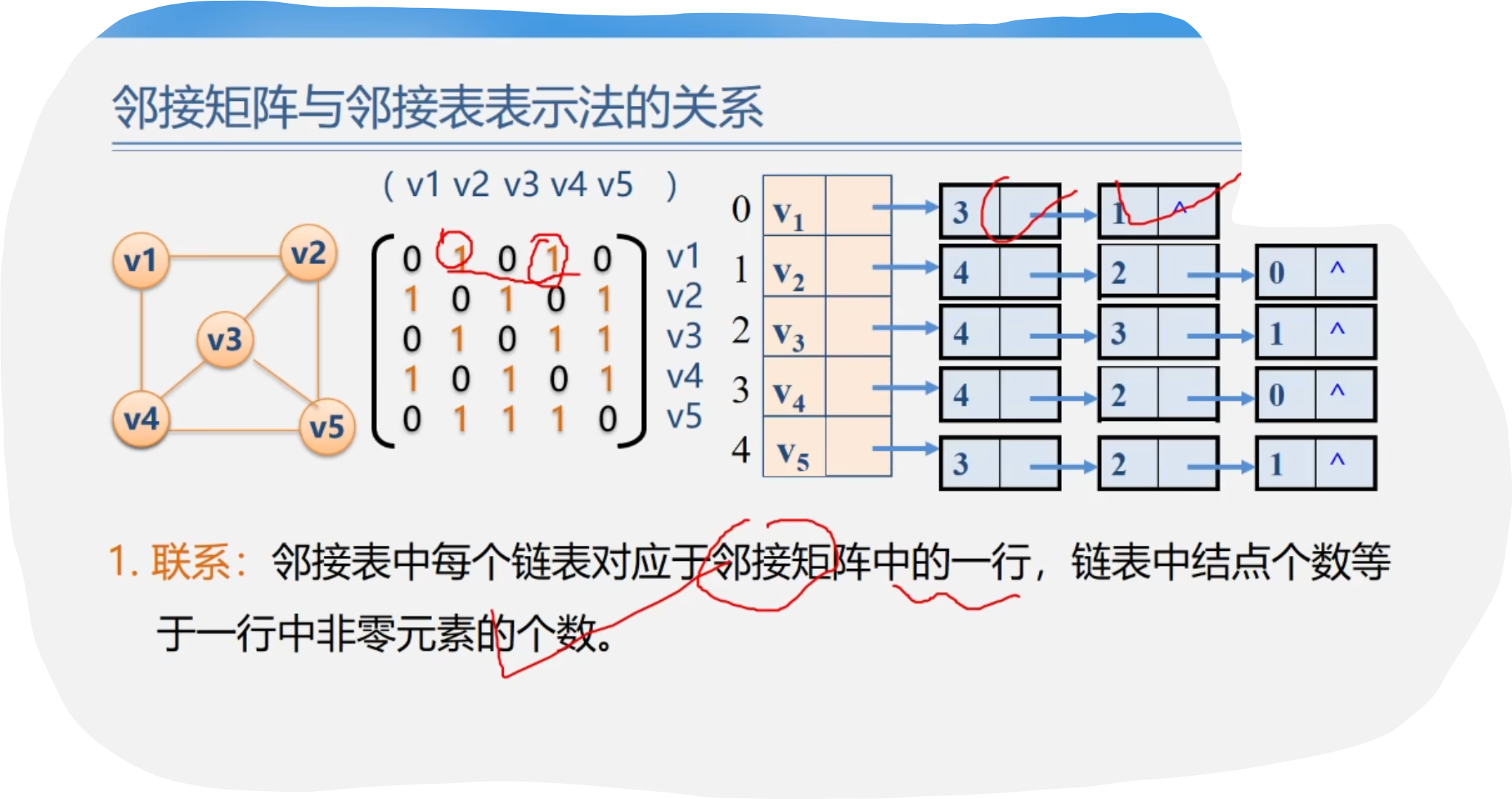
 6.临界矩阵与邻接表表示法的关系

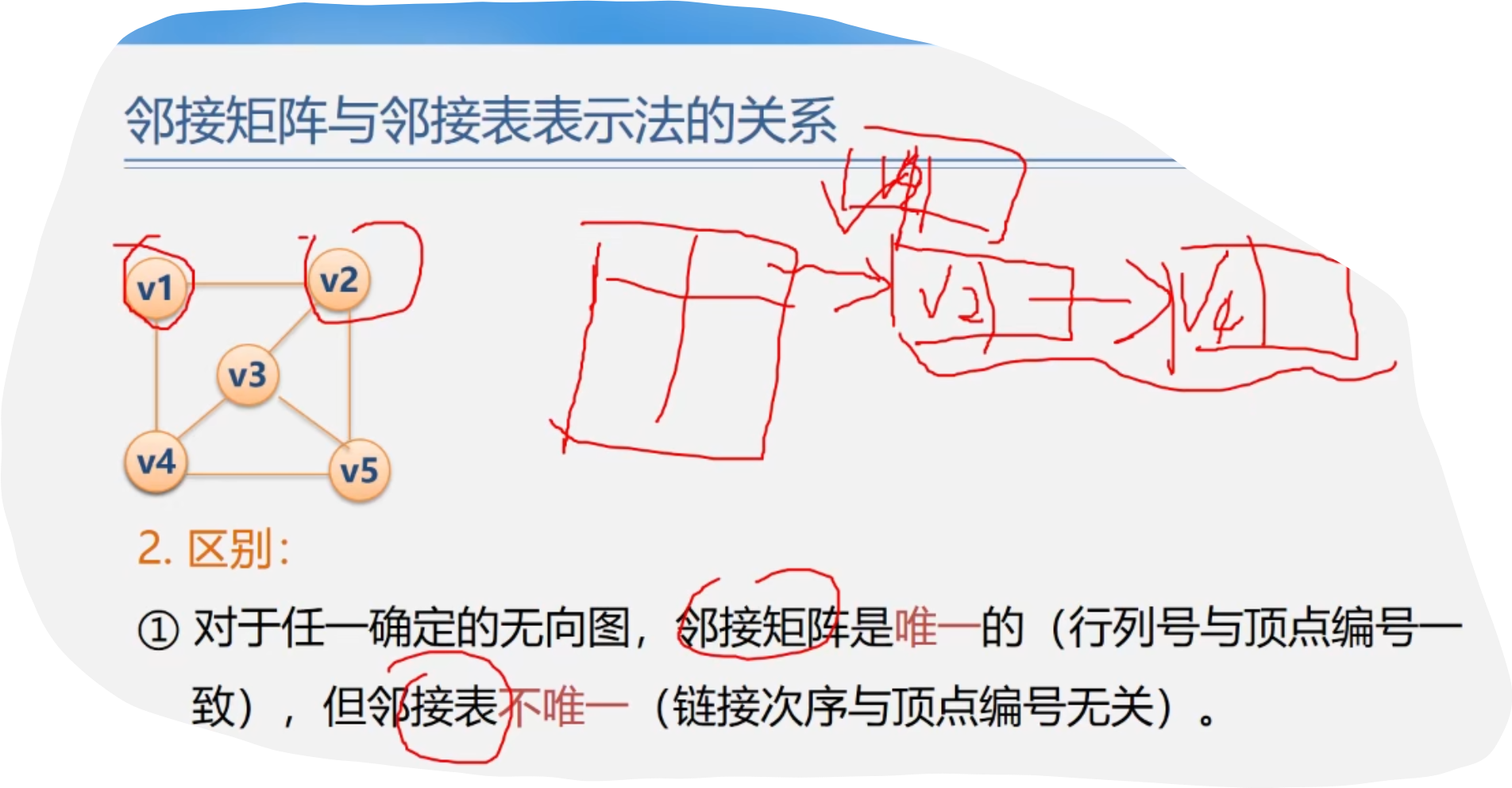
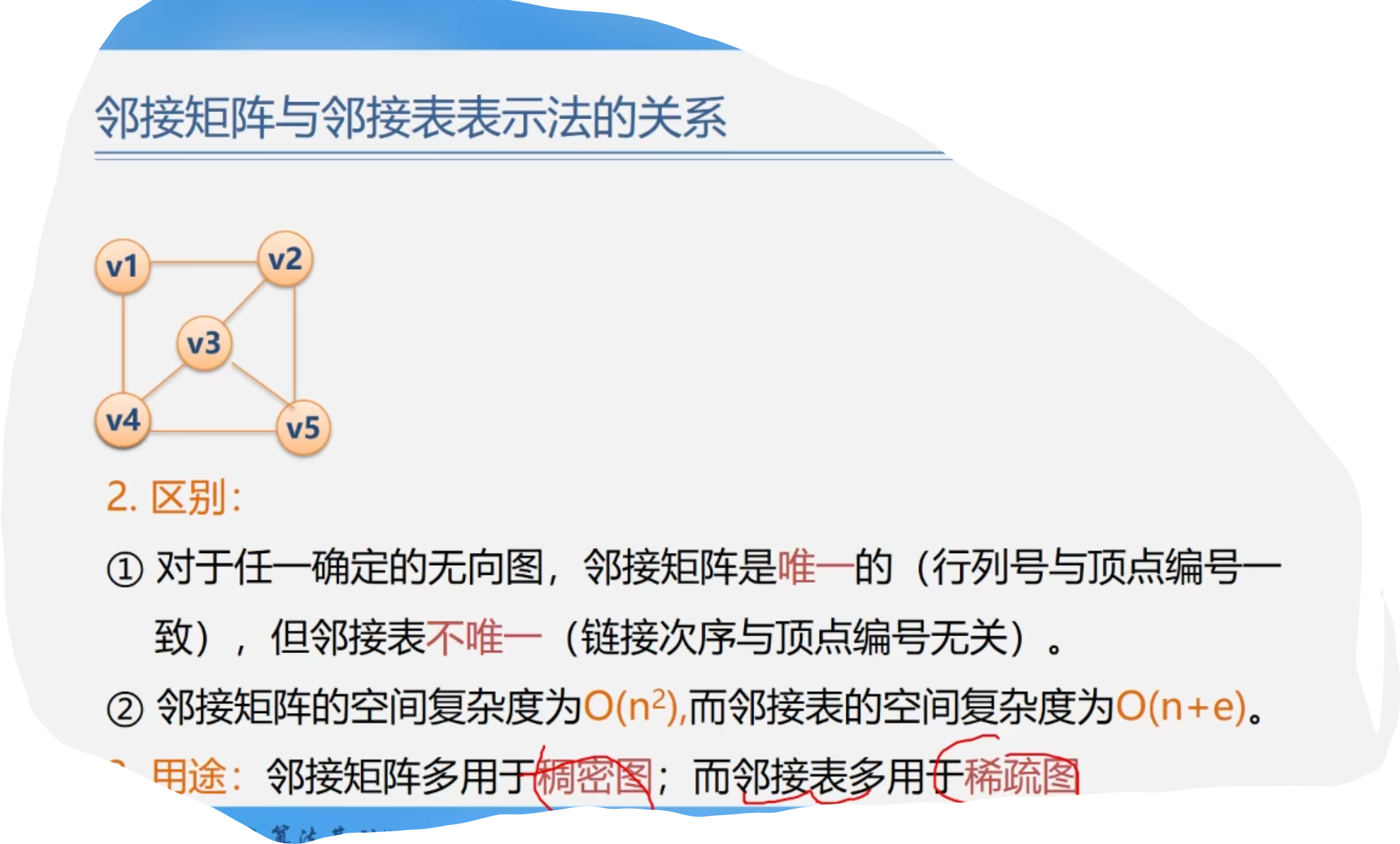
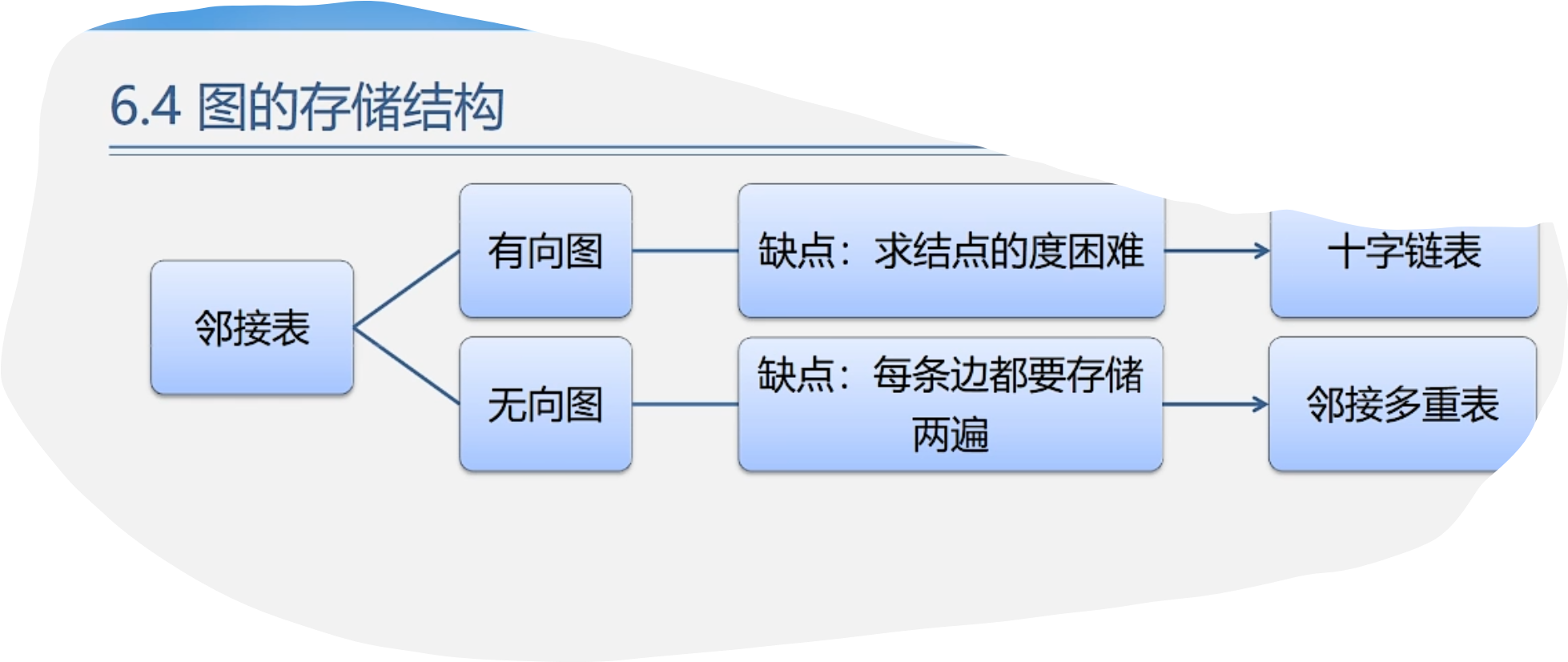
5.十字链表 （用于有向图）

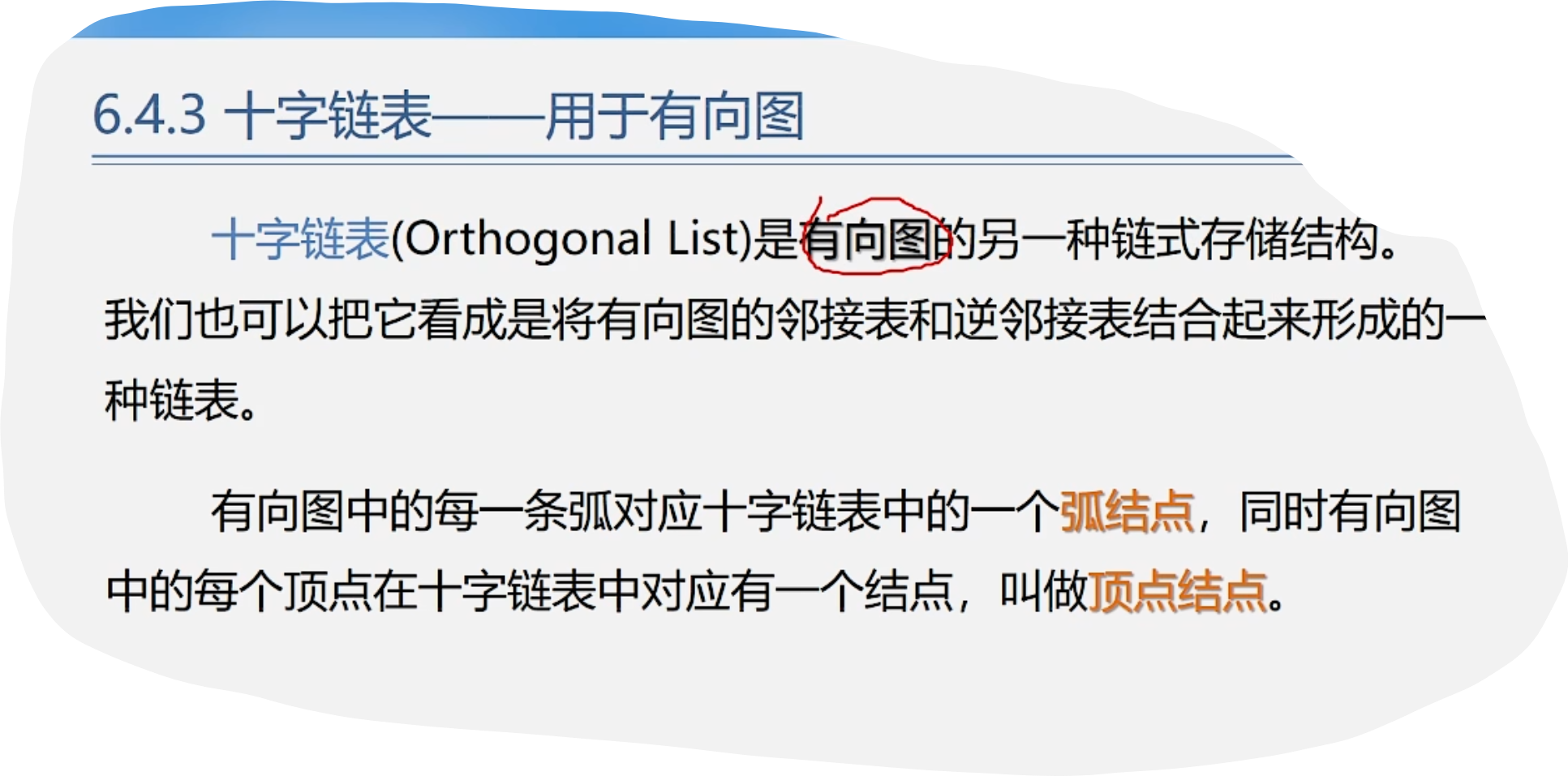
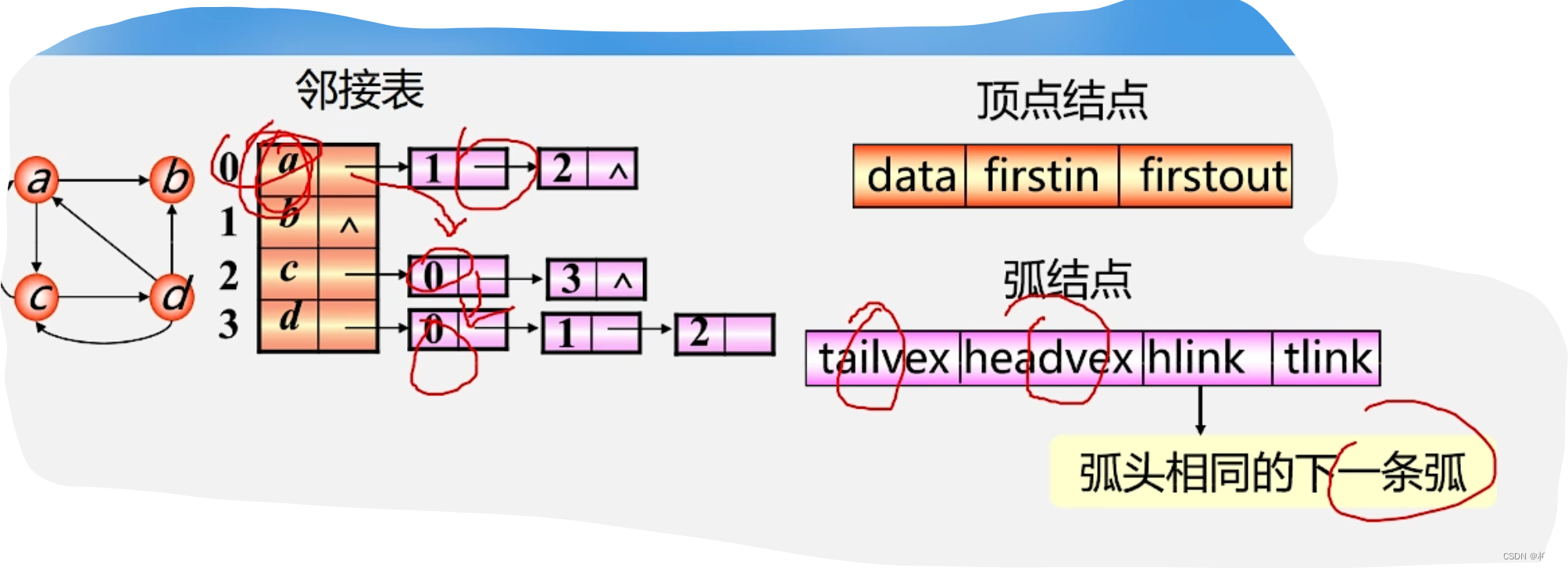
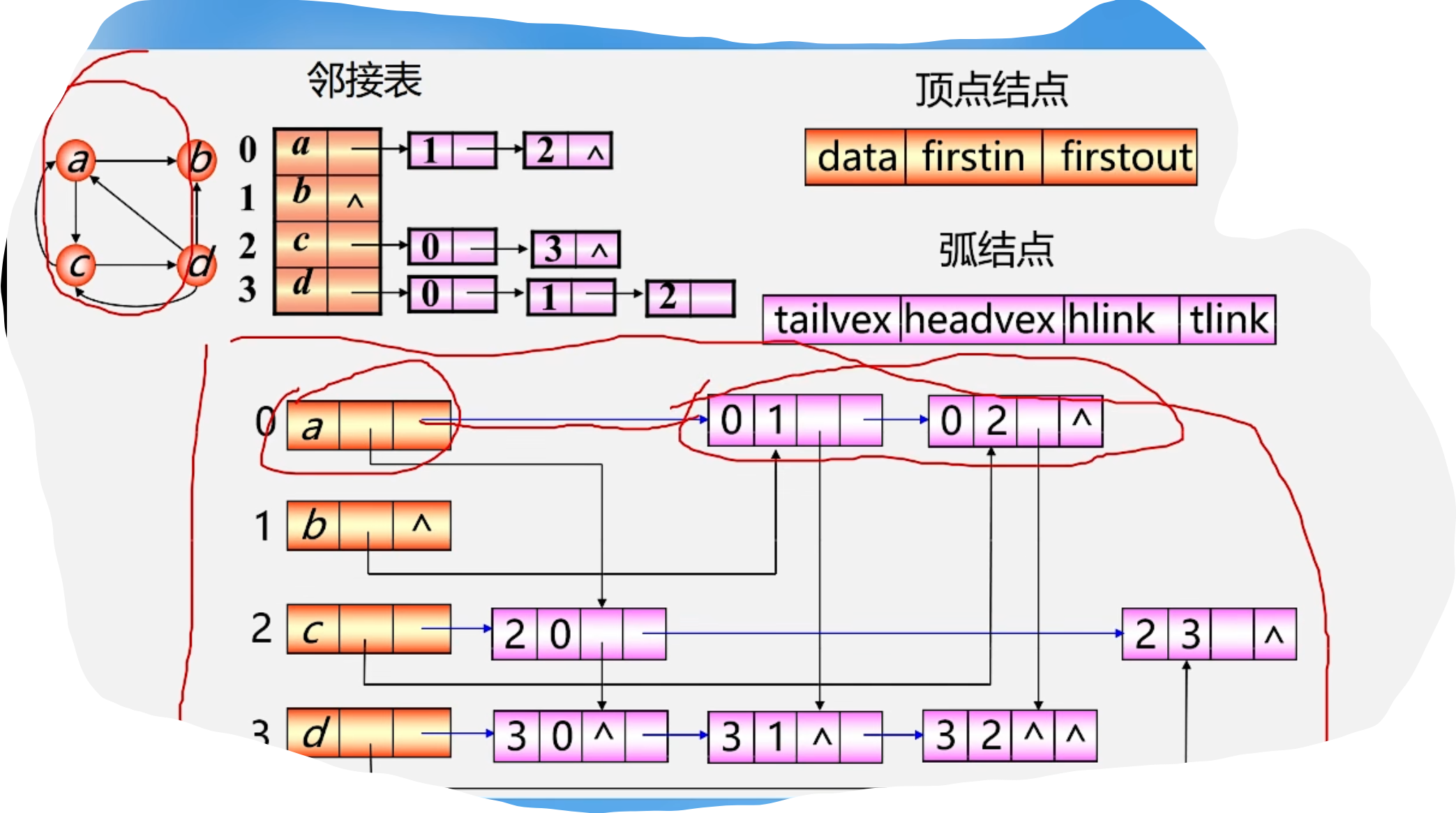
6.邻接多重表 

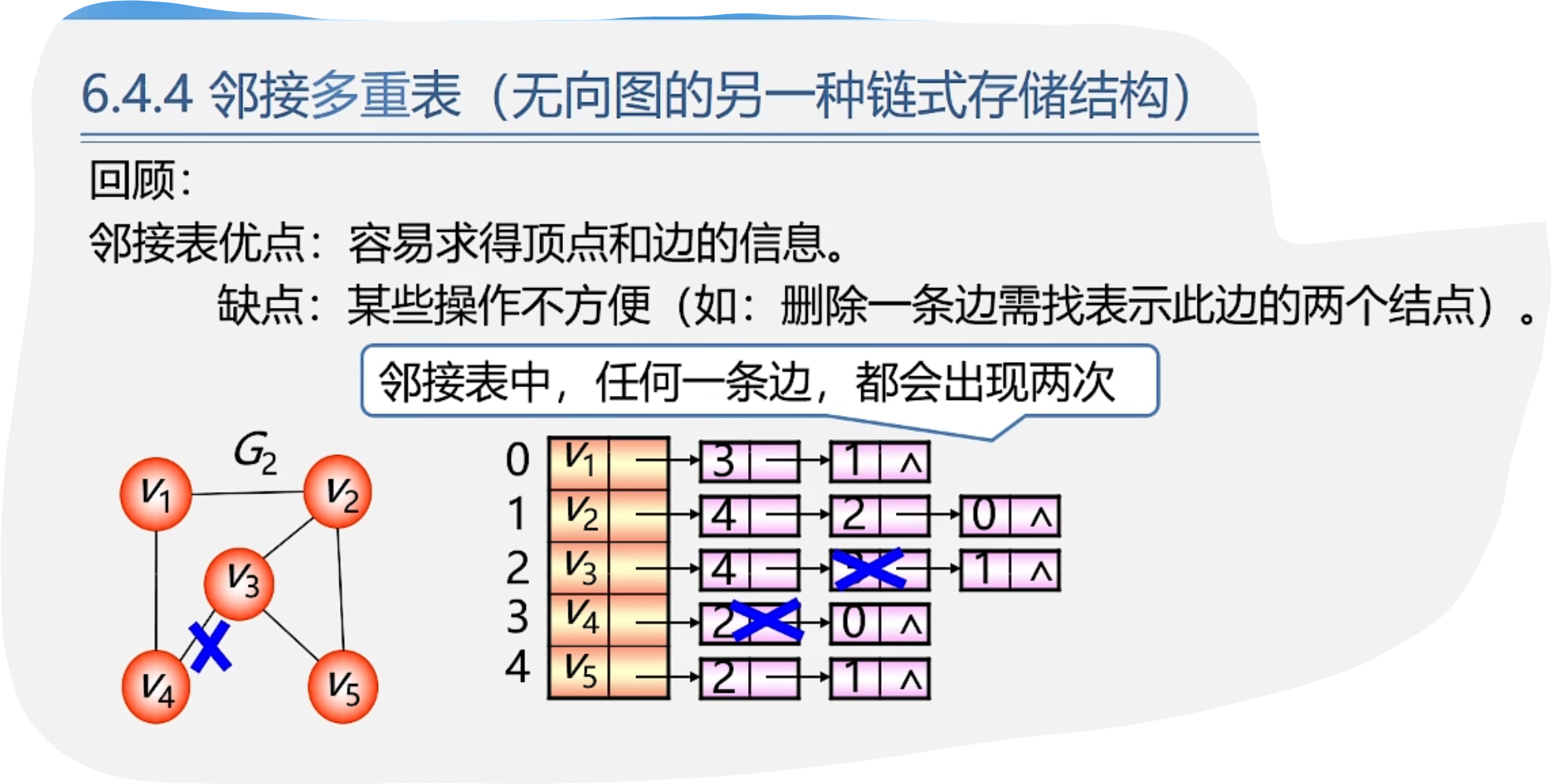
7.图的遍历 

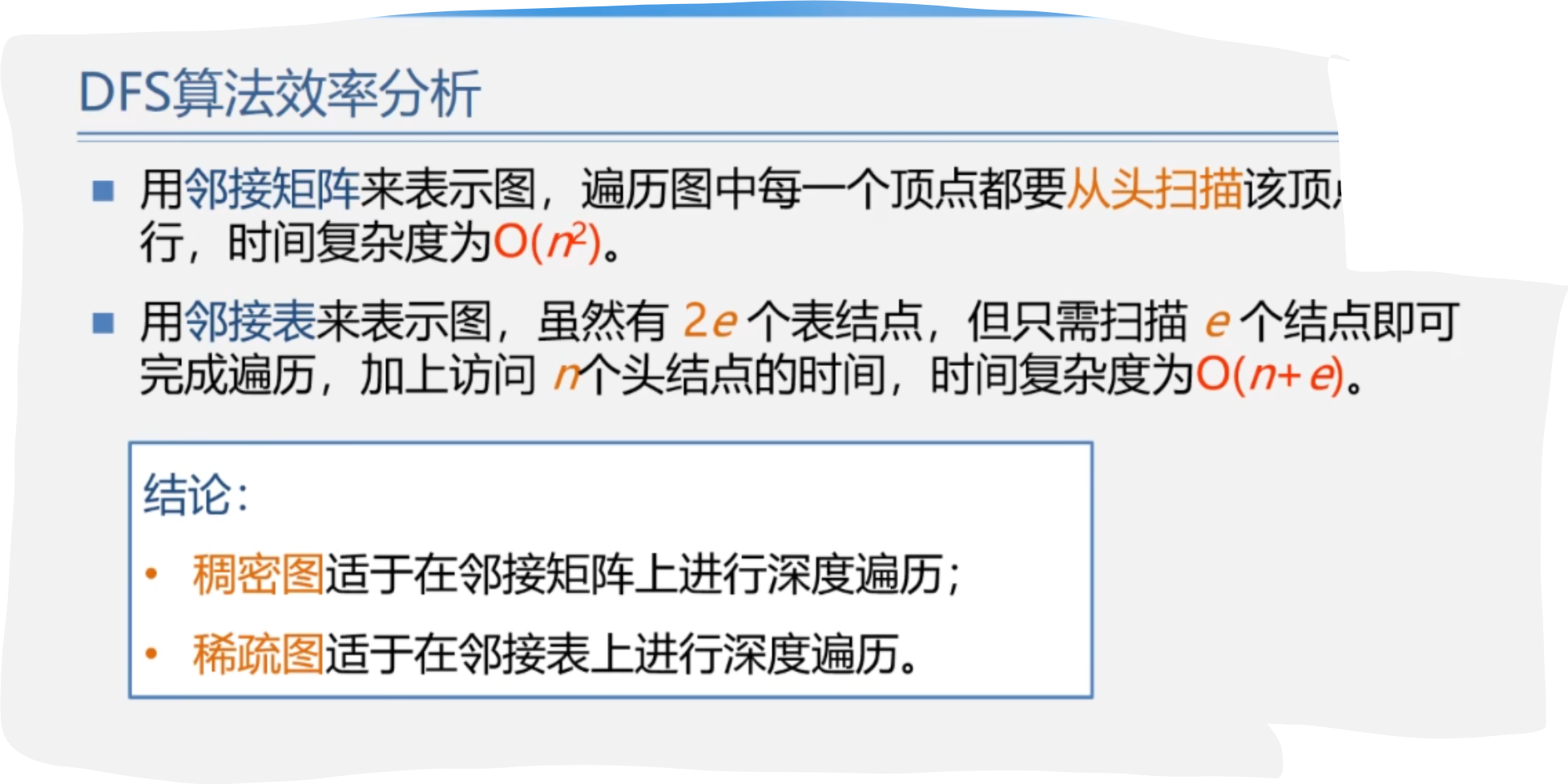
1.DFS 

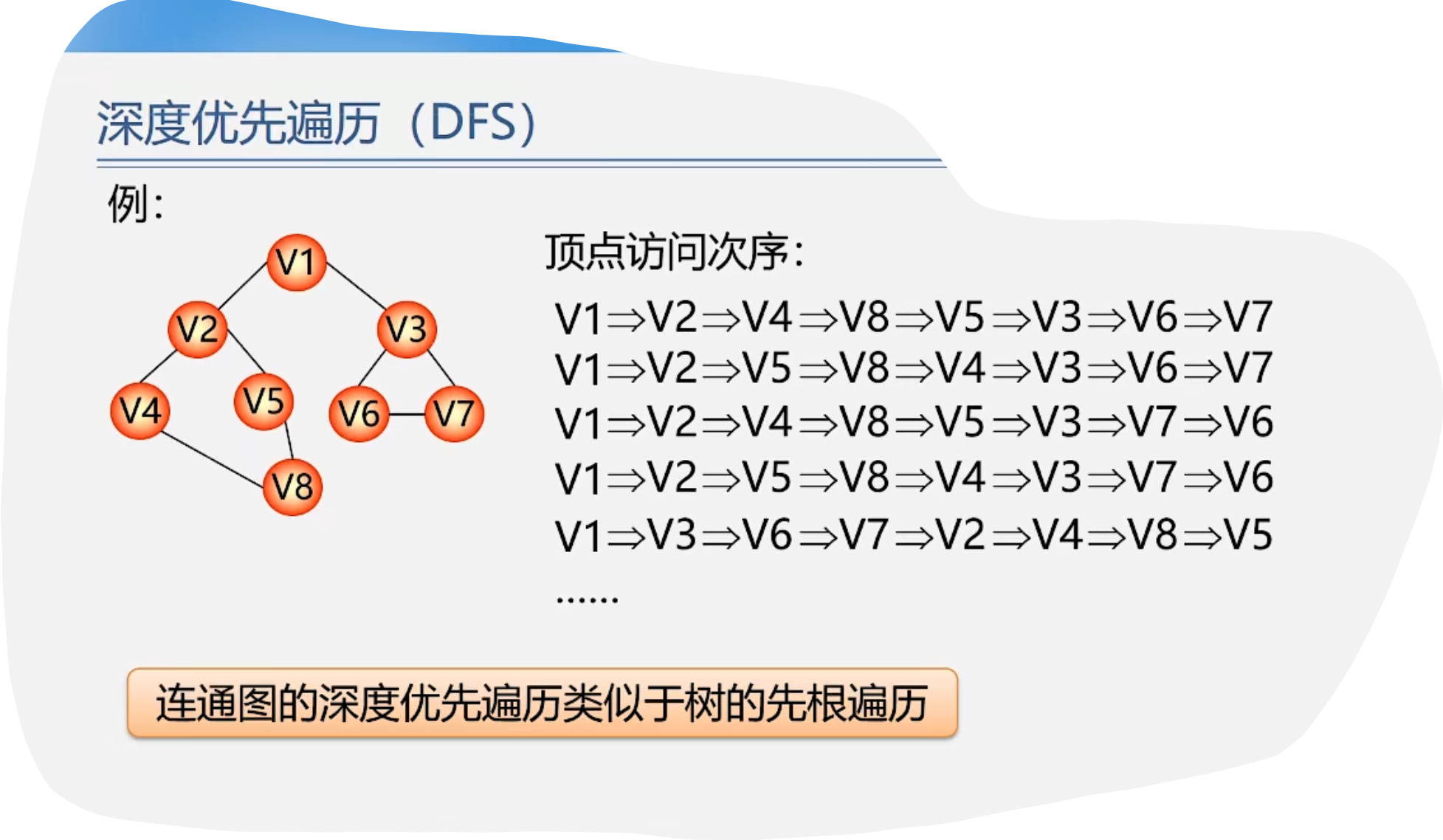
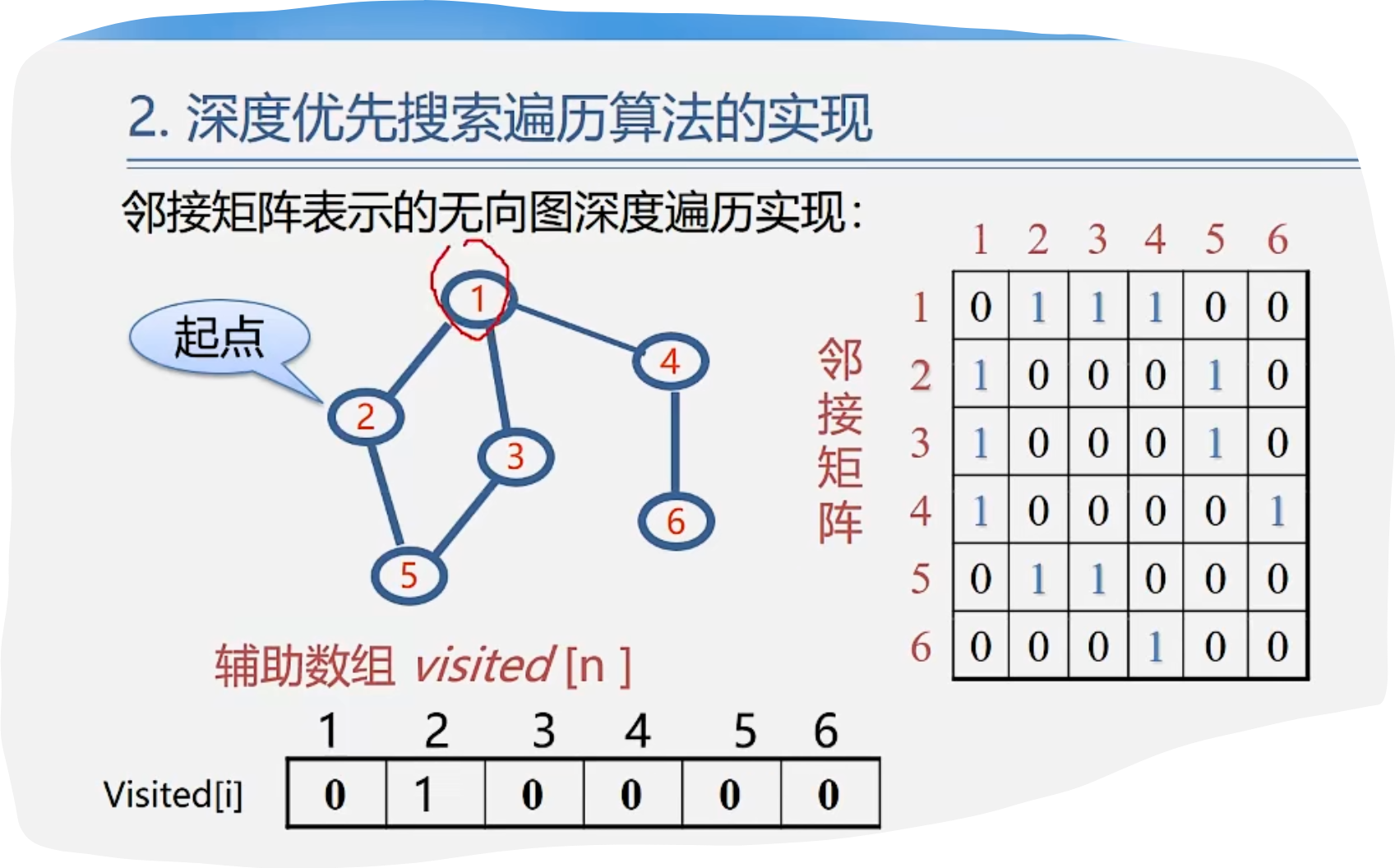
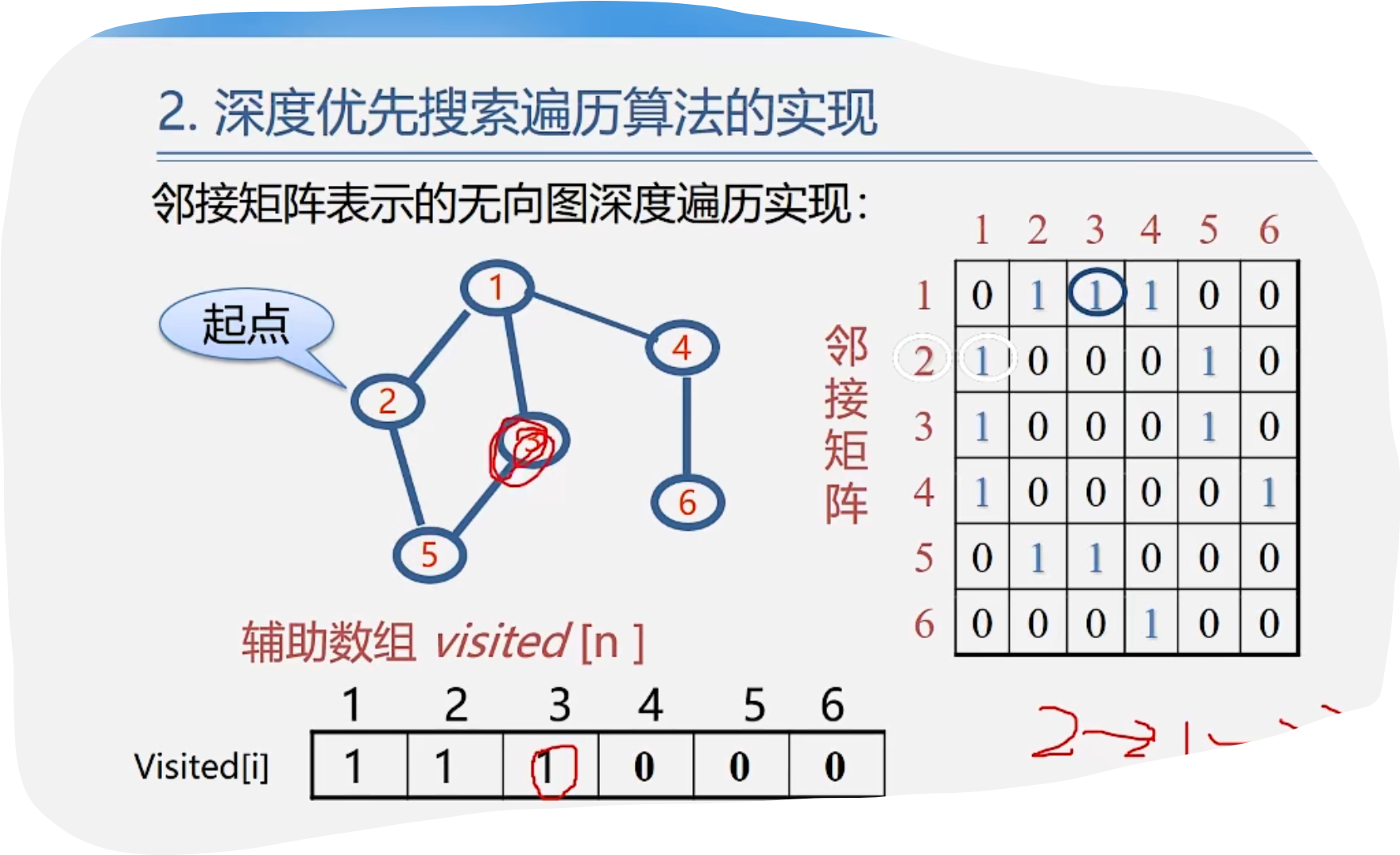
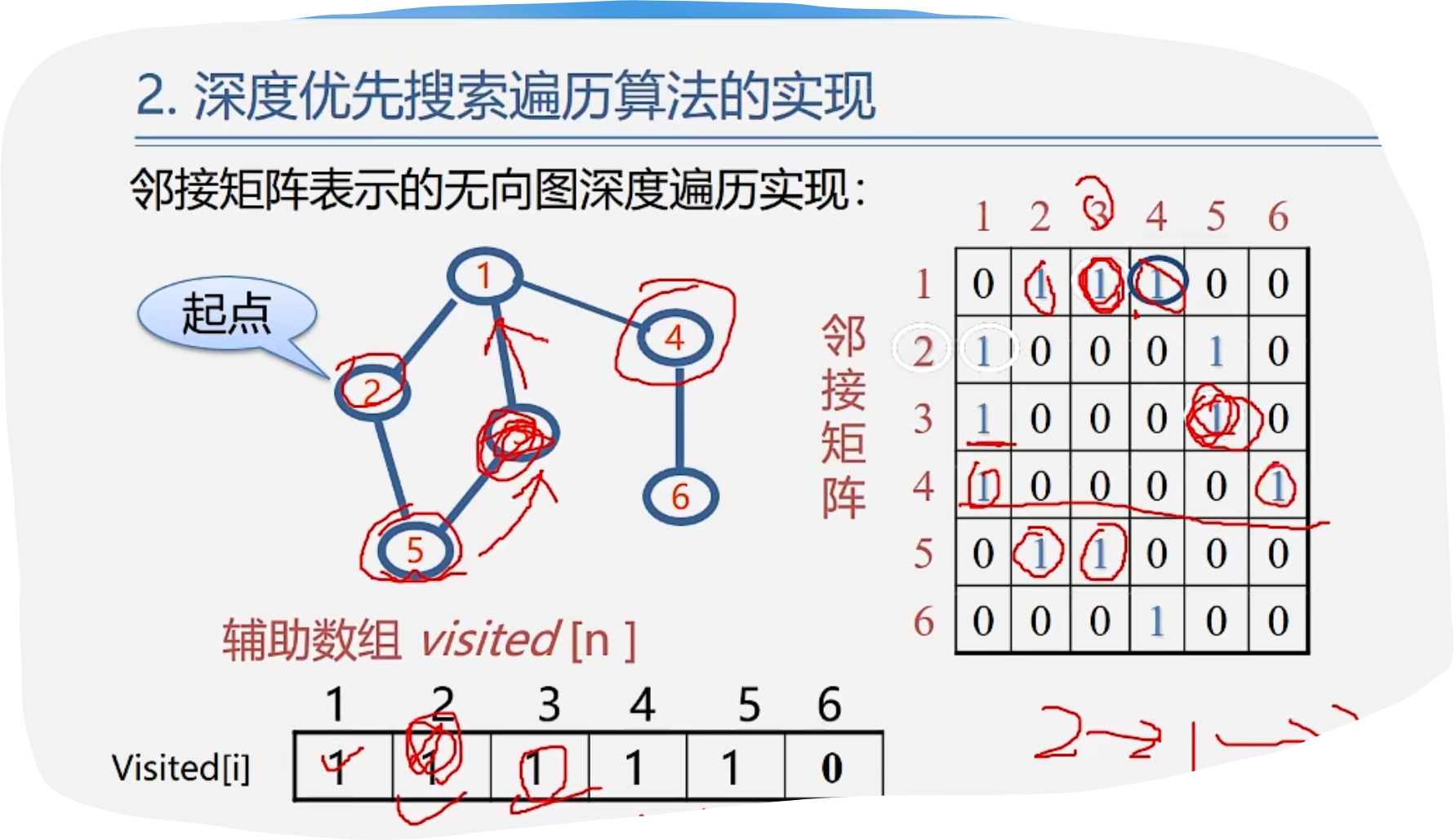
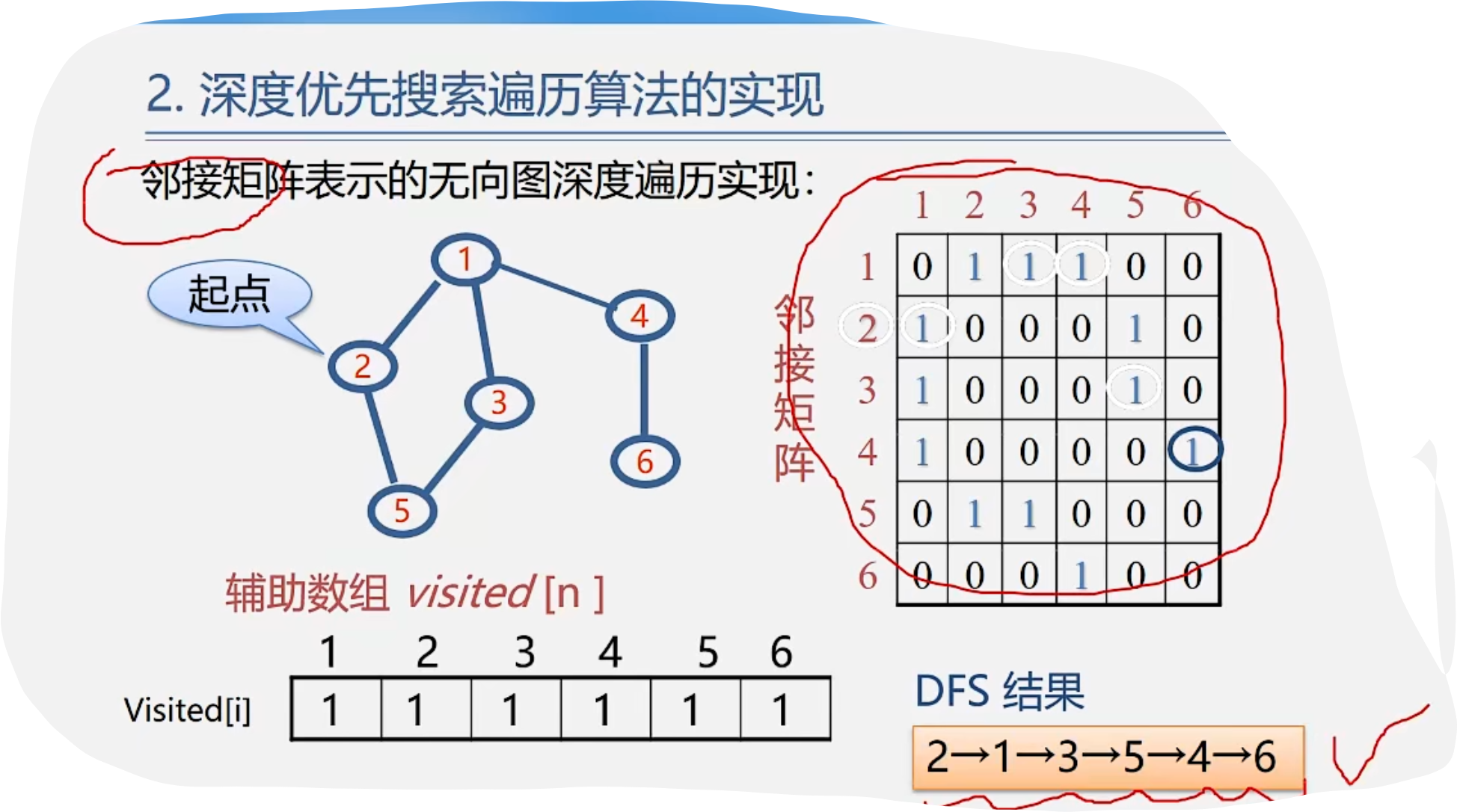
代码示例：

void dfs(amgraph g,int v)
{cout << v;visited[v] = true;for(int w = 0; w < g.vexnum; w++){if(g.arcs[v][w] != 0 && !visited[w]) dfs(g,w);}
}

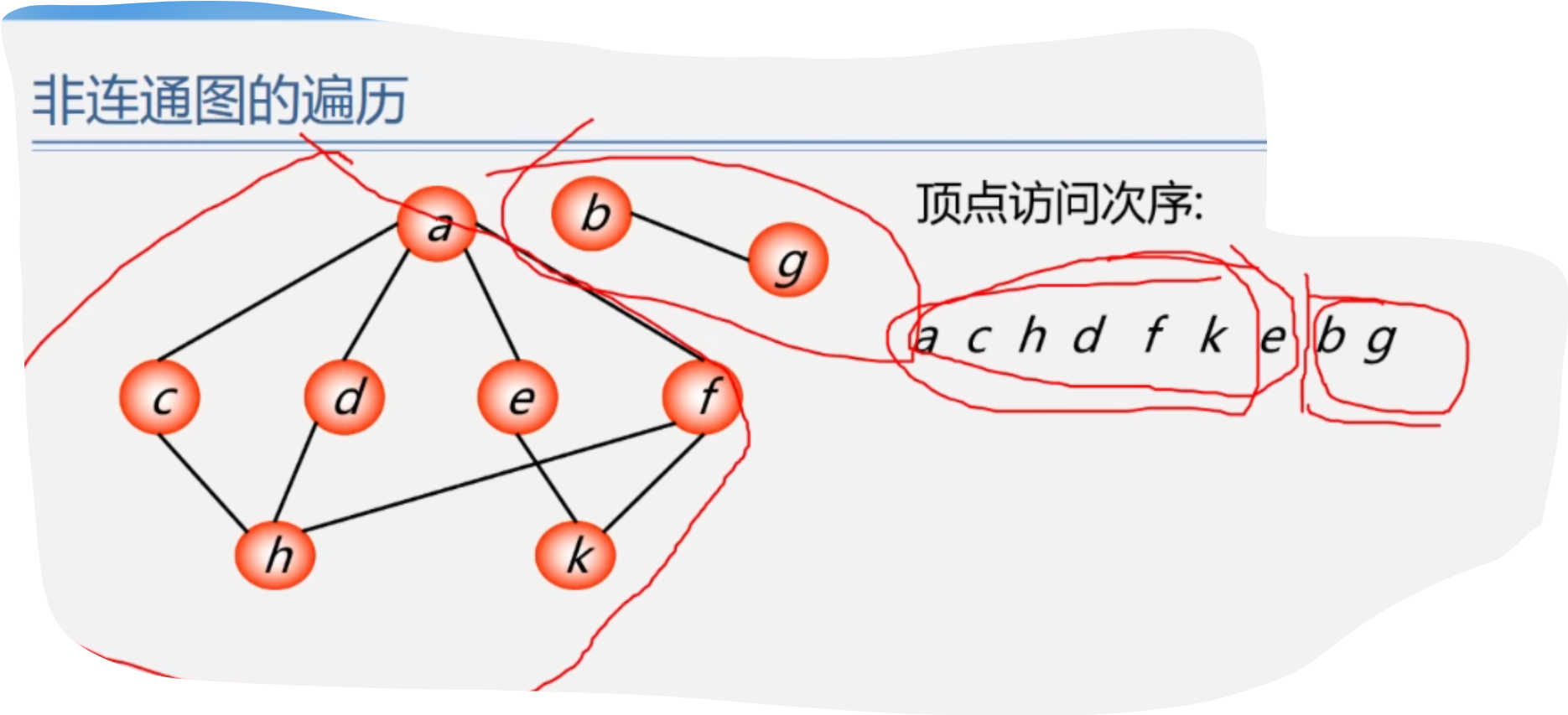
2.BFS 

  

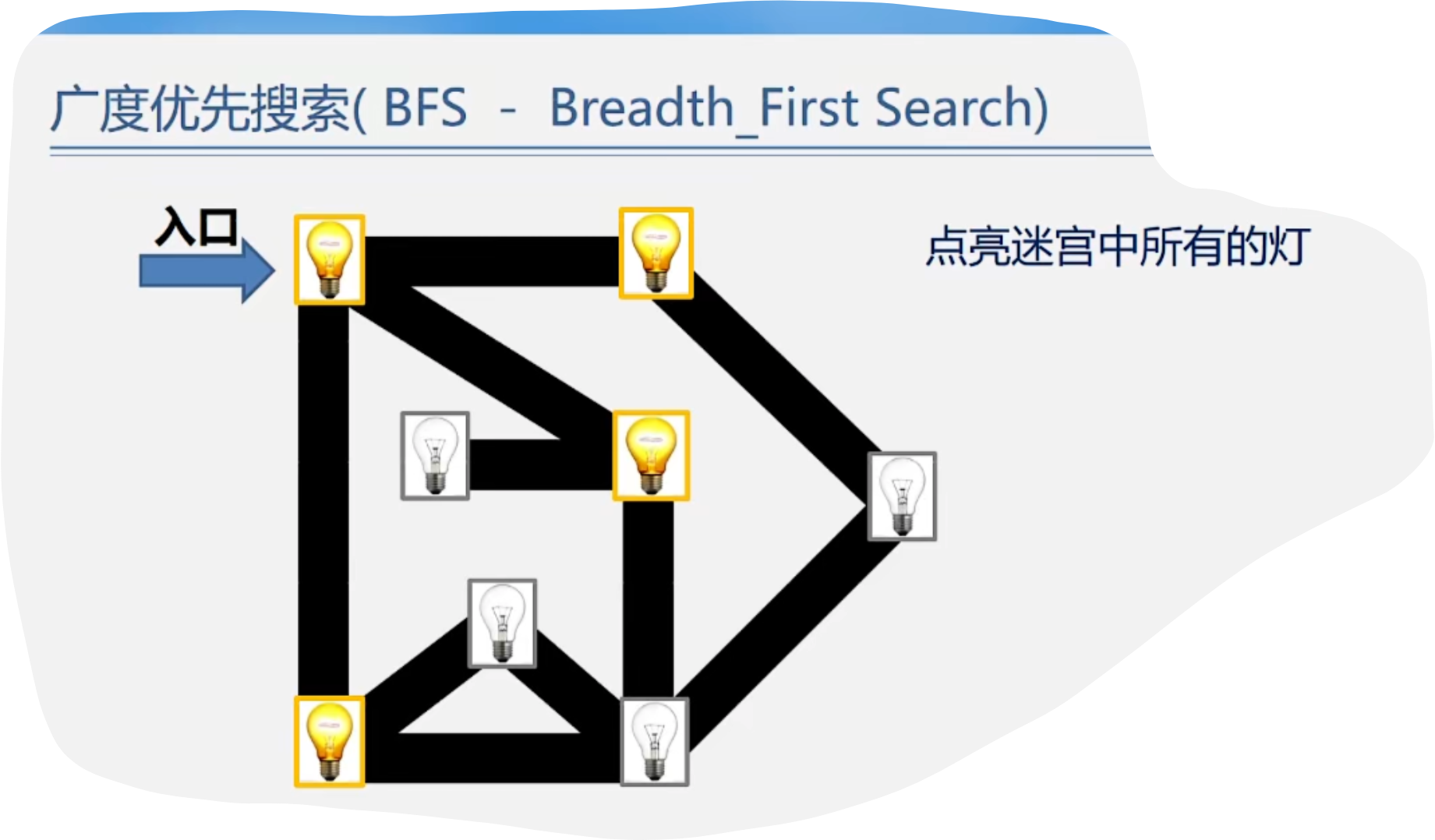
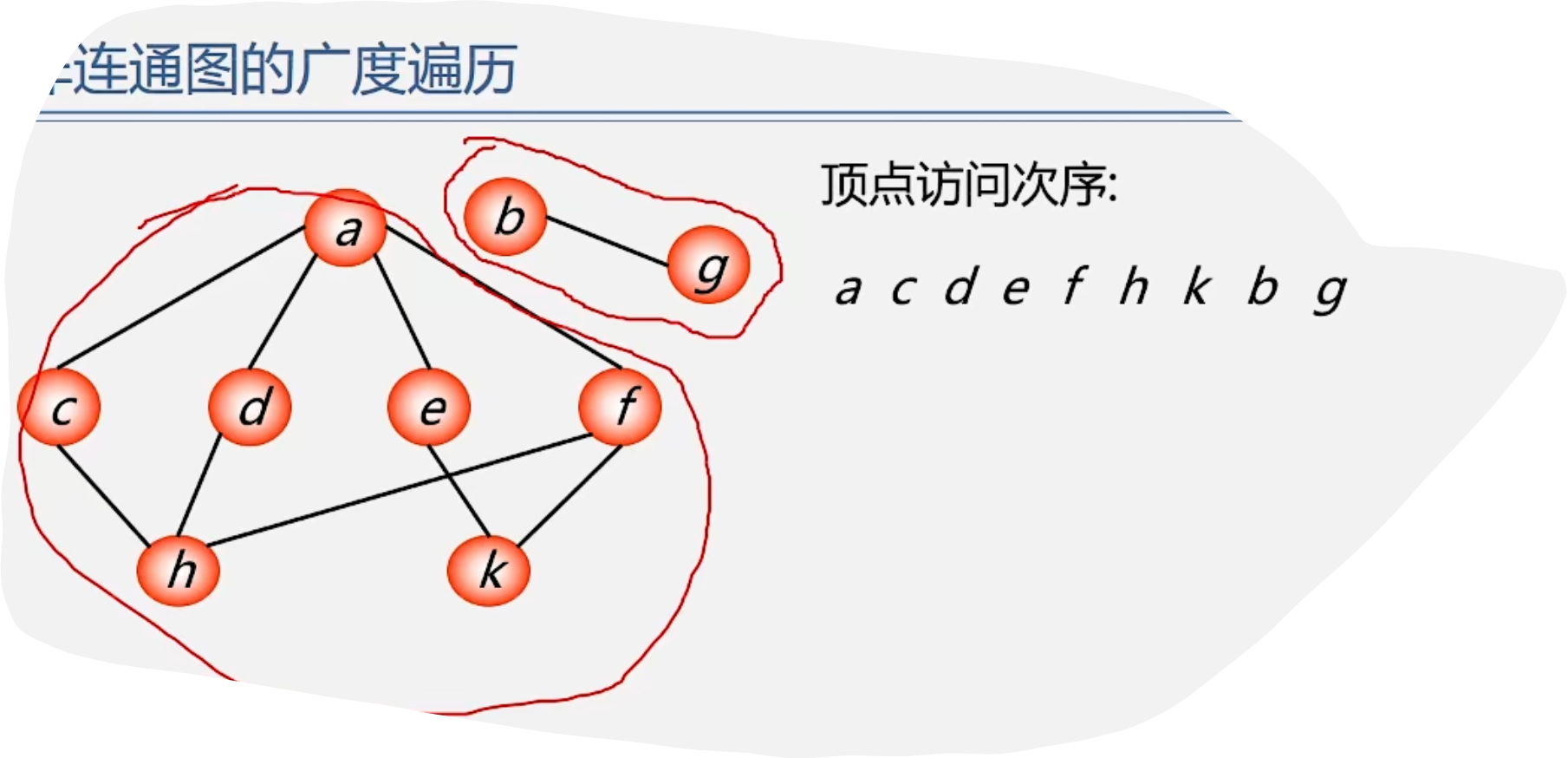
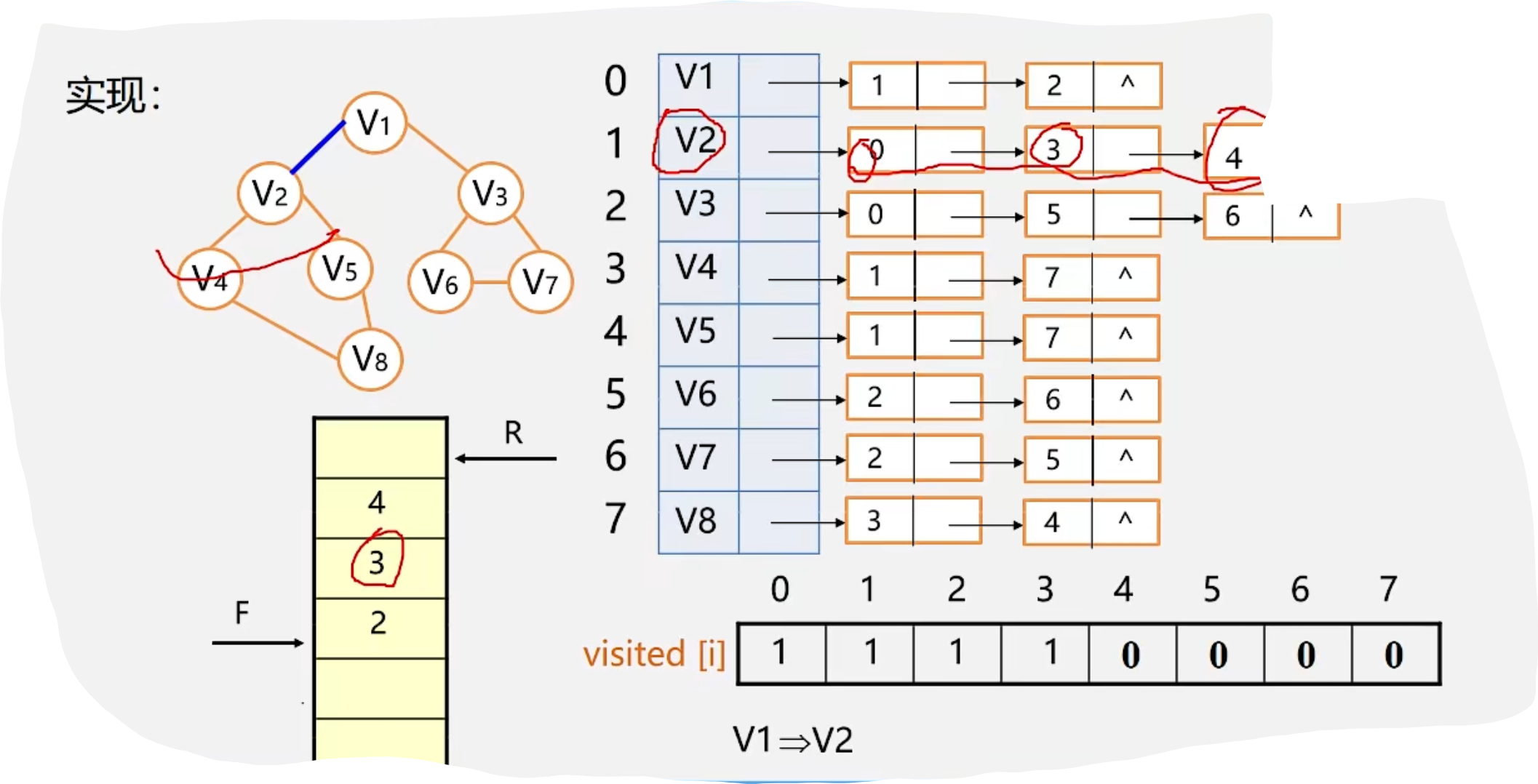
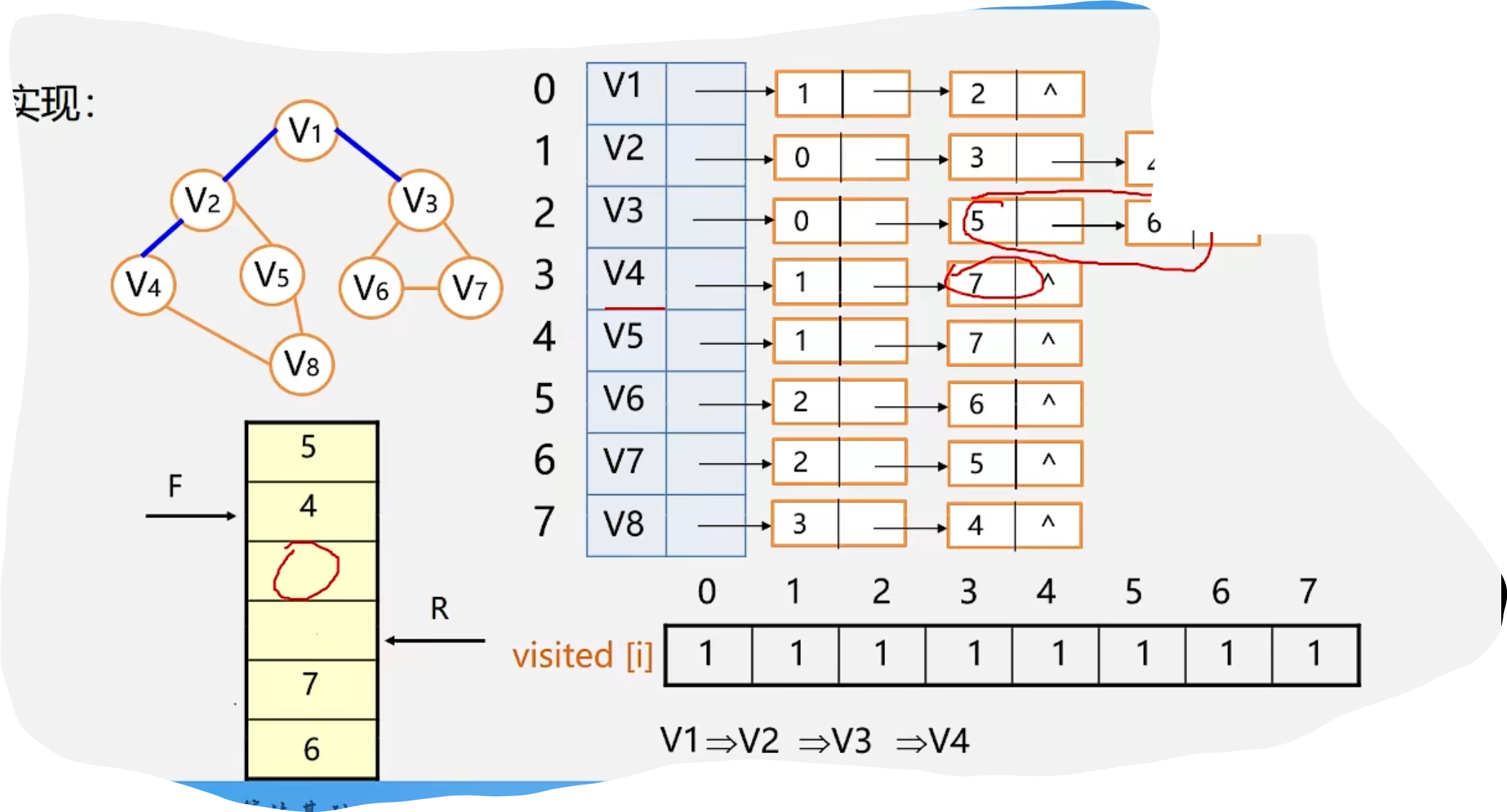
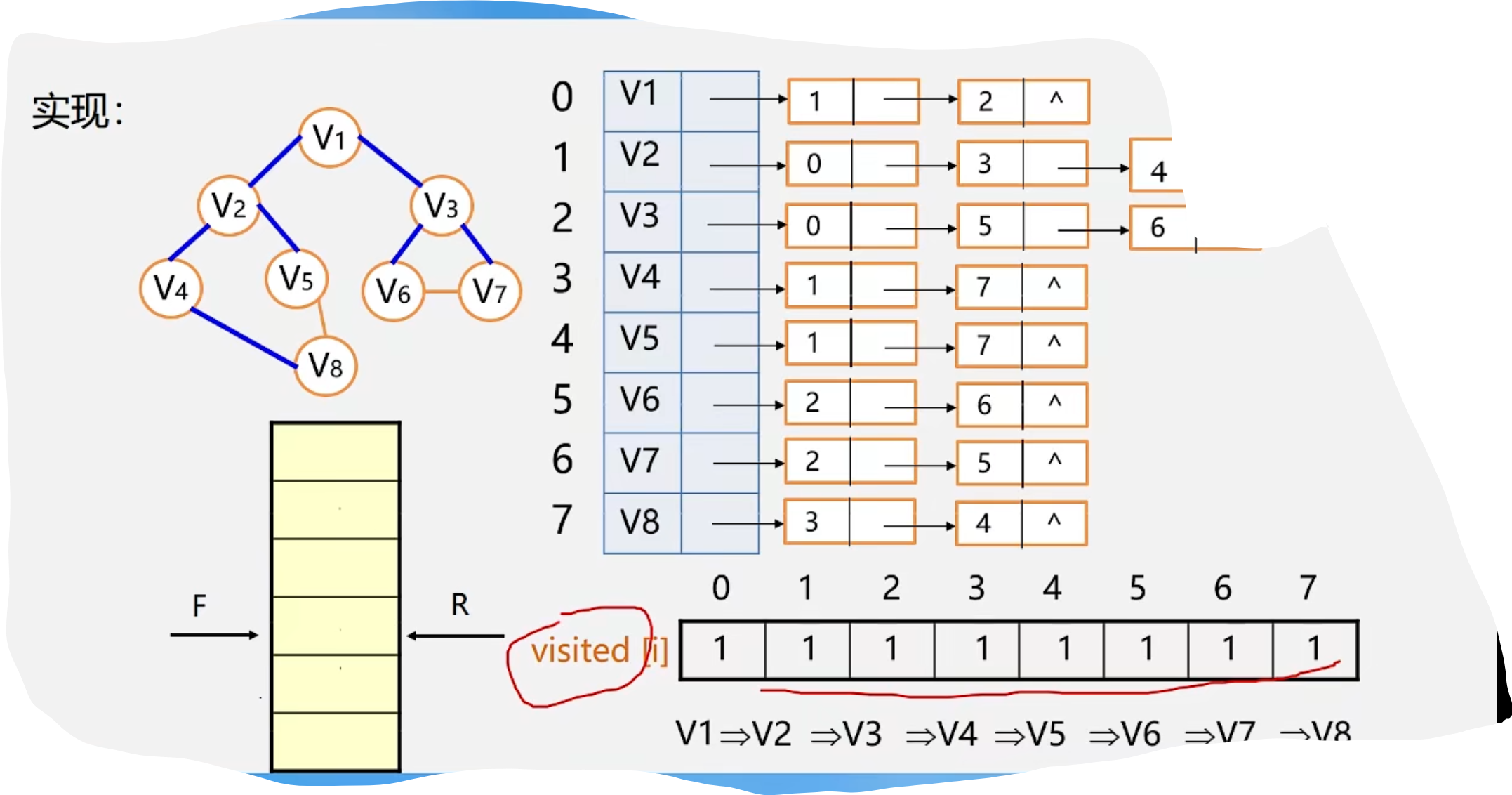
代码示例：

void bfs(graph g,int v)
{cout << v;visited[v] = true;initqueue(q);enqueue(q,v);while(!queueempty(q)){dequeue(q,u);}for(int w = firstadjvex(g,u); w > 0; w = nextadjvex(g,u,w)){if(!visited[w]){cout << w;visited[w] = true;enqueue(q,w);}}
}

8.总的代码

#include <iostream>
using namespace std;typedef struct{char vexs[100];int arcs[32767][32767];int vexnum,arcnum;
}amgraph;int locatevex(amgraph &g,char u)
{for(int i = 0; i < g.vexnum; i++){if(u == g.vexs[i]) return i;}return -1;
}int createudn(amgraph &g)
{cin >> g.vexnum >> g.arcnum;for(int i = 0; i < g.vexnum; i++){cin >> g.vexs[i];}for(int i = 0; i < g.arcnum; i++)for(int j = 0; j < g.arcnum; j++)g.arcs[i][j] = 32767;for(int k = 0; k < g.arcnum; k++){char v1,v2;int w;cin >> v1 >> v2 >> w;int i = locatevex(g,v1);int j = locatevex(g,v2);g.arcs[i][j] = w;g.arcs[j][i] = w;}return 1;
}#define mvnum 100
typedef struct arcnode{int adjvex;struct arcnode* nextarc;int info;
}arcnode;typedef struct{char data;arcnode * firstarc;
}vnode,adjlist[mvnum];typedef struct{adjlist vertices;int vexnum,arcnum;
}algraph;int createudg(algraph &g)
{cin >> g.vexnum >> g.arcnum;for(int i = 1; i <= g.vexnum; i++){cin >> g.vertices[i].data;g.vertices[i].firstarc = NULL;}for(int k = 1; k <= g.arcnum; k++){cin >> v1 >> v2;int i = locatevex(g,v1);int j = locatevex(g,v2);arcnode *p1;p1 = new arcnode;p1 -> adjvex = j;p1 -> nextarc = g.vertices[i].firstarc;g.vertices[i].firstarc = p1;arcnode *p2;p2 = new arcnode;p2 -> adjvex = i;p2 -> nextarc = g.vertices[j].firstarc;g.vertices[j].firstarc = p2;}return 1;
}void dfs(amgraph g,int v)
{cout << v;visited[v] = true;for(int w = 0; w < g.vexnum; w++){if(g.arcs[v][w] != 0 && !visited[w]) dfs(g,w);}
}void bfs(graph g,int v)
{cout << v;visited[v] = true;initqueue(q);enqueue(q,v);while(!queueempty(q)){dequeue(q,u);}for(int w = firstadjvex(g,u); w > 0; w = nextadjvex(g,u,w)){if(!visited[w]){cout << w;visited[w] = true;enqueue(q,w);}}
}