【MATLAB第102期】基于MATLAB的BRT增强回归树多输入单输出回归预测模型
BRT,即Boosted Regression Trees(增强回归树),是一种用于回归问题的集成学习方法。它结合了多个决策树模型,通过逐步改进的方式来提高整体模型的预测性能。BRT的核心思想是利用多个弱学习器(在这个情况下是决策树)的组合来构建一个强学习器。
一、模型介绍
1、工作原理
BRT的工作原理基于提升(Boosting)策略,特别是AdaBoost(Adaptive Boosting)算法的变种。在每一轮迭代中,BRT都会执行以下步骤:
初始化数据权重分布:开始时,每个训练样本都被赋予相等的权重。
构建决策树:使用当前的数据权重分布来训练一个新的决策树。这个决策树通常是一个简单的、深度较浅的树,被称为弱学习器。
计算预测误差:评估新训练的决策树在整个数据集上的预测误差。
更新数据权重:根据预测误差,增加那些被错误分类的样本的权重,减少正确分类的样本的权重。这样,接下来的迭代将更加关注那些难以正确预测的样本。
减弱预测误差:将每个决策树的预测误差进行缩减,以防止过拟合。这通常通过一个学习率参数来控制。
累加模型预测:将新训练的决策树的预测结果与之前所有迭代中的树的预测结果相加,形成最终的模型预测。
这个过程会重复进行,直到达到预定的迭代次数或者模型性能不再显著提升。
2、特点
适应性强:BRT能够适应各种类型的数据,包括连续型和分类型变量。
处理缺失值:BRT可以处理数据中的缺失值,这在实际应用中非常有用。
提供概率输出:BRT可以输出分类问题的概率估计,而不仅仅是硬分类结果。
可解释性:虽然BRT是一个集成模型,但它的组成单元是决策树,因此相比其他集成方法如随机森林或梯度提升树,BRT的可解释性更强。
3、应用
BRT在各种回归问题中都有广泛的应用,包括但不限于:
预测房价
销售预测
能源消耗预测
生物统计学中的数据分析
优势与局限性
4、优势:
BRT通过集成多个决策树来提高预测精度。
能够处理复杂的数据集,包括非线性和高维数据。
可以自然地处理不同类型的数据,包括数值型和类别型数据。
5、局限性:
相对于单棵树或浅层模型,BRT模型可能更容易过拟合,尤其是在数据量较少的情况下。
模型的训练和预测过程可能需要较长的计算时间,特别是当树的数量较多时。
总的来说,BRT是一种强大的集成学习方法,适用于各种回归问题,并且在实际应用中表现出色。然而,为了获得最佳性能,可能需要仔细调整模型参数,并根据具体问题进行模型选择和优化。
二、代码实现
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行%% 导入数据
res = xlsread('数据集.xlsx');%% 划分训练集和测试集
temp = randperm(103);P_train = res(temp(1: 80), 1: 7)';
T_train = res(temp(1: 80), 8)';
M = size(P_train, 2);P_test = res(temp(81: end), 1: 7)';
T_test = res(temp(81: end), 8)';
N = size(P_test, 2);%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);%转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';% BRT模型参数
leafNum=50; %最大叶节点数量
treeNum=1000;%种群数
nu=0.1;%更新系数
%训练模型 %% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output)';
T_sim2 = mapminmax('reverse', t_sim2, ps_output)';%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);%% 绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
gridfigure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid%% 相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;disp(['训练集数据的R2为:', num2str(R1)])
disp(['测试集数据的R2为:', num2str(R2)])% MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 - T_test )) ./ N ;disp(['训练集数据的MAE为:', num2str(mae1)])
disp(['测试集数据的MAE为:', num2str(mae2)])% MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 - T_test ) ./ N ;disp(['训练集数据的MBE为:', num2str(mbe1)])
disp(['测试集数据的MBE为:', num2str(mbe2)])
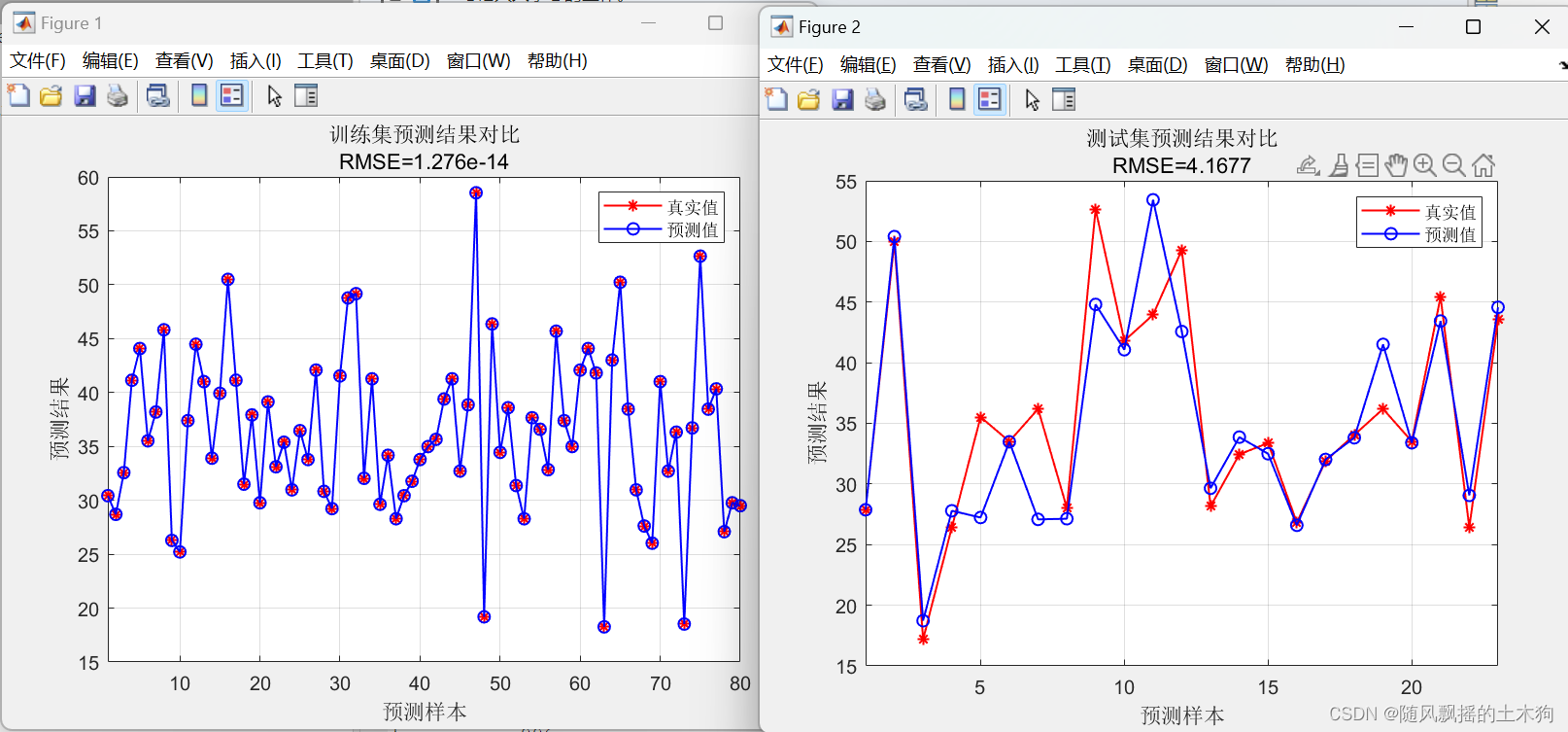
三、效果展示
四、代码获取
1.阅读首页置顶文章
2.关注CSDN
3.根据自动回复消息,回复“102期”以及相应指令,即可获取对应下载方式。
之GDAL体系架构)

)



)
)





 --- 最小公倍数、单词倒置、你是天才吗?、完美成绩、判断整数的奇偶性)

)


)
,使用内置的derby数据库,简易安装)