C++实现二叉搜索树的增删查改（非递归玩法）

文章目录

- 一、二叉搜索树的概念结构和时间复杂度
- 二、二叉搜索树的插入
- 三、二叉搜索树的查找
- 四、二叉搜索树的删除（最麻烦，情况最多，一一分析）
- - 3.1首先我们按照一般情况下写，不考虑特殊情况下
  - - 4.1.1左为空的情况（与右为空的情况差不多）
    - 4.1.2两边都不为空的情况下
  - 4.1其次我们考虑极端情况，如果刚好是整体树的根要删除
- 五、二叉搜索树的中序遍历
- 六、二叉搜索树的拷贝构造函数，析构函数，赋值操作
- - 6.1 赋值操作（比较简单）
  - 6.2拷贝构造
  - 6.3析构函数
- 七、全部源码展现（递归玩法的代码也传进来了，下次讲解）

先赞后看，养成习惯！！！^ _ ^<3 ❤️ ❤️ ❤️
码字不易，大家的支持就是我坚持下去的动力。点赞后不要忘了关注我哦！
所属专栏:C++进阶

一、二叉搜索树的概念结构和时间复杂度

二叉搜索树（Binary Search Tree）又称二叉排序树（Binary Sort Tree），是一种特殊类型的二叉树，它所有的根节点大于左子树的节点，小于右子树的节点，对二叉搜索树进行中序遍历，即可得到有序的数列。二叉搜索树的时间复杂度由树的高度决定，其搜索、插入和删除的时间复杂度均为 O(log n)，其中 n 是节点数。在最坏的情况下，仍然会有 O(n)的时间复杂度。
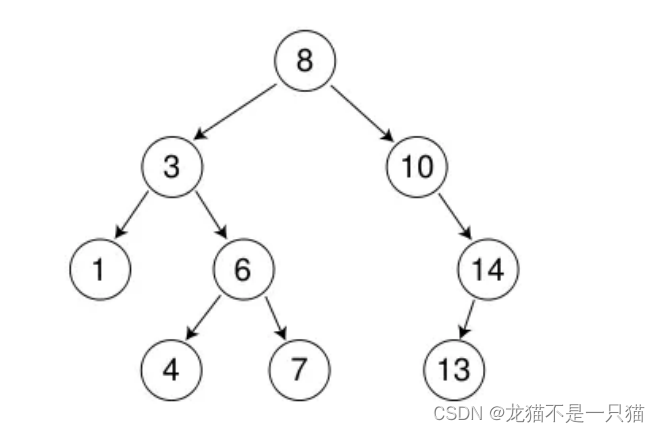
在这里插入图片描述

二、二叉搜索树的插入

首先定义一个命名空间作用域，在域中进行插入操作，构造一个二叉树的节点，对节点进行初始化构造

namespace key
{template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;BSTreeNode(const K& key):left(nullptr), right(nullptr),_key(key){}Node* left;Node* right;K _key;};template<class K>class BSTree{public:bool Insert(const K& key){Node* root = new Node(key);if (_root == nullptr){_root = root;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > root->_key){parent = cur;cur = cur->left;}else if (cur->_key < root->_key){parent = cur;cur = cur->right;}else{return false;}}if (parent->_key < root->_key)parent->right = root;elseparent->left = root;return true;}
}

代码图解：
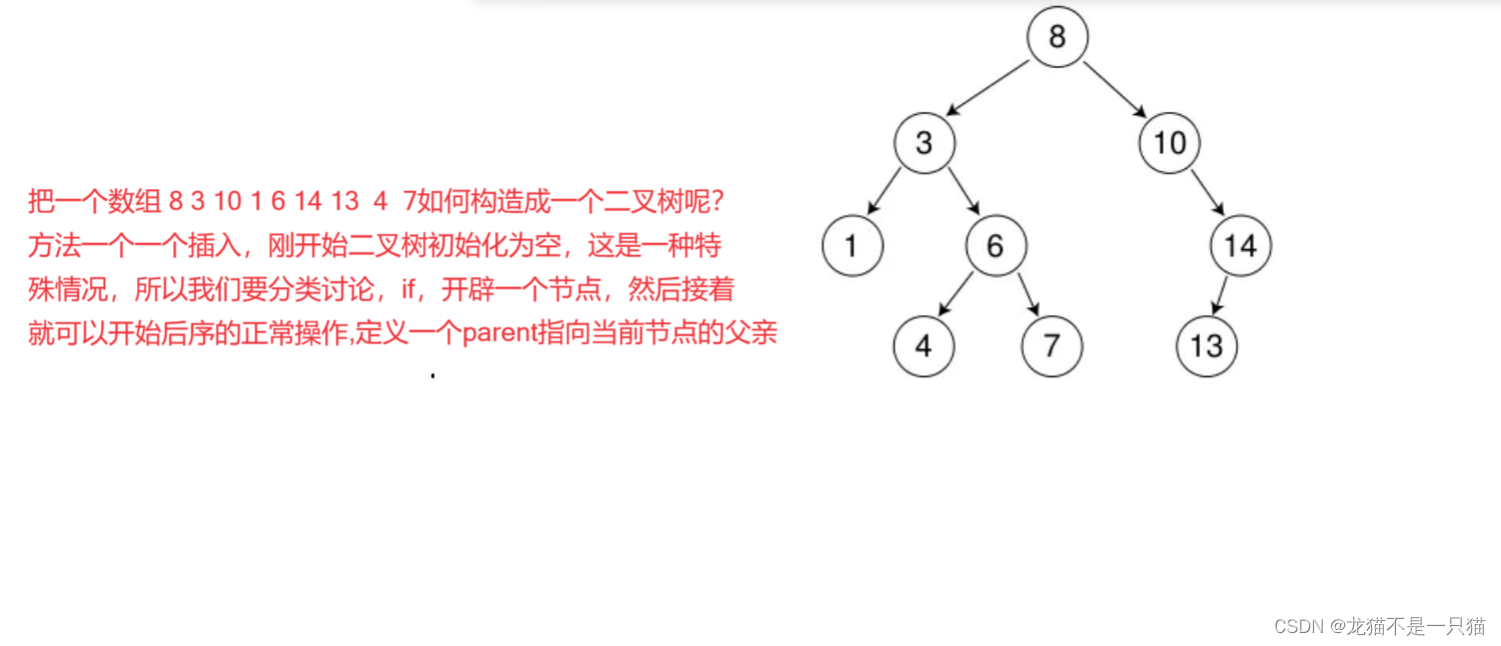
在这里插入图片描述

三、二叉搜索树的查找

查找非常简单按照流程找就行了

typedef BSTreeNode<K> Node;
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->right;}else if (cur->_key > key){cur = cur->left;}else{return true;}}return false;
}

四、二叉搜索树的删除（最麻烦，情况最多，一一分析）

3.1首先我们按照一般情况下写，不考虑特殊情况下

bool Erase(const K& key)
{assert(_root);Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->left;}else if (cur->_key < key){parent = cur;cur = cur->right;}else{if (cur->left == nullptr){if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}delete cur;return true;}else if (cur->right == nullptr){if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}delete cur;return true;}else{Node* pminleft = cur;Node* minleft = cur->right;while (minleft->left){pminleft = minleft;minleft = minleft->left;}cur->_key = minleft -> _key;if (minleft == pminleft->left)pminleft->left = minleft->right;elsepminleft->right = minleft->right;delete minleft;return true;}}}return false;
}

代码图解（解释找到时候的情况）

4.1.1左为空的情况（与右为空的情况差不多）

在这里插入图片描述

4.1.2两边都不为空的情况下

在这里插入图片描述

4.1其次我们考虑极端情况，如果刚好是整体树的根要删除

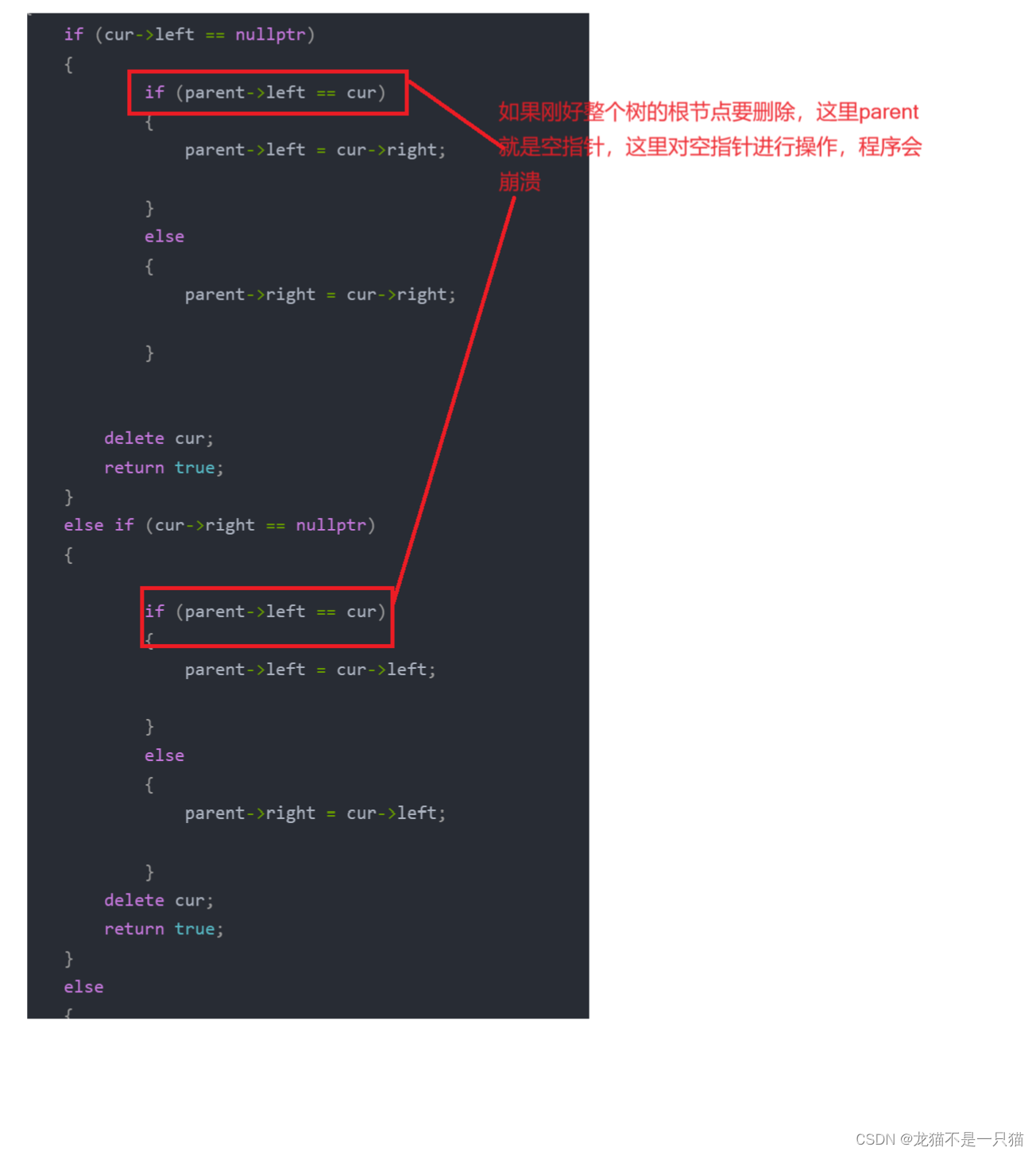
在这里插入图片描述
调整代码如下

				if (cur->left == nullptr){if (cur == _root){_root = cur->right;}else{if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}}delete cur;return true;}else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}}delete cur;return true;
}

五、二叉搜索树的中序遍历

这里我们用了一个小技巧，就是通过类里面的函数调用类里面的私有成员

//中序遍历
void _Inorder()
{Inorder(_root);
}
private://中序遍历void Inorder(Node* root){if (root == nullptr)return;Inorder(root->left);cout << root->_key << ' ';Inorder(root->right);}Node* _root = nullptr;

六、二叉搜索树的拷贝构造函数，析构函数，赋值操作

6.1 赋值操作（比较简单）

BSTree<K>& operator=(const BSTree& root)
{swap(_root, root->_root);return *this;
}

6.2拷贝构造

BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}
Node* Copy(Node* root)
{if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->left = Copy(root->left);newroot->right = Copy(root->right);return newroot;
}

6.3析构函数

~BSTree()
{Distroy(_root);
}
void Distroy(Node* root)
{if (root == nullptr)return;Distroy(root->left);Distroy(root->right);delete root;
}

七、全部源码展现（递归玩法的代码也传进来了，下次讲解）

#pragma once
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;namespace key
{template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;BSTreeNode(const K& key):left(nullptr), right(nullptr),_key(key){}Node* left;Node* right;K _key;};template<class K>class BSTree{public://查BSTree() = default;//自动生成默认构造~BSTree(){Distroy(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(const BSTree& root){swap(_root, root->_root);return *this;}typedef BSTreeNode<K> Node;bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->right;}else if (cur->_key > key){cur = cur->left;}else{return true;}}return false;}//增bool Insert(const K& key){Node* root = new Node(key);if (_root == nullptr){_root = root;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > root->_key){parent = cur;cur = cur->left;}else if (cur->_key < root->_key){parent = cur;cur = cur->right;}else{return false;}}if (parent->_key < root->_key)parent->right = root;elseparent->left = root;return true;}//删bool Erase(const K& key){assert(_root);Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->left;}else if (cur->_key < key){parent = cur;cur = cur->right;}else{if (cur->left == nullptr){if (cur == _root){_root = cur->right;}else{if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}}delete cur;return true;}else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}}delete cur;return true;}else{Node* pminleft = cur;Node* minleft = cur->right;while (minleft->left){pminleft = minleft;minleft = minleft->left;}cur->_key = minleft -> _key;if (minleft == pminleft->left)pminleft->left = minleft->right;elsepminleft->right = minleft->right;delete minleft;return true;}}}return false;}/		//递归玩法//增bool _InsertR(const K& key){_Insert(_root,key);}bool _EraseR(const K& key){_Erase(_root, key);}bool _FindR(const K& key){_Find(_root,key);}void Distroy(Node* root){if (root == nullptr)return;Distroy(root->left);Distroy(root->right);delete root;}//中序遍历void _Inorder(){Inorder(_root);}private://中序遍历void Inorder(Node* root){if (root == nullptr)return;Inorder(root->left);cout << root->_key << ' ';Inorder(root->right);}bool _Insert(Node*& root,const K& key){if (root == nullptr){Node* newroot = new Node(key);root = newroot;return true;}if (root->_key > key){_Insert(root->left, key);}else if (root->_key < key){_Insert(root->right, key);}elsereturn false;}Node& _Find(Node*& root, const K& key){if (root == nullptr)return nullptr;if (root->_key > key){_Find(root->left);}else if (root->_key < key){_Find(root->right);}else{return root;}}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->left = Copy(root->left);newroot->right = Copy(root->right);return newroot;}bool _Erase(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key > key){return _Erase(root->left,key);}else if(root->_key < key){return _Erase(root->right ,key);}else{Node* minright = root->right;while (minright->left)minright = minright->left;swap(root->_key,minright->_key);minright->right = minright->right;delete minright;return true;}}Node* _root = nullptr;};
}