【三十二】【算法分析与设计】深搜（2），98。验证二叉搜索树，不同方式定义递归函数，230。二叉搜索树中第 K 小的元素，257。二叉树的所有路径

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左

子树

只包含小于当前节点的数。

节点的右子树只包含大于当前节点的数。

所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

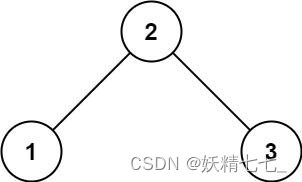
输入：root = [2，1，3] 输出：true

示例 2：

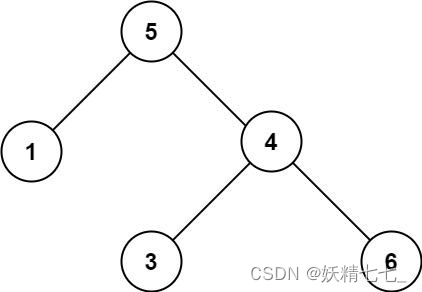
输入：root = [5，1，4，null，null，3，6] 输出：false 解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 10(4)] 内

-2(31) <= Node.val <= 2(31)1

两个递归

定义 isValidBSTHelper 递归函数，判断 root 树是否是二叉搜索树。

维护递归定义内部逻辑，左子树是二叉搜索树，右子树也是二叉搜索树，同时自身也是二叉搜索树，此时 return true。

判断左右子树是不是二叉搜索树，交给递归函数即可，我们只需要判断自身是否为二叉搜索树。

如果左子树的所有值都小于 root->val，右子树的所有值都大于 root->val，此时自身也是二叉搜索树。

递归出口，root==nullptr，return true。

定义递归函数 dfs，判断 root 树是否在范围（minVal，maxVal）之中。

维护递归定义内部逻辑，root->val 在范围内，左子树和右子树也在范围内。

递归的出口，如果 root==nullptr，return true。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:bool isValidBST(TreeNode* root) { return isValidBSTHelper(root); }private:bool isValidBSTHelper(TreeNode* node) {if (node == nullptr)return true;return isValidBSTHelper(node->left) && isValidBSTHelper(node->right) &&dfs(node->left, LONG_MIN, node->val) &&dfs(node->right, node->val, LONG_MAX);}bool dfs(TreeNode* root, long minVal, long maxVal) {if (root == nullptr)return true;if (root->val <= minVal || root->val >= maxVal)return false;return dfs(root->left, minVal, maxVal) &&dfs(root->right, minVal, maxVal);}
};

节点正确存在

另一种递归思维，定义递归函数 isValidBSTHelper 判断 node 这棵树的全部节点是否正确存在。

root 是否是二叉搜索树，取决于 root 这棵树的的所有节点是否正确存在。

维护递归的内部逻辑，node 这棵树全部节点是否正确存在，如果左子树全部节点正确存在，右子树全部节点正确存在，node 根节点也正确存在，那么就算全部正确存在。

node 根节点是否正确存在，取决于他的父亲结点，父亲节点会给予一个范围，如果在父亲结点的左子树，那么 node->val 必须小于父亲结点的 val，如果在父亲结点的右子树，那么 node->val 必须大于父亲结点的 val。

递归的出口，如果 node==nullptr，return true。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:bool isValidBST(TreeNode* root) {return isValidBSTHelper(root, LONG_MIN, LONG_MAX);}private:bool isValidBSTHelper(TreeNode* node, long minVal, long maxVal) {if (node == nullptr)return true;if (node->val <= minVal || node->val >= maxVal)return false;return isValidBSTHelper(node->left, minVal, node->val) &&isValidBSTHelper(node->right, node->val, maxVal);}
};

中序遍历有序

利用二叉搜索树的性质判断。二叉搜索树中序遍历的结果是有序序列。

root 是否是二叉搜索树，取决于 root 这棵树的中序遍历序列是否有序。

定义递归函数 isValidBST 判断 root 树中序遍历序列是否是有序序列。

定义 prev 表示前驱节点的值。

维护定义的内部逻辑，判断左子树中序遍历序列是否是有序序列，判断 root 根节点的值是否大于前驱节点的值。然后再判断右子树中序遍历序列是否是有序序列。

递归出口，如果 root==nullptr，return true。

剪枝操作，如果左子树中序遍历序列不是有序，说明 root 这棵树中序不是有序，直接返回 false。

如果 root 根节点的值小于等于前驱节点，说明 root 这棵树中序不是有序，直接返回 false。

如果右子树中序遍历序列不是有序，说明 root 这棵树中序不是有序，直接返回 false。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {long prev = LONG_MIN;public:bool isValidBST(TreeNode* root) {if (root == nullptr)return true;bool leftbool = isValidBST(root->left);if (leftbool == false)return false;bool cur = false;if (root->val > prev)cur = true;if (cur == false)return false;prev = root->val;bool rightbool = isValidBST(root->right);if (rightbool == false)return false;return true;}
};

230. 二叉搜索树中第 K 小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

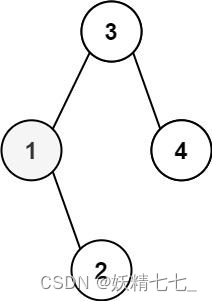
输入：root = [3，1，4，null，2]， k = 1 输出：1

示例 2：

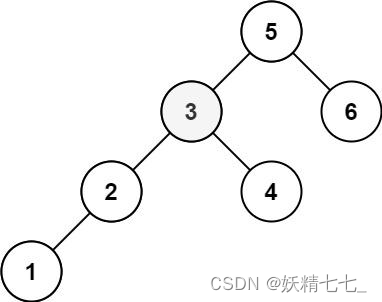
输入：root = [5，3，6，2，4，null，null，1]， k = 3 输出：3

提示：

树中的节点数为 n 。

1 <= k <= n <= 10(4)

0 <= Node.val <= 10(4)

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

二叉搜索树的性质，中序遍历序列是有序的。

定义递归函数 dfs，先遍历左子树，再遍历自己，再遍历右子树。

定义全局变量 count 和 ret，count 记录还剩需要遍历节点数量，ret 记录最终答案。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:int count;int ret;int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode* root) {if (root == nullptr)return;dfs(root->left);count--;if (count == 0)ret = root->val;dfs(root->right);return;}
};

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

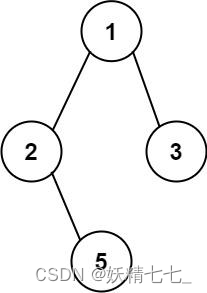
输入：root = [1，2，3，null，5] 输出：["1->2->5"，"1->3"]

示例 2：

输入：root = [1] 输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内

-100 <= Node.val <= 100

定义递归函数 dfs，将 root 这棵树的所有路径填充到 ret 中。

定义 path 存储当前节点到一开始的 root 根节点的路径。

维护递归函数的内部逻辑，首先维护 path 变量，使 path 变量存储当前节点到一开始的 root 根节点的路径。

然后再判断此时是否是叶子节点，如果会死叶子节点说明 path 是其中一个有效的路径，填充到 ret 中。

如果不是叶子节点，path 路径后面添加->。

然后将左子树路径填充到 ret 中，右子树路径填充到 ret 中。

递归出口，如果 root==0，return，此时不需要任何操作。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {// 定义dfs找到所有路径，填充到ret中// 定义path 存储当前状态路径string path;dfs(root, path);return ret;}void dfs(TreeNode* root, string path) {if (root == nullptr)return;path += to_string(root->val);if (root->left == nullptr && root->right == nullptr)ret.push_back(path);path += "->";if (root->left)dfs(root->left, path);if (root->right)dfs(root->right, path);}
};