数值稳定性
神经网络的梯度
t表示层，h^t是隐藏层，y是要优化的目标函数，不是预测还包括了损失函数
损失函数l关于参数Wt的梯度：由链式法则，损失函数l关于最后一层隐藏层求导*最后一层隐藏层对倒数第二层隐藏层求导*……
所有的h都是向量，向量关于向量的导数是矩阵，因此会出现（d-t）次矩阵乘法
这样的矩阵乘法会带来两个问题：梯度爆炸和梯度消失
举个例子：（梯度爆炸）
创建对角矩阵：当 diag 函数应用于一个向量时，它会生成一个以该向量为主对角线元素的对角矩阵，其他位置为零。
因为relu会出现0和1两种结果，所以一些元素会来自。。。
假设每个W的值都会大于1，累乘之后就会得到很大的值
e.g.梯度过大---学习率变化大，原参数-梯度乘学习率后，新的参数值会波动较大----如果参数更新过程中连续几次都以过大的步长更新，参数值可能会变得异常大，导致数值上的不稳定。这种“爆炸”效应可以迅速放大，使得参数值达到非常大的正值或负值-----如果网络中有大的参数值，它们在链式法则中相乘时会导致更大的梯度值
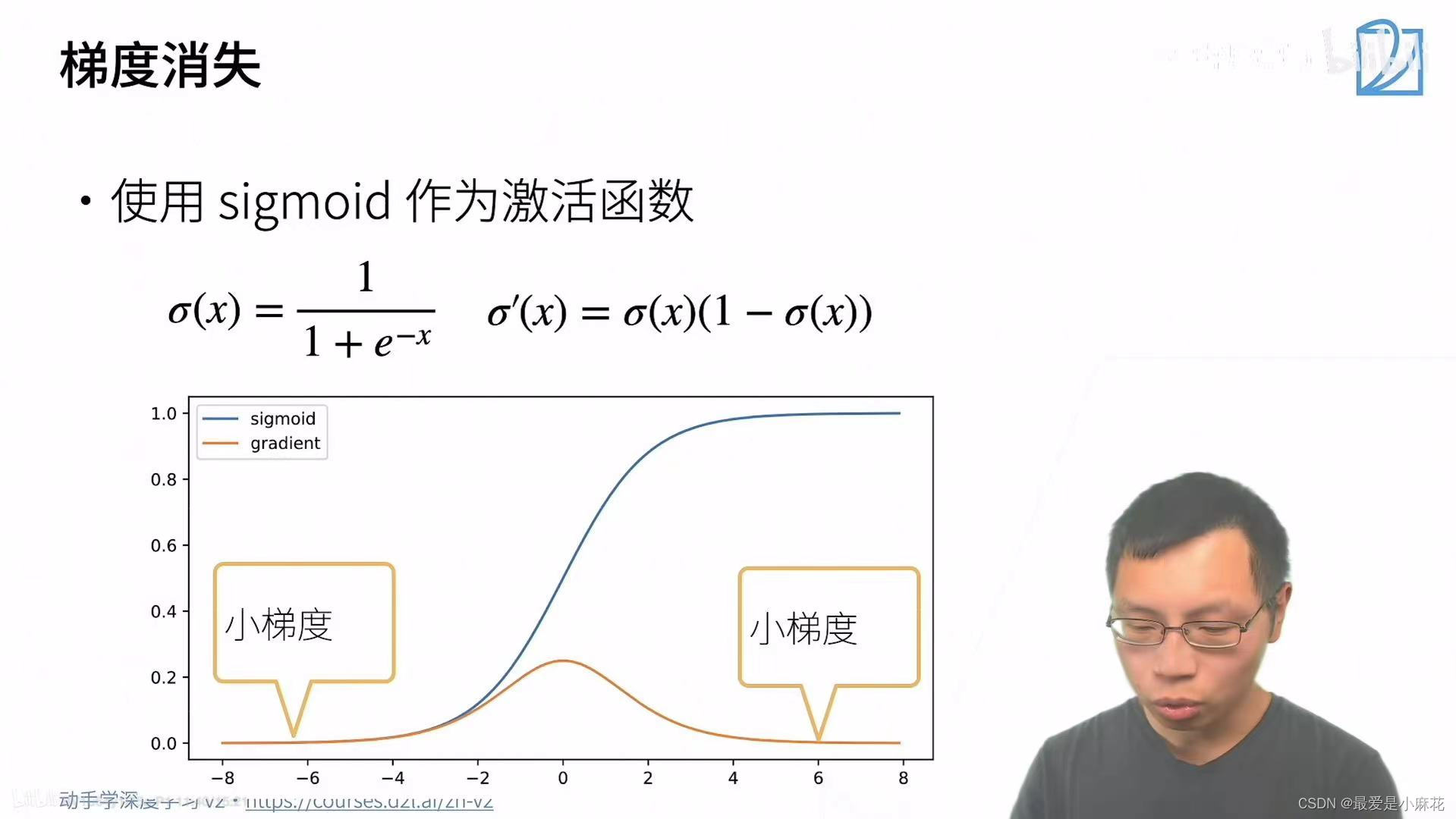
梯度消失：如果输入值大一些，sigmoid导数值就趋近于0，梯度计算就会变成极小数的累乘
对于底部尤为严重：梯度是反传的，顶部的梯度还会是正常，多层累乘过后，梯度就趋近于零
神经网络无法更深，和浅层神经网络无差别
总结：当数值（权重）过大或者过小都会导致问题
让训练更加稳定
梯度归一化：将梯度控制在均值为0，方差为1的正态分布里（控制范围）
梯度裁剪：强行把梯度减在一个范围里，比如如果梯度大于上限，就让梯度等于上限
合理的权重初始和激活函数
将每层的输出和梯度都看做随机变量，并且他们的均值和方差都保持一致，这样无论层数深度，数值都会在一定的范围内
权重初始化
在合理值区间内随机初始函数
如果在数值大的地方初始化数据，梯度就会很大
如果在最优解（较小）的地方，梯度会小
使用N（0,0.01）可能对小网络没问题，但不能保证深度神经网络
例子：MLP
假设权重是i.i.d 独立同分布
-
独立（Independent）：每个随机变量的取值不受其他随机变量取值的影响。也就是说，任意一个变量的出现都不会改变其他变量出现概率的大小。
-
同分布（Identically Distributed）：这些随机变量有着相同的概率分布。这意味着它们具有相同的概率密度函数（连续变量的情况）或概率质量函数（离散变量的情况），以及相同的期望值、方差等统计性质。
当前层的输入和当前层的权重也是独立的
假设要求输入的方差和输出的方差一致，就可以得到。。。
Xavier初始
n t-1是输入的维度，n t是输出的维度（个数），两者相等太过困难
Xavier就是折中一下取平均值为1
当输入和输出的维度有差别时，适配权重形状变换
假设线性的激活函数（理论分析，真正不可行）
式子1：已知输入h t-1的均值已经是0，输出的导数均值就是0，α*0=0，因此β=0
式子2：希望激活函数不改变输入和输出的方差，两者依然相等，因此α=1
反向同理
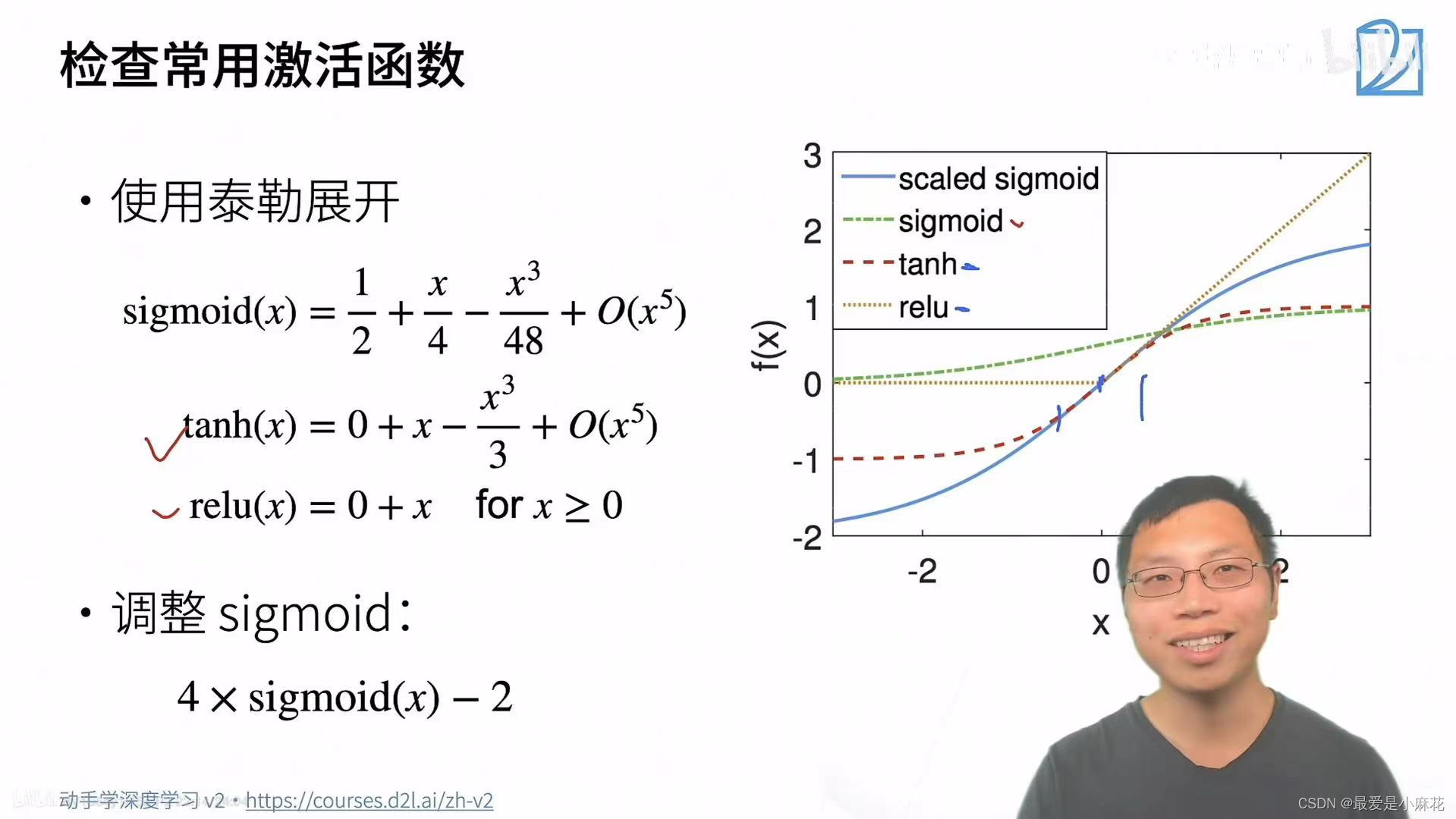
调整前的sigmoid的不符合零点
总结：合理的权重初始值和激活函数的选取可以提升数值稳定性
