
📝个人主页:五敷有你
🔥系列专栏:算法分析与设计
⛺️稳中求进,晒太阳

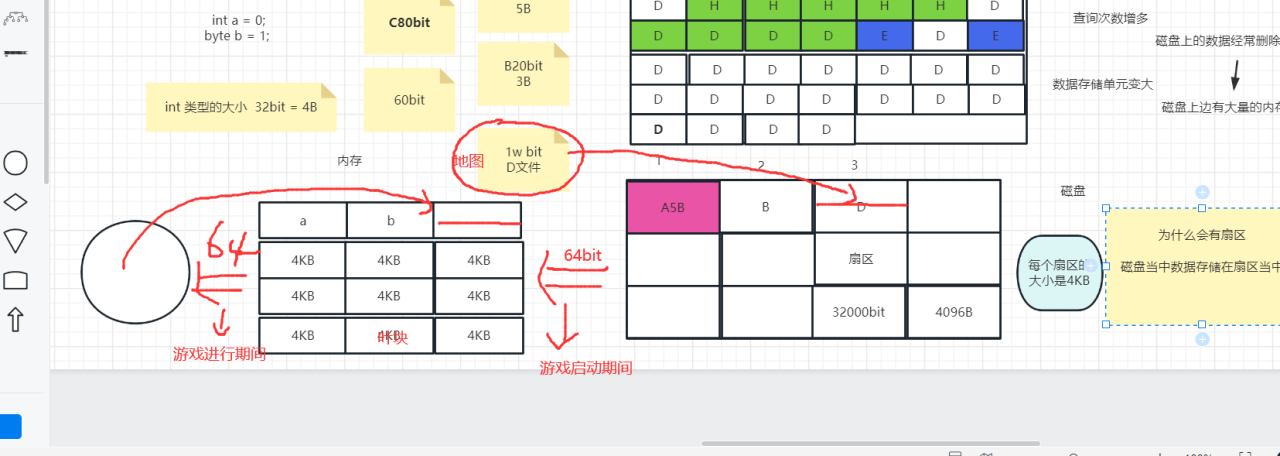
磁盘如何分配数据
数据切割:
按照固定长度进行切割---》编码翻译(常用) 计算机要求按照8bit(字节)进行切割
按照变长进行切割----》哈夫曼编码(常用于压缩)
字节是存储数据的最小单元
CPU、内存和磁盘
cpu一次处理数据(一次可以处理32bit或64bit的数据)的时间是0.2ns
磁盘查找数据需要机械臂的移动
台式机120r/s
笔记本90r/s
从cpu下达指令,到磁盘查到数据有3~6ms
内存条速度为20ns
内存的内部结构是电容器当内存条断电,数据就会消失
有中间商(内存条传输)会比原来多20ns
但时间节省在查找上
大块数据会一次性由磁盘传给内存条(游戏前的加载)
磁盘上的数据经常删除和添加--》磁盘上有大量的内存碎片----》查找次数增多

每个扇区大小是4KB(约32000bit),
内存中也有对应的叫页(内存中最基本的存储单元)
为什么要有扇区?
磁盘中数据是存储在扇区中的,是磁盘的基本单元
为什么内存用红黑树也不用b树:
b树在内存存储数据时,减少了在页间的查询次数,增加了页内的查询次数,页内查询比页间查询更耗时,所以内存使用红黑树。
为了提高查咋效率:
宁可放弃空间,也要提升查询时间
B树的应用点:
b树一般用于磁盘。
对于在内存中来说,多叉树的作用不大,但是对于磁盘来说,如果一个结点存了10个key,就可以少寻址很多次。所以多叉树的作用就是使得层高降低为了减少寻址次数。这也就是为什么磁盘的存储适合用b树或b+树的原因。
多叉树 -> 降低层高 -> 减少结点数量 -> 减少磁盘IO -> 提升性能
B+树结构特点
1.非叶子节点仅具有索引作用,也就是说,非叶子节点只能存储Key,不能存储value;2.树的所有叶节点构成一个有序链表,可以按照key排序的次序依次遍历全部数据。
B+ 树的优点
1.由于B+树在非叶子结点上不包含真正的数据,只当做索引使用,因此在内存相同的情况下,能够存放更多的key;
2.B+树的叶子结点都是相连的,因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。
B树的优点
由于B树的每一个节点都包含key和value,因此我们根据key查找value时,只需要找到key所在的位置,就能找到value,但B+树只有叶子结点存储数据,索引每一次查找,都必须一次一次,一直找到树的最大深度处,也就是叶子结点的深度,才能找到value。
未建立主键索引查询
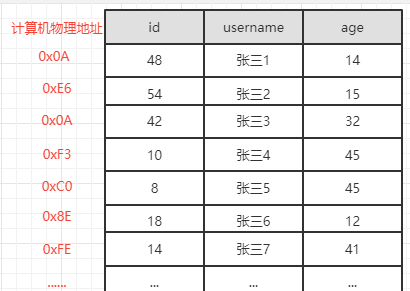
建立主键索引




)


数学表达式 数学函数 解析编译库,有效的快速和简单易用的数学和计算机的编译器)


电子科技数码爱好者交流信息新闻畅聊讨论评价)

)
)


】(工作篇)认识八大技术架构)

。)
)
