一、物理对象与形状
1.1 对象 Actor
一般来说,游戏中的对象(Actor)分为以下四类:
- 静态对象 Static Actor
- 动态对象 Dynamic Actor ---- 可能受到力/扭矩/冲量的影响
- 检测器 Trigger
- Kinematic Actor 运动学对象 ---- 忽略物理法则,由游戏逻辑直接控制(可能表现的反物理)
1.2 形状 Shape
由于真实世界中很多物体形状极其复杂,所以游戏中会先设定较为简单的对象。常见的物理对象的形状有如下:
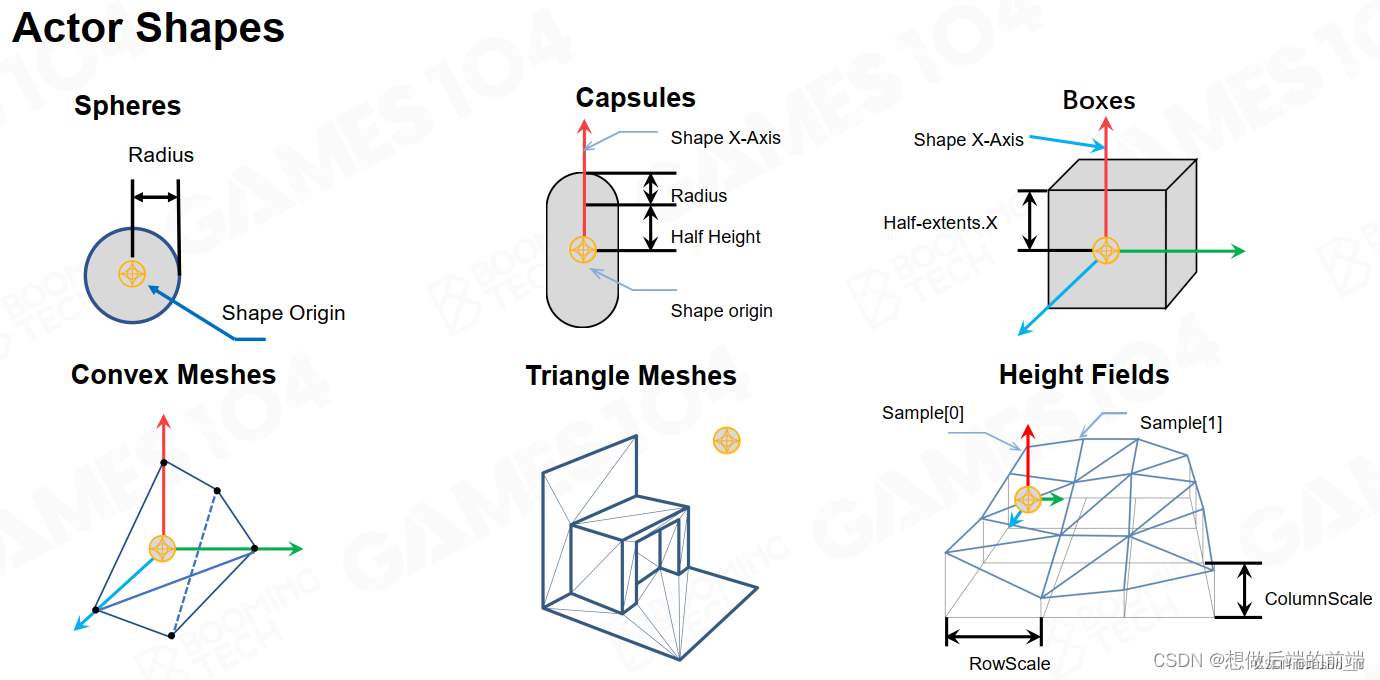
每一种形状都有常用的实际游戏对象,比如Height Fields用来做地形等。
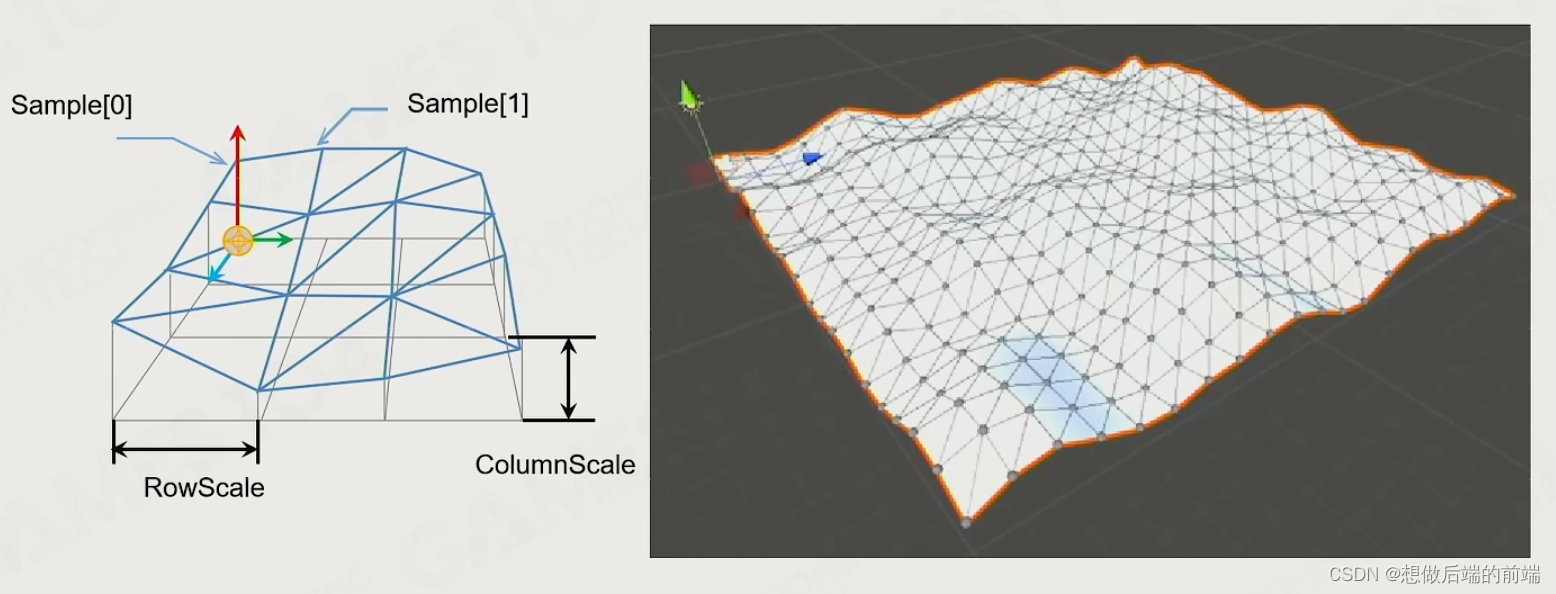
当我们利用这些对象去组成实际需要的物体对象时,有两个原则:
- 形状接近就好,不一定要完美
- 简单性。要尽量用简单的对象去拼接(比如尽量少用三角网格),且越少越好。
此外,一些比较重要的物理概念:
- 质量和密度 Mass and Density
- 质心(做载具时很重要)Center of Mass
- 摩擦和恢复(弹性) Friction & Restitution
二、 力与运动
2.1 力 Forces
一般我们把力分成两种:
- Force 可以理解为直接的重力、拉力、摩擦力等
- Impulse 冲量,比如说爆炸导致的冲击力等(虽然其实冲量就是力x时间(恒力条件下))
2.2 运动 Movement
经典的定理(游戏中需要用数学表示):
牛顿第一定律 无外力 —> 匀速直线运动
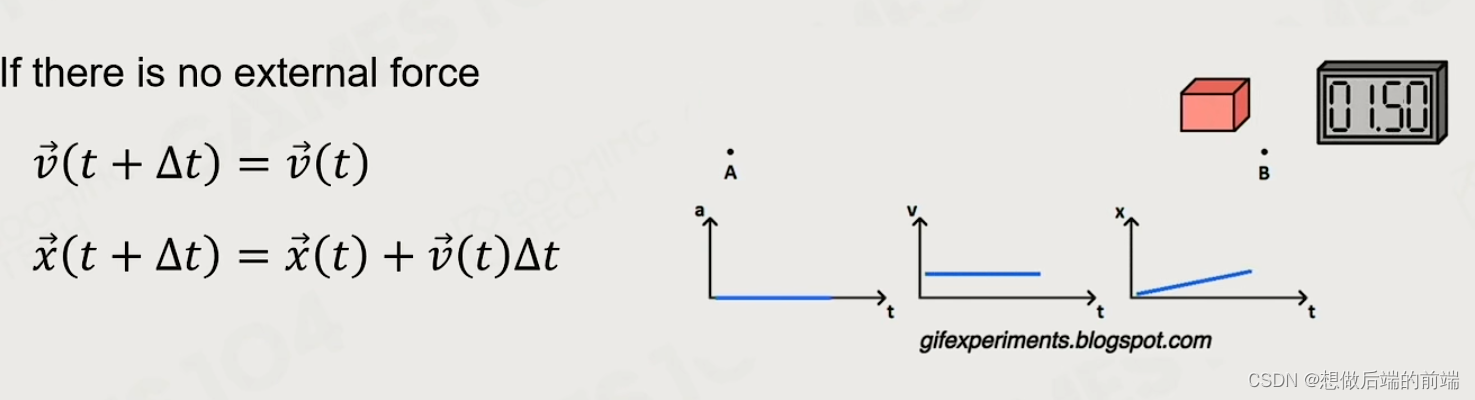
牛顿第二定律 F = ma (质量的本质是改变物体物理状态的倾向性)
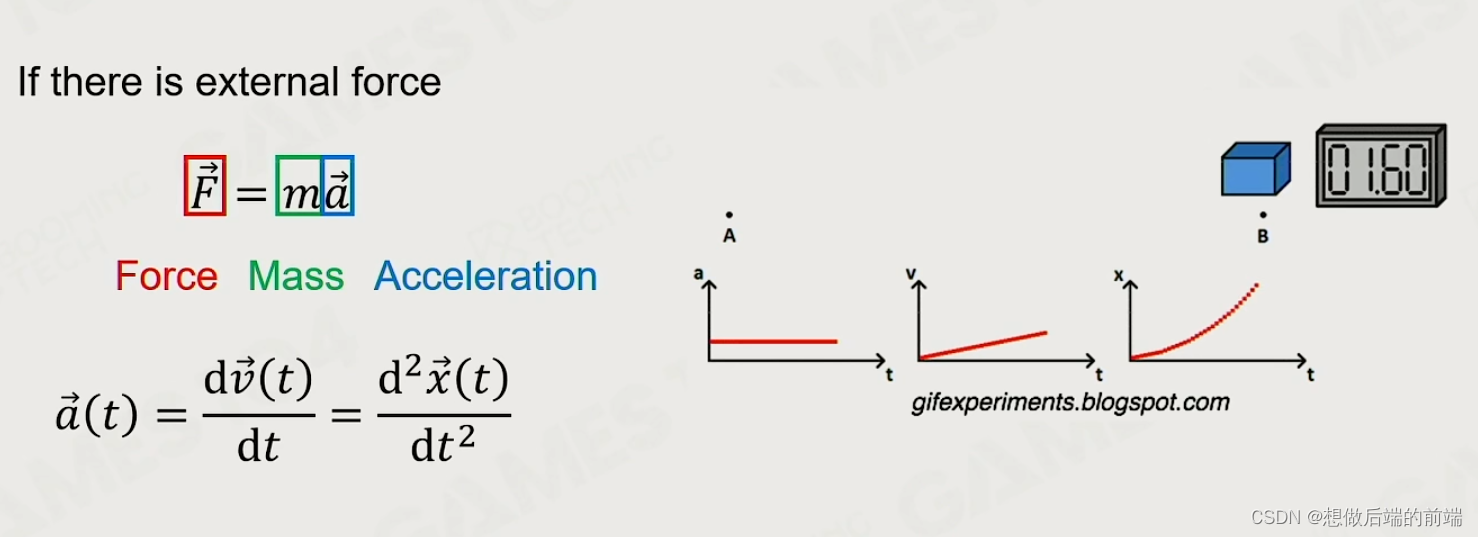
当这个力是恒力时:
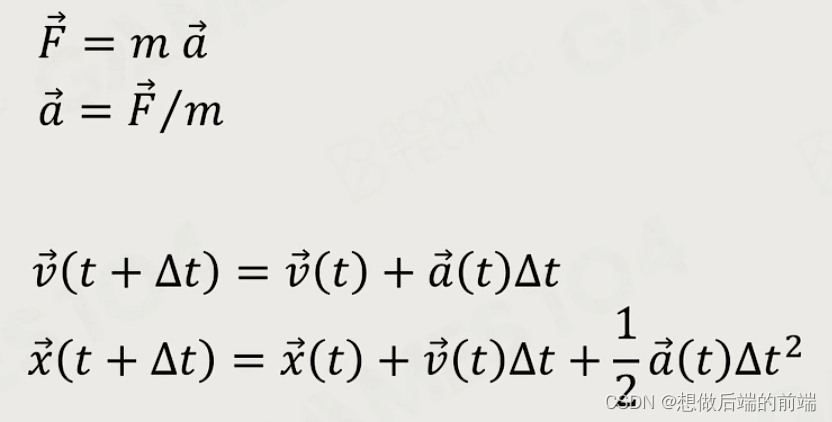
当这个力是变力时:
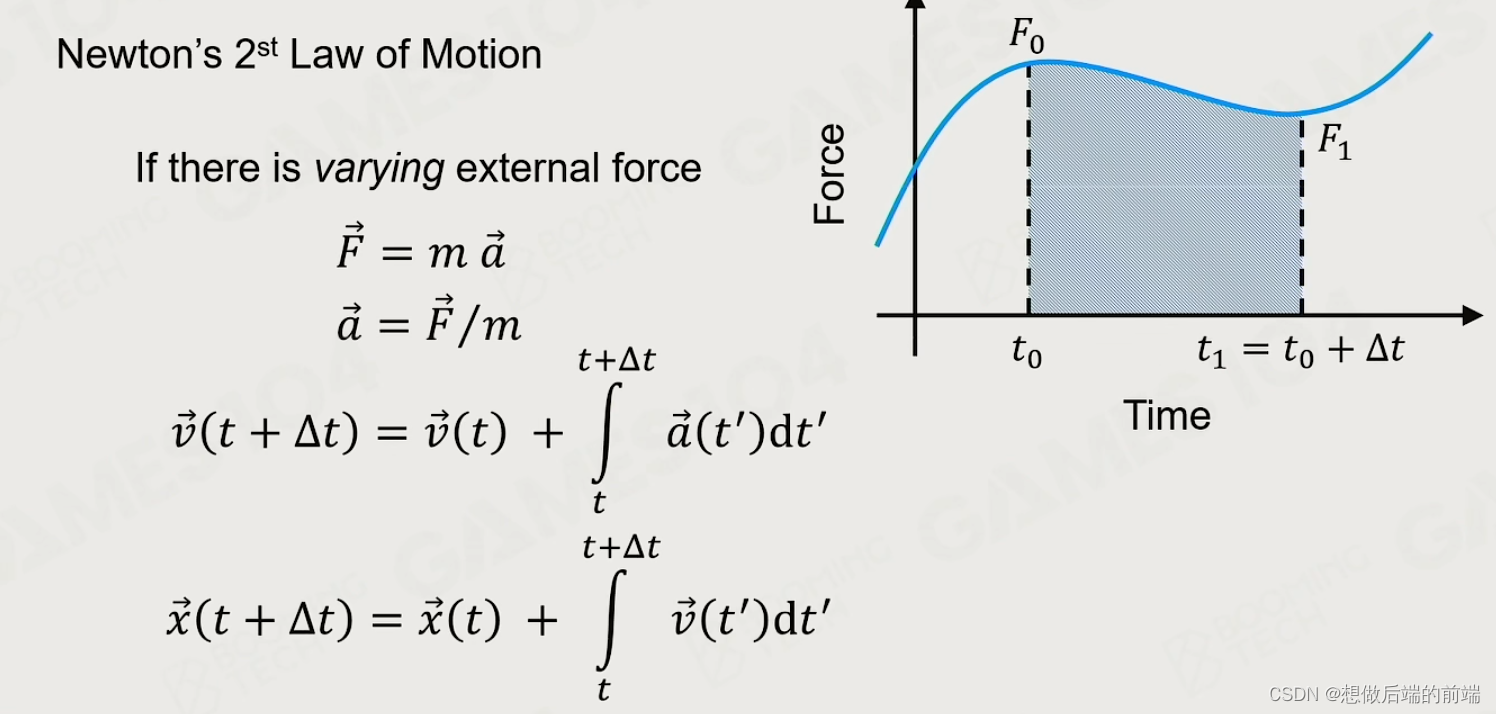
其中上图中 v ( t ′ )中的 t 是二次积分(位移和时间关系公式就是二次的)
具体以圆周运动为例,如果简单去模拟物体随时间变化,并不是很困难。
但实际游戏中时间不是连续的,而是由一帧帧实现的,所以通常需要解决的问题是在已知当前物体位置和速度的前提下获取之后某时刻的物体位置和速度信息。

2.2.1 显示欧拉法 Explicit (Forward) Euler’s Method
最简单的估计方法,假设在这个时间片里力是恒定的
每一时刻仍按照传统的牛顿力学方法去计算:

这种方法下,由于实际游戏中的时间片Δt不可能和现实中一样小,所以会导致能量不守恒(变多)(如图中右侧所示,实际位移是偏多的),误差越来越大,物体逐渐甩出去。

2.2.2 隐式欧拉法 Implicit (Backward) Euler’s Method
与显示近似,不过将力的值和速度的值以未来(终点)为参考,如下图:
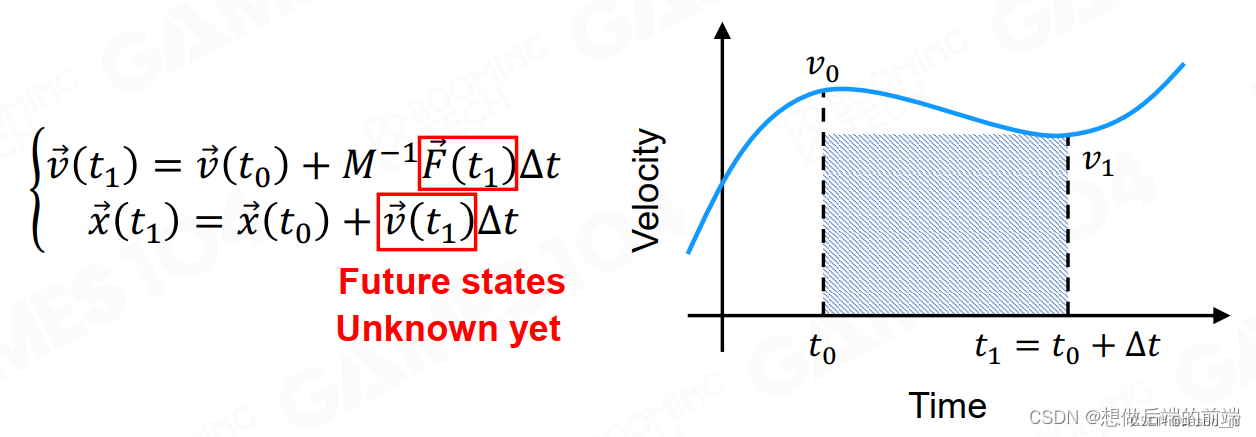
其中未来的值是假设能够通过解析解强行算出来的。
和显示方法类似,该方法的问题是能量会衰减,但由于这个衰减相对较慢,所以用户可能会认为是摩擦力、空气阻力等其他力的影响导致,从而使得这个衰减在游戏实际中相对不明显。
从另一个角度来说,我们在游戏引擎中设计中认为衰减肯定是好过增多的,前者顶多最后停下来,但后者会不可控会爆炸。
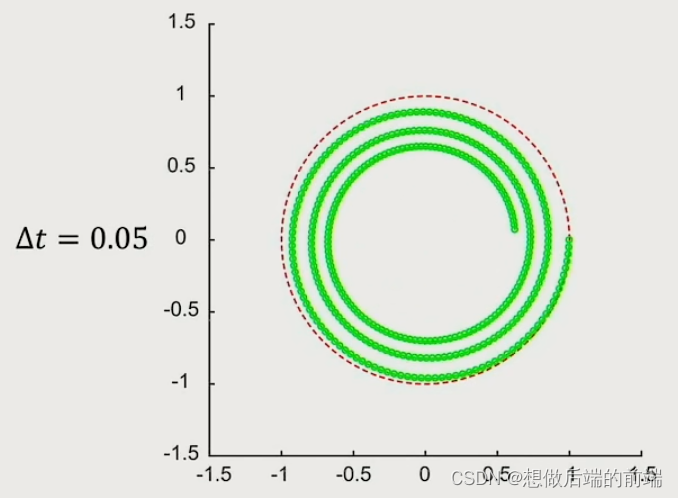
通过一系列复杂计算可以证明这种隐式方法是无条件稳定的。
但其缺点是:
- 计算成本高(计算未来值)
- 运动非线性时难以计算
- 能量衰减。
2.2.3 半隐式欧拉法 Semi-implicit Euler’s Method
综合前两者的特点:
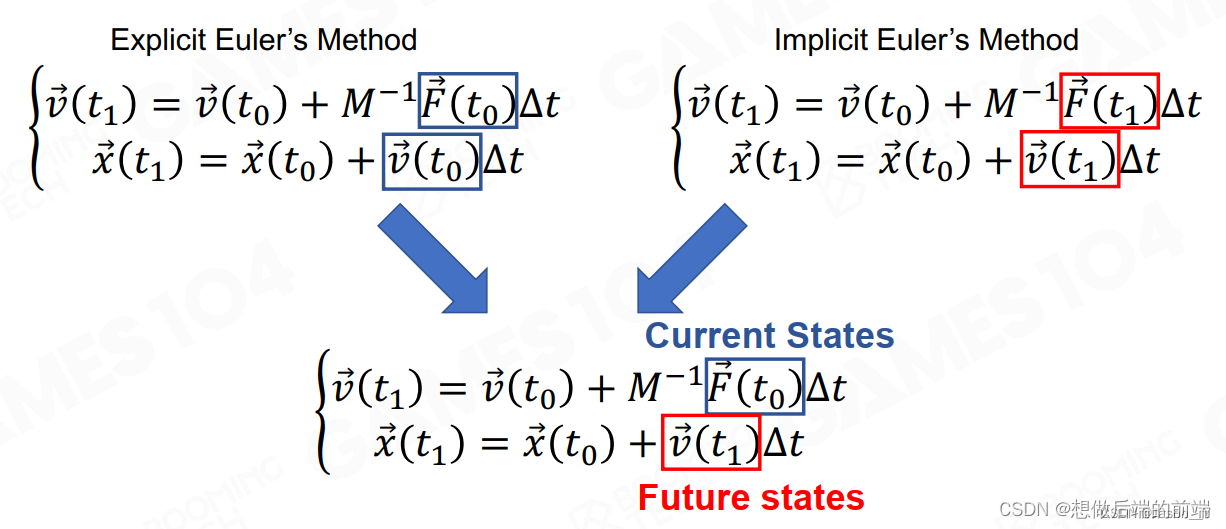
计算未来速度时用当前的力,计算未来位移时用未来的速度。

前提假设:力是不变的(很危险的假设,因为实际上力跟物体位置是相关的)。
优点是:
- 条件性稳定
- 计算简单有效
- 随着时间的推移能够保存能量
缺点是:
- 做一些sin cos等运动时,积分出来的周期会比正确值长一点点,所以在相位上会有偏移差。
三、 刚体动力学
前面所说的所有内容都是把物体看作一个质点的前提,然而事实上真实世界中大部分物体是有形状的。
一般来说,我们在引入旋转时大都针对刚体(因为柔体太难了),因为刚体就是假设物体的所有粒子之间绑定相对不动。
所以我们在刚体动力学中常常会比普通的线性计算(图中右侧)多一些概念,同一行概念有对应性:

具体相关概念建议看视频或讲义。
动量守恒:在宇宙中任意一个位置做实验的得到的结果是一样的–空间一致性
角动量守恒:在一个位置的任意一个方向做的实验得到的结果是一样的–朝向一致性
课外拓展:诺特定理
四、 碰撞检测
碰撞检测一般分为两个阶段:
- Broad phase 初筛 – 利用AABB等找到刚体有没有相交
- Narrow phase – 获取进一步信息(碰撞点、方向、深度等)
4.1 Broad Phase
一般常见的有两种方法:
BVH Tree – 更新成本低,适合动态场景。
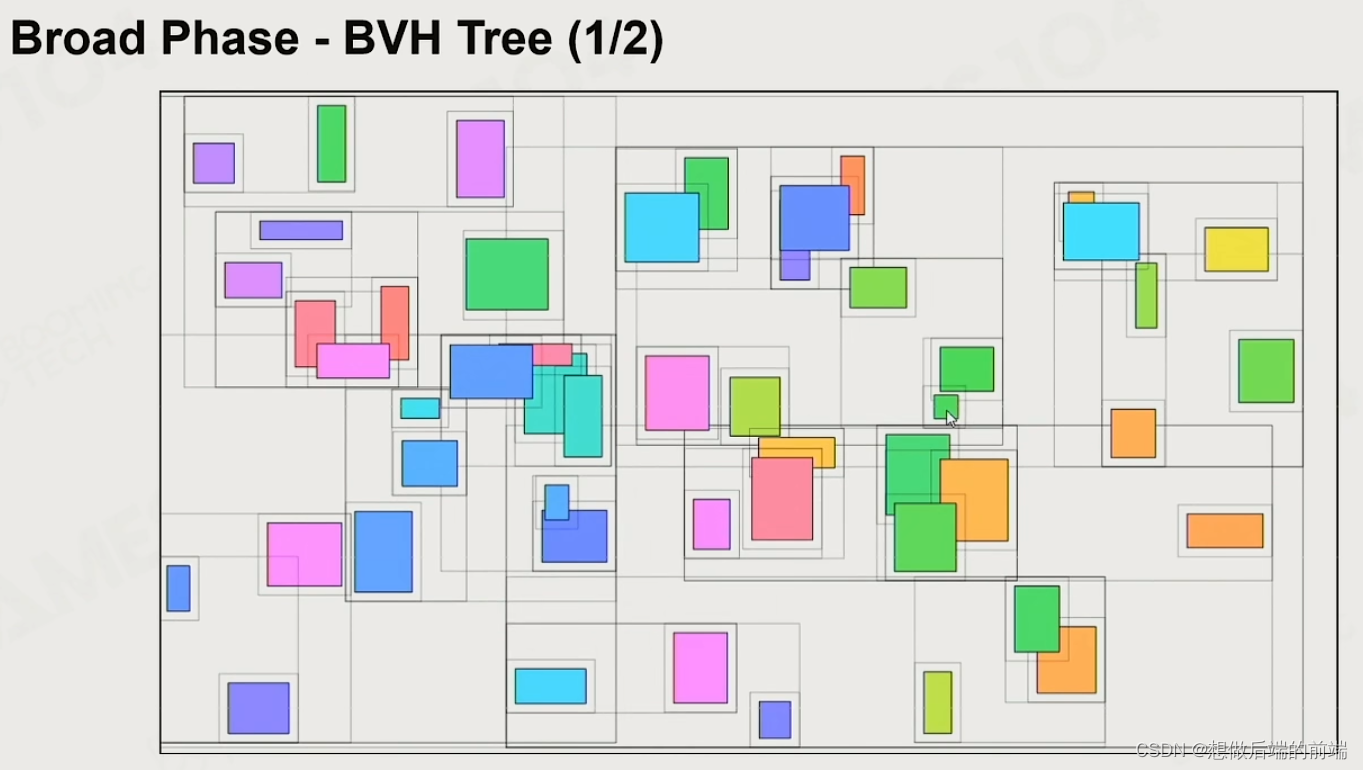
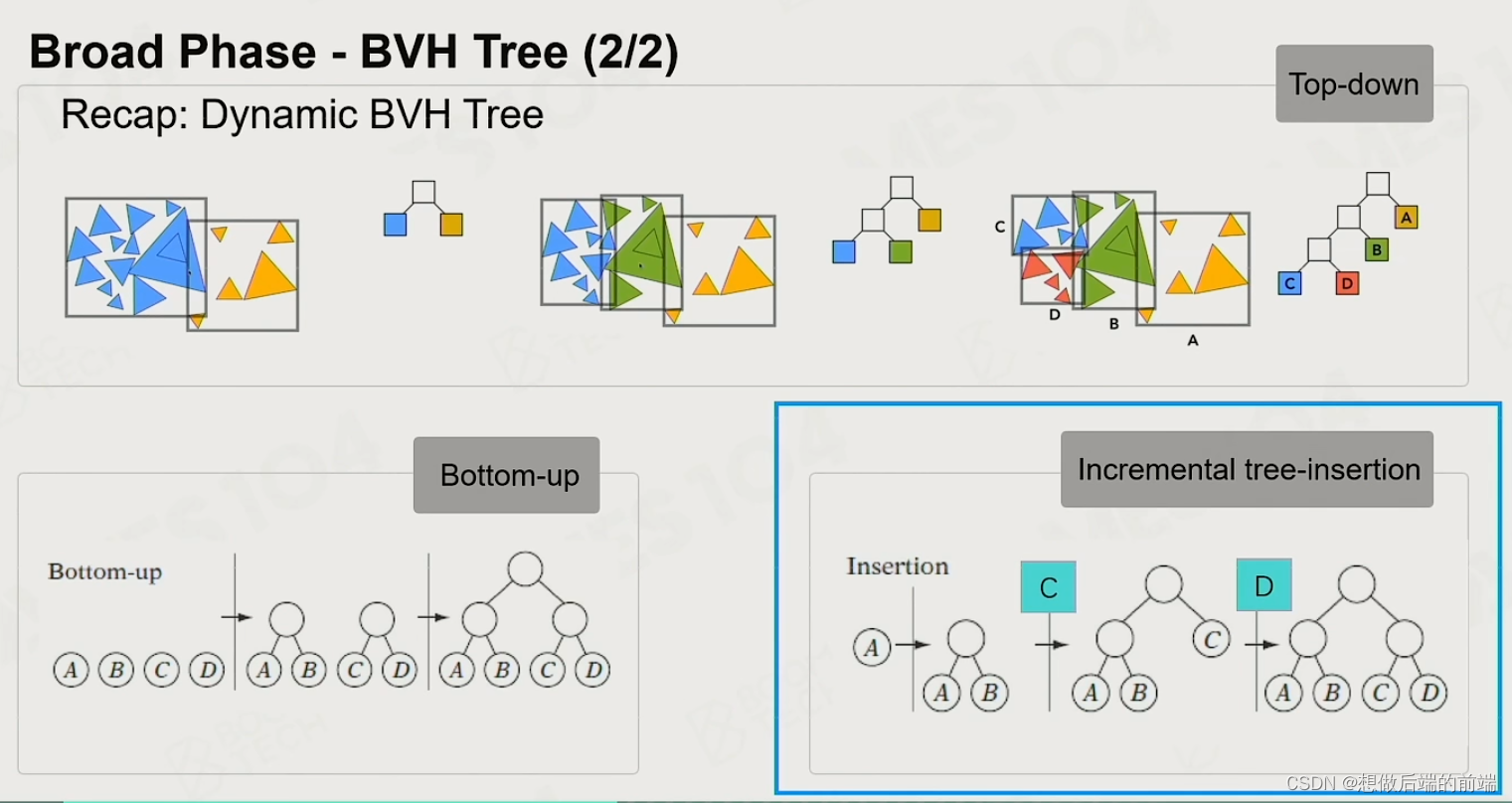
Sort and Sweep – 先排序再逐个扫描,效率高,更符合大部分为静态物体小部分为动态物体的现实。更好。
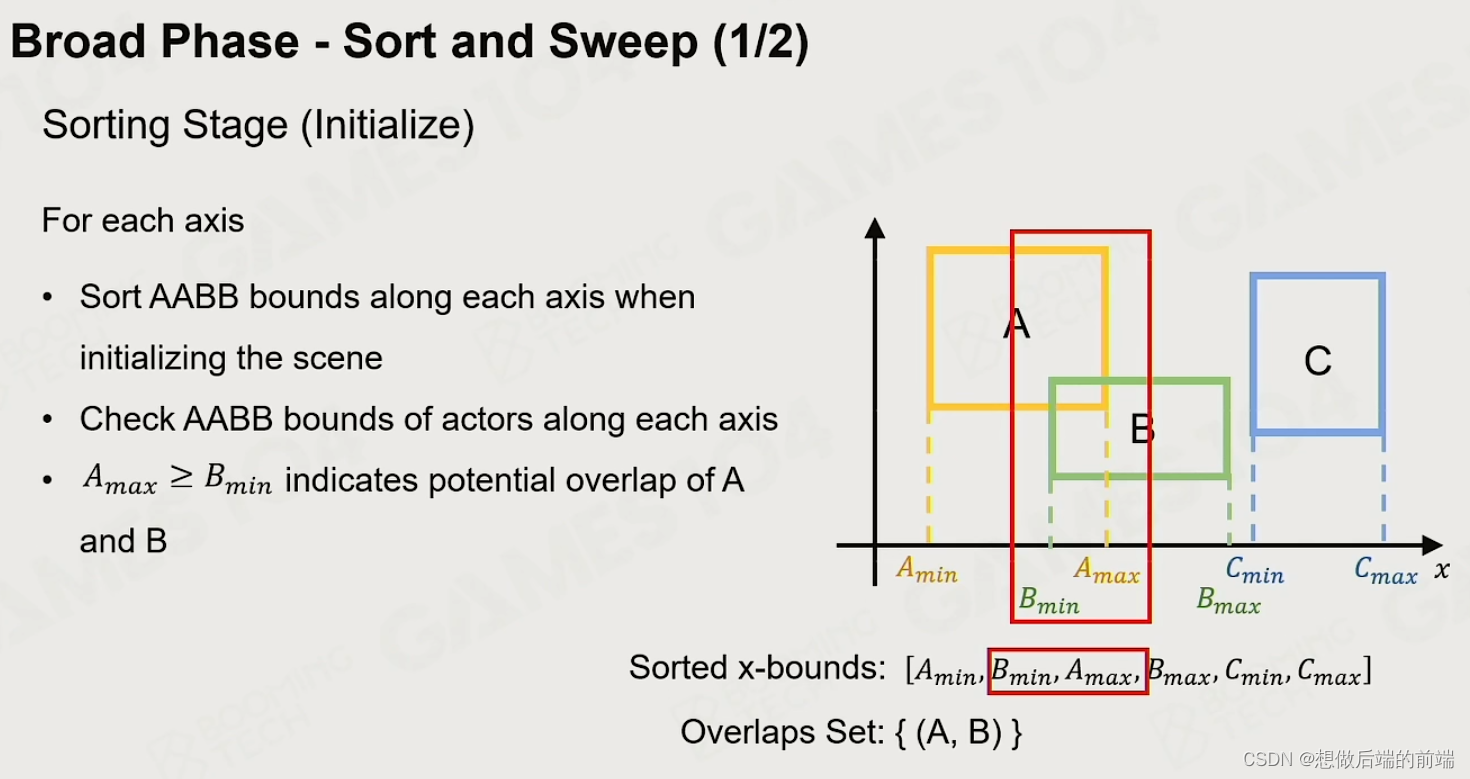
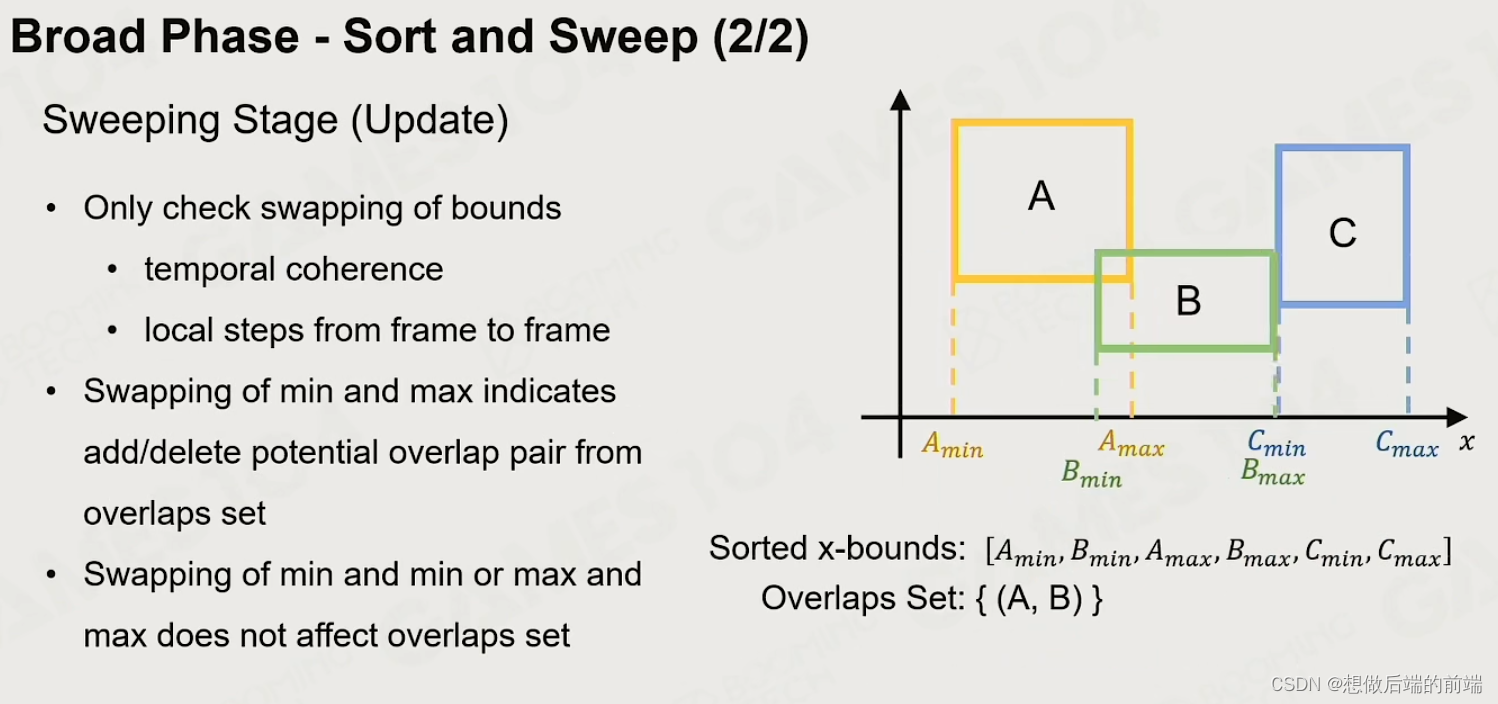
4.2 Narrow Phase
4.2.1 Basic Shape Intersection Test
比较简单,把所有物体看作球或胶囊状去判断相交即可。
4.2.2 Minkowski Difference-based Methods
首先需要知道minkowski Sum(闵可夫斯基和)的概念,以两个三角形各自围成的点集为例,两个点集相加的结果是指所有A点集的点加上所有B点集的点,几何表示如下:
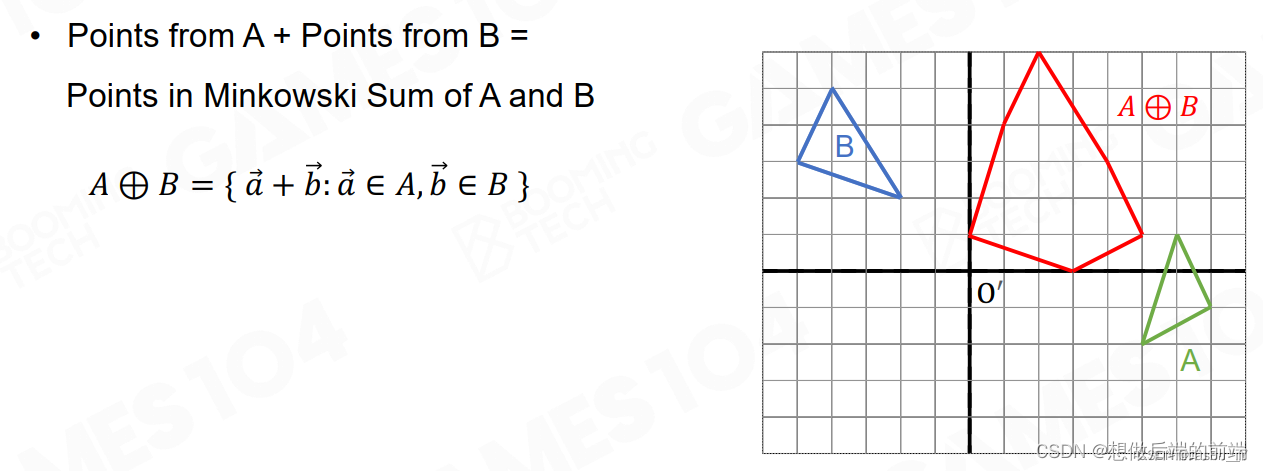
拓展到两个凸包也是一样道理。
然后同理,还有minkowski Difference(闵可夫斯基差)
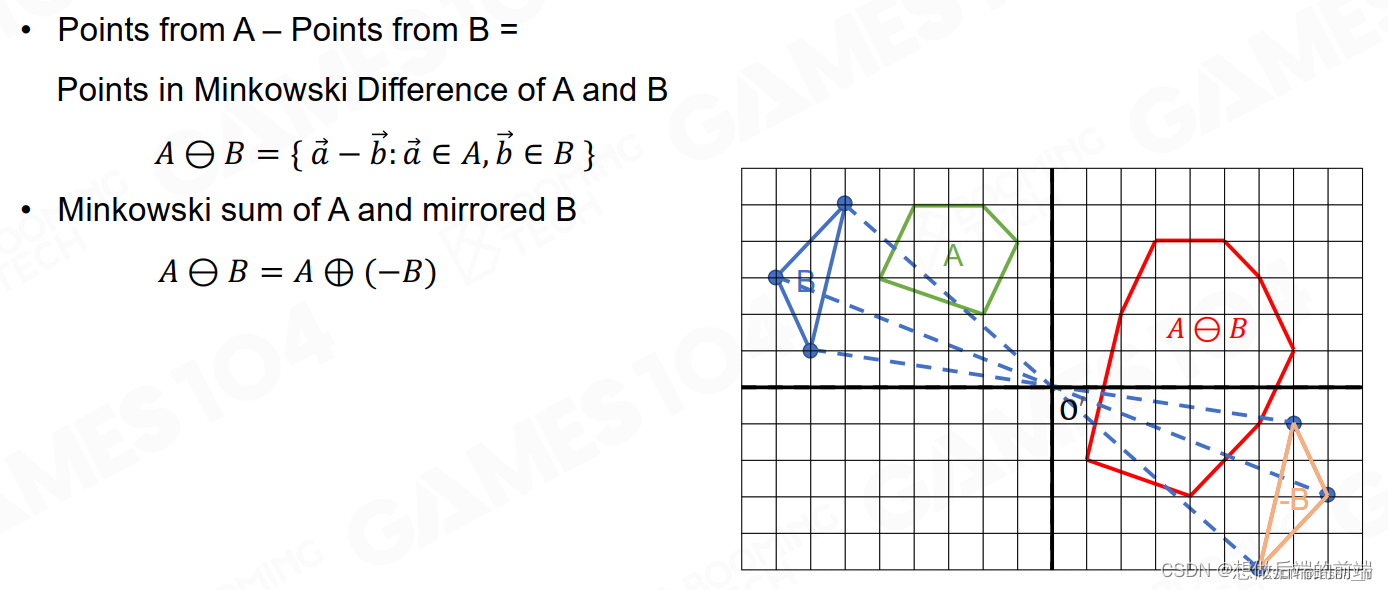
简单讲就是化A-B为A+(-B)。而-B是利用对原点的对称获得。
这样一来就获得了一个很重要的结论(方法):
如果两个凸包有重叠,则它们的闵可夫斯基差必定包含原点
我们把闵可夫斯基差这些点形成的形状叫slmplex(单纯形)
由此问题转换为了如何判断两个凸包的闵可夫斯基差包含原点。
具体可查看我的文章:多边形碰撞检测算法
4.2.3 Separating Axis Theorem
如果两个物体分离,则肯定能找到空间中一根轴把它们分隔开,不然就是相交。
简单做法是把凸包A的每条边和凸包B的每条边当分隔线试试,比如对凸包A的边a,把所有顶点投影到这条边上去进行判断有没有重叠。如果所有边做分隔线都有重叠,那就是两个凸包相交。
在这个基础上,优化方法是取凸包A的某条边a做轴时,直接将凸包B的所有顶点投影到a的垂线上,因为这样可以保证凸包A的所有顶点都在垂线上a的一侧,所以只需要判断凸包B上所有顶点在垂线上的投影是否在另一侧就行。
延伸到3D空间,需要多加步骤:
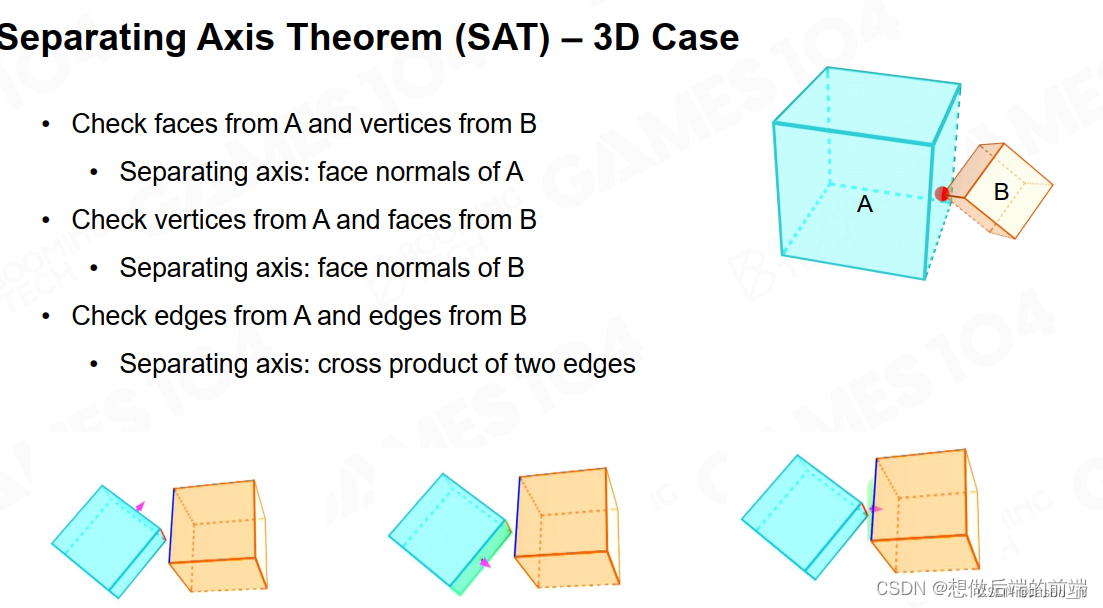
简单讲就是如果只判断面的法线作为分隔线的可行性的话,会出现图中下面前两种情况,并误以为是两个物体相交,所以需要再加上一个检测来判断第三种情况。
五、碰撞解决
如果两个物体发生了碰撞,并且相交了怎么办?
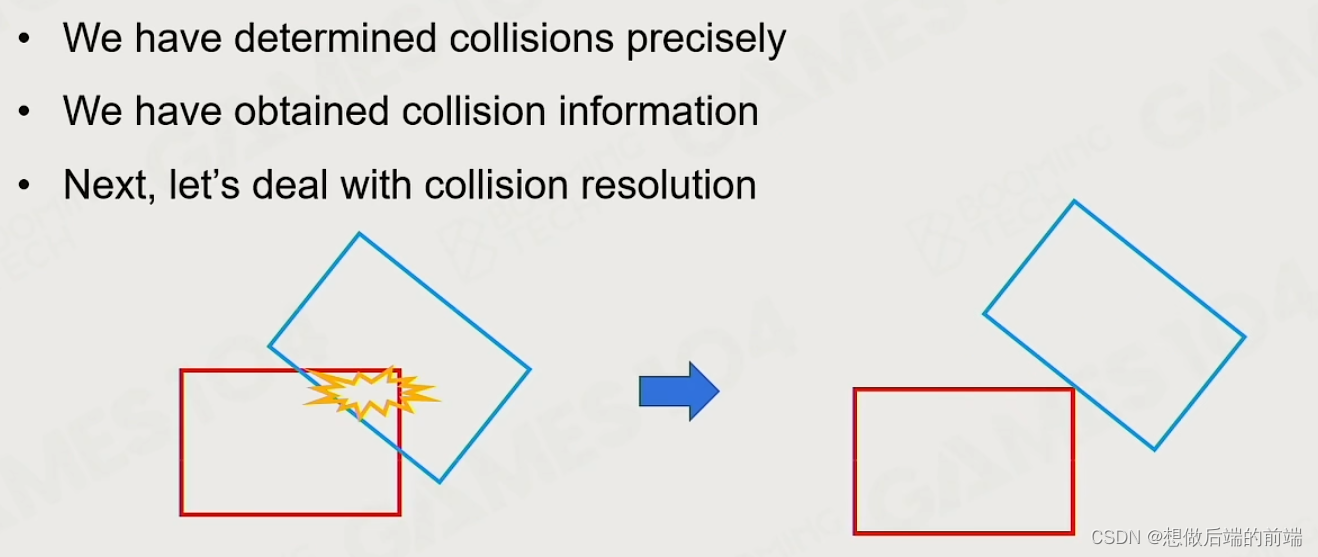
最简单的早期是方法是加一个与重叠反方向的penalty force,但是会导致物体突然分隔开,很假。
现在比较合适流行的方法是利用拉格朗日力学中对速度的约束的方法。简单讲大概类似于给碰撞物体加个冲量从而影响下速度,看是不是还碰撞,不断重复直到可以接受。或者迭代次数过多不管了。

六、 场景请求
6.1 Raycast
通过发射一条光来判断场景中的某个点能否直接看到/射击到。
当这束光有多个撞击点时,有三种处理方式:
- 都进行计算处理、
- 只处理最近的、
- any hits(不管哪个,反正有撞击就行)
6.2 Sweep
比如判断人有没有被挡住时是把人的整个胶囊体进行扫描判断的,只要有一部分被挡住就是被挡住了。
6.3 Overlap
比如判断手雷爆炸时能炸到哪些人。

七、 效率、准确性与确定性
- Sleeping
物理引擎中常把场景的不同物品或部分分成所谓不同的island,而引擎设计中很重要的一部分是让没有变化或不需要参与计算的island进入sleep,所以如何让更多island进入sleep从而减少计算量是一个关键问题。 - Continuous Collision Detection(CCD)
当一个快速运动的对象碰撞一个比较薄的物体时容易发生错误直接穿过去(因为前后两次计算时发现都没有碰撞,但其实不可以)
一种比较质朴的方法就是把墙等物体做的厚一点。
更规范的做法就是CCD:先计算一个安全时间(在这个时间内两个物体不会碰撞),然后开始一点点详细计算会不会碰撞,知道它们的距离小于一定阈值。 - Deterministic 确定性
游戏引擎设计时需要保证确定性,即同样的代码操作下跑起来是要尽可能一样的,而不会受那么多复杂计算和浮点问题的影响导致不同(从而在Online Gaming)中出现两方不一样的问题。








)


数学表达式 数学函数 解析编译库,有效的快速和简单易用的数学和计算机的编译器)


电子科技数码爱好者交流信息新闻畅聊讨论评价)

)
)

