初学双指针的同学，请先弄懂删除链表的倒数第 N 个结点。
并且在学习这一节时，不要将思维固化，认为只能这样做，这里的做法只是技巧。

一、链表相交问题

LeetCode：160.相交链表
  题目要求时间复杂度为O(L1+L2)，空间复杂度为O(1)，实际上并不是说只能遍历一次，单个链表遍历常数次，时间复杂度仍为O(L)。我们可以采用如下方法解决：

1. 计算两个链表的长度：首先遍历两个链表，计算它们各自的长度（lenA和lenB），同时检查链表的末尾节点是否相同。如果末尾节点不同，则两个链表不相交，直接返回NULL。这一步也确保了，如果两个链表相交，它们的末尾节点必定是相同的。（对于存在相交的链表，它们的的末尾结点一定是一样的！）

2. 调整起点：为了同步遍历两个链表找到交点，需要从两个链表相同的“距离”开始遍历。由于两个链表可能长度不同，我们先计算长度差abs(lenA-lenB)。然后让较长的链表的指针先前进这个长度差的步数。这样做的目的是让两个链表的指针能够在同一起跑线上“开始比赛”。

3. 同步前进直到找到交点：之后，同时前进两个链表的指针，直到它们相遇。由于步骤2已经确保了两个指针距离链表末尾的距离相同，所以它们会在交点相遇。如果两个链表有交点，那么这个交点是两个指针第一次相遇的地方。

这段代码的关键在于通过计算长度差并同步前进两个指针来找到可能的交点。这种方法不需要修改链表结构，也不需要额外的存储空间，效率较高。在最坏的情况下，时间复杂度是O(L1+L2)，其中L1和L2分别是两个链表的长度。

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {//if(!headA||!headB) return NULL;int lenA=0,lenB=0;ListNode * travelA=headA,* travelB=headB;while(travelA->next||travelB->next){if(travelA->next) {travelA=travelA->next;++lenA;}if(travelB->next) {travelB=travelB->next;++lenB;}}if(travelA!=travelB) return NULL;if(lenB>lenA) swap(headA,headB);lenA=abs(lenA-lenB);//复用for(int i=0;i<lenA;++i) headA=headA->next;while(headA!=headB){headA=headA->next;headB=headB->next;}return headA;}
};

---

---

防止大脑已经不会暴力，暴力解法：
①对于L1，从头遍历L1的每一个结点，判断该结点是否在L2中，如果在，则是相交结点。（从头遍历，第一个在的是相交结点），如果每次都遍历一次L2，则时间复杂度O(L1*L2)
②无脑的哈希优化，将L2的结点存入一个哈希表（集合），每次判断时只平均需要O(1)的时间，所以时间复杂度为O(L1+L2)，空间复杂度O(L2)。

哈希优化：

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {//if(!headA||!headB) return NULL;unordered_set<ListNode * > Set;while(headA){Set.insert(headA);headA=headA->next;}while(headB){if(Set.count(headB)) return headB;headB=headB->next;}return NULL;}
};

二、单链表判环问题

LeetCode：141.环型链表
  题目要求使用空间复杂度为O(1)，因此不能用哈希解决，用哈希只需要遍历的过程中将结点存入哈希表，每次遍历先判断该结点是否在哈希表中，如果不在则存入哈希表，如果在则找到环。但是哈希表的空间复杂度为O(L)，因此我们只能用其他方法。
  这里使用双指针，一个慢指针slow，一个快指针fast，slow一次走一步，fast一次走两步。类似于跑步比赛，从同一个长道出发，跑向运动场的跑道上跑步，由于快指针跑的速度是慢指针的两倍，快指针总会多跑一圈然后超过慢指针。
  因此如果只需要判断是否存在环只需要这样做，无环的话fast一定先跑到底：

class Solution {
public:bool hasCycle(ListNode *head) {if(!head||!head->next) return false;ListNode * slow=head;ListNode * fast=head;while(fast!=nullptr && fast->next!=nullptr){slow=slow->next;fast=fast->next->next;if(fast==slow) return true;}return false;}
};

不过，我们知道在行走时，还有信息我们没有用到，我们是否能利用这些信息找到环的入口呢？信息：

• 慢指针走的步数：step_slow，快指针走的步数：step_fast，则有step_fast=step_slow*2。
• 假设环外结点数为a，环中结点数为b，设x是fast和slow相遇时离换入口的距离，则step_fast=a+nb+x，step_slow=a+cb+x，（0<=x<b）。
• 联立可得①a+nb+x=2a+2x+2cb②nb=a+x+2cb③(n-2c)b=a+x。
• 由③可知a+x>0，且a+x是圈中结点数的倍数，换句话说，由于现在走到的位置是x，则在fast和slow相遇的位置，再走a步可以走到环的入口（因为再走这么多步刚好是环的倍数步），换句话说，如果现在有一个指针p从环外起点出发，每次走一步，与fast或slow一同行走，走完环外结点个数步（a步）之后会在环的入口处相遇！

寻找环的入口：

ListNode *detectCycle(ListNode *head) {ListNode *slow = head, *fast = head;// 第一次遍历，找到快慢指针相遇点while (fast != nullptr && fast->next != nullptr) {slow = slow->next;fast = fast->next->next;if (slow == fast) { // 发现环// 将其中一个指针（这里选择slow）移回头节点slow = head;// 两个指针以相同速度移动，再次相遇点即为环入口while (slow != fast) {slow = slow->next;fast = fast->next;}return slow; // 返回环入口}}return nullptr; // 无环
}

三、回文链表

LeetCode：234.回文链表
  回文链表，我们可以这样做，我们单独存一个原链表的反置之后的链表，然后反置的 和 原链表 从首位置开始齐步向前就行。（当然逆序的话，使用栈也是可以的！栈就相当于你存进去的东西想逆着拿出来，换句话说，你只需要逆序来查看某个东西的元素，存入栈是很好的选择！）不过时间复杂度需要的是O(1)，我们需要一点点技巧。但是单链表怎么也不可能反着遍历呀！怎么办呢？！

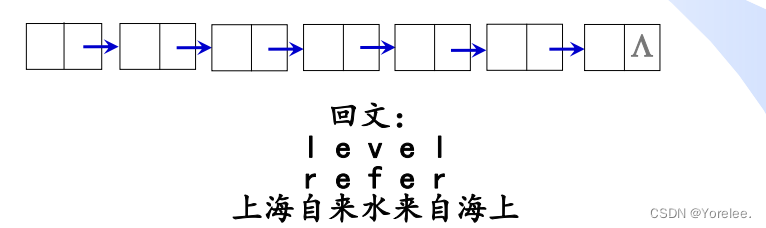
将中点之后的链表部分翻转吧朋友：找到链表中点，然后将后面的链表翻转，然后就可以首尾齐进了。翻转链表只需要O(1)的时间复杂度，三个指针~，不过如果原题说不允许修改原结构，那就再翻转过了即可（虽然输入和输出只是一个接口，但是这确实只能说很离谱）。

反转链表的后半部分：

1. 找到中点：使用快慢指针找到链表的中间节点。
2. 反转后半部分：从中间节点开始反转链表的后半部分。
3. 比较前后半部分：将前半部分和反转后的后半部分进行比较，如果每个节点的值都相同，则链表是回文。
4. 恢复链表（可选）：如果需要保持原链表的结构，可以再次反转后半部分以恢复原链表。

这种方法的空间复杂度为O(1)，但需要改变链表结构（如果不恢复的话）。

class Solution {
public:bool isPalindrome(ListNode* head) {if (head == nullptr) {return true;}// 找到前半部分链表的尾节点并反转后半部分链表ListNode* firstHalfEnd = endOfFirstHalf(head);ListNode* secondHalfStart = reverseList(firstHalfEnd->next);// 判断是否回文ListNode* p1 = head;ListNode* p2 = secondHalfStart;bool result = true;while (result && p2 != nullptr) {if (p1->val != p2->val) {result = false;}p1 = p1->next;p2 = p2->next;}        // 还原链表并返回结果firstHalfEnd->next = reverseList(secondHalfStart);return result;}ListNode* reverseList(ListNode* head) {ListNode* prev = nullptr;ListNode* curr = head;while (curr != nullptr) {ListNode* nextTemp = curr->next;curr->next = prev;prev = curr;curr = nextTemp;}return prev;}ListNode* endOfFirstHalf(ListNode* head) {ListNode* fast = head;ListNode* slow = head;while (fast->next != nullptr && fast->next->next != nullptr) {fast = fast->next->next;slow = slow->next;}return slow;}
};

四、重排链表结点

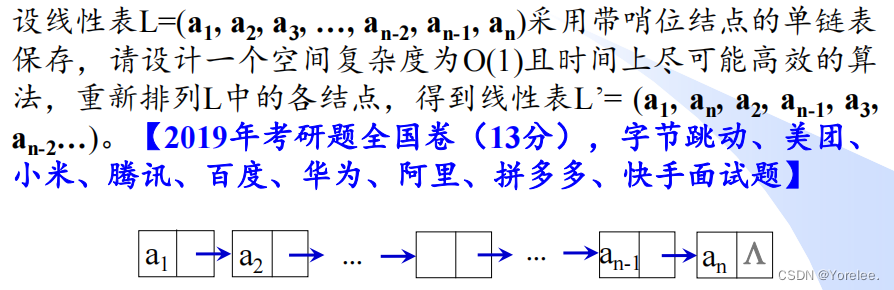
这个和回文链表是一样的，将中点之后的链表部分翻转，然后就可以一个一个选了。