大家好，我是微学AI，今天给大家介绍一下机器学习实战17-高斯朴素贝叶斯(GaussianNB)模型的实际应用，结合生活中的生动例子帮助大家理解。GaussianNB，即高斯朴素贝叶斯模型，是一种基于概率论的分类算法，广泛应用于机器学习领域。该模型假设特征之间相互独立，并且每个特征服从高斯分布（正态分布），通过学习训练数据集中的先验概率和条件概率来实现对未知数据的预测。
在模型结构上，GaussianNB主要由两部分构成：一是各类别的先验概率，通过统计训练集中各类样本的数量得到；二是给定类别条件下各特征的概率分布参数，包括均值和方差，用于描述特征符合高斯分布的情况。在实际应用中，由于其算法简单、易于理解和实现，且对于大规模数据集有较高的处理效率，GaussianNB常被用于文本分类、情感分析、疾病诊断等多个场景。然而，该模型对输入数据的独立性假设较为严格，对于非线性或者相关性强的数据拟合效果可能不佳。

一、GaussianNB模型概述

高斯朴素贝叶斯模型基本原理

GaussianNB模型，即高斯朴素贝叶斯分类器，是一种基于概率论的分类方法，其核心思想是假设特征之间相互独立，并且每个特征都服从高斯分布（正态分布）。在训练阶段，该模型会为每个类别学习一个类条件概率分布，包括每个特征均值和方差。在预测阶段，它通过计算待测样本属于各个类别的概率并选择最高概率的类别作为预测结果。

具体来说，对于给定的数据集，GaussianNB首先计算每个特征在各类别下的均值和方差，然后利用贝叶斯公式计算待分类样本属于各个类别的后验概率，即P(类别|特征)，并通过比较这些概率大小来决定样本的类别归属。

假设我们正在建立一个系统用于预测明天是否会下雨。我们收集了过去几天的三个特征数据：早晨的平均温度、湿度和云层厚度。我们可以使用GaussianNB模型，假设这三个特征彼此独立，并且各自在“下雨”和“不下雨”两种情况下的分布都是高斯分布。模型会分别计算出“下雨”和“不下雨”时这三个特征的平均值和方差。当需要预测明天是否下雨时，我们就将明天早晨的温度、湿度和云层厚度输入模型，模型会根据这些特征值计算出明天“下雨”和“不下雨”的概率，如果“下雨”的概率更高，则预测明天可能会下雨。这就是高斯朴素贝叶斯模型在实际生活中的应用。

应用场景举例

GaussianNB模型，全称为高斯朴素贝叶斯分类器，是一种基于概率论的分类算法，其核心思想是假设特征之间相互独立，并且每个特征服从高斯分布（正态分布）。在训练阶段，它会计算每个类别下各个特征的均值和方差，然后在预测阶段，利用贝叶斯定理计算待测样本属于各个类别的概率，并将其分到概率最高的类别中。

应用场景举例：

1. 文本分类：如垃圾邮件识别，通过分析邮件中的关键词出现频率等特征，利用GaussianNB模型预测邮件是否为垃圾邮件。
2. 医疗诊断：通过对病人的各种生理指标数据进行分析，如体温、血压、心率等，利用GaussianNB模型预测患者可能患有的疾病类型。
3. 信用评分：在金融领域，通过分析用户的收入、年龄、职业、贷款历史等信息，使用GaussianNB模型预测用户违约的可能性。

假设你是一位水果摊主，需要快速判断顾客手中的水果是苹果还是橙子，但只能观察重量和颜色这两个特征。经过长期观察，你知道苹果和橙子的重量分别服从某个平均值和标准差的正态分布，颜色也有特定的概率分布。这时，GaussianNB模型就像你的智能助手，当你给它提供一个水果的重量和颜色时，它就会根据之前学习到的分布规律，计算这个水果更可能是苹果还是橙子，从而帮助你快速分类。例如，如果水果重量较轻且颜色偏红，那么模型可能会告诉你这更有可能是苹果。

二、GaussianNB模型结构特点

参数估计

GaussianNB，即高斯朴素贝叶斯分类器，是一种基于概率论的分类算法，其核心思想是假设特征之间相互独立，并且每个特征都服从高斯分布（正态分布）。在模型结构上，对于每一个类别，GaussianNB都会为每个特征估计一个均值和方差，形成该类别的高斯分布参数。

在参数估计阶段，GaussianNB会计算每个类别下各个特征的均值和方差。均值代表了该特征在该类别下的典型取值，而方差则反映了数据点围绕均值分散的程度。训练过程中，模型通过遍历所有样本，对各类别下的各特征分别进行统计分析，从而得到这些参数。

假设我们正在建立一个模型来预测明天是否会下雨。我们的特征包括早晨的平均温度（Temp）、湿度（Humidity）和风速（WindSpeed）。GaussianNB模型会分别计算出晴天和雨天时这三个特征各自的均值和方差。例如，如果历史数据显示雨天时早晨的平均温度通常较低，湿度较高，风速适中，那么模型就会为“雨天”这一类别下的“温度”、“湿度”和“风速”特征估计出对应的均值和方差。当新的观测数据到来时，模型将利用这些预估的高斯分布参数，计算出明天是晴天还是雨天的概率，并以此作为预测结果。

分类决策过程

GaussianNB模型，即高斯朴素贝叶斯分类器，是一种基于概率论的分类方法。其主要特点是假设特征之间相互独立，并且每个特征都服从高斯分布（正态分布）。在决策过程中，它首先计算各个类别的先验概率，然后对每一个特征，分别计算该特征在各类别下的条件概率。对于待分类样本，通过将各个特征的条件概率相乘得到该样本属于各类别的后验概率，最后将其归到后验概率最高的类别中。

假设我们正在帮助一家水果店根据水果的颜色、大小和重量来区分苹果和橙子。GaussianNB模型就像一个聪明的助手，它首先观察大量已知种类的水果，统计出苹果和橙子各自出现的比例（先验概率）。然后，它发现苹果的颜色、大小和重量各自都有一个大致的正态分布范围。当有新的未知水果到来时，助手会分别测量其颜色、大小和重量，看这三个特征分别更接近苹果还是橙子的概率分布，然后将这三个概率相乘得到该水果是苹果或橙子的总概率（后验概率），并最终判断它是苹果还是橙子。这就是GaussianNB模型的决策过程。

三、GaussianNB模型实际应用案例

新闻分类任务

在新闻分类任务中，GaussianNB（高斯朴素贝叶斯）模型是一种常用的机器学习算法。该模型基于朴素贝叶斯理论，假设特征之间相互独立，并且每个特征服从高斯分布（正态分布）。具体应用时，首先对训练集中的新闻数据进行预处理，包括文本清洗、分词、提取关键词等步骤，将文本信息转化为数值型特征向量。然后利用GaussianNB模型对这些特征向量进行学习，得到各类新闻的特征分布参数。

例如，在一个在线新闻平台中，我们想要自动分类新闻为体育、科技或娱乐类别。每篇新闻都可以看作是一个“包裹”，其中包含多个“物品”（如关键词、作者、发布时间等特征）。GaussianNB模型就像一位快递员，他通过学习过往“包裹”的内容和对应标签，了解了各类新闻的特征规律。比如，如果“篮球”、“足球”等关键词常出现在体育类新闻中，而“AI”、“5G”等词更常见于科技类新闻，那么当收到新的“包裹”时，模型就能根据其中“物品”的组合情况，快速判断这篇新闻最可能属于哪个类别，从而实现自动化分类。

信用评分系统

在信用评分系统中，GaussianNB（高斯朴素贝叶斯）模型是一种广泛应用的机器学习算法。该模型基于朴素贝叶斯理论，假设特征之间相互独立，并且每个特征都服从高斯分布（正态分布）。在信用评估场景下，我们可能拥有一系列用户数据，如年龄、收入、贷款历史、信用卡欠款额度等。

例如，某银行正在构建一个自动化的信用评分系统以决定是否给申请人发放贷款以及确定贷款额度。通过收集大量用户的信用数据，并利用GaussianNB模型进行训练，模型会学习到各个特征与信用好坏之间的关系及其概率分布。

具体来说，模型会计算“年龄为30岁、年收入10万、无贷款历史、信用卡欠款5000元”的用户违约的概率是多少。在预测阶段，新申请人的信息输入模型后，模型将依据学习到的概率分布和其他申请人违约的历史情况，给出该申请人信用风险的评分。

假设你是一位水果摊主，你在过去的经验中发现，购买苹果的人群中，年轻人更倾向于选择红苹果，而年纪稍大的人更喜欢青苹果。此外，收入较高的人群购买大苹果的可能性更大。于是，当你面对一位新的顾客时，你会根据他的年龄和外表判断其可能的购买喜好（红苹果或青苹果），这就是朴素贝叶斯分类器在现实生活中的应用。而在信用评分系统中，GaussianNB模型就是那位“水果摊主”，它通过学习各种特征与信用表现的关系，来预测新申请人的信用风险。

四、GaussianNB模型的数学原理

在机器学习中，Gaussian Naive Bayes (GaussianNB) 模型是一种基于贝叶斯定理和高斯分布的概率分类器。其核心思想是假设特征之间相互独立，并且每个特征都服从高斯分布（正态分布）。以下是GaussianNB模型的数学原理：

对于给定的数据集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中$x_i\in {\mathbb{R}}^d$ 是一个d维特征向量， y i ∈ { C 1 , C 2 , . . . , C k } y_i \in \{C_1, C_2, ..., C_k\} yi​∈{C1​,C2​,...,Ck​} 是对应的类别标签。

对于每一个类别 $C_j$，GaussianNB模型假设每个特征 $x_{ij}$ 都独立地服从高斯分布：

$$p(x_{ij}|y=C_j)=\frac{1}{\sqrt{2\pi {\sigma }_j^2}}\exp \left(-\frac{(x_{ij}-{\mu }_j{)}^2}{2{\sigma }_j^2}\right)$$

其中，${\mu }_j$ 是类别 $C_j$ 对应的第i个特征的均值，${\sigma }_j^2$ 是类别 $C_j$ 对应的第i个特征的方差。

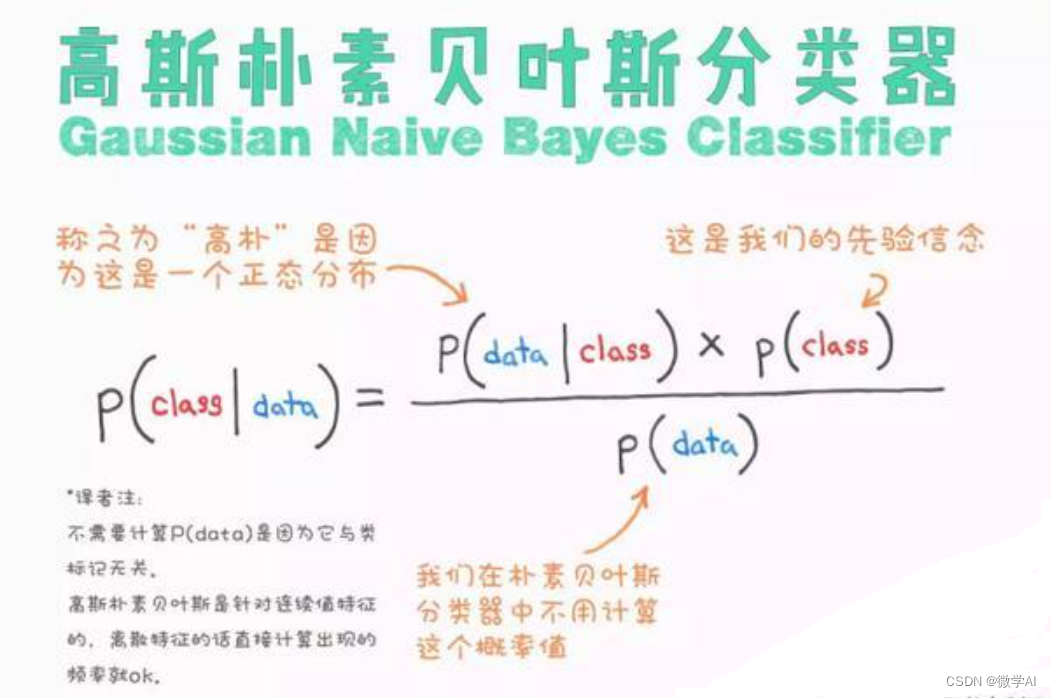
在预测阶段，利用贝叶斯定理计算后验概率：

$$P(y=C_j|x)=\frac{P(y=C_j){\prod }_{i=1}^{d}P(x_i|y=C_j)}{{\sum }_{l=1}^{k}P(y=C_l){\prod }_{i=1}^{d}P(x_i|y=C_l)}$$

其中，$P(y=C_j)$ 是先验概率，可以通过训练数据集中各类别的频率估计得到。 模型将预测使得后验概率最大的类别作为新的观测样本的类别。

五、GaussianNB模型的代码实现

在PyTorch中，Gaussian Naive Bayes (GaussianNB) 模型并不是一个内置模型，因为PyTorch主要关注神经网络和深度学习。然而，你可以基于sklearn的GaussianNB实现自行构建一个简单的版本。以下是一个使用numpy和sklearn GaussianNB的示例，然后我们将数据转换为PyTorch tensors进行处理：

import numpy as np
from sklearn.naive_bayes import GaussianNB
import torch# 假设我们有如下数据
X_train = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y_train = np.array([0, 0, 1, 1])# 使用sklearn的GaussianNB训练模型
gnb = GaussianNB()
gnb.fit(X_train, y_train)# 定义一个函数将预测过程封装起来，以便于处理PyTorch Tensors
def predict_gnb(x):x = x.numpy()  # 将Tensor转化为numpy数组return gnb.predict(x)# 创建一个PyTorch Tensor作为测试数据
X_test_torch = torch.tensor([[9, 10], [11, 12]])# 使用封装好的predict函数进行预测
predictions = predict_gnb(X_test_torch)
print(predictions)

请注意，上述代码并没有直接在PyTorch中实现GaussianNB，而是利用了sklearn的实现，并通过适配使得其能处理PyTorch的Tensors。如果你想在纯PyTorch环境中实现GaussianNB，你需要自己编写相关的概率密度估计、似然计算以及分类逻辑等代码，这通常比直接使用sklearn要复杂得多。

六、总结

GaussianNB，即高斯朴素贝叶斯模型，是一种基于概率论的高效分类算法，在机器学习领域应用广泛。该模型的核心在于其对特征独立性和高斯分布的假设，通过计算训练集中各类别的先验概率以及在给定类别下各特征的高斯分布参数（如均值和方差），从而实现对未知数据的预测。尽管模型结构简洁，但其在处理大规模数据集时表现出高效能，尤其适用于文本分类、情感分析及疾病诊断等场景。然而，由于其对输入数据独立性的严格要求，当面对非线性或强相关性数据时，GaussianNB模型的拟合效果可能会受限。尽管如此，因其算法理解与实现相对简单，GaussianNB仍不失为一种实用且有价值的机器学习工具。