
目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2018年,G Dhiman等人受到自然界中帝企鹅群体社会行为启发,提出了帝企鹅优化算法(Emperor Penguin Optimizer, EPO)。
2.算法原理
2.1算法思想
EPO模拟了帝企鹅在寒冷冬季的聚集行为,群体通过产生热量来维持温暖。每个帝企鹅个体都会朝着群体中温度较高的方向移动,并寻找到达温度最高处的最优位置。在移动过程中,每个帝企鹅个体会根据自身与最优位置的距离进行调整,并不断更新最优位置,以此实现群体内个体的优化移动和位置更新。

2.2算法过程
计算拥挤周围温度分布:
群体中的温度T1的变化:
T 1 = T − M a x i t e r a t i o n k − M a x i t e r a t i o n , T = { 0 , if R > 1 , 1 , if R < 1. (1) \begin{aligned} &T_{1}=T-\frac{Max_{iteration}}{k-Max_{iteration}}, \\ &\left.T=\left\{\begin{array}{ll}0,&\text{if }R>1,\\1,&\text{if }R<1.\end{array}\right.\right. \end{aligned}\tag{1} T1=T−k−MaxiterationMaxiteration,T={0,1,if R>1,if R<1.(1)
其中,k为当前迭代次数,R表述个体距离拥挤群体中心的半径。
计算距离:
确定种群适宜的温度范围后 , 计算种群中每个个体与最优个体之间的距离:
D e p → = A b s ( S ( A → ) ⋅ P ( k ) → − C → ⋅ P e p ( k ) → ) . (2) \overrightarrow{D_{ep}}=Abs(S(\overrightarrow{A})\cdot\overrightarrow{P(k)}-\overrightarrow{C}\cdot\overrightarrow{P_{ep}(k)}).\tag{2} Dep=Abs(S(A)⋅P(k)−C⋅Pep(k)).(2)
其中,P,Pep分别表述最优个体位置和个体当前位置。A,C是避免相邻个体间碰撞的向量参数,S表示帝企鹅群体最优个体方向移动趋势。
S ( A → ) = ( f ⋅ e − k l − e − k ) 2 A → = ( M × ( T 1 + P g r i d ( A c c u r a c y ) × R a n d ) − T 1 P g r i d ( A c c u r a c y ) = A b s ( P → − P e p → ) . (3) \begin{aligned} &S(\overrightarrow{A})=\left(\sqrt{f\cdot\mathrm{e}^{-\frac{k}{l}}-\mathrm{e}^{-k}}\right)^{2}\\ &\overrightarrow{A}=(M\times(T_{1}+P_{grid}(Accuracy)\times Rand)-T_{1} \\ &P_{grid}(Accuracy)=Abs(\overrightarrow{P}-\overrightarrow{P_{ep}}). \end{aligned}\tag{3} S(A)=(f⋅e−lk−e−k)2A=(M×(T1+Pgrid(Accuracy)×Rand)−T1Pgrid(Accuracy)=Abs(P−Pep).(3)
位置移动:
P e p → ( k + 1 ) = P ( k ) → − A → ⋅ D e p → . (4) \overrightarrow{P_{ep}}(k+1)=\overrightarrow{P(k)}-\overrightarrow{A}\cdot\overrightarrow{D_{ep}}.\tag{4} Pep(k+1)=P(k)−A⋅Dep.(4)
伪代码:

3.结果展示
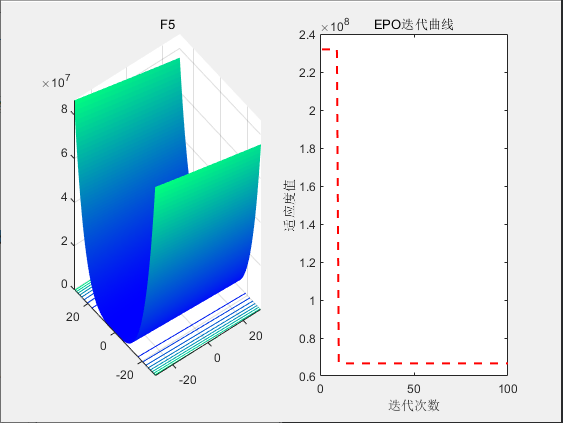
4.参考文献
[1] Dhiman G, Kumar V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems[J]. Knowledge-Based Systems, 2018, 159: 20-50.





基础算法)


)
)
)
:拷贝构造函数)


 -- for循环)


)

