超分辨率(4)--基于A2N实现图像超分辨率重建

一.项目介绍

已有研究表明，注意力机制对高性能超分辨率模型非常重要。然而，很少有工作真正讨论“为什么注意力会起作用，它又是如何起作用的”。

文章中尝试量化并可视化静态注意力机制并表明：并非所有注意力模块均有益。提出了Attention in Attention Block（A2N）用于高精确图像超分。具体来说，A2N由非注意力分支与耦合注意力分支构成。我们提出了Attention Dropout Module（ADM）为两个分支生成动态注意力权值，它可以用于抑制不重要的注意力调整。这使得注意力模块可以更专注于有益样例而无需其他惩罚，因此能够以少量的额外参数提升注意力模型的容量。

实验结果表明：所提方案可以取得比其他轻量化方法更好的性能均衡。Local Attribution Maps(LAM)实验同样表明：所提Attention in Attention A2结构可以从更宽的范围内提取特征。

文章主要贡献包含以下几点：

我们对神经网络不同阶段的注意力层有效性进行了量化分析，提出了一种有效的注意力层简直策略；
我们提出了一种Attention in Attention Block A2B，它可以为起内部分支动态生成和为1的注意力。由于其中一个分支为注意力分支，故而称所提模块为A2B；
基于A2B提出了A2N，相比类似网络的基线网络，所提方法可以取得更优异的性能。

论文地址：

[2104.09497] Attention in Attention Network for Image Super-Resolution (arxiv.org)https://arxiv.org/abs/2104.09497

源码地址：

haoyuc/A2N: PyTorch code for our paper "Attention in Attention Network for Image Super-Resolution" (github.com)https://github.com/haoyuc/A2N参考文章：

Attention in Attention for Image Super-Resolution - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/367501948

二.项目流程详解

2.1.Motivation

给定输入特征图 $\boldsymbol{F} \epsilon R^{C\textup{x}H\textup{x}W}$ （其中C、H、W分别是输入特征图的通道数、高度和宽度），注意力机制将预测一个注意力图 $\boldsymbol{M_{A}(F)} \epsilon R^{{C}'\textup{x}{H}'\textup{x}{W}'}$ （其中 ${C}'$ 、 ${H}'$ 、 ${W}'$ 的值取决于注意力机制的种类）。例如通道注意力机制会生成一个一维注意力图 $R^{C\textup{x}1\textup{x}1}$ ；空间注意力机制会生成一个二维注意力图 $R^{1\textup{x}H\textup{x}W}$ ；通道-空间注意力机制会生成一个三维注意力图 $R^{C\textup{x}H\textup{x}W}$ 。

至此文章作者提出两个问题：

what kind of features would attention mechanisms response to?
is it always beneficial to enhance these features?

即

图像的哪一部分具有更高或者更低的注意力系数呢？
是否注意力机制总是有益于超分模型呢？。

2.1.1.Attention Heatmap

LR空间中包含冗余的低频成分以及少量的高频成分。RCAN一文认为：无注意力的模型会对所有特征均等对待，而注意力有助于网络对高频特征赋予更多的注意。然而，很少有工作能够证实上述假设。

为回答上述所提第一个问题，我们通过实验来理解超分中注意力机制的行为。我们构建了一个包含10个注意力模块的网络，每个注意力模块采用通道和空域注意力层，因此每个像素具有独立的注意力系数。

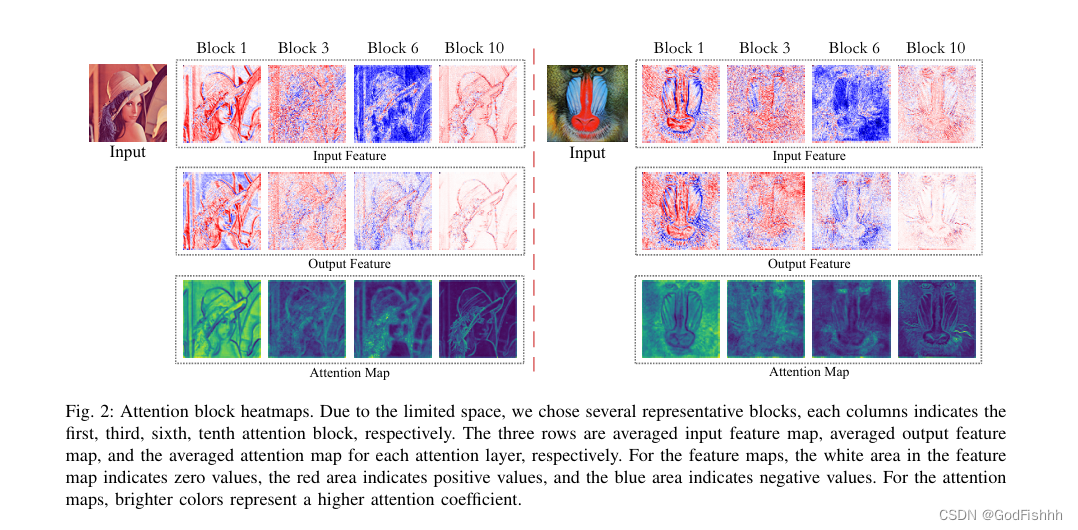
（上图为Heatmap。在特征图中，白色区域表示没有价值，红色区域表示有正面价值，蓝色区域表示有负面价值。在注意力图中，更加明亮的颜色代表着更高的注意力系数）

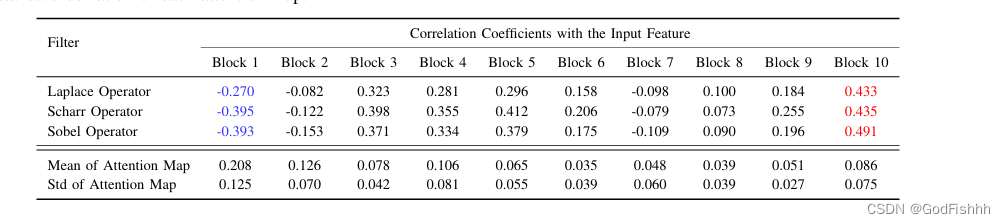
上图给出了某些特征与注意力图的可视化效果，上表给出了注意力图与高通滤波之间的相关系数。尽管这种度量方式无法精确度量注意力响应，但我们的目的是量化不同层之间的相对高通相关性。

从上图&上表可以看到：不同层学习到的注意力变化非常大。比如第一个注意力模块与第十个注意力模块表现处了截然相反的响应，意味着：低层的注意力模块倾向于低频模式，高层的注意力模块倾向于高频模块，中间的模块则具有混合响应。

2.1.2.Ablating Attention

基于上述的结果，我们尝试最大限度的减少注意力的使用，同时最小化额外参数量。一个最直观的想法就是只在关键性能层保留注意力层。但是，上述质量分析并不是一种有效的方法去量化注意力层的真实效果。

为定量度量注意力层的有效性，我们提出了Attention Dropout框架。我们通过关闭特定注意力层进行了一系列对比实验，结果见下表。

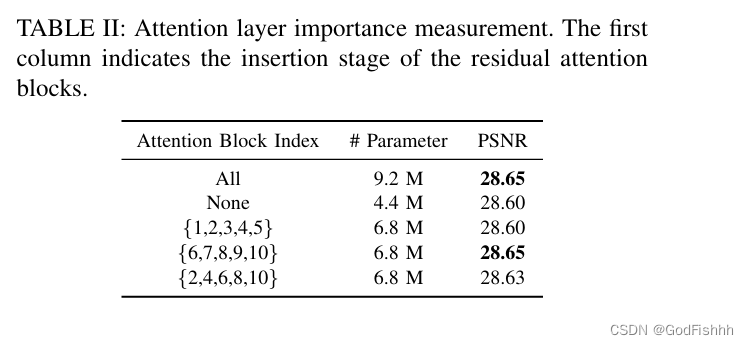
从上表可以看到：模块深度很大程度影响了注意力模块插入位置。该结果进一步验证了：全网络均匀的设置注意力是次优方案。

2.2.Method

2.2.1.Network Architecture

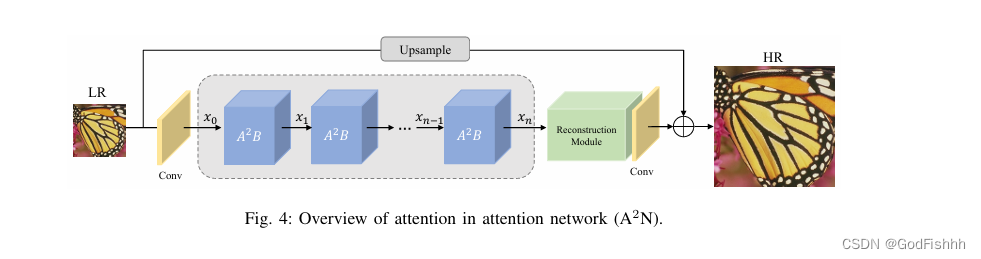
A2N架构由以下几个部分组成：

浅层特征提取：采用单个卷积层提取输入图像的浅层特征。

$x_{0} = f_{ext}(I_{LR})$

深层特征提取（堆叠A2B层）：采用链式堆叠A2B提取深层特征。

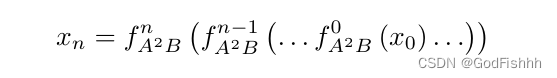
重建模块：完成深度特征提取后，我们通过重建模块进行上采样。在重建模块中，我们首先采用最近邻插值上采样，然后在两个卷积层中间插入一个简化版通道-空间注意力。

全局连接：最后采用全局连接，对输入的 $I_{LR}$ 通过最近邻插值上采样，然后与上述重建结果相加。

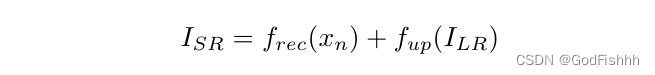
2.2.2.Attention in Attention Block（A2B）

受启发于动态核，文章提出了可学习DAM（Dynamic Attention Module）以自动丢弃某些不重要的注意力特征，平衡注意力分支于非注意力分支。具体来说，每个DAM采用加权方式控制注意力分支与非注意力分支的动态加权贡献。

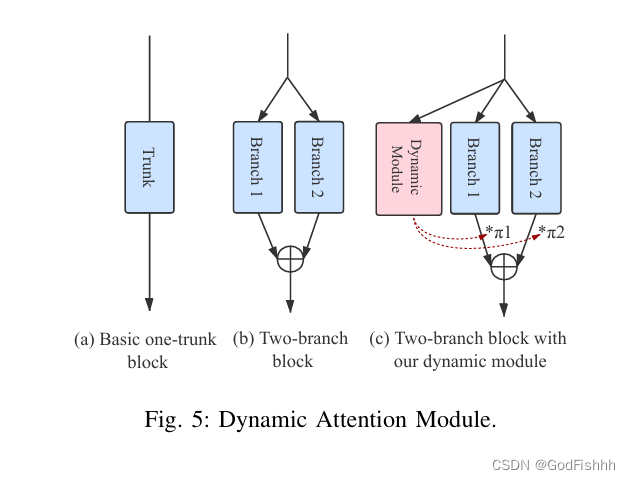
如上图所示，DAM根据输入为不同分支生成了动态加权权值，可以描述如下：

动态加权值的计算公式如下：

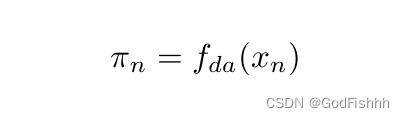
A2B结构如下图所示：

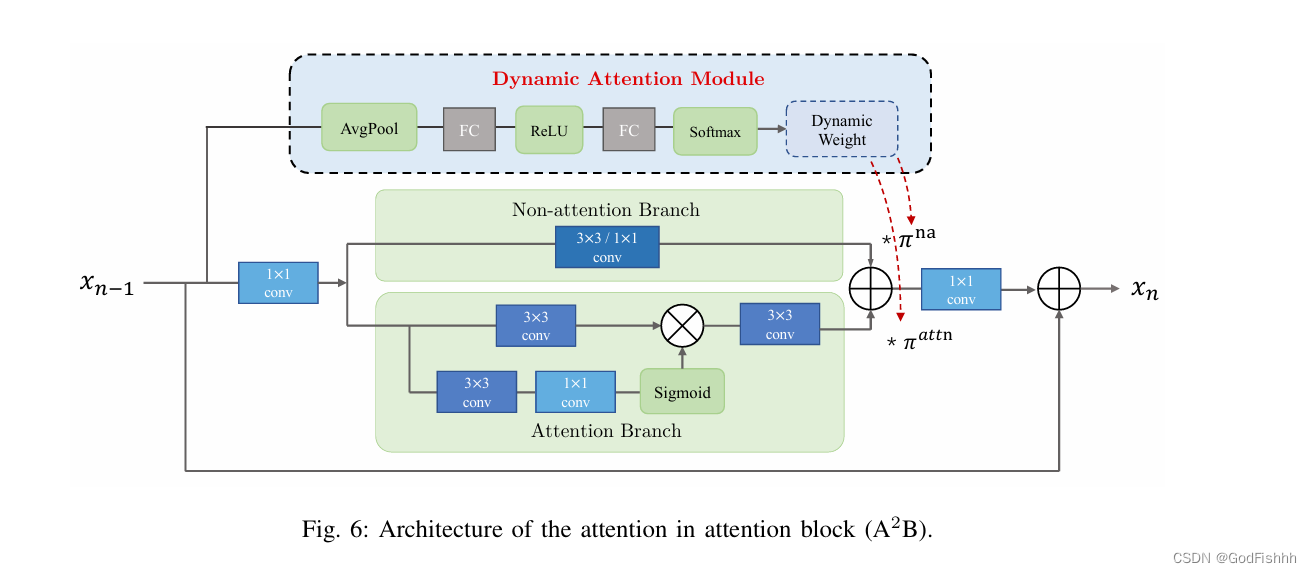
输入数据 $x_{n-1}$ 兵分三路进行处理：

$x_{n-1}$ 进入DAM，首先经过均值池化处理，再送入两个全连接层和Softmax层生成动态加权权值 $\pi ^{na}$ 和 $\pi ^{attn}$ （约束动态权值可以促进ADM的学习。文章中采用了sum-to-one来进行约束，即 $\pi ^{na}$ + $\pi ^{attn}$ = 1，这种约束方式可以压缩核空间，极大的简化 $\pi ^{na}$ 和 $\pi ^{attn}$ 的学习。）。
$x_{n-1}$ 进入中间模块，首先经过一个1x1的卷积层，而后再次分为上下两条线路，输入值在两条线路上分别经过一系列操作并与动态加权权值 $\pi ^{na}$ 和 $\pi ^{attn}$ 相乘后再相加，得到的结果最后进入一个1x1的卷积层。
$x_{n-1}$ 进入下面模块，在最终阶段与中间模块得到的 $\widetilde{x}^{n}$ 值相加得到最终的输出值 $x^{n}$ 。

代码实现：

import torch.nn as nn
import torch.nn.functional as Fclass AAB(nn.Module):def __init__(self, nf, reduction=4, K=2, t=30):super(AAB, self).__init__()self.t = t# K表示attention dropout module模块需要输出K个值，这里为2，并且相加为1self.K = K# 进出口的两个卷积层self.conv_first = nn.Conv2d(nf, nf, kernel_size=1, bias=False)self.conv_last = nn.Conv2d(nf, nf, kernel_size=1, bias=False)self.lrelu = nn.LeakyReLU(negative_slope=0.2, inplace=True)# 全局平均池化，输出为nf个值，这里nf为40self.avg_pool = nn.AdaptiveAvgPool2d(1)# Attention Dropout Moduleself.ADM = nn.Sequential(nn.Linear(nf, nf // reduction, bias=False),nn.ReLU(inplace=True),nn.Linear(nf // reduction, self.K, bias=False),)# attention branch 由 attention1和attention2组成self.attention1 = nn.Sequential(nn.Conv2d(nf, nf, kernel_size=3, padding=(3 - 1) // 2, bias=False))self.attention2 = nn.Sequential(nn.Conv2d(nf, nf, kernel_size=3, padding=(3 - 1) // 2, bias=False),nn.Conv2d(nf, nf, kernel_size=1, padding=(1 - 1) // 2, bias=False),)self.conv_attention = nn.Conv2d(nf, nf, kernel_size=3, padding=(3 - 1) // 2, bias=False)# non-attention branch# 3x3 conv for A2Nself.non_attention = nn.Conv2d(nf, nf, kernel_size=3, padding=(3 - 1) // 2, bias=False)# 1x1 conv for A2N-M# self.non_attention = nn.Conv2d(nf, nf, kernel_size=1, bias=False)def forward(self, x):residual = x# 分别获得输入数据的四个维度a, b, c, d = x.shapex = self.conv_first(x)x = self.lrelu(x)# Attention Dropout -- 最上层y = self.avg_pool(x).view(a, b)y = self.ADM(y)# ax用于保存得到的两个动态加权权值，所以ax应该是个[1,2]的数组ax = F.softmax(y / self.t, dim=1)# 中间层# attention部分# 先分别计算出上下部分得到的值attention1 = self.attention1(x)attention2 = self.attention2(x)attention2 = F.sigmoid(attention2)# 相加得到组合值attention3 = attention1 + attention2# 最后经过一个卷积层得到最终值attention = self.conv_attention(attention3)# non_attention部分non_attention = self.non_attention(x)# 分别乘以动态加权权值x = attention * ax[:, 0].view(a, 1, 1, 1) + non_attention * ax[:, 1].view(a, 1, 1, 1)x = self.lrelu(x)out = self.conv_last(x)# 最初值和中间值相加得到最后值out += residualreturn out