一、基本思想
MDS(Multidimensional Scaling ,MDS多维尺度变换)是一种经典的降维算法,其基本思想是通过保持数据点之间的距离关系,将高维数据映射到低维空间中。
具体来说,MDS算法的基本步骤如下:
1、构建距离矩阵:首先,我们需要计算原始空间中数据点之间的距离。常用的距离度量方法包括欧几里得距离、Minkowski距离等。通过计算每对数据点之间的距离,我们可以构建一个距离矩阵。
2、中心化距离矩阵:为了进一步处理距离矩阵,我们需要对其进行中心化处理,使得数据点相对于原点对称。
3、计算内积矩阵:通过中心化距离矩阵,我们可以计算内积矩阵B。内积矩阵表示数据点之间的内积关系,可以用于进一步分析数据的结构。
4、计算特征值和特征向量:在得到内积矩阵B后,我们需要计算其特征值和特征向量。特征值表示数据的主要变化方向,特征向量表示对应方向上的大小。我们将选取最大的k个特征值及其对应的特征向量,作为降维后的k维空间的基。
5、计算降维后的坐标:将原始数据投影到选定的k维基上,我们可以得到降维后的坐标。
通过上述介绍,可以知道,MDS可以将原始数据维度下降到任意维度。
二、MDS算法示例
让我们用一个关于水果口味的例子来说明MDS算法的原理。
假设有5种水果:苹果(A)、香蕉(B)、橙子(C)、葡萄(D)和菠萝(E)。我们对这些水果进行了甜度(Sweetness)、酸度(Sourness)和多汁程度(Juiciness)的评分。评分数据如下:
A:(6,4,5)
B:(8,1,3)
C:(5,7,6)
D:(7,3,4)
E:(4,6,8)
我们希望通过MDS算法将这些三维评分数据降维到二维空间,以便更直观地分析水果之间的口味关系。
步骤1:计算距离
我们可以使用欧氏距离(也可以用其他距离计算方法)来计算水果之间的距离。计算结果如下:
A-B: 4.69
A-C: 3.74
A-D: 2.45
A-E: 3.32
B-C: 6.56
B-D: 3.32
B-E: 6.56
C-D: 5.29
C-E: 2.45
D-E: 5.29步骤2:构建距离矩阵
将计算出的距离整合成一个距离矩阵D:
A B C D E
A 0.00 4.69 3.74 2.45 3.32B 4.69 0.00 6.56 3.32 6.56C 3.74 6.56 0.00 5.29 2.45D 2.45 3.32 5.29 0.00 5.29E 3.32 6.56 2.45 5.29 0.00步骤3:中心化距离矩阵
我们需要计算中心化矩阵H。数据点的数量n为5。因此,我们可以得到:
I=[1 0 0 0 00 1 0 0 00 0 1 0 00 0 0 1 00 0 0 0 1]
L=[11111]H=I-(1/5)*L*L^T
=[0.8 -0.2 -0.2 -0.2 -0.2-0.2 0.8 -0.2 -0.2 -0.2-0.2 -0.2 0.8 -0.2 -0.2-0.2 -0.2 -0.2 0.8 -0.2-0.2 -0.2 -0.2 -0.2 0.8]步骤4:计算内积矩阵
接下来,我们需要计算内积矩阵B。首先,我们需要计算距离矩阵D的平方:
D.^2=[0.00 21.98 13.99 6.00 11.0221.98 0.00 43.03 11.02 43.0313.99 43.03 0.00 28.00 6.006.00 11.02 28.00 0.00 28.0011.02 43.03 6.00 28.00 0.00]然后,我们用中心化矩阵H和距离矩阵D的平方计算内积矩阵B:
B=-0.5*H*D.^2*H=[2.12 -2.27 -1.07 1.12 0.11-2.27 15.33 -8.99 5.21 -9.29-1.07 -8.99 9.72 -6.07 6.421.12 5.21 -6.07 6.12 -6.370.11 -9.29 6.42 -6.37 9.13]步骤5:计算特征值和特征向量
我们需要计算内积矩阵B的特征值和特征向量。我们得到了如下特征值和特征向量:
特征值:lamda1=32.32 lamda2=6.39
特征值lamda1对应的特征向量V1=[-0.02 0.63 -0.48 0.36 -0.49]
特征值lamda2对应的特征向量V2=[-0.53 0.59 0.33 -0.50 0.10]我们选取最大的两个特征值λ1和λ2,以及对应的特征向量v1和v2,作为降维后的二维空间的基。
步骤6:计算降维后坐标
我们将原始数据投影到选定的二维基上,计算新坐标。首先,构建特征向量矩阵V和特征值矩阵Λ的平方根:
V=[-0.02 -0.530.63 0.59-0.48 0.330.36 -0.50-0.49 0.10]
对角矩阵A^0.5=[sqrt(32.32) 00 sqrt(6.39)]然后,我们计算降维后的坐标:新坐标 = A * A^(1/2)
新坐标=[-0.11 -1.333.60 1.50-2.76 0.842.02 -1.26-2.76 0.25]最后,我们得到了降维后的二维坐标:
苹果(A):(-0.11, -1.33 )
香蕉(B):(3.60, 1.50)
橙子(C):(-2.76, 0.84 )
葡萄(D):(2.02, -1.26 )
菠萝(E):(0.36, 2.89)三、基于MATLAB的MDS示例代码
MATLAB中自带降维函数cmdscale,实现代码如下:
clc;
clear;
data=[0.0,4.69,3.74,2.45,3.32;4.69,0.0,6.56,3.32,6.56;3.74,6.56,0.0,5.29,2.45;2.45,3.32,5.29,0.0,5.29;3.32,6.56,2.45,5.29,0.0];
Y=cmdscale(data);如果将数据降维为2维,则取前2列,结果如下:
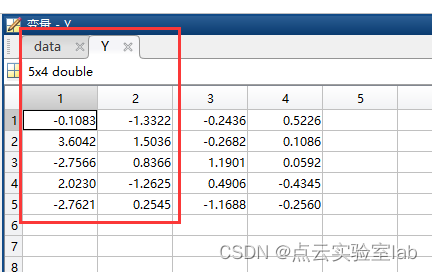
如果按照上述原理,编写程序,代码如下:
D=[0.0,4.69,3.74,2.45,3.32;4.69,0.0,6.56,3.32,6.56;3.74,6.56,0.0,5.29,2.45;2.45,3.32,5.29,0.0,5.29;3.32,6.56,2.45,5.29,0.0];I=[1,0,0,0,0;0,1,0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1];
L=[1;1;1;1;1];
L*L';
H=I-(0.2)*L*L';
D2=D.^2;
B=-0.5*H*D.^2*H;
[v,d]=eig(B);
lamda1=d(1,1);
lamda2=d(2,2);
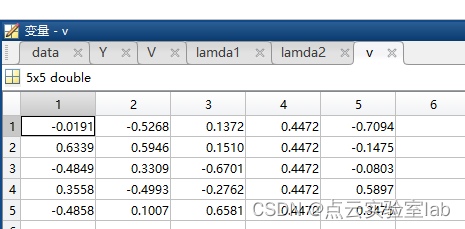
duijiaojuzhen=[sqrt(lamda1),0;0,sqrt(lamda2)];
V=[v(:,1),v(:,2)];
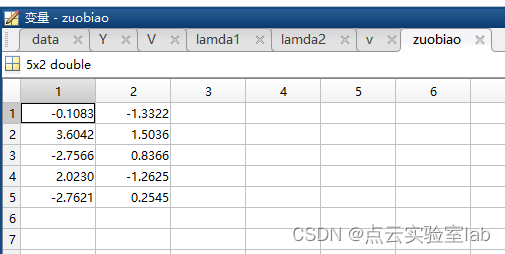
zuobiao=V*duijiaojuzhen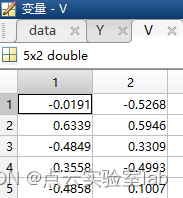
四、总结
下面是一个关于MDS算法优缺点的表格:
| MDS的优点 | MDS的缺点 |
|---|---|
| 计算相对比较容易而且不需要提供先验知识。 | 当数据量较大时,运算时间可能较长。 |
| 在降维过程中尽量保持数据点之间的距离关系,有助于挖掘数据中的结构信息,适用于各种类型的数据,如距离、相似性、关联性等。 | 各个维度的地位相同,无法区分不同维度的重要性。 |
参考博客:【数据降维-第4篇】多维尺度变换(MDS)快速理解,及MATLAB实现 - 知乎

—— 我的藏书馆)









)


)

--实现堆内存管理)


