首先 Oh My Zsh 是什么?
- Oh My Zsh 是一款社区驱动的命令行工具,正如它的主页上说的,Oh My Zsh 是一种生活方式。它基于 zsh 命令行,提供了主题配置,插件机制,已经内置的便捷操作。给我们一种全新的方式使用命令行。
- Oh My Zsh 是基于 zsh 命令行的一个扩展工具集,提供了丰富的扩展功能。
安装 Oh My Zsh 方法:
- 安装方式是有很多种,常见的方式是通过 curl 或 wget 两种方式来安装,具体操作可以参考:Installing ZSH · ohmyzsh/ohmyzsh Wiki · GitHub
Oh My Zsh安装完成后,需要安装 zsh-autosuggestions 插件:
1.使用git克隆zsh-autosuggestions仓库到你的本地.oh-my-zsh/custom/plugins目录:
git clone https://github.com/zsh-users/zsh-autosuggestions ~/.oh-my-zsh/custom/plugins/zsh-autosuggestions 2.然后使用 vim ~/.zshrc,找到下面的脚本位置,添加zsh-autosuggestions: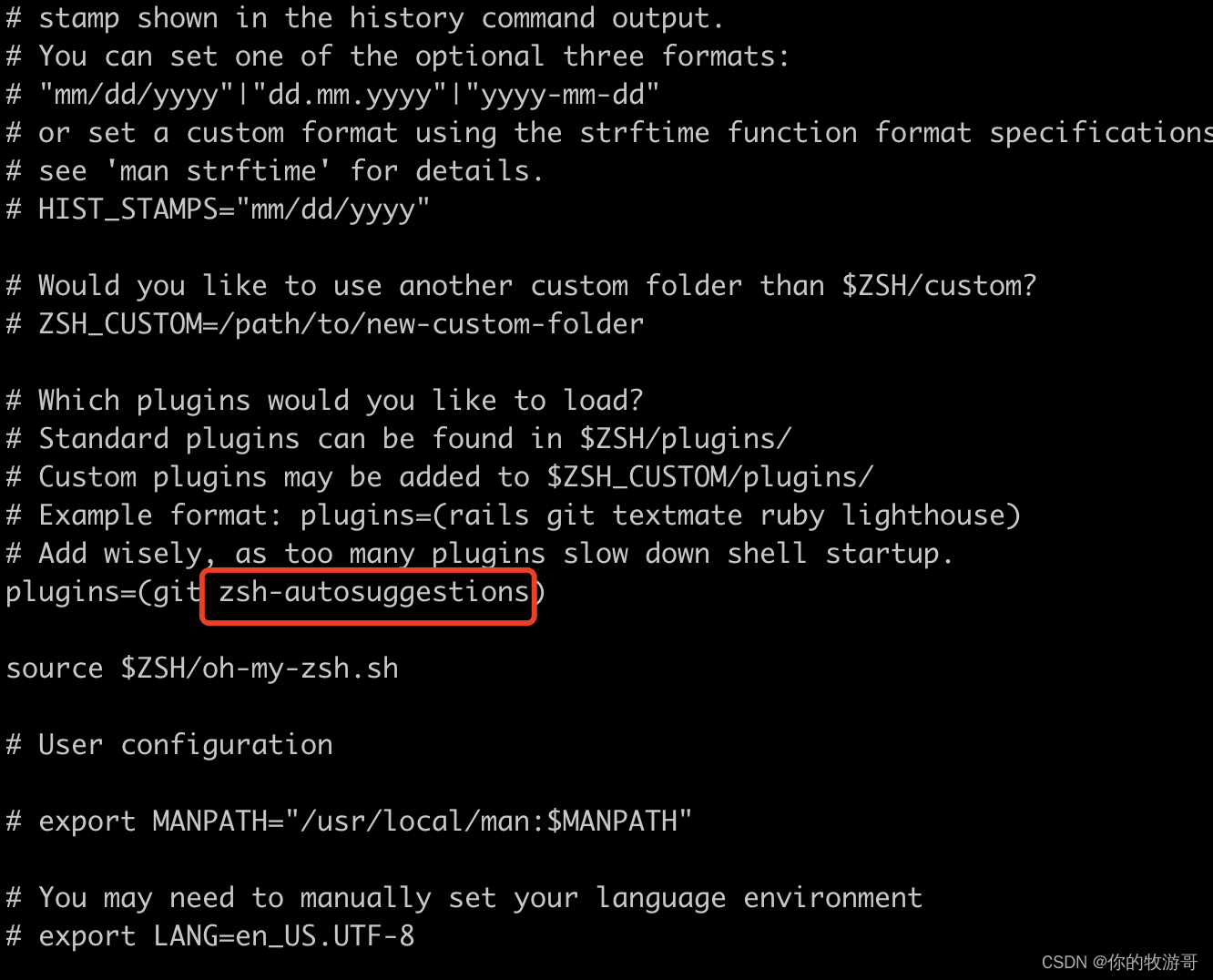
3.保存并关闭.zshrc文件,然后执行以下命令来使插件生效:
source ~/.zshrc4.查看效果,我们在输入git命令时,就能实现命令自动补全的功能了



>)







原理及实现)







——(8))
