题目要求：

给你一个整数 n 。现有一个包含 n 个顶点的 无向 图，顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。

返回图中 完全连通分量 的数量。

如果在子图中任意两个顶点之间都存在路径，并且子图中没有任何一个顶点与子图外部的顶点共享边，则称其为 连通分量 。

如果连通分量中每对节点之间都存在一条边，则称其为 完全连通分量 。

示例 1：

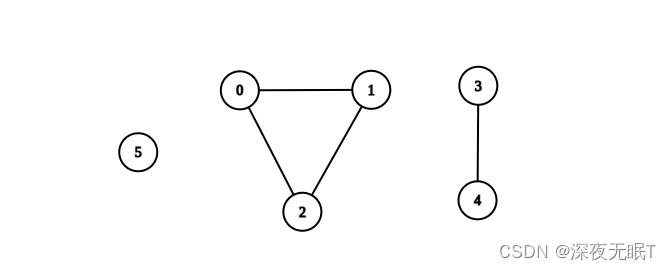
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出：3
解释：如上图所示，可以看到此图所有分量都是完全连通分量。

题目解析：

题目中要求输入一个整数和一个数组，整数代表一共有几个顶点，二维数组表示这几个顶点之间有没有连线。最后要求输出这个顶点中完全连通分量的个数，所谓的完全连通分量是指几个顶点之间相互连接，没有任何一个顶点与子图外部的顶点共享边。也就是要围成一个圈。

当读完题第一时间想到的方法就是使用并查集的方式找出分量的数量，再去判断该分量是不是完全连通分量。

并查集的方法再此就不多做解释了，具体可见我的另一篇博客，里面我具体介绍了并查集算法的思想以及实现。

LeetCode547——省份数量（并查集）

当实现完并查集后，我们就可以得到连通分量的个数，之后我们就要去判断该连通分量是不是完全连通分量了。

这里需要用到一些数学的思维，我们可以通过整个图中边和点的数量来判断该图是不是完全连通分量，如果图中有m个顶点，有n条边，当n=m*(m-1)/2时。因为每个节点都要与其他的节点具有边，因此要m*(m-1),但是这样会重复统计，因此还要除以2.所以当边和顶点数满足此关系时，其就是个完全连通分量。就像当有四个顶点时，应有下图：

所以下面我们就要拿到每个连通分量中的顶点数和边数。这里我用了两个哈希表来表示。

用哈希表的key表示连通图的序号，用value表示拥有的点和边。

首先遍历p数组，数组中表示每个顶点的父节点，一个父节点就可以表示一个连通图，因为一个连通图的父节点都是一样的，如果其父节点存在，那么把该点加到该连通分量中，否则再哈希表中新加入一个key值。

但是由于本题中一个节点可能会连接3个乃至更多的节点，并且连接结构可能比较复杂，所以最后得到的数组中可能并不完善，可能会有间接的父节点，就比如我们可能会得到数组{1，2，2，2},这个是存在间接父节点的，第0个节点的父节点是1，第一个元素的父节点就2.这个数组就等价于{2，2，2，2}。

因此我们不能直接用p[i]来找到其真正的父节点，要再次使用一次find方法才能找到其真正的父节点。

在寻找边时我们就可以直接遍历输入的二维数组，将边的数量放入到哈希表中。

最后我们再次遍历节点，找到每个节点的父节点，根据哈希表得到边和顶点的数量进行判断，当一个父节点判断过后就将设设为-1，在循环中遇到-1直接跳到下一次循环，因为等于-1时该连通分量已经计算过了。遍历结束后我们就得到了答案。

代码实现：

class Solution {public int countCompleteComponents(int n, int[][] edges) {int len = edges.length;int[] p = new int[n];for(int i=0;i<n;i++){p[i]=i;}for(int j=0;j<len;j++){union(p,edges[j][0],edges[j][1]);}Map<Integer,Integer> map = new HashMap<>();for(int k =0;k<n;k++){int f = find(p,k);if(!map.containsKey(f)){map.put(f,1);}else{map.put(f,map.get(f)+1);}}Map<Integer,Integer> s = new HashMap<>();for(int i=0;i<n;i++){s.put(i,0);}for(int i=0;i<len;i++){int key = find(p,edges[i][0]);s.put(key,s.get(key)+1);}int res=0;for(int i=0;i<n;i++){int x = map.get(p[i]);if(x==-1){continue;}if(s.get(p[i])==(x*(x-1))/2) res++;map.put(p[i],-1);}return res;}public void union(int[] p,int index1,int index2){p[find(p,index1)]=find(p,index2);}public int find(int[] p,int index){if(p[index]!=index){p[index]=find(p,p[index]);}return p[index];}
}