highlight

我们建立了一个带有冷却器和冰热能储存的建筑能源系统模型。

提出了一种两阶段鲁棒策略来调度系统运行。

具有适当参数的鲁棒策略优于确定性方法。

鲁棒策略和MPC方法的性能相似。

 本文提出了一种鲁棒调度策略，用于在预测不确定的情况下管理具有太阳能发电系统、多机组和冰蓄能的建筑能源系统。该策略采用两阶段可调鲁棒公式来最小化系统运行成本，其中引入参数来调整鲁棒解相对于建模不确定性的保守性水平。然后，采用一种具有修改初始化策略的列和约束生成算法，与混合整数线性规划一起求解该优化模型。此外，我们通过蒙特卡洛模拟每小时模拟一个实际项目的系统运行来评估所提出的策略的性能。数值结果表明，在所有研究情况下，具有适当参数的鲁棒调度都优于确定性策略。此外，所提出的策略与基于模型的预测控制策略具有相似的结果，而前者只需要实现一次。即使在最高负载的情况下，两种策略之间的相对偏差也小于2%

蒙特卡洛模拟作为一种常用的模拟技术，在PMBOK里经常可以看到它的身影，其主要出现在风险管理知识领域中的定量风险分析过程，是用于做项目定量风险分析的工具之一，同时蒙特卡洛模拟也可以用于估算进度或成本以及制定进度计划等。

蒙特卡洛模拟是在计算机上模拟项目实施了成千上万次，每次输入都随机选择输入值。由于每个输入很多时候本身就是一个估计区间，因此计算机模型会随机选取每个输入的该区间内的任意值，通过大量成千上万甚至百万次的模拟次数，最终得出一个累计概率分布图，这个就是蒙特卡洛模拟。

作者：项目管理漫笔
链接：https://www.zhihu.com/question/263316961/answer/362674489
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

综合能源系统(IES)为新建筑或现有建筑提供了一种有前途的方法，这是世界上的主要能源消费者之一[1]。IES是一个复杂的系统，其目标是同时提供电、空间冷却、空间加热载荷和其他载荷，如热水和蒸汽[2,3]。在这样的系统中，电能可以来自太阳能、风能和组合热和电力系统等分布式能源资源，而冷却能量可以通过使用废热或地源热泵利用地热能吸附冷水机组提供。购买或产生的能量也可以存储在电或热能存储系统中，然后发布以满足其他时间的需求。为了充分挖掘IES的潜力和优势，制定有效的运营策略至关重要。请注意，能量存储将调度问题耦合到多个时间段，这增加了系统操作的复杂性。在本文中，我们重点开发了一种集成太阳能发电系统（SPGS）、多机组系统和冰蓄能系统（ITES）的建筑IES的优化运行方法。 

对于建筑能源系统来说，在炎热天气下，空间冷却占能源消耗的很大一部分[4]。为了降低能耗成本，特别是冷却成本，在多机组系统和热能储存的应用和优化控制方面做了大量工作[5-8]。由于其灵活的操作，多机组系统可以满足不同的负荷需求，并且在动态电价下，热能储存有可能将电力负荷从高峰时段转移到非高峰时段[9]。Fan等人[5]将冷负荷比的概率密度分布剖面划分为几个范围，并进一步根据不同的负载需求分别优化了冷却器的运行。结果表明，与原来的顺序控制策略相比，这种策略可以节省更多的功耗。在[6]中，Ma等人提出了一种用于中央冷水机组的在线自适应最优控制策略，并获得了类似的结果。对于具有热能储存的能源系统，Wang等人[7]应用储存优先策略来协调冷却器和储存。然而，这种确定性的方法不能充分利用热能存储器来降低运行成本。

为了使系统及时响应冷负荷的变化并充分利用热能储存，许多研究人员将基于模型的预测控制（MPC）方法应用于建筑能源系统[10-17]和微电网[14，18]的运行。由于实际操作和滚动机制的反馈，MPC可以在预测期内适当调整操作调度。由于实际操作和滚动机制的反馈，MPC可以在预测范围内正确调整操作调度。Zhao等人[13]使用MPC策略优化具有热能存储的建筑调度，并达到所需的性能。除了[13]中所研究的能源系统的非线性特性外，Lu等人[9]提出了一种基于MINLP的最优调度策略，考虑了一些设备的开/关数量等离散特征，比NLP方法更具竞争力。在[16]中，作者开发了一种混合整数非线性规划模型，通过MPC策略模拟具有热能存储的中央冷水机组的运行，并提出了一种启发式算法来解决这一问题。请注意，负载需求[19]和可再生能源[20]的预测不准确可能会影响MPC策略的性能。在预测不确定性方面，提出了自适应多MPC方法[21]、MIN-MAX MPC鲁棒最优控制方法[22]和随机规划[23]来处理不确定性。然而，[22]中获得的解可能是过度保守的;不确定变量的分布必须在[23]中提前知道，这使得在实践中很难实现。相比之下，[24]中给出的鲁棒模型不需要不确定变量的分布，并允许决策者自己调整解的保守性水平。出于这个原因，近年来该方法受到越来越多的关注[25-29]。Alessandra等人[26]提出了一种能量枢纽运行管理的鲁棒模型，并考虑了模型的不确定参数，获得了鲁棒解，但它们没有考虑负载的不确定性。[27,29]中的作者使用两阶段鲁棒优化方法来解决电力系统运行领域的单元承诺问题。在[28]中研究了考虑不确定需求的鲁棒位置运输问题。然而，现有文献的工作很少是通过具有可调保守性水平的稳健优化来调度不确定性下的建筑能源系统，特别是两阶段稳健优化。

上述研究要么用确定性方法调度建筑能源系统，要么滚动，用MPC方法运行冷水机组和热储能。虽然MPC方法有可能及时调整调度，但滚动优化仍然是确定性的，并且严重依赖于负载需求和可再生能源发电的预测[14]。上述一些策略能够使系统对不确定性更加健壮，但这些解决方案可能过于保守，这可能会提高操作成本以处理很少出现的最坏情况。本文针对具有太阳能发电系统、多机组系统和冰蓄能系统的建筑能源系统，建立了两阶段鲁棒优化模型，研究了不确定的冷负荷、电力负荷和太阳能对系统运行的影响。两阶段鲁棒性方法打算考虑两组变量。第一组是“当前”变量，如冷却器的开/关状态和冰热能系统的排放/充电模式，这些变量需要在不确定性揭示之前确定。相比之下，第二组是“观望”变量，例如冷却器的输出，这些变量可以在不确定性披露后确定[28]。采用列和约束生成算法[30]来求解所提出的具有修改初始化策略的两阶段鲁棒模型。所研究的建筑能源系统具有两级控制结构[16,17]：监督控制和局部控制。监督控制层负责根据预测的太阳能和负载需求，在展望期内优化系统运行。本地控制层根据来自监控层的操作调度来管理设备。本文主要研究建筑能源系统的监督控制。

2. System modeling

所研究的建筑能源系统位于中国天津国家电网公司客户服务中心北基地，如图1所示。该基地是一个呼叫中心和供电技术研发中心，共有10栋建筑（总净建筑面积113485平方米），包括5栋办公楼和5栋公寓楼。建筑有不同的能源需求，如电力负荷、夏季空间制冷、冬季空间供暖、热水。在这里，我们重点关注他们的电气和空间冷却需求。在该系统中，太阳能发电系统和公用电网向整个基地供电；中央制冷系统在夏季为建筑物降温，包括三台地源热泵（GSHP）、两台水冷式制冷机（WCC）和一个冰热能存储系统。ITES上游带冷却器，由两台冷却器和一个储冰罐组成。中央制冷机系统采用恒定的一次流量和冷冻水供应温度，这意味着在线制冷机和ITES将根据一些规则共享负载，如[5]中描述的相同部分负载比（PLR）。如前所述，我们研究了监控级别的系统操作。在下一节中，为了优化冷却器的承诺以及ITES的排放和充电计划，我们对建筑能源系统的每小时运行进行了建模，目的是在展望期内将能源成本降至最低。请注意，本文中的建筑模型是用每小时预测的总能源需求来描述的，而不是用建筑物的物理特性来描述的。

2.1. Ground source heat pumps and water-cooled chillers 地源热泵和水冷式冷水机组

地源热泵是利用地热能进行空间供暖和制冷的环保型热泵，这里考虑了制冷模式。由第i个热泵提供的每小时冷却量及其在小时t的能量消耗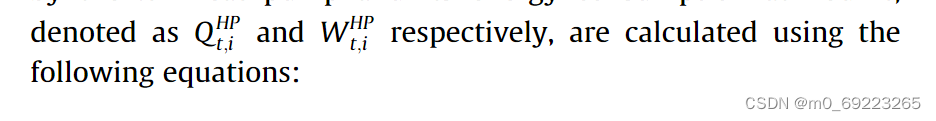

2.2. Ice thermal energy storage system 

冰热能储存系统包括冷却器、储冰库和辅助设备，如冷却水泵、冷冻水泵和热交换器。当使用时间（TOU）电价较低时，冷却器会向冰库充电。在高电价时期，ITES系统可以通过冷却器、储冰库或两者提供冷却负载。在该项目中，ITES系统循环乙二醇溶液以生产冰，并通过热交换器与返回的冷冻水传递热量，用于空间冷却。我们通过等式来区分ITES系统在t小时的冷却模式和制冰模式式（6）。

并且进一步通过等式（7）选择每个冷却器的操作模式。

等式（8）限制了乙二醇泵的运行数量。

等式（9）区分了储冰盒的充电和放电模式。

方程（10）给出了由蓄冰器、冷却器和ITES系统提供的冷却功率的关系。

如果ITES系统打算提供冷却负荷，则应根据与这些系统相关的相应冷冻水泵的额定流量，与热泵和水冷式冷却器分担负荷，如等式（11）所述。

我们引入等式（12）和（13）来计算每个冷却器和所有冷却器一起提供的冷却功率。

储冰盒的充电和放电行为由（15）和（16）描述。

在t时由冷却器提供的存储的冷却功率的量，其可以通过等式（17）和（18）来计算。

冷却器在其制冰模式下的部分负载比，其由等式（19）限制。

我们引入了方程。（20）-（23）来模拟ITES为冷却负载供电时冷冻水泵和乙二醇泵的开/关模式。等式（20）和（22）根据ITES系统提供的总冷却能量启动和停止泵，而（21）和（23）基于与冷却器的一对一匹配来确定泵的运行数量。

ITES系统在t处消耗的总能量，计算为等式（24），其中右手侧的第一项用于估计供应冷却负载和储冰库的冷却器消耗的功率，第二项是乙二醇泵在排放模式下消耗的功率和最后一项是冷冻水泵消耗的功率。在本文中，我们假设乙二醇泵消耗的功率与ITES系统提供的总冷却功率成比例。

2.3. Solar power generation system and utility grid

该项目安装的太阳能发电系统为个人使用，发电由政府补贴。如果电力负荷大于太阳能，系统将自动从公用电网购买电力，购买电力不应超过等式（25）中给出的联络线允许电力的最大值。

2.4. Power balance

建筑能源系统的需求和供应应满足以下平衡关系

为了便于在下面的小节中进行描述，我们引入以下公式。

2.5. Deterministic formulation

在本文中，我们打算在预测期内最小化系统运行成本，

如objective：等式所示（31），

s.t.   应受到等式（1）-（30）的约束。

注意，等式（1）、（3）、（11）、（12）和（18）的约束涉及二进制和连续变量的乘积项，因此它们是非线性的。这些项可以通过引入新的连续变量和一组线性不等式来线性化，方法是使用[32]中提出的技术。

此外，除了方程（11）和（15）之外，（1）-（30）中公式的等号可以用“>=”的符号代替，而不影响所考虑的优化问题的最优值。通过（15）中给出的递归关系，我们还可以将方程（15）和（16）组合成不等式。

为了简洁起见，我们给出了优化问题[27]的紧致矩阵公式：
上述公式为混合整数线性规划，其中x表示由（1）-（30）中所有设备的运行模式组成的所有二进制变量，y表示所有连续变量，包括用于空间冷却、负载需求、太阳能发电和从电网购买电力的设备的输出和功耗。约束（33）对应于等式（6）-（8）、（21）和（23）；约束（34）指的是方程（5）、（10）、（13）-（17）、（19）和（25）-（27）；约束（35）指示等式（11）；约束（36）表示等式（1）-（4）、（9）、（12）、（18）、（20）、（22）和（24）；

 3. Two-stage robust optimization model

在本节中，考虑了太阳能和负荷需求的不确定性，提出了建筑能源系统的两阶段鲁棒调度模型。其一般方法如图所示。下面的小节描述了详细的建模过程。

3.1. Robust formulation

当我们考虑前瞻期内的系统运行时，在披露不确定的需求和太阳能发电之前，需要首先确定每个冷却器的运行模式，如开/关状态。然后，当不确定性被揭示时，可以决定冷却器和储冰器的输出。所提出的两阶段鲁棒方法旨在获得第一阶段的操作模式的解决方案，该解决方案不受不准确预测导致的所有不确定场景的影响，而第二阶段负责根据第一阶段的最优解找出最坏情况下的调度成本。这里，我们将x视为第一阶段变量，将y视为第二阶段变量。自然地，与x相关的公式，即方程（33），被选择作为第一阶段约束

 与y相关的方程（34）-（37）被视为第二阶段方程。

注意，约束（36）耦合变量x和y，这意味着这些变量是相互依存的。这就是为什么我们需要两阶段分解技术来解决如下所示的相关问题。

        在本文中，我们考虑以下不确定性集，表示为U，来描述展望期内太阳能发电和负荷需求预测的不确定性，即：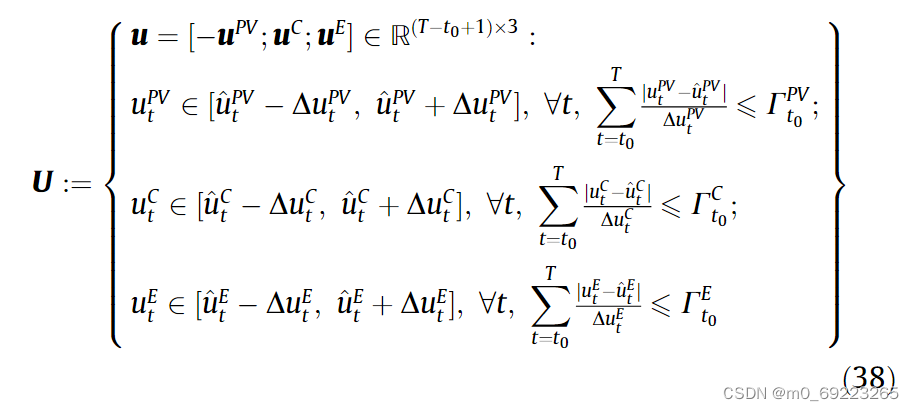 

        确定性公式的两阶段鲁棒对应物的详细表达式如下所示： 

        给出了每个固定x和u的第二阶段变量的可行解的集合。从上面的公式可以看出，两阶段鲁棒方法旨在获得第一阶段解，该第一阶段解对于所考虑的不确定性集的任何实现都是可行的，并且即使在最坏的情况下也具有最小的调度成本 。方程中描述的公式。（39）和（40）是一个三级最小-最大-最小混合整数规划，一些文献[27，29，30]研究了其求解算法。

          在本文中，我们应用列和约束生成方法（C&CG）[30]来求解优化模型。与Benders对偶算法类似，该方法迭代求解主问题和子问题。不同之处在于，C&CG通过迭代引入与子问题相关的新变量和约束来优化主问题。该方法有助于获得更严格的目标下界，从而减少迭代次数。与上述公式相关的主要问题表示如下：

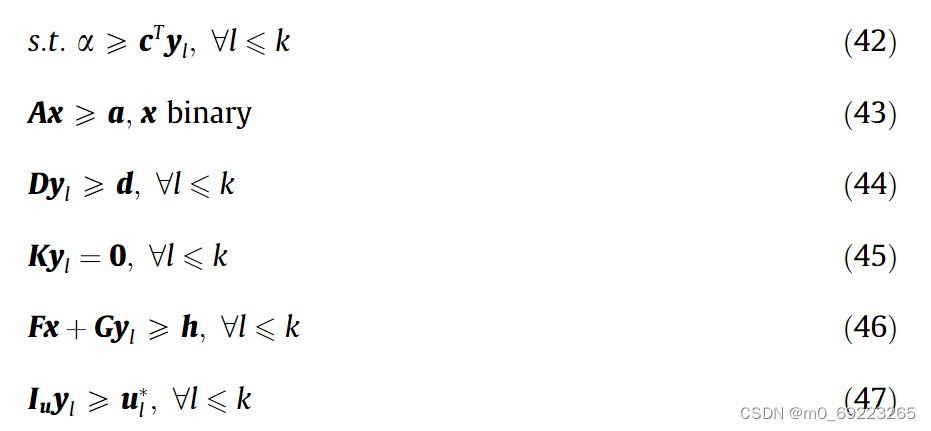
所考虑的子问题如下:

上式具有极大极小形式，其中对于固定的x和u，内极小问题是线性的。利用强对偶理论，子问题可以重刻成以下等价的极大形式，即: 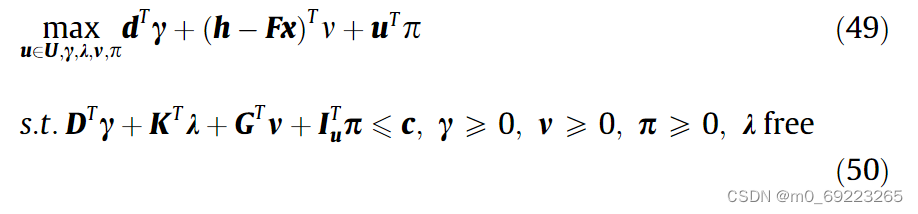经过以上变换，Eq.(49)中的utp项变成了二元变量与连续变量的乘积形式。进一步，利用上述线性化技术[32]，将子问题的最大形式重新塑造为以下混合整数线性优化模型，即:

3.2. Algorithm

The C&CG algorithm adopted is described as follows:

4. Numerical results

4.1. Robust scheduling

        在本节中，对所提出的方法在如图1所示的建筑能源系统上进行了测试。主要系统参数如表1所示。在实例研究中，提出了一种基于预测负荷和太阳能发电的鲁棒调度方案，并将该优化方案应用于考虑实际负荷和太阳能发电的系统实际运行仿真。我们使用MATLAB和GAMS来实现优化和仿真。C&CG算法的间隙容差设置为0.005。

        我们通过在给定范围内随机抽样来建立预测每小时负荷需求和太阳能发电的模型。首先以夏季设计日的冷负荷和电负荷为参考，模拟建筑的实际小时负荷需求，如图3所示。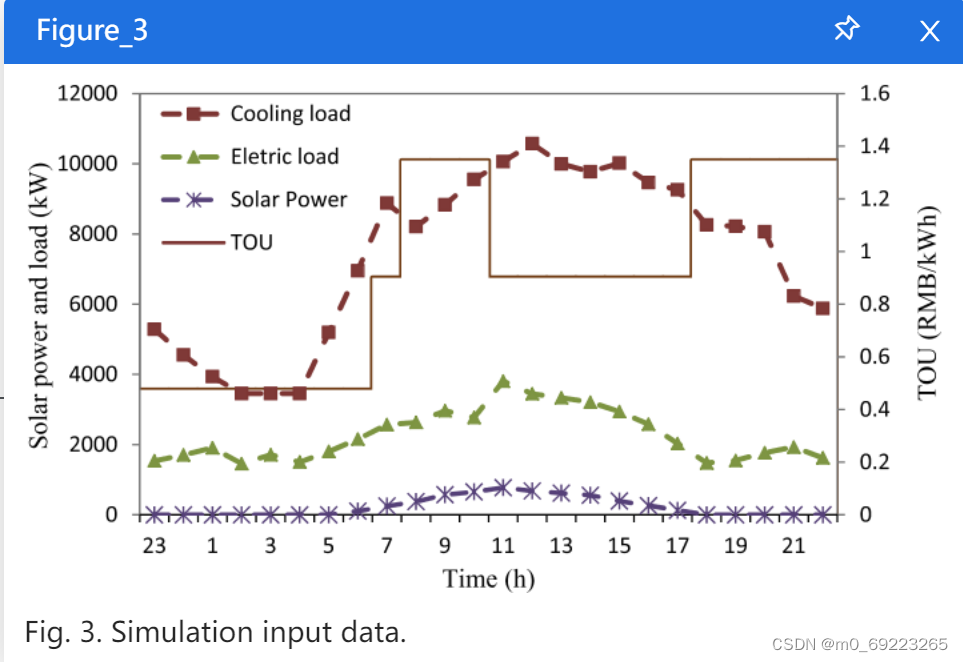        然后，将每小时独立的扰动添加到设计负载中，以生成预测负载的样本。假设扰动服从正态分布，均值为0，标准差(Std)为设计荷载的一定百分比[33]的三分之一。假设冷负荷的百分比在前10小时内从3%线性增加到10%，在剩余时间内取10%的值。对于电负载，除了6%到15%的百分比外，也做了类似的假设。对于太阳能，我们仅假设其加性扰动是独立且正态分布的，均值为0，标准差为给定的发电剖面在晴天中的恒定百分比的三分之一，如图3所示。相应的百分比设置为8%，发电概况也用于模拟未来期间的实际太阳能发电量。此外，图3描述了分时电价。

        一旦获得预测的太阳能功率和负荷，即^u，我们估计不确定性偏差，将预测乘以上述各自干扰百分比的“折扣”。在本文中，我们假设“折扣”可以取0.68/3, 1/3, 2/3或1，这意味着实际负荷和太阳能发电将以不同的概率落入预测区间。如何计算这些详细的概率值在附录A中给出。

在系统实际运行的模拟中，如果由于不确定性，计划运行的冷水机组和冰库不能满足实际冷负荷需求，则需要对即将到来的调度进行一些修改。调整原则如下:

(a)如调度不给冰库充水或放水，则启动之前未被调度运行的冷水机组;如果所有冷水机组仍不能满足当前负荷，则将冰库放空。

(b)如果计划对冰库收费，则在其他冷水机组不能满足负荷的情况下，该计划将被终止。

(c)若调度排冰，启动未运行的冷水机组。

(d)如果所有运行设备的总容量大于当前调度或后续修改后的实际负荷，尽可能关闭部分冷水机组。由于建筑能源系统与电力平衡的公用事业电网相连，因此无需对电力负荷进行任何修改。

考虑上述鲁棒调度和实际运行策略，建筑能源系统运行仿真结果如图4所示。

         与预测的冷却载荷相比，最坏情况发生在第 9 至 20 小时的载荷达到其上限，而其余的则满足预测值。在实际操作过程中，在这种情况下不会更新鲁棒调度。在前 8 小时，由于电价较低，初始容量为 0 的冰库被收取达到接近其最大容量的水平，并且当价格较高时，大部分是排放的。

        在其他时期，热泵和水冷式冷却器负责满足冷却负荷。注意，在给定情况下，冰热能存储系统中的冷却器不被安排为直接供应冷却负载。本案冷却成本为16535元，占包括购电和太阳能发电补贴在内的总运营成本（负成本）的27.86%。请注意，SPGS的峰值容量小于能源系统的最小电力负载，因此所有太阳能将用于供应电力负载。此外，该系统还与公用电网相连，从而自动平衡电力。换句话说，电力负荷和太阳能的预测误差不影响鲁棒解。因此，我们在以下分析中重点关注不同设计负荷比例的不确定冷负荷对系统运行成本的影响。

4.2. Tao_t0_C的敏感性分析

        预测冷负荷的“不确定性预算”可以取0到24之间的值。在这里，我们使用蒙特卡罗模拟方法来分析不同Tao_t0_C值对系统运行成本的影响。表2给出了针对不同的Tao_t0_C值、不同的冷却负荷需求和1/3的“折扣”，所提出的稳健调度方法的冷却运行成本的平均值和标准偏差。通过500次模拟计算出每个案例的统计结果。表2还给出了由具有收缩期的经济MPC策略控制的能源系统的运营成本[34]，其中该模型与第2.5小节中建立的确定性公式相同。MPC的预测每小时更新一次，原则与第4.1小节第二段所述相同。此外，表2的最后一行给出了滚动鲁棒调度（RRS）的解决方案，以与MPC的解决方案进行比较。与所提出的仅实现一次的鲁棒调度不同，RRS策略每小时将鲁棒方法应用于系统运行，类似于MPC方法。

        在设计冷负荷的25%、50%和75%的情况下，总有比相应的确定性优化结果具有更好平均值和标准偏差的解，即Tao_t0_C的情况。相反，当需求被视为设计冷却负载的100%时，鲁棒性解决方案变得更差。原因是鲁棒调度更有可能将具有高电价和冷却需求的时段视为最坏情况的潜在部分，这导致储冰盒通常将被安排在这样的时段期间排出。

        然而，在高负荷需求的情况下，计划在晚上排放的冰库具有进一步降低运行成本的潜力。相比之下，当需求相对较低时，冰库在所有价格最高的时段都会正常放电，并且在其他时段（例如图4所示的第十四时段）仍有多余的储存能量可用于供应冷却负载。在这种情况下，具有适当Tao_t0_C值的鲁棒方法优于确定性方法。

        从表2可以看出，在25%和50%的设计负荷的情况下，鲁棒调度和MPC的解的平均值基本相同，而前者的值将在相对较小的范围内变化。当需求增加到设计负荷的75%时，MPC方法的平均成本相对较低，但标准偏差较大。对于设计冷负荷，MPC在平均值和标准偏差方面都优于稳健调度。MPC滚动以控制建筑能源系统，这意味着它可以适当地调整调度以满足实际负载。这就是为什么该方法可以降低操作成本，特别是当负载高时。尽管在75%和100%的设计负载的情况下，鲁棒调度引入了相对较高的平均成本，但该策略只需要在展望期之前实施一次，此外，冷却操作成本通常具有较小的标准偏差。同时，建筑能源系统的实际负荷需求大多低于设计负荷。考虑到这些优势和条件，鲁棒调度具有在实际项目中应用的潜力。

        对于RRS策略，由于前瞻期的缩短，Tao_t0_C的值；Tao_t0_PV和Tao_t0_E需要每小时修订一次。在这里，我们简单地给它们给定情况下剩余前瞻期数的一半的值。显然，RRS策略的解与MPC的解接近，而前者在大多数情况下具有较小的标准差。

4.3. Sensitivity analysis of delta_u_t_C

        不确定性水平也影响鲁棒调度的性能。表3显示了Tao_t0_PV、Tao_t0_E、Tao_t0_C分别取5、8和12的值时，不同不确定性偏差和负荷需求下的平均运营成本。显然，偏差较大的不确定冷负荷通常会增加系统运行成本，尤其是在考虑25%、50%和100%的设计负荷时。

        原因是，如果考虑较大的偏差，鲁棒调度将优化冷却器和冰库，以在最坏的情况下满足更高的负荷需求，这对建筑能源系统来说是不必要的。注意到冷水机组可以快速启动以冷却负载，我们可以选择较小的“折扣”来实现鲁棒调度，这也可以被视为调整鲁棒解决方案保守性水平的一种手段。在实际负载大于最坏情况下的负载的情况下，实时运行策略能够通过适当调整鲁棒调度来提供负载。

5. Conclusion

        在本文中，我们开发了一种鲁棒调度策略，用于具有太阳能发电系统、多机组和冰蓄能的建筑能源系统的最优监控，以应对负载和太阳能预测的不确定性。该方法采用两阶段鲁棒方法对系统运行进行优化，其中解决方案对预测误差的保守性水平可以通过“不确定性预算”来调整。利用C&CG算法，第一阶段是确定冷水机组的开/关模式和冰库的充/排模式，第二阶段是在最坏情况下优化冷水机组的输出和冰库充/排的冷却能量。最后，在一个实际的建筑能源系统中验证了该方法的有效性和性能。

        数值计算结果表明，在大多数冷负荷需求情况下，与确定性优化方案相比，具有适当Tao_t0_C值的鲁棒优化方案可使能源系统的平均运行成本较低，且标准差较小。鲁棒调度虽然只对系统运行进行了一次优化，但其最优结果与经济MPC的最优结果接近，即使在最高负荷情况下，其相对偏差也小于2%。当负荷需求较低时，鲁棒调度的运行成本变化范围较小。此外，对于包含快速启动制冷机的建筑能源系统，建议考虑相对较小的不确定性偏差进行冷负荷预测。另一种解决方案是在实际操作中利用最新的预测对鲁棒调度进行重新优化。

        进一步的研究将根据不同的部分负荷比对制冷机的COPs进行建模，并评估鲁棒调度方法在具有不同电力储存和高可再生能源渗透率的建筑能源系统中的性能。