题目:

题解:
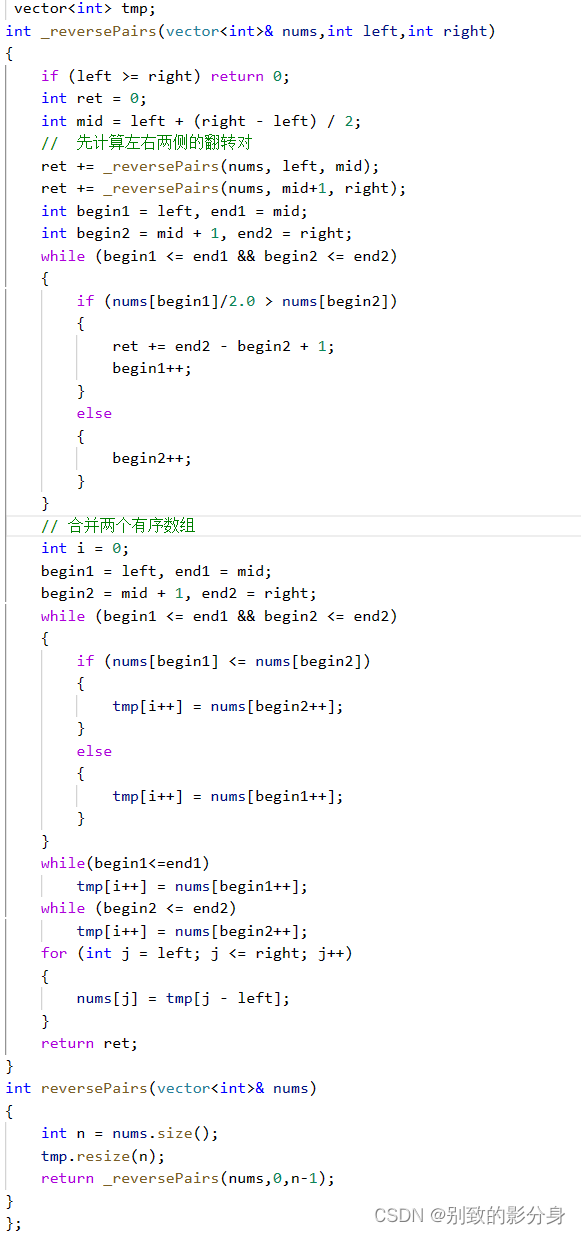
class Solution {public int lengthOfLongestSubstring(String s) {// 哈希集合,记录每个字符是否出现过Set<Character> occ = new HashSet<Character>();int n = s.length();// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动int rk = -1, ans = 0;for (int i = 0; i < n; ++i) {if (i != 0) {// 左指针向右移动一格,移除一个字符occ.remove(s.charAt(i - 1));}while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {// 不断地移动右指针occ.add(s.charAt(rk + 1));++rk;}// 第 i 到 rk 个字符是一个极长的无重复字符子串ans = Math.max(ans, rk - i + 1);}return ans;}
}