突然觉得很有必要将学过的内容记录下来，这样后续在需要用到的时候就可以避免从头进行学习，而去看自己之前做过的笔记无疑是效率更高的方法。

而作为计算机专业的学生，纸质笔记无法很好的进行记录，像写代码、画图、画表都是很麻烦的，而且纸质的很容易丢，因此还是进行电子笔记记录更佳。

那么选择用博客还是云笔记呢？私以为选择更为公开的博客，可以更加驱动自己进行详细的记录和进行浅显易懂的讲解，从而避免自己某些时候滥竽充数的行为。

原题描述

5. 最长回文子串
给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：
输入：s = “cbbd”
输出：“bb”

提示： 1 <= s.length <= 1000 s 仅由数字和英文字母组成

解答

中心移动

思想

对于这个题来说，进行最长回文子串的判断，首先想到的就是遍历所有的回文子串，然后记录最长的回文子串及其长度。
那么如何遍历这些回文子串？由于回文子串的遍历需要从中心往四周进行遍历，所以需要遍历所有的回文中心，但是回文中心会有以下两种情况。

1. 中心只有一个字符的总长度为奇数的情况，例如aba
2. 中心会有两个字符的总长度为偶数的情况，例如abba

设i, j为中心点。那么对于中心只有一个字符的情况1来说，i=j；对于中心会有两个字符的情况2来说，j=i+1。

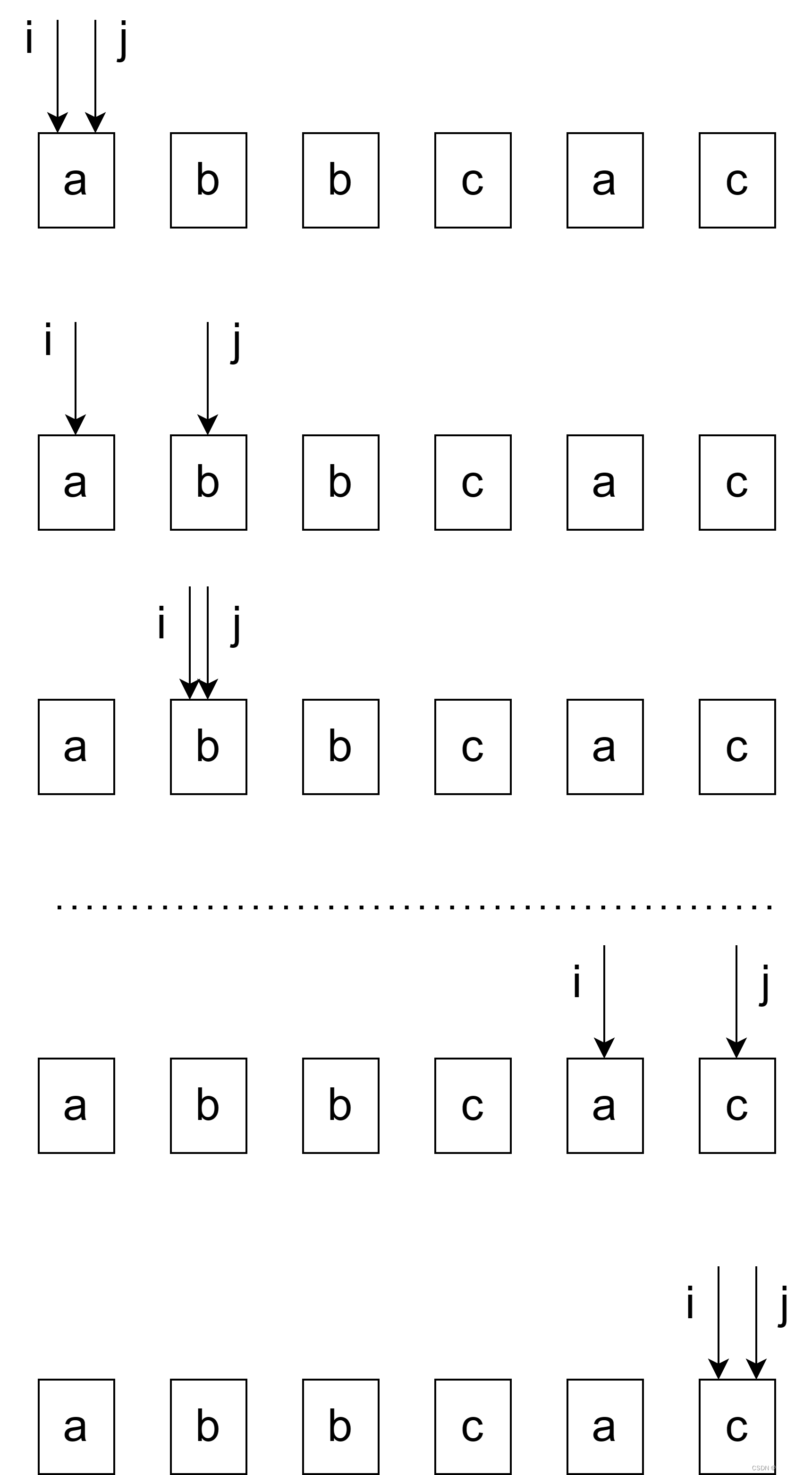
那其实就很简单了，让i、j进行这种遍历，在遍历的时候分别设置两个指针l和r进行左右的拓展，如果是回文子串就记录，否则在当下的回文中心下已经不可能有更长的回文了，进行下一次的回文中心遍历即可。

代码实现

class Solution {
public:string longestPalindrome(string s) {int len = s.length();if(len < 2)  // 特殊情况处理return s;int i=0, j=1;int maxLen = 1, startPos = 0;while(i<len-1 && j<len){if(s[i] == s[j]){int left = i-1, right = j+1;while(left>=0 && right<=len-1 && s[left]==s[right]){left--;right++;}if(right-left-1>maxLen){maxLen = right-left-1;startPos = left+1;}}if(i!=j)i++;elsej++;}return s.substr(startPos, maxLen);}
};

这里在进行实现的时候，有进行一些小tips优化：

1. i从0开始到len-2，j从1开始到len-1，也就是省略了i=0,j=0和i=len-1,j=len-1的情况。
   因为这两种情况其实也只能判断一个长度为1的回文子串，这种情况在中间的时候随便都能判断出来。最极端情况下，例如ab这样长度为2的非回文串，由于startPos和maxLen的设置，最后返回的也是a，不会出问题。
2. 中途对最长的回文子串进行记录的时候，不要直接进行截断来存字符串，而是记录开始的下标和长度，这样最后只截取一次，避免性能开销。

复杂度分析

时间复杂度

令字符串长度为n，中心只有一个字符的有n种情况，中心有两个字符的有n-1种情况。总共有2n-1种中心情况。
对于每次的中心情况进行遍历的时候，由于是向两边扩展，最多不超过n/2。
相乘，也就是O(n^2)的时间复杂度。

空间复杂度

没有开辟额外空间，O(1)

动态规划

动态规划说实话，在这个题目并不合适，还不如上面的中心移动的方法。因为动态规划相比来说会有额外的二维数组的空间开销。

思想

用最经典的动态规划思考方式来进行。设置一个二维数组dp[n][n]，其中dp[i][j]代表s[i...j]是不是回文子串，是的话为true，不是为false。

1. 最优子结构
   s[i...j]是不是回文子串，取决于s[i+1...j-1]是不是回文子串和s[i]是否与s[j]相同。
2. 状态转移方程

$$dp[i][j]==\{\begin{array}{ll}dp[i+1][j-1],& s[i]==s[j]\\ false,& s[i]!=s[j]\end{array}$$

3. 边界处理
   当i=j的时候，长度为1，必定是回文子串，dp[i][j]=true

代码实现

class Solution {
public:string longestPalindrome(string s) {int len = s.length();// 特殊处理if(len < 2)return s;int maxLen = 1, begin = 0;vector<vector<bool>> dp(len, vector<bool>(len, false));for(int i=0; i<len; i++)dp[i][i] = true;for(int j=1; j<len; j++){for(int i=0; i<j; i++){ // 注意i从0开始if(s[i] != s[j])dp[i][j] = false;else{if(j-i < 3)dp[i][j] = true;elsedp[i][j] = dp[i+1][j-1];}if(dp[i][j] == true && j-i+1>maxLen){begin = i;maxLen = j-i+1;}}}return s.substr(begin, maxLen);}
};

tips:
当s[i] == s[j]的时候，先进行了j-i<3的判断，这种情况是子串的长度<=3的情况，在这种情况下s[i]=s[j]，不管长度为2还是3，都是回文子串，直接返回true。

复杂度分析

时间复杂度

O(n^2)

空间复杂度

开辟了一个二维数组，O(n^2)

2024/03/31：
希望后面在刷算法题的时候能够坚持下来，在搞懂一个算法题之后通过博客的方式来做笔记，这样后面在warmup的时候很快就能上手，避免重复的0到1的思考。